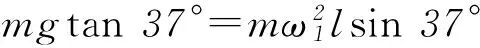微元法在高中物理解题中的应用
2016-09-28江苏姚成龙
◇ 江苏 姚成龙
◇ 山东 孙 飞
微元法在高中物理解题中的应用
◇江苏姚成龙
在一个物理过程中有一个变化的物理量,这样可能会给我们的做题带来不便,这时可以试着把这个物理过程分割为无数多个很小的过程,即所谓的微元.在每一个很小的过程中这个变化的物理量近似是不变的,然后在每一小段中求出这个物理量对时间或位移等的积累,再对这些积累量进行求和就可以得到这个物理量在整个过程中对时间或位移等的积累,这就是微元法.实际上也就是高等数学中的微积分的思想的应用.高中物理中很多习题看似“山穷水尽疑无路”,但如果用微元法的思想来分析就会“柳暗花明又一村”.实际上高中物理中根据v-t图象与坐标轴的面积求位移的方法就是微元法.
1 电磁感应中的微元法



图1
(1) 如图1所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中.金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.磁场的磁感应强度为B.请根据法拉第电磁感应定律,证明金属棒MN中的感应电动势E=Blv.

图2
(2) 为进一步研究导体做切割磁感线运动的过程,现构建如下情景: 金属棒a和b, 2棒质量都为m,电阻分别为Ra和Rb,如图2所示,a棒从h高处自静止沿弧形轨道下滑,2导轨间距为L,通过C点进入轨道的水平部分,该水平部分存在竖直向下的匀强磁场,磁感应强度大小为B.(下滑时棒始终保持与导轨垂直)
(ⅰ) 若金属棒b固定于轨道的水平部分,且a棒始终没有跟b棒相碰,求a棒上最终产生的焦耳热(不计一切摩擦).
(ⅱ) 若金属棒b解除固定,静止于轨道水平部分,要使ab不相碰,b棒至少距离C点多远.

图3




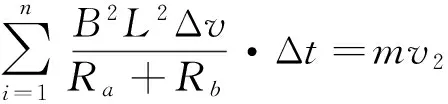
即



2 运动中的微元法
在一个运动过程中,物体在某方向上的速度在时间上的积累就是这个方向上的位移,如果在这个方向上物体做变速运动,那么我们就可以运用微元法来求解位移.
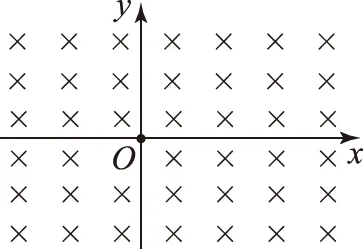
图4

(1) 若匀强电场方向水平向左,使小球在空间中做直线运动,求小球在空间中做直线运动的速度大小和方向;
(2) 若匀强电场在xOy平面内的任意方向,确定小球在xOy平面内做直线运动的速度大小的范围;
(3) 若匀强电场方向竖直向下,将小球从O点由静止释放,求小球运动过程中距x轴的最大距离.

图5

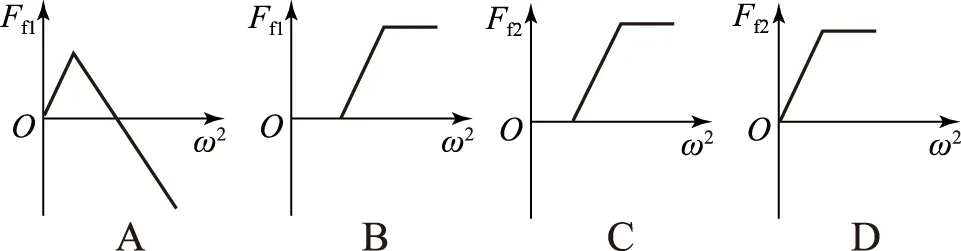
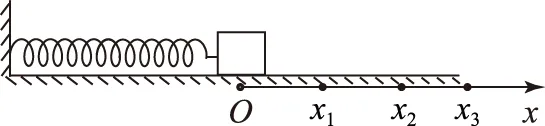
(2) 小球做直线运动的条件为洛仑兹力与电场力和重力的合力为一对平衡力.当电场在xOy平面内方向任意时,电场力与重力合力最大值为2mg,最小值为0,则BQvmax=2mg,BQvmin=0,得0 (3) 设小球运动到最低位置时下落高度为H,此时速度最大为v0,方向水平,任意时刻v沿x轴正向、y轴负向的分速度分别为vx、vy,与vy对应的洛仑兹力水平分力方向沿x轴正向,F洛x=BQvy,小球由静止释放到最低点的过程中,应用动量定理得 BQH=mv0-0. 教材中讲解了由v-t图象求位移的方法——面积法,由面积法的推导过程我们可以看出,这实际上就是运用的微元法思想.我们还可以延伸一下,用面积法根据F-t图象求冲量,根据F-x图象求功等.这种方法在高考中也多有涉及. 图6 (1) 请画出F随x变化的示意图;并根据F-x的图象求物块沿x轴从O点运动到位置x的过程中弹力所做的功. (2) 物块由x1向右运动到x3,然后由x3返回到x2,在这个过程中,(ⅰ) 求弹力所做的功,并据此求弹性势能的变化量; (ⅱ) 求滑动摩擦力所做的功,并与弹力做功比较,说明为什么不存在与摩擦力对应的“摩擦力势能”的概念. 图7 (ⅱ) 在此过程中摩擦力做功由Ff=μFN,Wf=-Ffs,得Wf=-μmg(2x3-x2-x1).因为摩擦力做功与路程成正比,而非像弹簧弹力做功一样与路径无关,而只与初末位置有关,所以无“摩擦势能”的概念. 微元法由于用到了微积分的思想,比较新颖,能够引导学生对已知物理规律的再思考,从而起到巩固知识、加深认识和提高能力的作用,同时也是近年来高考中经常涉及的方法,希望引起同学们的重视. 模型绳模型杆模型实例球与绳连接、水流星、翻滚过山车等球与杆连接、球过竖直的圆形管道,套在圆环上的物体等图示在最高点受力重力、弹力F弹向下或等于0,即mg+F弹=mv2/R重力,弹力F弹向下、向上或等于0,即mg±F弹=mv2/R恰好过最高点F弹=0,mg=mv2/R,v=Rg,即在最高点速度不能为0v=0,mg=F弹,在最高点速度可为0 1) 向心力一定指向圆心,而只有做匀速圆周运动的物体的合力才始终指向圆心. 图1 A小球A的合力小于小球B的合力; B小球A与框架间可能没有摩擦力; C小球B与框架间可能没有摩擦力; D圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大 由于合力提供向心力,依据向心力表达式F=mrω2,已知2球质量、运动半径和角速度都相同,可知向心力相同,即合力相同,故选项A错误.小球A受到重力和弹力的合力不可能垂直指向OO′轴,故一定存在摩擦力,而B球的重力和弹力的合力可能垂直指向OO′轴,故B球摩擦力可能为0,故选项B错误,选项C正确.由于不知道B是否受到摩擦力,故而无法判定圆形框架以更大的角速度转动时,小球B受到的摩擦力的变化情况,故选项D错误. 图2 (1) 若要小球离开锥面,则小球的角速度ω0至少为多大? (2) 若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大? FTcosθ=mg,FTsinθ=mω2·lsinθ. 图3 (1)若要小球刚好离开锥面,则小球受到重力和细线拉力如图3所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平. 图4 A小球的质量为aR/b; B当地的重力加速度大小为R/b; Cv2=c时,在最高点杆对小球弹力方向向上; D若v2=2b,则在最高点杆对小球弹力大小为2a 4.1圆周运动的临界极值问题 (1) 若装置匀速转动的角速度为ω1时,细线AB上的张力为0,而细线AC与竖直方向的夹角仍为37°,求角速度ω1的大小; (2) 若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为0,求此时角速度ω2的大小; (3) 装置可以以不同的角速度匀速转动,试通过计算,在图6的坐标中画出细线AC上张力FT随角速度的平方ω2变化的关系图象. 图5 图6 FTcosθ=mg,FT=mg/cosθ=12.5 N. ω1≤ω≤ω2时细线AB松弛, 细线AC上张力的水平分量等于小球做圆周运动需要的向心力 FTsinα=mω2lsinα,FT=mω2l.ω>ω2时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力,则 FTsinθ′=mω2lsinθ′, 图7 即 FT=mω2l. 4.2圆周运动中的连接体问题 图8 4.3圆周运动的多过程问题 图9 A2钉子间的距离为绳长的1/6; Bt=10.5 s时细绳拉力的大小为6 N; Ct=14 s时细绳拉力的大小为10 N; D细绳第3次碰钉子到第4次碰钉子的时间间隔为3 s (作者单位:山东省枣庄市台儿庄区职业中专) 江苏省江阴市山观高级中学) ◇山东孙飞3 微元法的变形——面积法



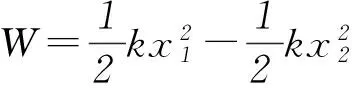
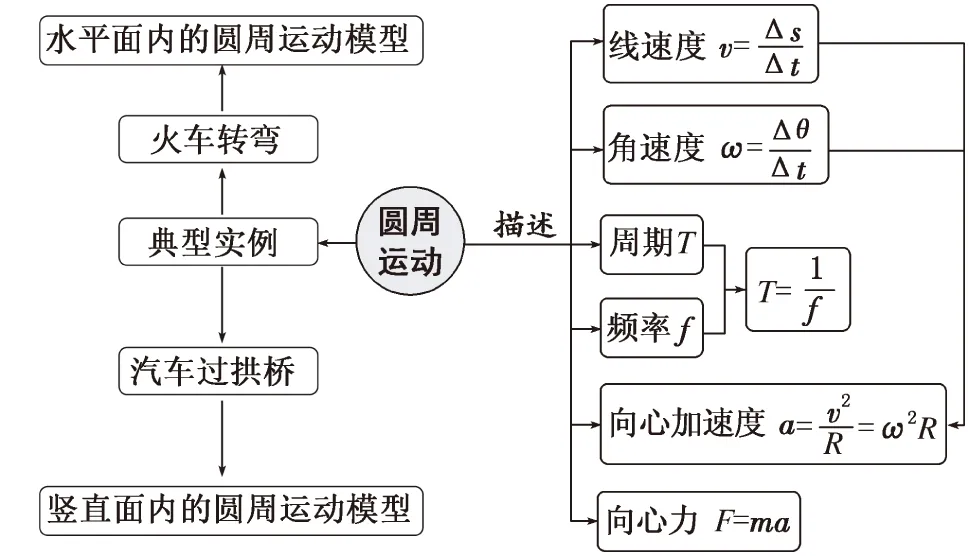
1 构建1个知识网络——解题的知识依托
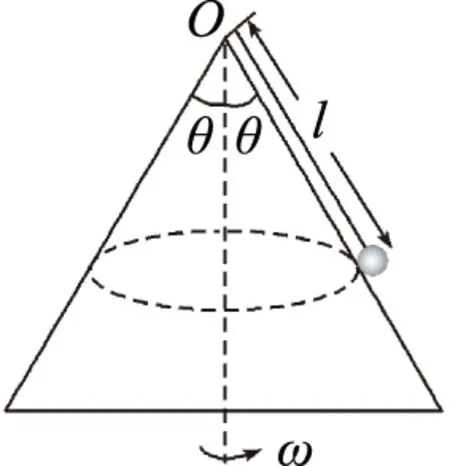
2 内化2种模型——化繁为简的有效途径

3 铭记2个特点——这是快速解题的切入点







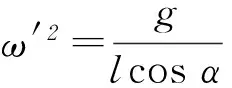
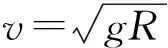



4 突破3个题型