三维不可压Euler方程的动力学

李 丹，邓大文

（湘潭大学 数学与计算科学学院，湖南 湘潭 411105）

三维不可压Euler方程的动力学

李 丹，邓大文

（湘潭大学 数学与计算科学学院，湖南 湘潭 411105）

考虑三维不可压Euler方程的一些物理量沿质点轨迹的演化情况。Chae已考虑了涡量沿质点轨迹增加的情景，文章考虑令解衰减、系统稳定的另一种情景，进而把系统的演化情况（包括它在两种情景间的转化、爆破或衰减）作完整的描述。推广了Chae已考虑的情景的结果，得到更强的结论。

三维不可压Euler方程；局部光滑解；爆破；渐近性质

本文考虑在Ω⊂R3中不可压流体的Euler方程

三维Euler方程局部光滑解可否在有限时间内损失正则性，是受关注的问题。如果可以，其爆破形态也是研究的中心问题。这方面的研究有文献［1-3］中的爆破条件。Chae［4］考虑Euler方程组在光滑解存在的时段内的一些相关量沿质点轨迹的演化情况，思路是在光滑解全局存在的假定下，推出矛盾，就可知道全局光滑解不存在。

Guo等［5］利用Euler方程和水波的逼近模型Camassa-Holm（CH）方程的相似性，对CH方程（事实上也对Degasperi-Procesi方程）得到类似于文献［4］的结果。但因为CH方程是空间一维的，涉及的量较简单，结果就更清楚明白。更重要的是对CH方程有较完整的全局光滑解存在性和局部光滑解在有限时间爆破的理论［6-8］。利用这些理论，文献［5］得到CH方程真实出现的全局解的性质和局部解的爆破形态，不单只是爆破条件与罗列所有可能的发展情况。也可以用类似的方法讨论SQG方程局部光滑解的爆破问题［9］。

文献［4］中的方法，是从模型推导物理量沿质点轨迹满足的常微，从而得到它们沿轨迹的演化情况。但没有考虑常微的某些令解衰减、系统稳定的初始形态。本文考虑这些形态，并推广文献［4］中已考虑的情况，得到更强的结果。对于CH方程，也可以类似地讨论未被考虑的情况，并推广文献［5］中的结果，这里不作详细讨论。

1　主要结果

以下定理讨论ω及ω相对于α沿质点轨迹的演化情况。这里对文献［4］中的定理1.1补充了初始情况α0（a）＜0的讨论，及把定理中的指数γ=1推广到γ＞0，得到比文献［4］中更强的结论。若ω（X（a，t），t）一直小于1（大于1），则对γ＞1（γ＜1），模糊递减的结论比文献［4］中得更快。从式（2）可知，若ω0（a）≠0，则ω（X（a，t），t）≠0。当ω（X（a，t），t）=0，定义α（X（a，t），t）=ρ（X（a，t），t）=0。

定理1令v0∈Hs（Ω），且 γ＞0。定义

则以下结论成立。

（Ⅰ）当a∈Σ+1（0），以下情况有且只有一种成立：

（a）ω（X（a，t），t）在有限时间内沿着轨迹的结论更强，即α衰减

｛X（a，t）｝爆破，即存在T∗＞0，使得

当 j→∞时，t1＜t2＜…＜tj＜tj+1→∞，使得对所有 j=1，2，3，…，有Φ1（a，0）＜Φ1（a，t1）＜…＜Φ1（a，tj）＜Φ1（a，tj+1）＜0，且对t∈［0，tj］，有Φ1（a，t）≤Φ1（a，tj）＜0。

以下的定理对应于文献［4］中的定理1.2，这里补充了两种初始情况的讨论，及把文献［4］中定理1.2的指数γ=1推广到γ＞0。由式（2）可得［4］561

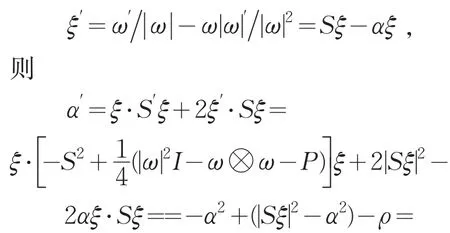
以下 Φ2对应于文献［4］中定理1.2的Φ2-1。

定理2令 v0∈Hs（Ω），s＞5/2，γ＞0，当α（X（a，t），t）≠0，定义

则以下结论成立：

（a）Euler方程的解v在有限时间内沿着轨迹｛X（a，t）｝爆破。

（c）存在 T1＞0，使得 Φ2（a，T1）=0，或者（Φ2“模糊地单调”存在一个无穷序列，当 j→∞时，t1＜t2＜…＜tj＜tj+1→∞，使得

Φ2（a，tj）＞Φ2（a，tj+1）＞0，且对t∈［0，tj］，有Φ2（a，t）≥Φ2（a，tj）＞0。

Φ2（a，tj+1）＜0，且对t∈［0，tj］，有Φ2（a，t）≤Φ2（a，tj）＜0。

（b）存在 T1＞0，使得 Φ2（a，T1）=0。

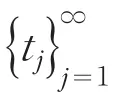
由式（3）及Φ2的定义得，α′=Φ2|α|1+γ。在情景（Ⅰ）中，不管α（X（a，t），t）属于还是， |α（X（a，t），t）|都递增，可能爆破；在情景（Ⅱ）中，无论α（X（a，t），t）属于（t）还是，|α（X（a，t），t）|都递减。若（Ⅰ）（b）发生，α可能变号，或当（Ⅰ）（c）中的Φ2（a，t）=0发生，Φ2可能变号，任何一种都可令系统从情景（Ⅰ）进入情景（Ⅱ）；类似地，若（Ⅱ）（a）或（Ⅱ）（b）发生，系统也可能从情景（Ⅱ）变到情景（Ⅰ）。所以沿某质点轨迹，系统可以在情景（Ⅰ）（Ⅱ）间往返，若在某时间后逗留在（Ⅰ）中，则||α沿轨迹增加且可能爆破；若逗留在（Ⅱ）中，则||α衰减。

2　定理的证明

定理1的证明需要以下的引理。

引理1假设α0（a）＞0， ω0（a）≠0，γ＞0且存在ε＞0，使得α0（a）|ω0（a）|≥ε|ω0（a）|1+γ。

令T*=［εγ|ω0（a）|γ］-1，那么ω（X（a，t），t）不晚于T*爆破，或者存在t∈（0，T*），使得

证明：假设ω（X（a，t），t）不在［0，T*］内爆破，且对t∈（0，T*），有

定理1的证明：由式（2）可得

因此从ω0（a）≠0推出ω（X（a，t），t）≠0。

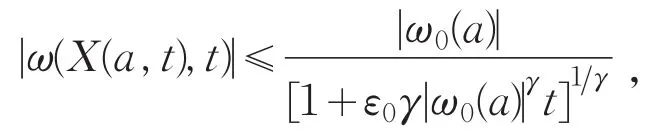
所以对t*=0，（Ⅱ）（b）成立；否则存在 t1＞0，使α（X（a，t1），t1）|ω（X（a，t1），t1）|＞-ε0|ω（X（a，t1），t1）|1+γ，则

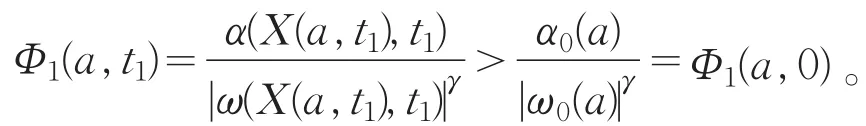
α（X（a，t），t）|ω（X（a，t），t）|≤-ε1|ω（X（a，t），t）|1+γ，则

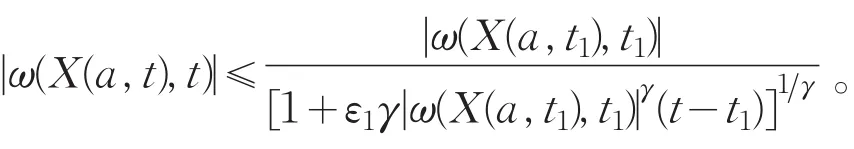
所以对t*=t1，（Ⅱ）（b）成立；否则存在t2＞t1，使

则

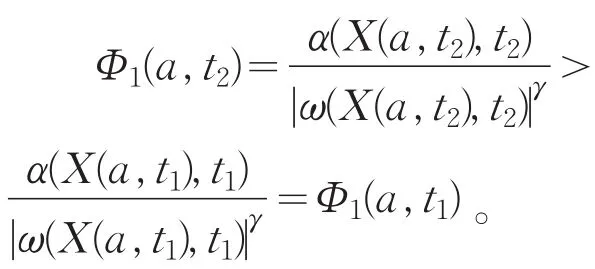
重复上面的讨论，若（Ⅱ）（b）永远不成立，可得到一个无穷序列，t1＜t2＜…＜tj＜tj+1，使对j=1，2，…，有Φ1（a，tj）＜Φ1（a，tj+1）＜0。选择每个tj使得对任意的t∈［0，tj］有Φ1（a，t）≤Φ1（a，tj）；否则，重选tj为Φ1（a，t）在（tj-1，tj］上的最大值即可。

若当 j→∞，tj→t∞＜∞，可重选t∞为，原来的…都丢掉，可得到当 j→∞，有tj→∞。

为证明定理2，先证明以下两个引理。

引理2假设α0（a）＞0，γ＞0且Φ2（a，0）＞0。

证明：假设解 v不在［0，T*］内爆破，且对t∈（0，T*），Φ2（a，t）≥Φ2（a，0），连同式（3）得，当t∈（0，T*）时，α′=Φ2（a，t）|α|1+γ≥Φ2（a，0）|α|1+γ，因Φ2（a，0）＞0，所以α′＞0。又因α0（a）＞0，则当t∈（0，T*）时，α＞0。因此α′≥Φ2（a，0）α1+γ，从而

引理3假设α0（a）＜0，γ＞0且Φ2（a，0）＜0。令T*=［-Φ2（a，0）γ（-α0（a）γ］-1。那么，解v不晚于T*爆破，或者存在t∈（0，T*），使得

Φ2（a，t）＞Φ2（a，0）。

证明：假设解v不在［0，T*］内爆破，且对t∈（0，T*），Φ2（a，t）≤Φ2（a，0），由式（3）得，当t∈（0，T*）时，α′=Φ2（a，t）|α|1+γ≤Φ2（a，0）|α|1+γ，因Φ2（a，0）＜0，所以α′＜0。又因α0（a）＜0，则当t∈（0，T*）时，α＜0。因此α′≤Φ2（a，0）（-α）1+γ，从而

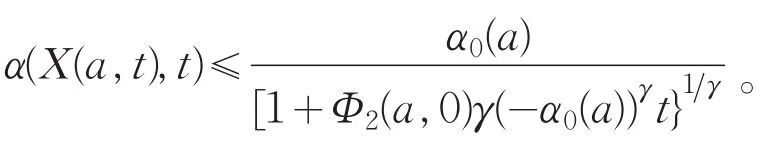
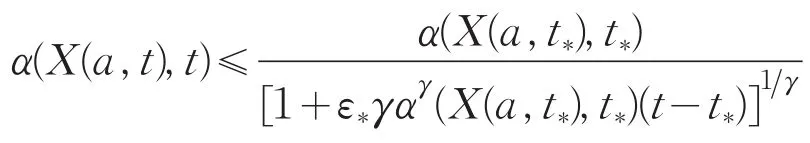
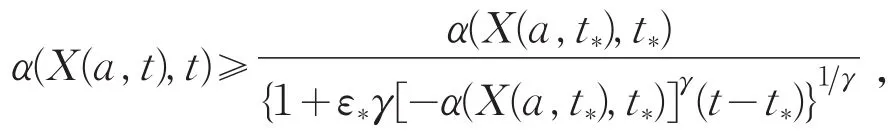
即（Ⅱ）（c.2）成立。否则，对所有ε＞0，T＞0，存在t＞T，使Φ2（a，t）＜ε。令ε0=Φ2（a，0），则存在t1＞0，使Φ2（a，t1）＜ε0=Φ2（a，0）。令ε1=Φ2（a，t1），则存在 t2＞t1，使 Φ2（a，t2）＜ε1=Φ2（a，t1）。类似的讨论，得（Ⅱ）（d.2）成立。

［1］BEALE J T，KATO T，MAJDA A.Remarks on the breakdown of smooth solutions for the 3-D Euler equations［J］. Communications in Mathematical Physics，1984，94（1）：61-66.

［2］PONCE G.Remarks on a paper by J.T.Beale，T.Kato and A.Majda［J］.CommunicationsinMathematicalPhysics，1985，98（3）：349-353.

［3］CONSTANTIN P，FEFFERMAN C，MAJDAA J.Geometric constraints on potentially singular solutions for the 3-D Euler equations［J］.Communications in Partial Differential Equations，1996，21（3-4）：559-571.

［4］CHAE D.On the lagrangian dynamics for the 3D incompressible euler equations［J］.Communications in Mathematical Physics，2007，269（2）：557-569.

［5］GUO W W，TANG T M.Evolutions of the momentum density，deformation tensor and the nonlocal term of the Camassa-Holm equation［J］.Nonlinear Analysis，2013，88（9）：16-23.

［6］CONSTANTIN A.Existence of permanent and breaking waves for a shallow water equation:A geometric approach ［J］.Annales De Linstitut Fourier，2000，50（2）：321-362.

［7］RODRIGUEZ-BLANCO G.On the Cauchy problem for the Camassa-Holm equation［J］.Nonlinear Analysis Theory Methods&Applications，2001，46（3）：309-327.

［8］LAI S，WU Y.Global solutions and blow-up phenomena to a shallow water equation［J］.Journal of Differential Equations，2010，249（3）：693-706.

［9］CHAE D，CONSTANTIN P，WU J.Deformation and symmetry in the inviscid SQG and the 3D Euler equations［J］.Journal of Nonlinear Science，2012，22（5）：665-688.

［10］MAJDA A J，BERTOZZI A.Vorticity and ncompressible low［M］.Cambridge：Cambridge University Press，2002：170.

Dynamics of the 3D Incompressible Euler Equation

LI Dan，TANG Taiman（邓大文）
（School of Mathematics and Computational Science，Xiangtan University，Xiangtan 411105，Hunan，China）

A study is made of the evolutions along particle trajectories of some physical quantities of the three dimensional incompressible Euler equation.In the literature，Chae has considered the scenario in which the magnitude of the vorticity increases along particle trajectories.In this article，a discussion is made of another scenario which results in decaying solutions and stable systems.Consequently，a complete description of the evolution of the Euler system can be given，including the changing of scenarios，blowing up and decay of the solution.Chae's results in the scenario he has considered are also generalized.

3D incompressible Euler equation；local smooth solution；blow-up；asymptotic properties

O175.24

A

1672-2914（2016）04-0033-05

2016-04-12

国家自然科学基金项目（11371300）。

李 丹（1991—），女，山西大同市人，湘潭大学数学与计算科学学院硕士研究生，研究方向为偏微分方程。

邓大文，教授，E-mail:tmtang@xtu.edu.cn。