基于奇系数Comb的椭圆曲线密码抗功耗攻击方案
2016-09-26沈济南
梁 芳 沈济南,2
1(湖北民族学院理学院 湖北 恩施 445000)2(华中科技大学计算机科学与技术学院 湖北 武汉 430074)
基于奇系数Comb的椭圆曲线密码抗功耗攻击方案
梁芳1沈济南1,2
1(湖北民族学院理学院湖北 恩施 445000)2(华中科技大学计算机科学与技术学院湖北 武汉 430074)
针对资源受限的密码芯片在抵抗功耗攻击中存在效率和安全两个方面的矛盾。通过将标量采用奇系数梳状算法进行编码,然后结合预计算表将椭圆曲线标量乘法运算转化为一组小标量乘法运算,并利用基点掩码技术实施抗功耗攻击,提出一种基于奇系数Comb的椭圆曲线密码抗功耗攻击方案。算法性能分析结果表明:与传统的抗功耗攻击方案相比,给出的抗功耗攻击方案不仅可以抵抗简单功耗攻击、差分功耗攻击、零值寄存器功耗攻击和零值点功耗攻击,并且能够在存储空间和主循环运算量基本保持不变的情况下具有更高效的运算效率,在各种资源受限的应用系统中具有较好的实际应用价值。
椭圆曲线密码功耗攻击奇系数梳状算法预计算表基点掩码
0 引 言
密码芯片由于资源受限,使得其在实施抗功耗攻击过程中存在效率和安全的矛盾,尤其是功耗攻击技术的出现对密码芯片的安全造成了严重威胁。功耗攻击技术是1998年由PaulKocher率先提出的一种利用芯片工作时泄露的功耗信息来获取密钥信息的密码分析方法,这种攻击方法实现简单,攻击成功率高,比传统的数学攻击方法具有更大的威胁[1-4]。根据攻击手段不同,可分为简单功耗分析SPA(SimplePowerAttack)和差分功耗分析DPA(DifferentialPowerAttack)。由于椭圆曲线密码算法ECC(EllipticCurveCryptogram)与其他的传统公钥密码算法相比,在相同安全性条件下具有所需要的密钥更短,存储空间更小的优点,更适合于密码芯片等资源受限的设备,所以目前出现了大量针对椭圆曲线密码的功耗攻击,主要有零值寄存器功耗分析ZPA(Zero-valuePowerAnalysis)和零值点功耗分析RPA(RefinedPowerAnalysis)[5-7]。
同时,国内外文献也出现了针对椭圆曲线密码的抗功耗攻击分析研究。文献[8]提出了一种基于窗口随机化初始点WBRIP(Window-BasedRandomInitialPoint)的椭圆曲线密码抗功耗攻击算法,其主要思想是通过将椭圆曲线密码标量的二进制编码进行窗口化,从而掩盖在一个窗口内执行点加操作和倍点操作运算的次数,使得攻击者无法根据中间结果猜测运算过程中执行的具体操作,该算法虽然能够抵抗多种功耗攻击,但在运算效率方面需要进一步改进。文献[9]对上述算法进行改进,给出了一种固定窗口宽度为w的非邻接形式表示算法FWNAF(FractionalWidth-wNonAdjacentFrom)的椭圆曲线密码抗功耗攻击方案,通过优化编码减少添加伪操作次数,以提高改进方案的运算效率。文献[10]提出了一种高效的窗口随机化初始点EBRIP(Efficient-BasedRandomInitialPoint)椭圆曲线密码抗功耗攻击算法,通过将窗口宽度为w的非邻接表示形式分成整数部分和分数部分实现抗SPA攻击,然后将基点分成固定部分和可变部分实现DPA、ZPA和RPA攻击,并且可以有效提高运算效率。奇系数梳状算法是椭圆曲线标量乘法运算的一种快速计算方法,通过将添加伪操作和基点掩码技术应用在奇系数梳状算法中,给出一种基于奇系数Comb算法OCM(Odd-onlyCombMethod)的椭圆曲线密码抗功耗攻击方案,与WBRIP和EBRIP算法比较,给出的抗功耗攻击算法具有相同的抗功耗安全性,且有更高的运算效率。
1 椭圆曲线标量乘快速算法
椭圆曲线密码的标量乘快速算法主要有双基数系统编码算法[11]、阶乘展开式编码算法[12]和整数拆分表示形式编码算法[13]等。奇系数梳状算法是常用的椭圆曲线标量乘快速算法,与其他快速算法相比具有存储空间小和运算效率高的优点。下面给出椭圆曲线标量乘奇系数梳状快速算法的具体描述。
首先,给出椭圆曲线密码的标量乘法运算如式(1)所示:
(1)
其中,标量k采用二进制编码,n为编码长度,ki为编码系数。
通过对椭圆曲线密码的正奇数标量采用奇系数梳状算法进行重新编码,则有椭圆曲线密码标量的奇系数梳状形式编码如式(2)所示:
(2)
(3)
其中,Pi为预计算点,通过预计算可以构造出预计算表,且有Pi=(u(s-1)2(s-1)t+…+ui2it+…+u12t+1)·P,且ui∈{0,1}。
将所给已知标量进行奇数化,即如果标量k是正奇数,则有l=k+1;然而如果标量k是正偶数,则有l=k+2。因为对原标量k进行了奇数化,所以在返回结果Q时需要增加一次后处理:如果标量k是奇数,则需增加操作Q=Q-2P;如果标量k是偶数,则需增加操作Q=Q-P。则如果椭圆曲线密码标量经过重新编码后,奇系数梳状标量乘法运算如算法1所示[14]:
算法1奇系数梳状椭圆曲线密码标量乘快速算法
输入:l,s,P;
输出:Q=lP。
1. 令m为奇数化标量l的二进制比特长度;
2. 构造预计算表Pi;
4. 计算奇系数梳状编码系数li;
5. 令Q=O;
6. 对于i从t-1到0,重复执行:
6.1Q=2Q;
6.2Q=Q+liP;
7. 返回输出值:
7.1 如果k是偶数,则返回Q=Q-P;
7.2 如果k是奇数,则返回Q=Q-2P。
2 基于OCM的抗功耗攻击方案
算法1中,由于奇系数编码系数li均不为0,所以在执行步骤6的过程中,总是执行相同的操作顺序,即每执行一次倍点操作就需要执行一次点加操作,具有相同的能量图谱,没有明显的功耗差异,使得攻击者无法利用功耗差异信息猜测密钥信息,并且在步骤7中都执行了一次点加操作运算,所以也不会泄露所给已知标量的奇偶性,因此算法1可以有效抵抗SPA攻击。然而,由于基点P是已知的,使得中间结果与输入之间存在相关性,攻击者可以利用中间结果信息猜测密钥信息,而且所给已知的基点中同时也存在有特殊点被攻击者利用实施ZPA和RPA攻击,所以算法1无法抵抗DPA、ZPA和RPA攻击。
通过结合掩码技术[15],引入一个随机点,将每一个小标量乘法运算的基点进行随机化,以掩盖小标量和功耗之间的相关性,从而使得攻击者无法通过多次猜测获取密钥信息。则有引入随机点R后,基于奇系数Comb编码标量乘法运算Q=lP变换为如式(4)所示:
(4)
由于引入了一个随机点,所以在返回结果Q时,需要再增加一次后处理进行恢复:如果标量k是奇数,则需增加操作Q=Q-2P-R;如果标量k是偶数,则需增加操作Q=Q-P-R。下面给出基于奇系数梳状算法的椭圆曲线密码抗功耗攻击方案,如算法2所示:
算法2奇系数梳状椭圆曲线密码抗功耗攻击算法
输入:l,P;
输出:Q=lP。
1. 令m为奇数化标量l的二进制比特长度;
2.R=random()
5. 计算奇系数梳状编码系数li;
6. 令Q=R;
7. 对于i从t-1到0,重复执行:
7.1Q=2Q;
7.2Q=Q+liP;
8. 返回输出值:
8.1 如果k是偶数,则返回Q=Q-P-R;
8.2 如果k是奇数,则返回Q=Q-2P-R。
3 算法性能分析
算法2中,通过引入随机点R,将预计算表中的Pi进行随机化,从而可以消除中间结果与功耗之间的相关性信息,并且不会存在可以被攻击者利用的特殊点,所以给出的算法2可以抵抗DPA、ZPA和RPA攻击。同时,由于算法2没有系数为0的系数,因而不存在功耗差异操作,从而具有相同的能量消耗图谱,本身具有抵抗SPA攻击的能力。另外,算法2通过执行两次后处理操作:一方面可以掩盖原标量的奇偶性,进一步增强算法的安全性;另一方面通过减去引入的随机点,可以恢复出真实的返回值。
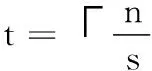
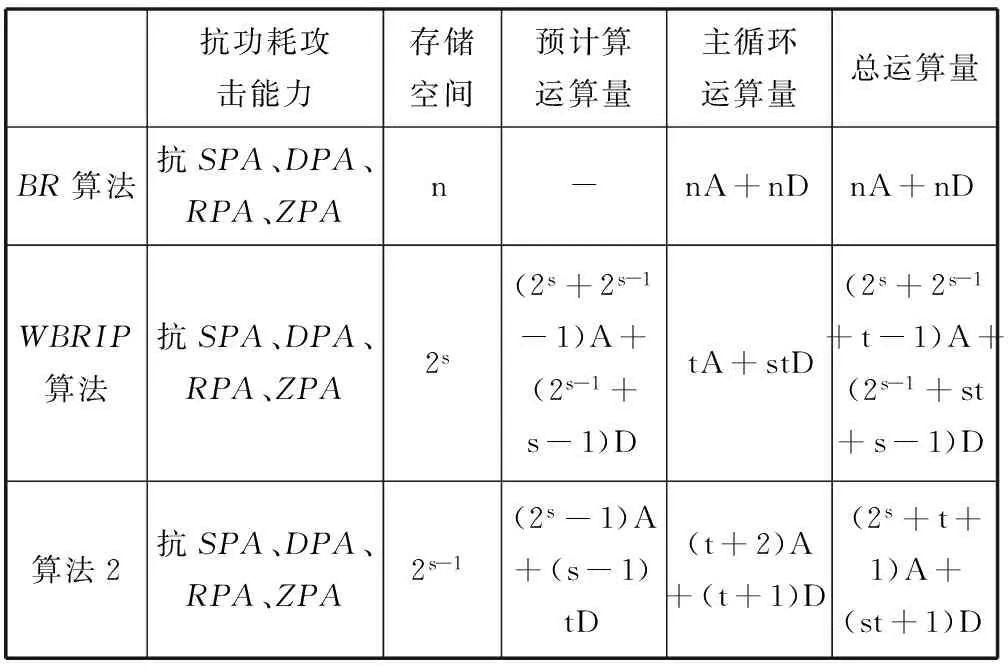
表1 算法2与BR和WBRIP抗功耗攻击算法的性能比较
从表1可以看出,所给算法2比WBRIP抗功耗攻击算法所需的存储空间小。然而,WBRIP抗功耗攻击算法比所给的算法2多执行了(2s-1-2)次点加操作运算和(2s-1+s-2)次倍点操作。所以算法2在存储空间减少的情况下,具有相同的抗功耗攻击能力,且有更高效的运算效率。目前,一般认为椭圆曲线密码512比特的密钥是安全的,即t=512。令s=4,有t=128。另外,文献[16]给出在仿射坐标系下,倍点运算D=24M,点加运算A=23M,M表示模乘运算。表2给出了算法2与BR抗功耗攻击算法和WBRIP抗功耗攻击算法的运算效率比较。
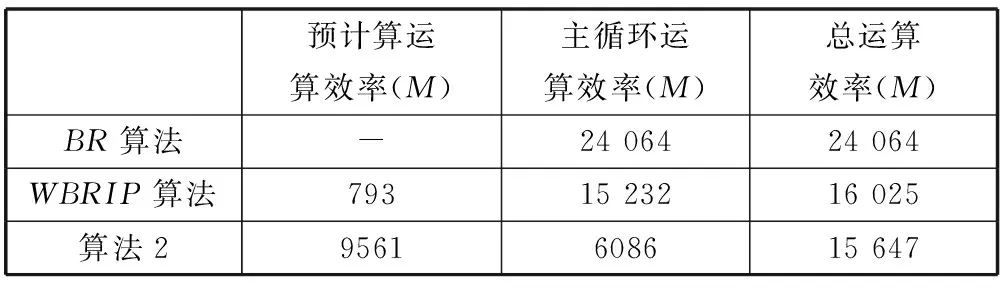
表2 算法2与BR和WBRIP抗功耗攻击算法的运算效率比较
从表2可以看出,所给算法2的总运算效率比BR抗功耗攻击算法提高34.98%,比WBRIP抗功耗攻击算法提高2.36%。其中,算法2比WBRIP抗功耗攻击算法所需预计算大的多,然而由于预计算表可以预先存储到密码芯片中,因而需要考虑主要是主循环运算,算法2的主循环运算效率比WBRIP抗功耗攻击算法的主循环运算效率提高了60.04%,比BR抗功耗攻击算法的主循环运算效率提高了74.71%,而WBRIP抗功耗攻击算法的主循环运算效率比BR抗功耗攻击算法只提高了36.70%。由此可知,所给算法2可以同时兼顾安全和效率两个方面,进一步提高密码芯片的运算效率,能够很好地满足资源受限的各类应用环境中。
4 结 语
椭圆曲线密码算法是密码安全芯片中的主流加密算法,而奇系数梳状算法是椭圆曲线密码中的一种快速标量乘算法。由于功耗攻击的出现,使得密码安全芯片的安全性受到比较大的威胁,因而通过结合奇系数梳状快速标量乘算法和基点掩码技术给出的抗功耗攻击算法,可以有效抵抗多种功耗攻击,并且同其他传统抗功耗攻击算法相比,所给算法可以进一步有效提高运算效率,很好地解决了资源受限的密码芯片效率和安全的矛盾问题。因而所给算法可以很好地应用各种资源受限的应用系统中,具有很好的理论研究意义和实际推广应用价值。
[1] 李浪,李仁发,ShaEHM.安全SoC抗功耗攻击研究综述[J].计算机科学,2009,36(6):16-18.
[2]KocherP,JaffeJ,JunB.Differentialpoweranalysis[C]//ProceedingsofAdvancesinCRYPTO99,LNCS1666,Springer-Verlag,BerlinHeidelberg,1999:388-397.
[3]WuK,LiH,YuF.Retrievinglostefficiencyofscalarmultiplicationsforresistingagainstside-channelattacks[J].Journalofcomputers,2010,5(12):1878-1884.
[4] 王正义,赵俊阁.ECC抗功率分析攻击的等功耗编码算法[J].计算机工程,2012,38(10):111-113.
[5]GoronJS.Resistanceagainstdifferentialpoweranalysisforellipticcurvecryptosystems[C]//CryptographicHardwareandEmbeddedSystems(CHES’04),LNCS1717,Springer-Verlag,Berlin,1999:292-302.
[6] 汪鹏君,郝李鹏,张跃军.防御零值功耗攻击的AESSubByte模块设计及其VLSI实现[J].电子学报,2012,40(11):2183-2187.
[7]GobinL.Arefinedpoweranalysisattackonellipticcurvecryptosystems[C]//PublicKeyCryptography2003,LNCS2567,Springer-Verlag,2003.
[8]MamiyaH,MiyajiA,MorimotoH.EfficientcountermeasuresagainstRPA,DPA,andSPA[C]//CryptographicHardwareandEmbeddedSystems(CHES’04),LNCS3156,Springer-Verlag,2004:343-356.
[9] 张涛.Smartcard上椭圆曲线密码算法的能量攻击和防御[J].计算机工程,2007,33(14):125-127.
[10]ZhangTao,FanMingyu,ZhengXiaoyu.Secureandefficientellipticcurvecryptographyresistsside-channelattacks[J].JournalofSystemsEngineeringandElectronics,2009,20(3):660-665.
[11]DimitrovVS,JullienGA,MillerWC.Theoryandapplicationsforadouble-basenumbersystem[J].IEEETransactionsonComputers,1999,48(10):1098-1106.
[12] 赖忠喜,张占军,陶东娅.椭圆曲线中直接计算7P的方法及其应用[J].计算机应用,2013,33(7):1870-1874.
[13] 石润华,葛丽娜,钟诚.椭圆曲线密码体制上一种快速kP算法[J].计算机工程与科学,2004,26(4):55-58.
[14] 蒋辉芹.标量乘法底层域快速算法研究[J].湖州师范学院学报,2013,35(3):36-40.
[15] 李起瑞,胡晓波,赵静,等.针对改进的Masking方法的差分功耗攻击[J].北京电子科技学院学报,2011,19(4):35-41.
[16] 王玉玺,张串绒,张柄虹,等.基于素数域上复合运算的快速标量乘算法[J].计算机应用研究,2013,30(11):3385-3387.
RESISTINGPOWERANALYSISATTACKSSCHEMEFORELLIPSECURVECRYPTOGRAPHYBASEDONODD-ONLYCombMETHOD
LiangFang1ShenJi’nan1,2
1(School of Science,Hubei Minzu University,Enshi 445000,Hubei,China)2(School of Computer Science and Technology,Huzhong University of Science and Technology,Wuhan 430074,Hubei,China)
Thecontradictionsbetweenefficiencyandsecurityliesinthecryptographicchipswithlimitedresourcewhenresistingpoweranalysisattacks.Inlightofthis,wecodedthescalarwiththeodd-onlycombalgorithmandthenconvertedtheellipsecurvescalarmultiplicationoperationtoagroupofsmallscalarmultiplicationoperationsincombinationwiththepre-computationtable,andutilisedthemasktechnologytoexertpoweranalysisattacksresistance,throughthesewepresentedanodd-onlyComb-basedresistingpoweranalysisattacksschemeforellipsecurvecryptography.Performanceanalysisresultofthealgorithmshowedthatcomparedwithtraditionalresistingpowerattackscheme,theproposedschemecouldresistthesimplepoweranalysisattack,thedifferentialpoweranalysisattack,thezero-valueregistermasktechnologypowerattackandthezero-valuepointpoweranalysisattack.Besides,italsohadmoreefficientoperationefficiencyinthecircumstanceofkeepingthestoragespaceandmainloopoperationloadbasicallyunchanged,andhadbetterpracticalappliedvalueinavarietyofapplicationsystemswithlimitedresource.
EllipsecurvecryptographyPoweranalysisattackOdd-onlycombalgorithmPre-computationtableBasicpointmask
2014-07-03。国家自然科学基金面上项目(612720 72)。梁芳,讲师,主研领域:云计算,数据安全,访问控制。沈济南,讲师。
TP309
ADOI:10.3969/j.issn.1000-386x.2016.03.068
