CONVERGENCE OF INVARIANT MEASURES FOR MULTIVALUED STOCHASTIC DIFFERENTIAL EQUATIONS∗

Yue GUAN（关岳）

School of Mathematics and Computational Science，Sun Yat-Sen University，Guangzhou 510275，China

E-mail∶guanyue1@yahoo.com

Hua ZHANG（张华）

School of Statistics&Research Center of Applied Statistics，

Jiangxi University of Finance and Economics，Nanchang 330013，China

E-mail∶zh860801@163.com



CONVERGENCE OF INVARIANT MEASURES FOR MULTIVALUED STOCHASTIC DIFFERENTIAL EQUATIONS∗

Yue GUAN（关岳）

School of Mathematics and Computational Science，Sun Yat-Sen University，Guangzhou 510275，China

E-mail∶guanyue1@yahoo.com

Hua ZHANG（张华）

School of Statistics&Research Center of Applied Statistics，

Jiangxi University of Finance and Economics，Nanchang 330013，China

E-mail∶zh860801@163.com

This article is concerned with the weak convergence of invariant measures associated with multivalued stochastic differential equations in the finite dimensional space.

Invariant measure；multivalued stochastic differential equation；maximal monotone operator；Yosida approximation

2010 MR Subject Classification60H15

1　Introduction

On the basis of the theory of evolution equations with maximal monotone operators（see for example［1］），［2］introduced the notion of multivalued stochastic differential equations（shortly，MSDE's）.Later，［3］showed that this notion was a generalization of the classic Skorohod problem under an essential hypothesis that the interior of the effective domain of monotone operators was non-empty.Since then，MSDE's in finite dimensional spaces were extensively studied by many authors such as［4，5］.There are also some articles on MSDE's in the infinite dimensional case，such as［6］in Hilbert spaces，and［7］under the framework of evolution triples.

In this article，we studied the weak convergence of invariant measures associated with two related MSDE's.The existence and uniqueness of invariant measures was established in［7］. Considering the Prokhorov's approach，we only need to show first the tightness，and then the uniqueness of the possible limit points.Fortunately，by the methods of［8］，we can solve the former problem.If we want to show the convergence of invariant measures，we must first show at least the convergence of the corresponding solutions in the law.This kind of convergence was studied in［9］with a gradient operator other than a multivalued one.However，in ourmore general situations，their result can not be used directly.Using a lemma of approximating stochastic integral by smoothing functions from［10］，we can show the L2convergence，and this fulfills our needs.During the proof of the latter problem，we use the e-property of our semigroups and a result of characterizing the weak convergence of measures by some metric induced by Lipschitz functions.

In the rest of this section，we give some notations and our main result.In next section，we divide our total proofs into two subsections，which show the tightness of all invariant measures and the uniqueness of possible limit points，respectively.

A set A⊂Rd×Rdcan be viewed as a multivalued operator from Rdto Rdin the sense that Ax：=｛y∈Rd：［x，y］∈A｝，x∈D（A）：=｛x∈Rd：Ax 6=∅｝.The operator A is called monotone if〈x1−x2，y1−y2〉≥0，for all［x1，y1］，［x2，y2］∈A.The operator A is called maximal monotone if，moreover，for［x1，y1］∈Rd×Rd，〈x1−x2，y1−y2〉≥0，for all［x2，y2］∈A，implies［x1，y1］∈A.Here，〈·，·〉denotes the inner product，and|·|the usual norm on Rd. We also denote S（Rd×d）the d×d-matrix with the Euclid norm‖·‖，and A−1the set｛［y，x］：［x，y］∈A｝.

Consider the differential inclusion

where A is a maximal monotone operator on Rd，b：Rd→Rd，and σ：Rd→S（Rd×d）are continuous mappings.equipped with the usual metric on Rdforms a complete，separable metric space.｛W（t），t∈R+｝is a standard d-dimensional Brown motion valued in Rddefined on a stochastic basis（Ω，F，P）.Below，Cb（D）denotes the set of all bounded continuous functions on D，Lipb（D）the set of all bounded Lipschitz continuous functions on D with the Lipschitz constant Lip（f），and VTthe set of all continuous Rd-valued finite variation functions on［0，T］.

Define the set ATassociated with A by

Our starting point is a result from p.211 in［7］.

Theorem 1.1Assume that the following basic conditions hold true.

（A）0∈Int（D（A））.

（σ）‖σ（x）−σ（y）‖2≤Cσ|x−y|2for any x，y∈Rd.

（b1）〈x−y，b（x）−b（y）〉≤β|x−y|2for some β＜−Cσ/2，Cσ＞0，and any x，y∈Rd.

（b2）〈x，b（x）〉≤ι（1+|x|2）−α|x|qfor some α＞0，ι≤−Cσ，q＞1，and any x，y∈Rd.（b3）|b（x）|≤δ（1+|x|q−1）for some δ＞0 and any x∈Rd.

Then，there exists a unique pair of continuous-adapted processes（u，K）such that

（i）（u（·，ω），K（·，ω））∈AT，for any T＞0，and

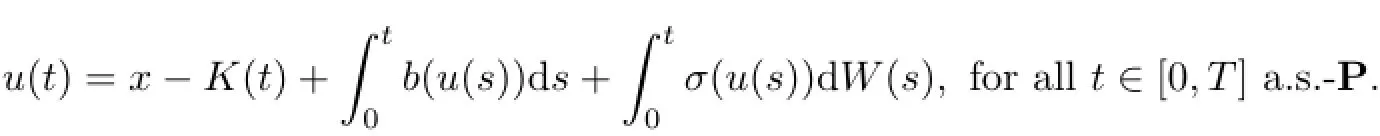
（ii）For any p≥1，

where C≡C（T，p，q，α，β，µ，γ，|A0|），and|K|0Tis the variation of K on［0，T］.

（iii）The semigroup Ptf（x）：=E［f（u（t，x））］on Cb（D）satisfies that，for any f∈Lipb（D），

（iv）There exists a unique invariant measure ν for｛Pt｝t∈R+in the sense that

Below，we call the pair（u，K）satisfying（i）in Theorem 1.1 a solution of（1）.

Remark 1.2The parametersµ，γ in（ii）come from［7，Proposition 3.4］such that Bγ：=｛x∈Rd：|x|≤γ｝⊂D（A），andµ：=sup｛|y|：y∈Ax，x∈Bγ｝is independent of A.The result（iii）is the so-called e-property of the semigroup.Here，ι in（b2）can generally be in R，and for our needs we restrict it such that ι≤−Cσ.

For each n∈N，consider

where An，bn，σnsatisfy the same conditions as（1.1）in Theorem 1.1 with the identical constants independent of n.Then，there exist a unique solution（un，Kn），and a unique invariant measure νnfor each Pntf（x）：=E［f（un（t，x））］，for x∈Dn，f∈Cb（Dn），and t＞0.

Throughout this article，we always suppose that each equation satisfies the basic conditions in Theorem 1.1，and that D=D（A）=D（An）.Our main result is

Theorem 1.3Assume that q＞4，and that

（σn）

（bσn）For any compact set

（An）There exists γ0＞0 such that（Jn）For any fixed λ＞0 and compact setwhere

Then，νnweakly converges to ν as n→+∞.

Remark 1.4Note that the Yosida approximationof A is singlevalued，maximal monotone on Rd，and Lipschitz continuous with the Lipschitz constantThe condition（An）particularly indicates that

where A0x：=projAx（0）for x∈D（A），and projAxdenotes the projection on Ax.

Remark 1.5If A is a maximal monotone operator on Rd，and x is an interior point of D（A），then A is locally bounded at x，that is，there exists a neighborhood U of x such thatAx is bounded in Rd，seeing p.30 of［1］.This fact shows that condition（An）is not so amazing.

2　Proofs

Next，we go through the procedures：（i）To prove the tightness of｛νn｝n∈N；（ii）To prove that ν in（iv）of Theorem 1.1 is the only possible limit point for the sequence.These are the contents of the following two subsections.

2.1Tightness

Proposition 2.1Λ：=｛νn｝n∈Nis tight.

ProofOn the one hand，set

By Itˆo's formula for un，first with respect to|x|2，and then to ϕδ（t），using（A）of An，for fixed y∈An0，we have

where Qσn，W（s）is symmetric，definite matrix associated with σn，W，and Tr（Qσn，W（s））=1. Here，we have used the Lipschitz property of σn，and the fact that

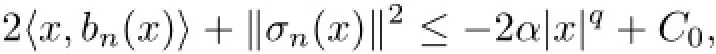
which are implied by（σ）and（b2）.Therefore，we have

As q＞4，by Young's inequalitywith r∗the conjugate number of r，

Integrating both sides with respect to νn，by the invariance，we know

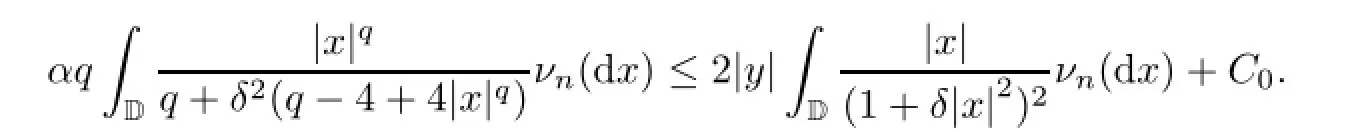
Letting δ→0，we obtain

On the other hand，the fact that t≤1+tq，t∈R+yields Choosing r sufficiently large，due to q＞1，we obtain

现代标准化是应用系统工程学的概念、系统分析方法，从标准化对象整体出发，使各部门充分协调一致来进行标准化工作。[1]现代标准化活动的首要特点是注重系统性，即标准化必须从系统的观点处理问题，并且要建立同技术水平和生产规模相适应的标准系统。由于现代企业本身就是复杂的系统，建立企业标准体系，通常要遵循标准系统理论。

Here，C1and C2are positive constants independent of x and n by（An）.Set BR=｛x∈Rd：|x|≤R｝，then

Thus，the set Λ is tight by the definition.

2.2Identification of limit points

At the end of this subsection，we shall prove

Proposition 2.2All the limit points of Λ are identical with ν.

For each λ＞0，consider the approximating equation of（1.1）

Then，we need

Lemma 2.3For each λ＞0，there exists a unique solution uλfor（2.1），and for any p≥1，，where C3is a positive constant independent of λ.

Due to the monotonicity of Aλand|Aλ0|≤|A00|，we obtain

where|A00|＜+∞by（A）of A.Similarly，from（b1）and（b3）of b，we can get

Finally，Gronwall's inequality implies

Similarly，by Itˆo's formula

f

or|uλ（t）|2with respect to ψ∈（t）：=（t+ǫ）p，ǫ＞0，we can show our results.For each fixed x∈D，set

where ρ is a mollifier with suppρ⊂（0，1），ρ∈C∝（R），andR10ρ（s）ds=1.

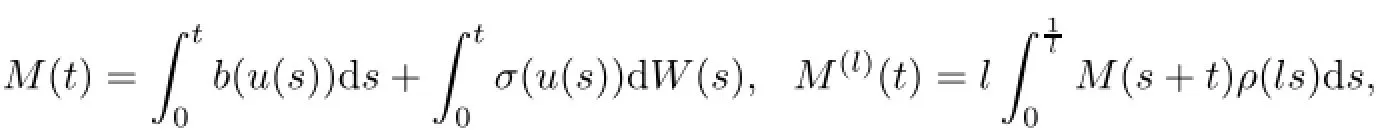
points denote the derivative with respect to t.

and

Set

and

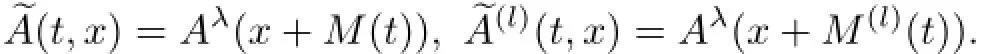
Then，the above equations change into

The existence of the solutionsis ensured by the Lipschitz property of~A and~A（l）. Next，we divide our arguments into two steps.

Step 1Show

Consider the equation

The existence of the solution u（l）is ensured by［3，Theorem 3.2］.As

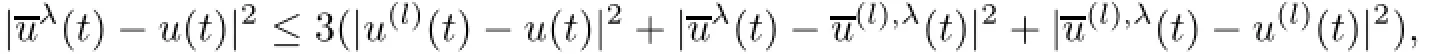
we shall show our assertion using the following three sub-steps.

By［3，Proposition 4.3］，we have

Because，by（ii）in Theorem 1.1，we have known

with the help of（ii）in Lemma 2.4，it is sufficient to show E|≤C4，where C4＞0 is a constant independent of l.In fact，for 0≤s，t≤T，by［7，Proposition 3.4］，we obtain

Because

by（ii）in Lemma 2.4 and Gronwall's inequality，we can show our claim.

Because

and the fact that

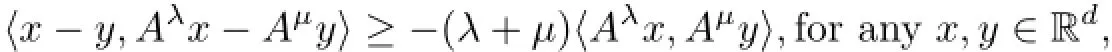
which is implied by the definition of Aλand the monotonicity of A，thus

From the inequality behind（4.29）in［3］，we know

and thus

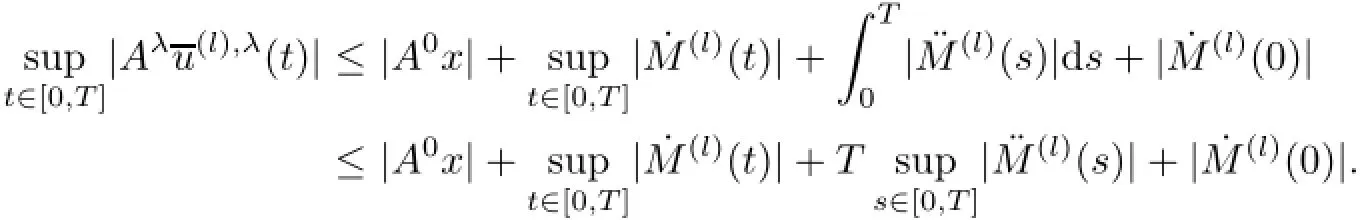
As D=D（A），and the fact that x∈D（A）⇔|A0x|＜+∞，（iv）in Lemma 2.4 implies where C5is a positive constant independent of λ andµ.The proofs of［3，Proposition 4.7］show

Then，our claim follows by the completeness.

Due to the above three claims，we can finish Step 1 by the ǫ−λ technique.

Step 2By Itˆo's formula，we have

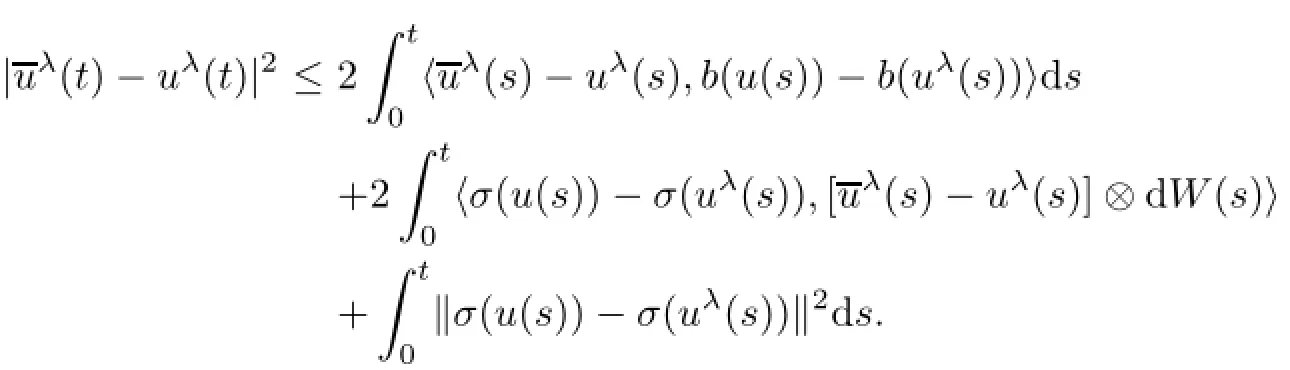
The second term on the right side can be estimated as

Therefore，we obtain

According to Lemma 2.3，

Due to Step 1，then for any ǫ＞0，there exists λ0＞0 such that whenever λ＜λ0，

that is，

Gronwall's inequality implies

Finally，we can complete the proof by the ǫ−λ technique.

Next，for each λ＞0，consider the approximating equation of（1.3），

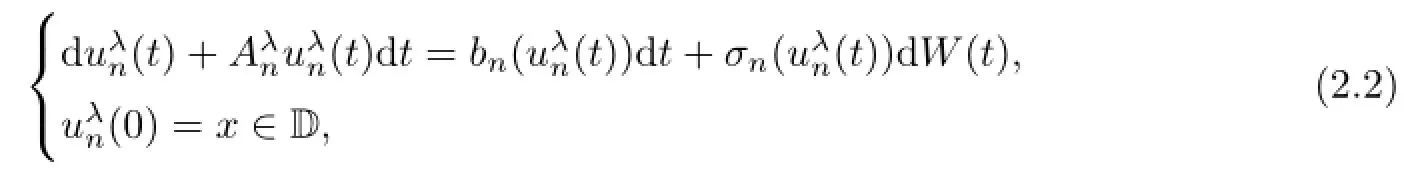
Lemma 2.6For each n∈N and λ＞0，there exists a unique solutionof（2.2），and for any p≥1，is a positive constant independent of n，λ.

ProofThe proof is similar to Lemma 2.3，and only note that，by（An）+∞.

Lemma 2.7For each x∈D，we have

ProofBy（An）and（σn），we can show it by the same arguments as Lemma 2.5.

Lemma 2.8For each fixed λ＞0，x∈D，

ProofBy Itˆo's formula

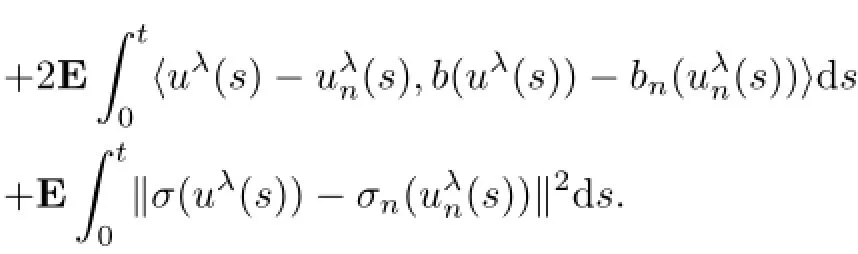
On the one hand，due to the monotonicity of the Yosida approximation，and the elementary inequality 2ab≤a2+b2，we know

Consider，for any R＞0，

The Lipschitz property of the Yosida approximation and（An）imply|x|），where C（λ）：=.Hence，by Lemma 2.3，for any ǫ＞0，there exists an R0＞0 such that

For fixed R0，using（Jn）and，there exists an N1∈N such that whenever n＞N1，II＜Tǫ.On the other hand，due to（b1）of bnand the elementary inequality，we obtain

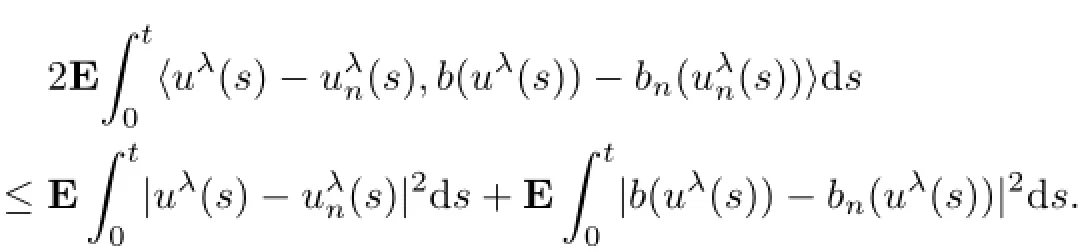
Similarly，by（bσ），（b3），and Lemma 2.3，the result，then for any ǫ＞0，there exists an N2∈N such that whenever n＞N2，

By（σ）of σn，（σn），（bσ），and Lemma 2.3，for any ǫ＞0，there exists an N3∈N such that whenever n＞N3，

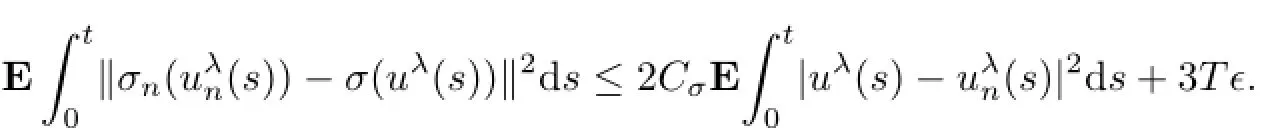
In the whole，for any ǫ＞0，there exists N≡（N1∨N2∨N3）∈N such that whenever n＞N，

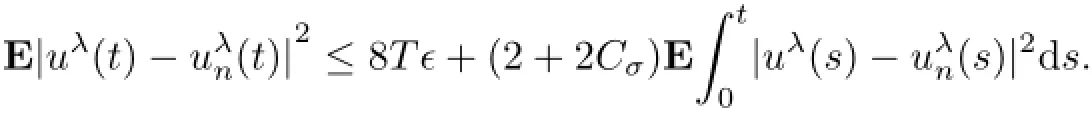
Gronwall's inequality yields E|uλ（t）−uλn（t）|2≤8Tǫexp［（2+2Cσ）T］，which completes the assertion by the ǫ−N technique.

Lemmas 2.5，2.7，and 2.8 immediately yield

Remark 2.10In the deterministic situation，the above result is called Trotter's theorem；see［11］for linear case，［12］for accretive one，and［13］in p.387 for maximal monotone one. Proposition 2.9 was studied in the reflecting boundary case in［15，16］with A=1 1Othe indicator function of a convex set O.

Now，it is ready to prove Proposition 2.2 by the methods from［14］.

Proof of Proposition 2.2Suppose thatdenoted still byis a subsequence of，which is weakly convergent to ν′.Next，it is sufficient to show that ν′is an invariant measure of，and then the uniqueness of the invariant measure implies ν′=ν，which can complete the proof.In fact，for any f∈Lipb（D），t≥0，we have

By the invariance and the weak convergence，the first term converges to zero.By Proposition 2.9 and Lebesgue's dominated convergence theorem，the third term converges to zero.By the e-property（1.2）of the semigroup，we have

Proof of Theorem 1.3Propositions 2.1 and 2.2 complete the proof.

Remark 2.11There are some equivalent characteristics of condition（Jn）（see pp.361-65 in［13］），and sufficient conditions p.29 in［1］.Some examples are given in［17，18］.

Remark 2.12For the MSDE of Wiener-Poissontype，we can consider the similar problem based on the article［19］.

AcknowledgementsThe authors would like to thank Doctor J.M.Tüolle for his help to solve several puzzles.

References

［1］Br´ezis H.Op´erateurs Maximaux Monotones et Semi-groupes de Contractions dans les Espaces de Hilbert. North-Holland：Amsterdam，1973

［2］Kr´ee P.Diffusion Equation for Multivalued Stochastic Differential Equations.J Funct Anal，1982，49：73-90

［3］C´epa E.Probl`eme de Skorohod Multivoque.Ann Probab，1998，26：500-532

［4］Ren J，Wu J，Zhang X.Exponential Ergodicity of Non-Lipschitz Multivalued Stochastic Differential Equations.Bull Sci Math，2010，134：391-404

［5］Wu J，Zhang H.Penalization Schemes for Multi-valued Stochastic Differential Equations.Statist Probab Lett，2013，83：481-492

［6］R˘a¸scanu A.Deterministic and Stochastic Differential Equations in Hilbert Spaces Involving Multivalued Maximal Monotone Operators.Panamer Math J，1996，6：83-119

［7］Zhang X.Skorohod Problem and Multivalued Stochastic Evolution Equations in Banach Spaces.Bull Sci Math，2007，131：175-217

［8］Barbu V，Da Prato G.Ergodicity for Nonlinear Stochastic Equations in Variational Formulation.Appl Math Optim，2006，53：121-139

［9］Ciotir I.A Trotter-type Theorem for Nonlinear Stochastic Equations in Variational Formulation and Homogenization.Differential Integral Equations，2011，24：371-388

［10］Z˘alinescu A.Second Order Hamilton-Jacobi-Bellman Equations with an Unbounded Operator.Nonlinear Anal，2012，75：4784-4797

［11］Trotter H F.Approximation of Semi-groups of Operators.Pacific J Math，1958，8：887-919

［12］Br´ezis H，Pazy A.Convergence and Approximation of Semigroups of Nonlinear Operators in Banach Spaces. J Functional Analysis，1972，9：63-74

［13］Attouch H.Variational Convergence for Functions and Operators.Pitman Advanced Publishing Program，1984

［14］Ciotir I，Tüolle J M.Convergence of Invariant Measures for Singular Stochastic Diffusion Equations.Stochastic Process Appl，2012，122：1998-2017

［15］Kaneko H，Nakao S.A Note on Approximation for Stochastic Differential Equations//Lect Note Math 1321.Berlin：Springer，1988：155-162

［16］Rozkosz A，Silomi´nski L.On Stability and Existence of Solutions of SDEs with Reflection at the Boundary. Stochastic Process Appl，1997，68：285-302

［17］Ciotir I.A Trotter Type Result for the Stochastic Porous Media Equations.Nonlinear Anal，2009，71：5606-5615

［18］Ren J，Wu J，Zhang H.General Large Deviations and Functional Iterated Logarithm Law for Multivalued Stochastic Differential Equations.J Theor Probab，2015，28（2）：550-586

［19］Wu J.On Wiener-Poisson Type Multivalued Stochastic Differential Equations With non-Lipschitz Coefficients.Acta Math Sin，2013，29B（4）：675-690

October 29，2014；revised March 19，2015.This work is supported by NSFs of China（11471340 and 11461028）