TOPOLOGICAL ENTROPY OF PERIODIC COVEN CELLULAR AUTOMATA∗

Weibin LIU（刘伟斌） Jihua MA（马际华）

School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China

E-mail∶weibinliu@whu.edu.cn；jhma@whu.edu.cn



TOPOLOGICAL ENTROPY OF PERIODIC COVEN CELLULAR AUTOMATA∗

Weibin LIU（刘伟斌） Jihua MA（马际华）

School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China

E-mail∶weibinliu@whu.edu.cn；jhma@whu.edu.cn

We investigate topological entropy of periodic Coven cellular automatas；that is，the maps FB∶｛0，1｝Z→｛0，1｝Zdefined by

Cellular automata；periodic word；topological entropy

2010 MR Subject Classification37B15；37B40；68Q80

1　Introduction

Cellular automata（CA，for short）was originally introduced by von Neumann and Ulam［23］in 1966 for modeling biological self-reproduction.In the mathematical literature，CA was initiated by Hedlund［15］in symbolic dynamical system as endomorphisms of the shift dynamical system in 1969，and in the next year，Conway［13］proposed his famous“game of life”，which received remarkable attention.In the early 1980s，Wolfram［26，27］studied computational aspects of CAs and classified CAs into four classes according to their behavior on finite configurations.

The topological entropy of a dynamical system was presented in［1］and now it is a widely accepted measure of the complexity of dynamical systems.It is well known that the topological entropy of CAs is undecidable in general［16］，however，there are numerous examples of CAs for which it is computable.For example，D'amico，Manzhi and Margara［10］computed the topological entropy of D-dimensional（D≥1）linear CAs over the ring Zm（m≥2）and provided an algorithm for computing the topological entropy of positively expansive CAs in 2003.

In 1980，Coven［5］computed topological entropy of a class of CAs，that is，the maps FB：｛0，1｝Z→｛0，1｝Zinduced by block maps fB：｛0，1｝r+1→｛0，1｝such that

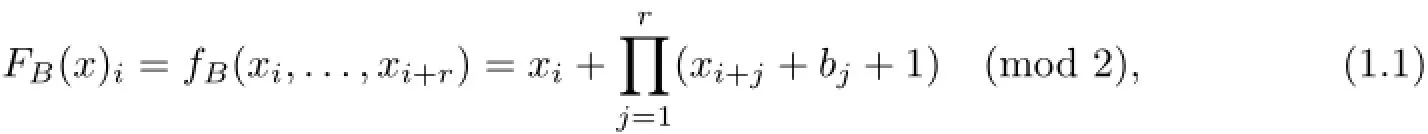
where the r-block word B=b1···br∈｛0，1｝r（r≥2）was aperiodic（see Definition 2.1）.And he proved that the topological entropy of these CAs was log2.In 1996，Blanchard and Maass［3］called those CAs studied in［5］aperiodic Coven CAs，and showed that aperiodic Coven CAs were regular，contained equicontinuous points without being equicontinuous，and were chain transitive but not topologically transitive.Therefore，the following problem was raised in［8］.

Problem 1.1（Problem 4，［8］）Let（｛0，1｝Z，FB）be a cellular automata whose local rule satisfies Eq.（1.1）with r≥2.For periodic B=b1···br∈｛0，1｝r，it is not known whether（｛0，1｝Z，FB）is positive entropy，topologically transitive，chain transitive or sensitive.

In this article，we partially answer this problem when B=b1···bris a periodic r-block word except 0rand 1r，whereThroughout this article，（｛0，1｝Z，FB） is called a Coven CA if its local rule satisfies Eq.（1.1）with r≥2 and the r-block word B= b1···br∈｛0，1｝r.If B is a periodic（resp.aperiodic）word，then，（｛0，1｝Z，FB）is called a periodic（resp.aperiodic）Coven CA.

Here and throughout this article，the set P（B）denotes the set of all periods of B（see Definition 2.1），and write m=min｛p：p∈P（B）｝，Bi=b1···bifor 1≤i≤r，and for any positive real number a，we denote by「a」the integral part of a.According to the Fine-Wilf periodicity lemma［11，20］，we divide the set of periodic r-block words into four subsets Γ1，Γ2，Γ3，and Γ4as below.

It is clear that Γ1，Γ2，Γ3，and Γ4are disjoint pairwise and｛0，1｝rcan be decomposed into the disjoint union

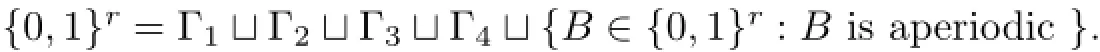
Our first main result is the following.Let h（X，T）denote the topological entropy of a dynamical system（X，T）.

Theorem 1.2Let（｛0，1｝Z，FB）be a periodic Coven CA with a periodic block word B∈｛0，1｝r｛0r，1r｝.

（1）If B∈Γ1，then，h（｛0，1｝Z，FB）=log2；

（2）If B∈Γ2，then，h（｛0，1｝Z，FB）=h（｛0，1｝Z，F1k）where k=rm；

（3）If B∈Γ3⊔Γ4，then，we have

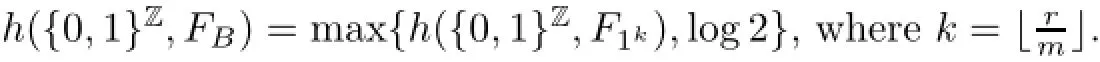
Remark 1.3For the Coven CA（｛0，1｝Z，FB）with B=0kor 1k，we are not able to determine their topological entropy.

In［5］，Coven constructs a subsystem such that topological entropy of the subsystem is equal to that of the whole system.The main difficulty in this article is to construct a subsystem as that in［5］.Due to periodicity of the block word，we construct two subsystems so that topological entropy of the whole system equals the maximization of that of two subsystems.In particular，when the block words belong to Γ1，both of them have the same topological entropy log2.

In［19］，K˚urka divides CAs（AZ，F）into four classes according to the existence of equicontinuous points.Denote by ε the set of equicontinuous points of（AZ，F）.

（K1）ε=AZ；

（K2）∅6=ε 6=AZ；

（K3）（AZ，F）is sensitive（that is，ε=∅）but not positively expansive；

（K4）（AZ，F）is positively expansive.

We show that any periodic Coven CA is not sensitive by the definition and hence not topologically transitive for the periodic word B∈｛0，1｝r｛0r，1r｝.

Theorem 1.4Let（｛0，1｝Z，FB）be a periodic Coven CA with B∈｛0，1｝r｛0r，1r｝，then，（｛0，1｝Z，FB）belongs to（K2）.It follows that（｛0，1｝Z，FB）is not topologically transitive.

As a corollary，it follows that a periodic Coven CA is almost one-to-one when the periodic word B∈｛0，1｝r｛0r，1r｝.Here and throughout，the symbol“♯”stands for“the cardinality of”.

Corollary 1.5Let（｛0，1｝Z，FB）be a periodic Coven CA with a periodic block word B∈｛0，1｝r｛0r，1r｝，and let D be the collection of all x∈｛0，1｝Zsuch that the forward and backward σ-orbits are dense in｛0，1｝Z，that is， Then，FBis almost one-to-one and♯F−1B（｛y｝）=1 for every y∈D.

This article is organized as follows.In Section 2，we introduce basic definitions and notions. In Section 3，we study some propositions of periodic Coven CAs and deal with Theorem 1.4 and Corollary 1.5.Theorem 1.2 is proved in Section 4.

2　Preliminaries

In this section，we will introduce some basic definitions and notions on dynamical systems and cellular automata.Readers may refer to［17，18，21，23，25］for more details.

2.1Symbolic Dynamical Systems

Let N be the set of nonnegative integers，Z be the set of integers，and A be a finite alphabet set with discrete topology and♯A≥2.We write Anfor the set of all n-letter words over A and A∗for the set of finite words on A.Denote by|u|the length of a word u∈A∗.For two words u，v，we say that u is a factor of v，if v=aub，for some a，b∈A∗.If a is empty，then，u is called a prefix of v；if b is empty，then，u is called a suffix of v；if both a and b are not empty，then，u is called a interior factor of v.

Consider the set AZof the two-sided infinite sequence x：=（xi）i∈Z，where xi∈A.Write=ui···ujfor i≤j in Z.Endow AZwith the product topology and define the shiftσ：AZ→AZby σ（x）=（xi+1）i∈Zfor any x=（xi）i∈Z.A fundamental basis of closed and open sets of AZis the family of cylinder sets

where u∈A∗and i∈Z，that is，any point ofi［u］i+|u|−1has the same factor u from i to i+|u|−1.It is clear that AZis compact，metrizable and one metric compatible with this topology is the following：

The endomorphism（AZ，σ）is called a two-sided full shift.

Definition 2.1（［20］）Let u=u1···un∈Anbe a finite word.We say a word u is periodic if there is at least one p，1≤p≤n−1，such that ui=ui+pfor 1≤i≤n−p.The number p is called a period of u.The set of all periods of u is denoted by P（u）and m=min｛p：p∈P（u）｝is called the minimal period of u.A word u is aperiodic if P（u）=∅.

For example，let u=001000，then，P（u）=｛4，5｝and m=4.

Remark 2.2If u∈Anand m=min｛p：p∈P（u）｝，then，m=1 if and only if u=anfor some a∈A.

A dynamical system is a couple（X，T），where X is a compact set called the state space，and T：X→X is a continuous self-map.Let ϕ：X→Y between two dynamical systems（X，T）and（Y，S）be a continuous mapping such that ϕ◦T=S◦ϕ.If ϕ is bijective，then，we say（X，T）and（Y，S）are conjugacy.If ϕ is injective，then，we say（X，T）is a subsystem of（Y，S）.If ϕ is surjective，then，we say（Y，S）is a factor of（X，T）.

2.2Cellular Automata

The map F：AZ→AZis called a CA if it is continuous and commutes with σ.Hedlund［15］gives an equivalent statement：there exist r1，r∈N and a local rule f：Ar1+r+1→A such that

for every x∈AZ.The nonnegative integers r1and r are called the left and right radius of the CA respectively.If r1=0，we say that（AZ，F）is one-sided.A one-sided CA is generally restricted to ANand denoted by（AN，F）.We say（AZ，F）is right-permutative if for any u∈Ar1+rand any b∈A，there exists a unique a∈A such that f（ua）=b.Likewise，（AZ，F）is left-permutative if for any u∈Ar1+rand any b∈A，there exists a unique a∈A such that f（au）=b.A closed set X⊆ANis F-invariant if F（X）⊆X.

We recall the definitions of some topological properties of CAs.

Definition 2.3（［18］）Let（AZ，F）be a CA.

（1）（AZ，F）is equicontinuous at x if for any ǫ＞0，there exists δ＞0 such that

（2）（AZ，F）is almost equicontinuous if the set of equicontinuous points is a residual set.

（3）（AZ，F）is sensitive if there exists ǫ＞0 such that

（4）（AZ，F）is positively expansive if there exists ǫ＞0 such that

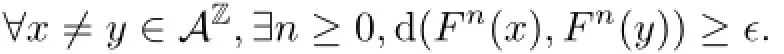
Remark 2.4By comparing the definitions of sensitive and equicontinuous，one can easily see that

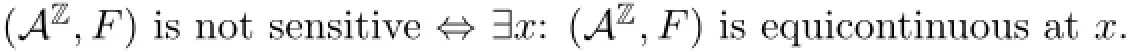
2.3Topological entropy of CA

In this section，we introduce two equivalent definitions of topological entropy；readers may refer to［25］and［16］for more details.

Bowen gives the definition of topological entropy using separating sets.Let n∈N，ǫ＞0，and K be a compact subset of AZ.A set E of K is called（n，ǫ）-separating with respect to the map F，if x，y∈E，x 6=y，we have dn（x，y）＞ǫThe topological entropy of（K，F）is defined by

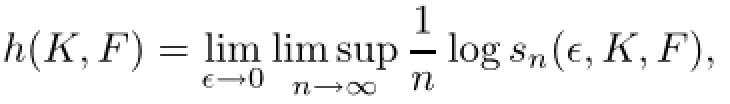
where sn（ǫ，K，F）is the largest cardinality of any（n，ǫ）-separated subset of K with respect to the map F.

In［16］it is shown that for one dimension cellular automata，the general definition of topological entropy translates to the following form.Let R（w，t）be the number of distinct rectangles of width w and height t occurring in a space-time evolution diagram of（AZ，F）（see Figure 1 from［10］）.It is easily to see that

Figure 1R（w，t）is the number of distinct rectangles of width w and height t occurring in（AZ，F）

Given w and t，the number R（w，t）will be determined by computing the evolution of all block word of length w+（r1+r）（t−1）.The topological entropy of（AZ，F）is given by

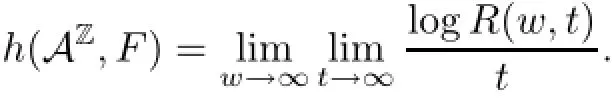
From the above，it follows that the topological entropy of（AZ，F）is finite and satisfies

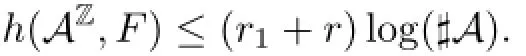
The following properties of topological entropy will be very helpful in the sequel.

Proposition 2.5（［18］）Let（X，T）and（Y，S）be two dynamical systems.

（1）If（X，T）is a subsystem of（Y，S），then，h（X，T）≤h（Y，S）.

（2）If（Y，S）is a factor of（X，T），then，h（Y，S）≤h（X，T）.

Corollary 2.6（［12］）Let（X，T）be a dynamical system，and suppose that X is a metric space and a union of a collection｛Xi：i∈J｝of closed T-invariant subsets of X，then，

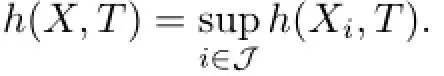
3　Equicontinuity and Almost One-to-Oneness

In this section，we mainly study some topological propositions of periodic Coven CAs.In［3］，Blanchard and Maass showed that aperiodic Coven CAs were in class（K2）.Theorem 1.4 implies that periodic Coven CAs are also in class（K2）and Corollary 1.5 reveals that periodic Coven CAs are almost one-to-one for the periodic word B∈｛0，1｝r｛0r，1r｝.

Recall that（｛0，1｝Z，FB）is a periodic Coven CA，if FB（x）iequals xi+1（mod 2）when xi+1···xi+r=B and equals xiotherwise，where B=b1···bris a given periodic word.And P（B）is the set of all periods of B and we call m=min｛p：p∈P（B）｝the minimal period of B. The following notations will be useful.Let~0=1，~1=0 and for an n-block C=c1···cn−1cnwith n≥2，let~C=c1···cn−1~cn.

Proposition 3.1Every periodic Coven CA is not positively expansive.

ProofLet（｛0，1｝Z，FB）be a periodic Coven CA with a periodic block word B=b1···br. The proof will be divided into two cases.

Case 1.Assume that B∈｛0r，1r｝，that is to say，b1=···=br=0 or 1.For any ǫ=2−s＞0，we choose two points x=such that

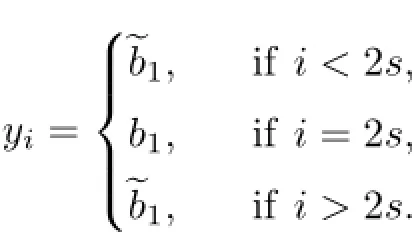
Case 2.Assume that the periodic word B∈｛0，1｝r｛0r，1r｝.It follows that the minimal period m of B satisfies m≥2.For any ǫ=2−s＞0，we also choose two points x=andsuch that

Both x and y in Case 1 or Case 2 are fixed points so that

Therefore，（｛0，1｝Z，F）is not positively expansive.

ProofDefine ϕ：｛0，1｝Z→｛0，1｝Zby ϕ（x）i=xi+1（mod 2），then it is easy to verify that ϕ is a bijective and continuous mapping such thatis conjugate to

Proof of Theorem 1.4Notice that the minimal period m of B satisfies m≥2 because the periodic word B∈｛0，1｝r｛0r，1r｝.The proof will be divided into two parts.

First，we shall prove that there is an equicontinous point in（｛0，1｝Z，FB）.That is to say，（｛0，1｝Z，FB）is almost equicontinous by Remark 2.4 and Proposition 5.12 of［18］.

Now，it suffices to show that there exists a point which is not an equicontinuous point. Because the minimal period m≥2，we can choose the fixed point y=（yi）i∈Zsuch that

which is the required point.

As mentioned above，（｛0，1｝Z，FB）belongs to（K2）.By［7］，it follows that（｛0，1｝Z，FB）is not topologically transitive.

A continuous map T：X→X of a compact metric space X is said to almost one-to-one if the set｛x∈X：T−1（T（x））=｛x｝｝is residual in X.If a CA F：AZ→AZis surjective andµ is the uniform Bernoulli measure on AZ，then，there is a connection between hµ（AZ，F）being zero and F being almost one-to-one on AZ.This is given by Theorem 1 of［22］.

Theorem 3.3（［22］）Let F：AZ→AZbe a a surjective cellular automata，andµbe the uniform Bernoulli measure on AZ.If hµ（AZ，F）=0，then，F is almost one-to-one.

Proof of Corollary 1.5From Theorem 1.4，（｛0，1｝Z，FB）has at least one equicontinuous point for B∈｛0，1｝r｛0r，1r｝，and（｛0，1｝Z，FB）is surjective，then，hµ（｛0，1｝Z，FB）=0 for the uniform Bernoulli measureµby Proposition 5.2 of［24］.Hence，FBis almost one-to-one by Theorem 3.3 and=1 for every y∈D by Corollary 2 of［22］.

4　Calculating Topological Entropy of Periodic Coven CAs

This section is contributed to the proof of Theorem 1.2.Before so doing，we introduce the famous Fine-Wilf periodicity lemma（Lemma 4.1），which leads to classifications of the set ofperiodic block words，and then，we give an example，which reveals the importance of Theorem 1.2.

Lemma 4.1（［11，20］）If u is a finite word having period p and q with q≤p.If|u|≥p+q−gcd（p，q），where gcd（p，q）denotes the greatest common divisor of p and q，then，u also has period gcd（p，q）.

ProofFor the proof，readers can see Theorem 8.1.4 of［20］for details.

From the above lemma，we divide the set of periodic r-block words into four subsets Γ1，Γ2，Γ3，and Γ4（see Section 1）.

Before proving Theorem 1.2，we see the following two examples first.

Example 4.2In Table 1 of［14］，Guibas and Odlyzko describe 116 different legal correlations for｛0，1｝20.In summary，the number of aperiodic words，Γ1and Γ2are 281076，765534 and 306 respectively，and the remaining 1660 periodic words belong to Γ3⊔Γ4.From Theorem of［5］，281076 aperiodic Coven CAs have the same topological entropy log2.From Theorem 1.2，765534 periodic Coven CAs corresponding to the word which belongs to Γ1also have the same topological entropy log2.

Example 4.3Let（｛0，1｝Z，FB）be a periodic Coven CA with the periodic block word B∈｛0，1｝r｛0r，1r｝.

（1）For B=001001=（001）2，we have h（｛0，1｝Z，FB）=h（｛0，1｝Z，F11），where（｛0，1｝Z，F11）is also a periodic Coven CA with F11（x）i=xi+xi+1·xi+2.

（2）For B=010010=（010）2or B=0100100=（010）20，we obtain

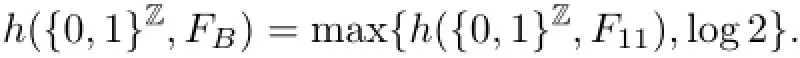
（3）For B=0100，we see h（｛0，1｝Z，FB）=log2.

Recall that（｛0，1｝Z，FB）is a periodic Coven CA，if FB（x）iequals xi+1（mod 2）when=B and equals xiotherwise，where B=b1···bris a given periodic word.And P（B）is the set of all periods of B and we write Bi=b1···biand

For example，B=001000，then，~P（B）=｛4，5，6｝and

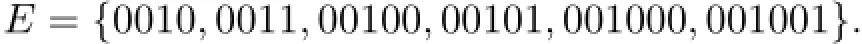
The mapping~F acting on ENis considered as FBrestricted in EN，we denote~F by FBfor convenience.So，ENis a closed and FB-invariant set of｛0，1｝N.

The trick of the proof of Theorem 1.2 is to construct two one-sided subsystems（EN，FB）and（｛Bm，~Bm｝N，FB）so that h（EN，FB）=h（｛0，1｝Z，FB）（Lemmas 4.4 and 4.5）and（｛Bm，~Bm｝N，FB）is conjugate to some（｛0，1｝N，F1k），where k depends on B（Lemma 4.7）.Finally，we compare the topological entropy of（EN，FB）with that of（｛Bm，~Bm｝N，FB）according to classifications of periodic words（Lemmas 4.8 and 4.9）.

After these preparations，we are able to compute the topological entropy of a periodic Coven CA by verifying the following five lemmas.Let O，then，closed and FB-invariant subset of｛0，1｝N.

Lemma 4.4Let（｛0，1｝Z，FB）and（｛0，1｝N，FB）be two Coven CAs with any block word B∈｛0，1｝r，then，

ProofFrom［16］，for given width w and height t，one gets the same number R（w，t）on｛0，1｝Zand｛0，1｝N.Therefore，h（｛0，1｝Z，FB）=h（｛0，1｝N，FB）.

Lemma 4.5If B∈｛0，1｝r，then，h（EN，FB）=h（｛0，1｝N，FB）.

ProofSuppose that B∈｛0r，1r｝.We consider B=1r（the case B=0ris similar），the minimal period of B is 1，thus，we have EN=｛0，1｝N.There is nothing to prove.

Suppose that B∈｛0，1｝r｛0r，1r｝.That is to say，the minimal period m of B satisfies m≥2，hence，EN｛0，1｝N.The method of the proof is similar to that of Theorem of［5］.

To begin with，（EN，FB）is regarded as a subsystem of（｛0，1｝N，FB），hence，we have

Now，according to Corollary 2.6（［12］），it suffices to show thatfor each point x∈｛0，1｝N.

In fact，each x∈｛0，1｝Nmust belong to one of the following situations.

（S1）x∈EN；

（S2）B appears infinitely often in x but σk（x）/∈ENfor all k≥0；

（S3）x/∈ENbut σk（x）∈ENfor some k≥1；

（S4）B appears only finitely often in x.

Case（S1）.Because ENis a closed and FB-invariant subset of｛0，1｝N，we infer thatEN，therefore，h（O（x），FB）≤h（EN，FB）.

Case（S2）.We can write x=A1C1A2C2···AnCn···using the following procedure.Recall that~P（B）=P（B）∪｛r｝，and

Step 1.Underline the occurrence of B in x.Label the nonunderlined block by V1，V2，··· and label the block before V1by W0（W0may be empty）and the block between Vkand Vk+1by Wkfor k≥1.Obviously，Wk=Bp1···BplB∈E∗for some l and pj∈~P（B），1≤j≤l. Therefore，the point x can be written as

Step 2.Let VkWk=with∈（E｛B｝）∗，and Vk，16∈E∗（Vk，1may be empty）such that any suffix of Vk，1does not belong to E.Then，we set

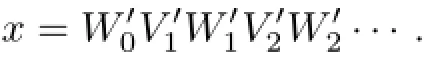
Step 5.Let Ci=for i≥0 and Aj=for j≥1，then，we obtain the required decomposition.

The decomposition x=C0A1C1A2C2···AnCn···has the following properties：

（P1）Ci6=∅for i≥1；

（P2）B does not appear in Ai；

（P3）Aidoes not end with any element of E；

（P4）Ci∈E∗and ends with B for every i≥1.If C06=∅，so is C0.

Recall that|u|denotes the length of the finite word u.Now，write FB（x）=···，where||=|Ai|and||=|Ci|.From Proposition 4.6 behind this lemma，we imply that the decomposition FB（x）=···also has properties（P1）-（P4）.For each n≥1，（x）=···，where|，also has properties（P1）-（P4）.

Case（S3）In a manner similar to Case（S2），）is conjugate to the product of a rotation on a finite group andfor some y∈EN.Hence，

Case（S4）Because B appears only finitely often in xis conjugate to a rotation on a finite group according to the definition of FB，thus，

In conclusion，by Corollary 2.6（［12］），

Therefore，this lemma is proved.

Proposition 4.6Let x belong to Case（S2）in the above lemma.If the decomposition···has properties（P1）-（P4），and···，where，then，the decomposition FB（x）also has properties（P1）-（P4）.

Proof

（1）（P1）is clear.

（2）Suppose that B appears infor some i in FB（x）.Because fB：｛0，1｝r+1→｛0，1｝is the local rule of FB，for convenience，fBis also denoted by the map from｛0，1｝n+rto｛0，1｝nfor any integer n≥1.Because of periodicity of B，we have

where P（B）is the set of all periods of B.It follows that an element ofmust appear in the same positions in x.Because B does not appear in Aiand B appear in，thus，orB~B appears in Aior AiCi.Because B does not appear in Ai，this appearance of B must entirely in Ci，and by Step 2 of Lemma 4.4，B~pB andB~B must entirely in Citoo，contrary to

（4）Let Ci=E1E2···EsB，where each Ej∈E，and let D be the initial r-block ofBy the local ruleJ，whereand J= fB（BD）.Because B must in，thus，D 6=B.If B is an interior block of BD，then，this interior factor B must in Ciby Step 1 of Lemma 4.4.Hence，B is not an interior factor of BD. Therefore，J=B.

Lemma 4.7For B∈｛0，1｝r｛0r，1r｝，the subsystem）is conjugate to（｛0，1｝N，F1k）where k=，and hence

In particular，if B∈Γ1，then，ProofLet（｛0，1｝N，）be a periodic Coven CA defined by

where k，m，and bmdepend on B.And define φ：｛0，1｝N→｛Bm，~Bm｝Nby

the mapping φ is continuous and bijective，and satisfies φ◦=FB◦φ，then，（｛0，1｝N，）is conjugate to

If bm=1，then（x）=（x），∀x∈｛0，1｝N.In the case of bm=0，by Proposition 3.2，（｛0，1｝N，Fbkm）is conjugate to（｛0，1｝N，F1k）.Therefore，

In particular，if B∈Γ1，then，we have k=1，that is，F1k=F1with

ProofAssume that B∈Γ1.For each p∈~P（B），define a map

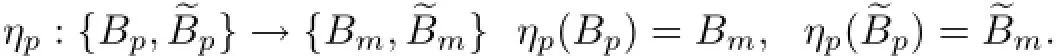
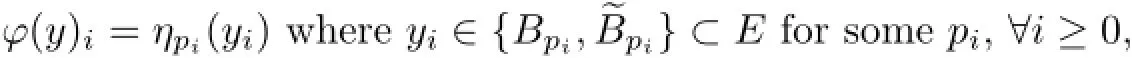
Let a mapping ϕ：EN→｛Bm，~Bm｝Nbe defined bythen，the mapping ϕ is continuous and surjective，but not injective.By Bowen's definition of topological entropy，for each y∈EN，there exists ϕ（y）∈｛Bm，~Bm｝Nsuch that

From Corollary 2.6（［12］），h（EN，FB）=h（｛Bm，~Bm｝N，FB）.

Suppose that B∈Γ2，then there exists k≥2 such that r=km and

Because Bmis aperiodic，it follows that ENand｛Bm，~Bm｝Nare identical，therefore，

Lemma 4.9If B∈Γ3⊔Γ4，then，

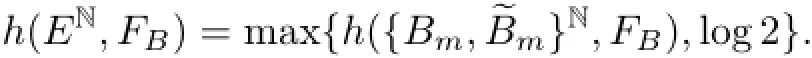
ProofWe only show that the lemma holds when B∈Γ4；the rest is analogous.

Suppose that B∈Γ4，and write B=（Bm）kBt，where k≥2 and 1≤t＜m.Observing that both｛Bm，~Bm｝Nand｛B，~B｝Nare closed and FB-invariant subsets of EN，and（｛B，~B｝N，FB）is conjugate to（｛0，1｝N，τ）with τ（x）i=xi+xi+1（mod 2），we see that

Then，in a manner similar to B∈Γ1，by Bowen's definition of topological entropy，we have

LetbE=EE，then we deduce thatbENand｛Bm，~Bm｝Nare identical.Therefore，

Repeated application of Lemma 4.5 enables us to obtainIn fact，for any x in EN，let N1and N2denote the number of occurrences of elements ofin x and the number of occurrences of elements ofbE in x，respectively.The following table describes topological entropy of

x∈ENN1N2h（O（x），FB）case 1finiteinfinite≤h（｛Bm，~Bm｝N，FB）case 2infinitefinite≤log2 case 3infiniteinfinite≤log2

If x∈ENbelongs to case 1，by Bowen's definition of topological entropy，for l large enough，for someTherefore，

If x∈ENbelongs to case 2，for l large enough，sn（l，O（x），FB）≤2n，thus，

If x∈ENbelongs to case 3，let

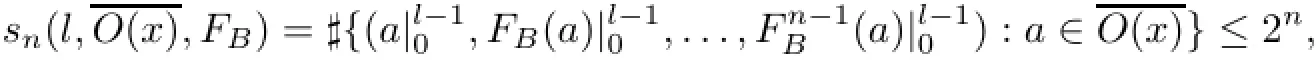
Proof of Theorem 1.2From Lemmas 4.4 and 4.5，we have

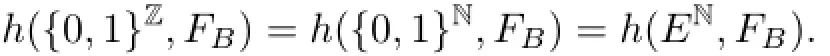
Suppose that B∈Γ1，from Lemmas 4.7 and 4.8，we obtainlog2.

Suppose that B∈Γ2，from Lemmas 4.4，4.7，and 4.8，it follows that

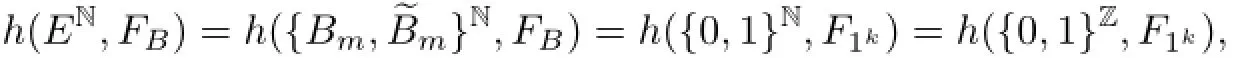
Suppose that B∈Γ3⊔Γ4，from Lemmas 4.4，4.7，and 4.9，we have

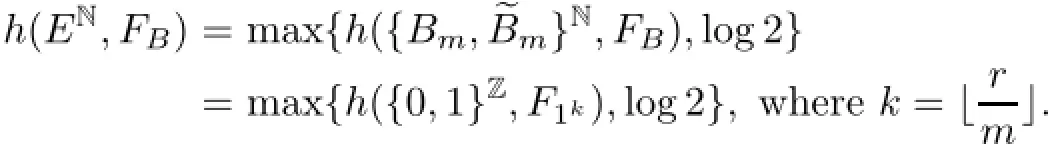
Thus，the proof is completed.

From［2］it follows that the positive topological entropy implies chaotic in the sense of Li-Yorke.Thus，the following proposition is provided.

Proposition 4.10Let（｛0，1｝Z，FB）be a periodic Coven CA with the periodic block word B∈｛0，1｝r｛0r，1r｝.If B belongs to Γ1⊔Γ3⊔Γ4，then，（｛0，1｝Z，FB）is chaotic in the sense of Li-Yorke.

Example 4.11Table 1 of［14］also reveals that most of Coven CAs have positive entropy and then，they are chaotic in the sense of Li-Yorke.From Theorem of［5］and Theorem 1.2，we imply that at least 1048270 Coven CAs are chaotic in the sense of Li-Yorke with respect to 220=1048576 Coven CAs.

5　Conclusion

In this article，we compute the topological entropy and discuss topological transitive and sensitive when the periodic word B∈｛0，1｝r｛0r，1r｝.However，for B∈｛0r，1r｝，this is still an open problem.

References

［1］Adler R，Konheim A，McAndrew M.Topological entropy.Trans Amer Math Soc，1965，114：309-319

［2］Blanchard F，Glasner E，Kolyada S.On Li-Yorke pairs.J Reine Angew Math，2002，547：51-68

［3］Blanchard F，Maass A.Dynamical behaviour of Coven’s aperiodic cellular automata.Theoret Comput Sci，1996，163：291-302

［4］Blanchard F，Tisseur P.Some properties of cellular automata with equicontinous points.Ann Inst Henri Poincar´e，2000，36：569-582

［5］Coven E M.Topological entropy of block maps.Proc Amer Math Soc，1980，78：590-594

［6］Coven E M，Hedlund G A.Periods of some nonlinear shift registers.J Combina Theory，1979，27A：186-197

［7］Codenotti B，Margara L.Transitive cellular automata are sensitive.Amer Math Monthly，1996，103：58-62

［8］Delorme M，Formenti E，Mazoyer J.Open problem on cellular automata.Technical report RR-2000-25. ´Ecole Normale Sup´erieure de Lyon，2000

［9］Denker M，Grillenberger C，Sigmund K.Ergodic Theory on Compact Space.Berlin：Springer-Verlag，1976［10］D’amico M，Manzhi G，Margara L.On computing the entropy of cellular automata.Theoret Comput Sci，2003，290：1629-1646

［11］Fine N J，Wilf H S.Uniqueness theorem for periodic functions.Proc Amer Math Soc，1965，16：109-114

［12］Goodman T N T.Relating topological entropy and measure entropy.Bull London Math Soc，1971，3：176-180

［13］Gardner M.Mathematical Games-The fantastic combinations of John Conway’s new solitaire game“life”. Sci Am，1970，223：120-123

［14］Guibas L J，Odlyzko A M.Periods in strings.J Combin Theory，1981，30A：19-42

［15］Hedlund G A.Endomorphisms and automorphisms of the shift dynamical system.Math Syst Theory，1969，3：320-375

［16］Hurd L P，Kari J，Culik K.The topological entropy of cellular automata is uncomputable.Ergodic Theory Dynam Systems，1992，12：255-265

［17］Kitchens B.Symbolic Dynamical，One-sided，Two-sided and Countable State Markov Shifts.Berlin：Springer，1998

［18］K˚urka P.Topological and Symbolic Dynamics.Cours Sp´ecialis´es-Collection SMF，2003

［19］K˚urka P.Languages，equicontinuity and attractors in cellular automata.Ergodic Theory Dynam Systems，1997，17（2）：417-433

［20］Lothaire M.Algebraic Combinatorics on Words.Cambridge：Cambridge University Press，2002

［21］Lind D，Marcus B.An Introduction to Symbolic Dynamics and Coding.Cambridge：Cambridge University Press，1995

［22］Moothathu T K S.Surjective cellular automata with zero entropy are almost one-to-one.Chaos Solitons Fractals，2011，44：415-417

［23］von Neumann J.Theory of Self-reproducing Automata.Urbana：University of Illinios，1966

［24］Tisseur P.Cellular automata and Lyapunov exponents.Nonlinearity，2000，13：1547-1560

［25］Walters P.An Introduce to Ergodic Theory.New York：Springer-Verlag，1982

［26］Wolfram S.Computation theory of cellular automata.Comm Math Phys，1984，96：15-57

［27］Wolfram S.Theory and Application of Cellular Automata.Singapore：World Scientific，1986

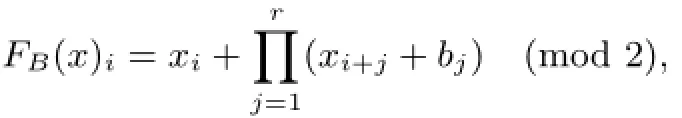
November 20，2014；revised June 2，2015.The first author is supported by the Fundamental Research Funds for the Central Universities（2012201020204），and the second author is supported by NSFC（11171128，11271148）.

where B=b1b2···br∈｛0，1｝r（r≥2），is a periodic word.In particular，we prove that if the minimal period of B is greater thanr2，the topological entropy is log2.