RECURRENCE FOR WEIGHTED TRANSLATIONS ON GROUPS∗

Chung-Chuan CHEN（陈中川）

Department of Mathematics Education，National Taichung University of Education，Taiwan

E-mail∶chungchuan@mail.ntcu.edu.tw



RECURRENCE FOR WEIGHTED TRANSLATIONS ON GROUPS∗

Chung-Chuan CHEN（陈中川）

Department of Mathematics Education，National Taichung University of Education，Taiwan

E-mail∶chungchuan@mail.ntcu.edu.tw

Let G be a locally compact group，and let 1≤p＜∞.We characterize topologically multiply recurrent weighted translation operators on Lp（G）in terms of the Haar measure and the weight function.We also show that there do not exist any recurrent weighted translation operators on L∝（G）.

Topologically multiple recurrence；recurrence；hypercyclicity；locally compact group；Lp-space

2010 MR Subject Classification37B20；47A16；43A15

1　Introduction

Recently，we gave sufficient and necessary conditions for weighted translation operators on groups to be hypercyclic and chaotic in［1-4］，which subsumes some works in［5-8］.The notion of hypercyclicity in linear dynamics is close to，but stronger than the notion of recurrence in topological dynamics in［9］.It is well known that every hypercyclic operator is recurrent on separable Banach spaces in［10］.However，this is not the case for topologically multiple recurrence，which is a stronger notion than recurrence.There exists a hypercyclic weighted backward shift on ℓ2（Z）in［10］，which is not topologically multiply recurrent.In this note，we will give a sufficient and necessary condition for weighted translation operators on the Lebesgue space Lp（1≤p＜∞）of a locally compact group to be topologically multiply recurrent in terms of the Haar measure and the weight function，and show，on the L∝space，there are no recurrent weighted translation operators.

In linear dynamics，we first recall that an operator T on a Banach space X is called hypercyclicifthereexistsavectorx∈XsuchthatitsorbitunderTdenotedby Orb（x，T）：=｛x，Tx，T2x，···｝is dense in X in which x is said to be a hypercyclic vector of T.It is known that hypercyclicity is equivalent to topological transitivity.An operator T is topologically transitive if given two nonempty open subsets U，V⊂X，there is some n∈N such that TnU∩V 6=∅.If TnU∩V 6=∅from some n onwards，then T is called topologically mixing.Hypercyclicity and transitivity have been studied by many authors.We refer to these books［11，12］on this subject.In topological dynamics，an operator T is topologically multiplyrecurrent if for every positive integer N and every nonempty open set U in X，there is some n∈N such that U∩T−nU∩T−2nU∩···∩T−NnU 6=∅.If N=1，then T is called recurrent，that is，the condition U∩T−nU 6=∅is satisfied.

The motivation to connect hypercyclicity with recurrence is inspired by the works in［9，10］. In［10］，Costakis and Parissis characterized topologically multiply recurrent weighted shifts onℓp（Z）in terms of the weight sequence.On the other hand，that the space ℓ∝（Z）does not support any recurrent weighted shifts was shown in［9］.We note that the weighted shifts onℓp（Z）and ℓ∝（Z）are a special case of the weighted translation operators on the Lebesgue space of a locally compact group.In this article，we will extend some results in［9，10］to the setting of translations on groups.

In what follows，let G be a locally compact group with identity e and a right-invariant Haar measure λ.We denote by Lp（G）（1≤p≤∞）the complex Lebesgue space，with respect to λ.A bounded function w：G→（0，∞）is called a weight on G.Let a∈G and let δabe the unit point mass at a.A weighted translation on G is a weighted convolution operator Ta，w：Lp（G）−→Lp（G）defined by

where w is a weight on G and Ta（f）=f∗δa∈Lp（G）is the convolution：

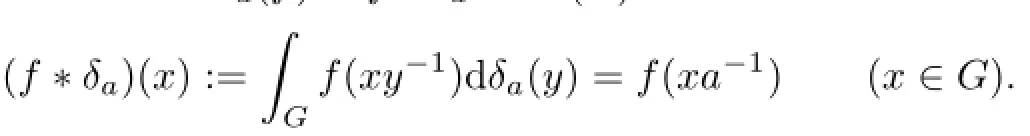
If w−1∈L∝（G），then the weighted translation operatorais the inverse of Ta，w. We write Sa，wforto simplify notation.We assume w，w−1∈L∝（G）throughout.

2　Recurrence on Lp（G）

In this section，we will prove the result on Lp（G）（1≤p＜∞）for translations by aperiodic elements in G.An element a in a group G is called a torsion element if it is of finite order. In a locally compact group G，an element a∈G is called periodic（or compact）in［4］if the closed subgroup G（a）generated by a is compact.We call an element in G aperiodic if it is not periodic.For discrete groups，periodic and torsion elements are identical.It is proved in［4］that an element a∈G is aperiodic if and only if for any compact set K⊂G，there exists some N∈N such that K∩Ka±n=∅for all n＞N.

We will make use of the aperiodic condition to obtain the result below.We note that［4］in many familiar non-discrete groups，including the additive group Rd，the Heisenberg group，and the affine group，all elements except the identity are aperiodic.

Theorem 2.1Let G be a locally compact group and let a be an aperiodic element in G. Let 1≤p＜∞and Ta，wbe a weighted translation on Lp（G）.The following conditions are equivalent.

（i）Ta，wis topologically multiply recurrent；

（ii）For each N∈N and each compact subset K⊂G with λ（K）＞0，there is a sequence of Borel sets（Ek）in K such that λ（K）=limk→∝λ（Ek）and both sequences（for 1≤l≤N）admit，respectively，subsequences）and）satisfying

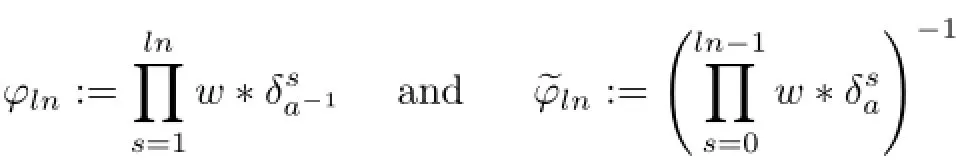
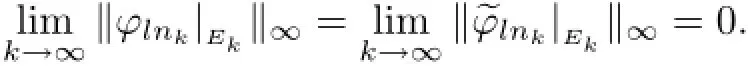
Proof（i）⇒（ii）.Let Ta，wbe topologically multiply recurrent.Let K⊂G be a compact set with λ（K）＞0.Let ε∈（0，1）.By aperiodicity of a，there is some M such that K∩Ka−n=∅for n＞M.Let χK∈Lp（G）be the characteristic function of K.

by the topologically multiply recurrent assumption.Hence，there exists f∈Lp（G）such that

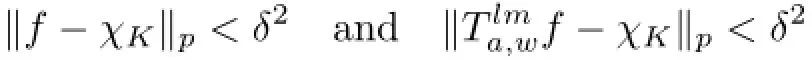
for l=1，2，...，N.Let

and

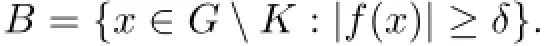
Then，we have

and

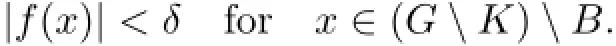
Moreover，by the inequality below，

we have λ（A）＜δp.Similarly，λ（B）＜δp.

In contrast，let

and

Then，

and

Again，by applying the inequality

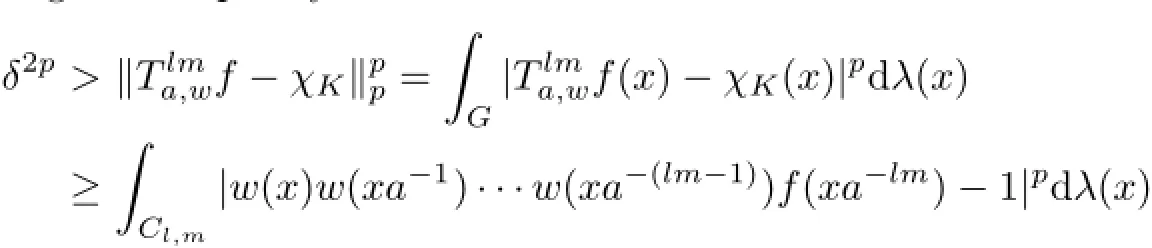
we have λ（Cl，m）＜δp.Using the similar argument and the right invariance of Haar measure，we have λ（Dl，m）＜δp.

As K∩Ka−lm=∅，we have

and

Let

Then，we have λ（KEm）＜4Nδpand‖＜ε，which implies condition（ii）.

（ii）⇒（i）.We show that Ta，wis topologically multiply recurrent.Let U be a non-empty open subset of Lp（G）.As the space Cc（G）of continuous functions on G with compact support is dense in Lp（G），we can pick f∈Cc（G）with f∈U.Let K be the compact support of f. Given some N，let Ek⊂K and the sequences（ϕln），（ϕ~ln）satisfy condition（ii）.

By aperiodicity of a，there exists M∈N such that K∩Ka±n=∅for any n＞M.Let ε＞0.There exists M′∈N such that nk＞M andfor k＞M′.Hence，

as k→∞for 1≤l≤N.By the sequence），we havel=1，2，···，N.

Now，we are ready to achieve our goal.For each k∈N，let =0 for

Then，by the aperiodicity of a，we have

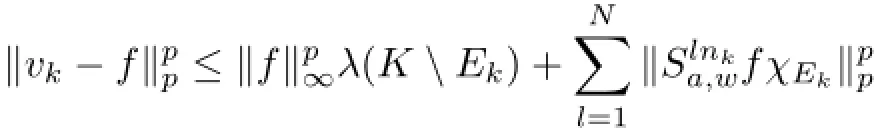
and

which implies

Example 2.2Let G=Z，a=−1∈Z which is aperiodic.Let w∗δ−1be a weight on Z. Then，the weighted translation operator T−1，w∗δ−1is given by

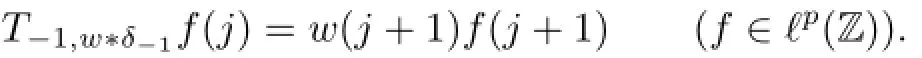
and

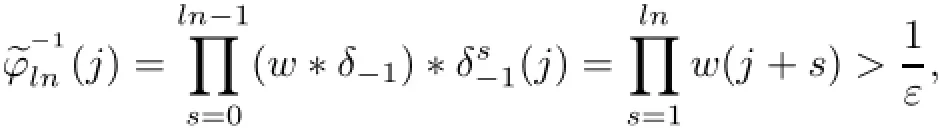
which is the condition in［10，Proposition 5.3］.

In contrast，if w−1∈ℓ∝（Z），then T1，w−1is the inverse of the operator，and the above weight conditions suffices T1，w−1to be multiply recurrent.Indeed，the weight conditions in Theorem 2.1 for T1，w−1is

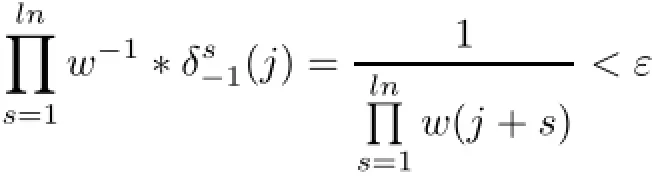
and

which is the same with the conditions for T−1，w∗δ−1.If we define w：Z→（0，∞）as

Remark 2.3In Example 2.2，bothand the inverse ofcould be multiply recurrent simultaneously.In fact，this is also true for general cases.That is，an invertible weighted translation Ta，wgenerated by an aperiodic element is multiply recurrent on Lp（G），if and only if the inverse of Ta，wis multiply recurrent.

Example 2.4Let G=R，a=3，and w be a weight on R.Then，the weighted translation T3，won Lp（R）is given by

By Theorem 2.1，the operator T3，wis topologically multiply recurrent if given ε＞0，some N∈N，and a compact subset K of R，there exists a positive integer n such that for 1≤l≤N

and x∈K，we have

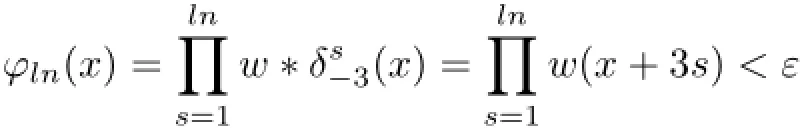
and

We may define w：R→（0，∞）by

which satisfies the above weight condition.

Example 2.5Let

be the Heisenberg group which is neither abelian nor compact.For convenience，an element in G is written as（x，y，z）.Let（x，y，z），（x′，y′，z′）∈H.Then，the multiplication is given by

and

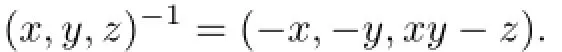
Let a=（1，0，2）and w be a weight on H.Then，a−1=（−1，0，−2）and the weighted translationon Lp（H）is given by

and

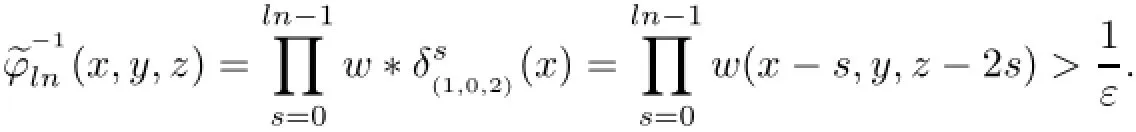
Similarly，one can obtain the required weight condition by defining w：H→（0，∞）as follows：

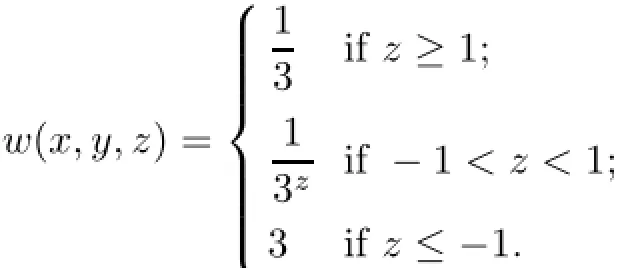
It is known that Devaney's notion of chaos consists of topological transitivity together with periodicity.That is，an operator T on a Banach space is chaotic if T is transitive and the set of periodic elements，｛x∈X：∃n∈N with Tnx=x｝，is dense in X.In［1，Corollary 2.3］，we characterize chaotic weighted translation operators on discrete groups.

Corollary 2.6（［1，Corollary 2.3］）Let G be a discrete group and let a be a non-torsion element in G.Let 1≤p＜∞and Ta，wbe a weighted translation on ℓp（G）.Then，the following conditions are equivalent.

（i）Ta，wis chaotic.

（ii）For each finite subset K⊂G，both sequences

admit，respectively，subsequences（ϕnk）and（~ϕnk）satisfying

The following corollaries reveal that both chaos on discrete groups and topological mixing on locally compact groups are stronger notions than topologically multiple recurrence.

Corollary 2.7Let G be a discrete group and let a be a non-torsion element in G.Let 1≤p＜∞and Ta，wbe a weighted translation operator on ℓp（G）.If Ta，wis chaotic，then Ta，wis topologically multiply recurrent on ℓp（G）.

ProofLet Ta，wbe chaotic on ℓp（G）.By the weight condition in Corollary 2.6，Ta，wis topologically multiply recurrent.

Corollary 2.8Let G be a locally compact group and let a be an aperiodic element in G. Let 1≤p＜∞and Ta，wbe a weighted translation operator on Lp（G）.If Ta，wis topologically mixing，then Ta，wis topologically multiply recurrent on Lp（G）.

ProofLet ε＞0 and choose 0＜δ＜ε

1+ε.Let K be a compact set of G，and let U=｛g∈Lp（G）：‖g−χK‖p＜δ2｝.Given N∈N，by the topologically mixing assumption，there exists some m∈N such that

from m onwards.Hence，

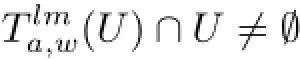
for l=1，2，···，N.Therefore，we can pick，for each l，a function fl∈U with∈U which gives

Using this for each fland repeating the arguments in the proof of Theorem 2.1，we find Borel

sets Ek⊂K such that

which says Ta，wis topologically multiply recurrent.

Example 2.9Let G=Z，a=−1∈Z and let w∗δ−1be a weight on Z.Then，is the bilateral weighted backward shift on ℓp（Z）.By Corollaries 2.7 and 2.8，the operatoris topologically multiply recurrent ifis topologically mixing or chaotic.

Remark 2.10We note that there exists a weighted shift which is topologically multiply recurrent but is neither chaotic nor topologically mixing in［13］.

To end up this section，we show that for weighted translations Ta，w，hypercyclicity is equivalent to recurrence.We，first，recall a work in［3］.

Theorem 2.11（［3，Theorem 2.1］）Let G be a locally compact group and let a be an aperiodic element in G.Let 1≤p＜∞and Ta，wbe a weighted translation on Lp（G）.The following conditions are equivalent.

（i）Ta，wis hypercyclic.

（ii）For each compact subset K⊂G with λ（K）＞0，there is a sequence of Borel sets（Ek）in K such that λ（K）=）and both sequences

admit，respectively，subsequences（ϕnk）and（~ϕnk）satisfying

Now，we state the result below.

Corollary 2.12Let G be a locally compact group and let a be an aperiodic element in G.Let 1≤p＜∞and Ta，wbe a weighted translation on Lp（G）.Then，Ta，wis hypercyclic if and only if Ta，wis recurrent.

ProofAs hypercyclicity implies recurrence，we only need to show if Ta，wis recurrent，then Ta，wis hypercyclic.

Let N=1 in Theorem 2.1，then the condition（ii）in Theorem 2.1 suffices Ta，wto be hypercyclic by Theorem 2.11.

Example 2.13It was shown in［10，Proposition 5.1］that the bilateral weighted shift onℓp（Z）is hypercyclic if and only if it is recurrent.One can obtain this result in the following way.Let G=Z，a=−1∈Z and let w∗δ−1be a weight on Z.Then，is the bilateral weighted backward shift on ℓp（Z）.By Corollary 2.12，hypercyclicity and recurrence occur onsimultaneously.

3　Recurrence on L∞（G）

It is known in［14，15］that a complex Banach space admits a hypercyclic operator if and only if it is infinite-dimensional and separable.Therefore，there is no hypercyclic weighted translation operator Ta，won L∝（G）by the fact L∝（G）is non-separable.Moreover，we will show，in this section，that the space L∝（G）does not support any recurrent weighted translation operators Ta，w.

Theorem 3.1Let G be a locally compact group and a∈G be an aperiodic element. Let w∈L∝（G）be a weight on G with w−1∈L∝（G）.Then，there does not exist recurrentweighted translation operator Ta，won L∝（G）.

ProofSuppose that Ta，wis recurrent.Let M＞1.Given a non-null compact set K，we define g（x）=M if x∈K；otherwise，g（x）=3.As Ta，wis recurrent，there exist a recurrent vector f and a positive integer n＞1 such that=∅from n onwards，‖f−g‖∝

and

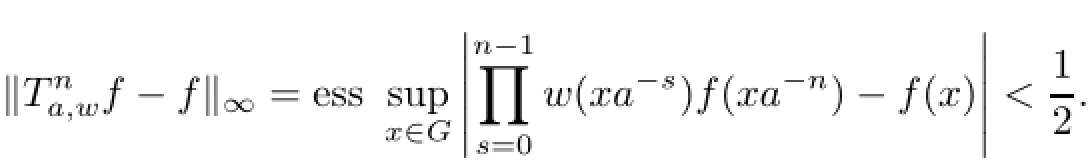
Hence，2＜|f（x）|＜4 a.e.on GK.Moreover，we have

Let E=KKa−1，then λ（E）＞0.Otherwise，K⊂Ka−1a.e.，and then Kan⊂Kan−1⊂···⊂K，which is impossible.Hence，

which implies

we arrive at

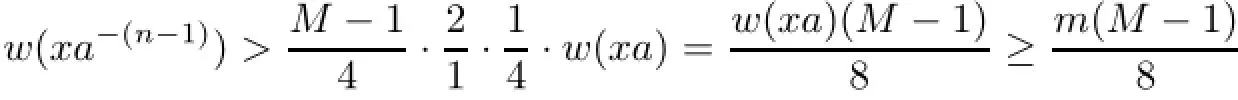
a.e.on E，where m=ess inf｛w（xa）：x∈K｝＞0 by w−1∈L∝（G）.As M can be chosen to arbitrarily large，we conclude w 6∈L∝（G）.Hence，Ta，wis not recurrent.

Example 3.2Let G=Z，a=−1∈Z and let w∗δ−1be a weight on Z.Then，is the bilateral weighted backward shift on ℓ∝（Z）.By Theorem above，there is no recurrent bilateral weighted backward shifton ℓ∝（Z）.Hence，a result in［9，Theorem 5.1］is recovered.

A well known result of Salas in［8］says that the operator I+T is hypercyclic whenever T is any unilateral weighted backward shift on ℓ2（N）.In the non-separable space L∝（G），the operator I+Ta，wcan never be recurrent on L∝（G）.

Theorem 3.3Let G be a locally compact group and a∈G.Let w∈L∝（G）be a weight on G with w−1∈L∝（G）.Let Ta，wbe a weighted translation operator on L∝（G）.Then，the operator I+Ta，wis not recurrent on L∝（G）.

ProofSuppose that I+Ta，wis recurrent.Let g（x）=1 for x∈G.Then，there exist a recurrent vector f and an arbitrarily large integer N with Nm＞2，where m=essinf｛w（x）：

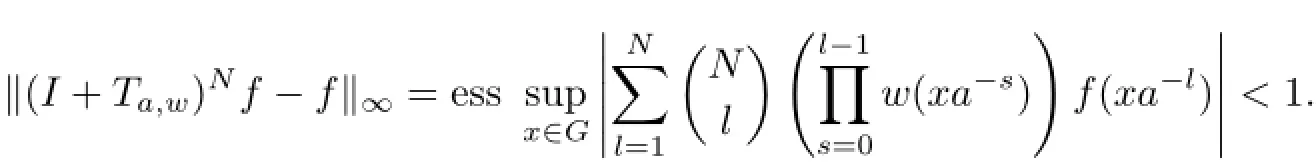
Taking real parts in the inequalities above，we have Re（f（xa−1））＞and

a.e.on G，which implies

We conclude that Nm＜2，which is a contradiction.Hence，I+Ta，wis not recurrent.

Example 3.4Let G=Z and a=0∈Z.Let w be a weight on Z.Then，the operator I+T0，wis not recurrent on ℓ∝（Z）.

References

［1］Chen C C.Chaotic weighted translations on groups.Arch Math，2011，97：61-68

［2］Chen C C.Supercyclic and Ces`aro hypercyclic weighted translations on groups.Taiwanese J Math，2012，16：1815-1827

［3］Chen C C.Hypercyclic weighted translations generated by non-torsion elements.Arch Math，2013，101：135-141

［4］Chen C C，Chu C H.Hypercyclic weighted translations on groups.Proc Amer Math Soc，2011，139：2839-2846

［5］Costakis G，Sambarino M.Topologically mixing hypercyclic operators.Proc Amer Math Soc，2004，132：385-389

［6］Grosse-Erdmann K G.Hypercyclic and chaotic weighted shifts.Studia Math，2000，139：47-68

［7］Le´on-Saavedra F.Operators with hypercyclic Ces`aro means.Studia Math，2002，152：201-215

［8］Salas H.Hypercyclic weighted shifts.Trans Amer Math Soc，1995，347：993-1004

［9］Costakis G，Manoussos A，Parissis I.Recurrent linear operators.Complex Anal Oper Th，2014，8：1601-1643

［10］Costakis G，Parissis I.Szemer`edi’s theorem，frequent hypercyclicity and multiple recurrence.Math Scand，2012，110：251-272

［11］Bayart F，Matheron´E.Dynamics of linear operators.Cambridge：Cambridge University Press，2009

［12］Grosse-Erdmann K G，Peris A.Linear Chaos.London：Springer，2011

［13］Bayart F，Grivaux S.Invariant Gaussian measures for operators on Banach spaces and linear dynamics. Proc Lond Math Soc，2007，94：181-210

［14］Ansari S I.Existence of hypercyclic operators on topological vector spaces.J Funct Anal，1997，148：384-390

［15］Bernal-Gonz´alez L.On hypercyclic operators on Banach spaces.Proc Amer Math Soc，1999，127：1003-1010

May 9，2014；revised June 17，2015.The author is supported by MOST of Taiwan（MOST 104-2115-M-142-002-）.