一种基于协方差矩阵重构的鲁棒波束形成方法

邓成晨，谢少彪，邹兴，倪涛（.上海卫星工程研究所 上海 0040；.上海航天技术研究所 上海009）

一种基于协方差矩阵重构的鲁棒波束形成方法

邓成晨1，谢少彪2，邹兴1，倪涛1
（1.上海卫星工程研究所 上海 200240；2.上海航天技术研究所 上海201109）

针对鲁棒Capon波束形成算法中采用牛顿迭代求解对角加载因子时，运算量大且算法旁瓣增益高的问题，提出了一种改进的稳健波束形成算法。首先对干扰协方差矩阵进行重构，然后将重构的协方差矩阵投影到噪声子空间，使期望信号导向矢量在噪声子空间投影最优，最后精确求解对角加载因子。该方法的运算量低于RCB算法中牛顿迭代和最差性能最优（WCPO）算法中凸规划运算，并且提高了加载因子的计算精度。实际仿真结果表明，改进算法有效克服了信号方向估计误差，具有更低且稳定的旁瓣增益，输出信干噪比性能优于现有其他方法。

鲁棒波束形成；协方差矩阵重构；对角加载；导向矢量误差；方向图畸变

常规波束形成算法在导向矢量和协方差矩阵准确已知的条件下，可以得到最优的输出信干噪比，但在实际情况下，导向矢量和采样协方差矩阵往往都存在一定的误差。而较小的误差便会引起波束形成性能的严重下降，特别是在训练数据中含有目标信号时，这种现象更为明显［1-2］。目前其解决办法多数集中在针对训练序列中改善数据协方差矩阵特性，而这类方法的代表则是对角加载技术。对角加载技术发展至今已经涌现了大量的自适应求解加载因子方法。其中，以Jian.L［3-5］为代表，首次提出了基于信号方向矢量球面不确定集约束的鲁棒波束形成（RCB）算法，这给稳健波束形成算法提供了新的求解思路。该类算法将期望信号导向矢量约束于各种不确定集中，包括多锥面不确定集［6］、球形不确定集［7-9］、椭球体不确定集［10-13］等，然而诸多方式要么采用牛顿法进行反复迭代，要么借助数学工具——凸规划来求解，使得算法计算过程复杂，计算量大大增加，不利于工程实现。

针对上述问题，本章提出了一种新的稳健波束形成方法，首先对干扰协方差矩阵进行重构，并将重构协方差矩阵投影到噪声子空间，使期望信号导向矢量在噪声子空间投影最优，并精确求解对角加载因子λ。该方法的运算量低于现有的牛顿迭代法和凸规划法，提高了加载量λ的计算精度。

1　鲁棒Capon波束形成（RCB）算法

Capon波束形成器的最优权重向量为

式（1）RX表示采样协方差矩阵，a为期望信号导向矢量，ωopt表示输出权矢量。从式（1）可知，权重向量的求解需要准确的知道信号的方向向量，但在实际的环境中，信号方向向量往往会存在偏差，波束形成器的性能会急剧下降［1］。鲁棒Capon波束形成算法代价函数为［3］

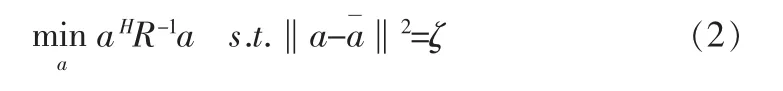
式（2）的最优解是利用Lagrange因子的方法求解得到方向向量的估计值为

式（3）中，λ为Lagrange因子，且λ＞0。从上式可以看出，求取最优导向矢量aˆ的关键在于加载因子λ的求解。为此，把式（3）代入式（2）的约束条件中，可得

对R进行特征分解RX=UΛUH，其中U为特征向量矩阵，Λ为特征值矩阵，令

将式（3）、式（5）代入式（4）可得

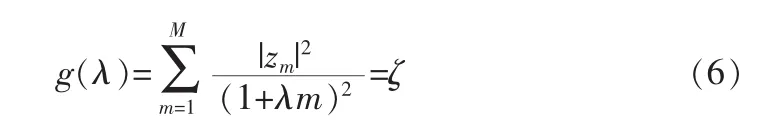
式（6）给出了λ的求解方程，λ的求取采用牛顿迭代法。然而，这一运算过程收敛速度较慢，增加了计算复杂度。下面本文将提出一种新的稳健方法，精确自适应计算加载因子。

2　改进的稳健Capon波束形成算法

2.1改进算法的基本原理

众所周知，当接收数据中包含期望信号分量时，自适应波束形成器主瓣性能将会降低，如果能将期望信号分量从接收数据中滤除，就可以提高算法的鲁棒性。基于这一思想，文献［14］提出了一种干扰加噪声协方差矩阵重构方法。干扰加噪声协方差重构矩阵表示如下

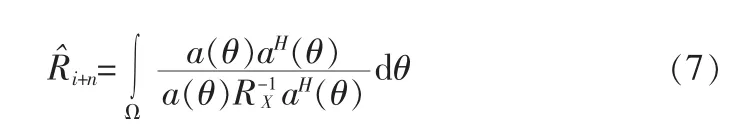
式中，RX为采样数据协方差矩阵，a（θ）为导向矢量，Rˆi+n为重构后的干扰加噪声协方差矩阵，Ω为波束旁瓣区间 （保证主瓣不在此区域）。这样通过重构干扰加噪声协方差矩阵，期望信号得到滤除，降低了大信噪比下波束主瓣增益的损失。但对于导向矢量误差，算法的性能并没有得到改善。为此，本文将引入不确定集约束的思想，基于RCB算法约束方程来求解最优导向矢量。首先，利用式（7）求解重构后的协方差矩阵Rˆi+n代替约束方程式（2）中的RX，那么最优化问题可描述成如下

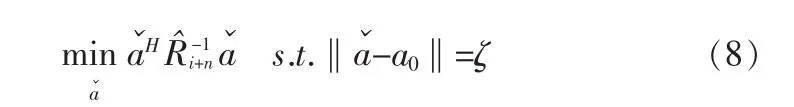
在进行分析之前，假定天线阵接收端总共有p+1＆lt;M个信号源，对重构的协方差矩阵Rˆi+n进行矩阵特征分解，则有

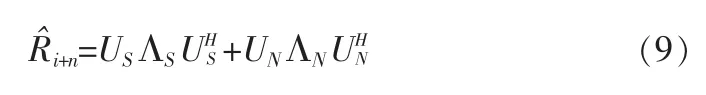
式（9）中，γ1≥γ2≥…γP+1≥γP+2≈…γM=δ2M表示Rˆi+n对应的M个特征值，ΛS=diag（γ1，γ2，…γP+1）和ΛN=diag（γP+2，…γM）分别为对应的特征值组成的对角阵US=［u1，u2，…uP+1］，UN=［uP+2，…uM］分别为信号子空间和噪声子空间，ui表示对应的特征向量。

根据矩阵特征分解理论，实际上信号导向矢量aˇ由信号子空间生成。因此aˇ可以表示成信号子空间Us的各列向量的线性组合

上式中a表示组合系数组成的列向量。把上式代入式（9）中，可得

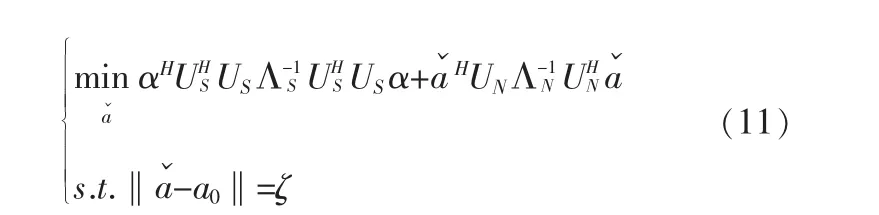
由于UHSUS=I，而由于γ1≥式（11）中，ΛN=δM2I。这样上述最优化问题可以进一步描述成如下形式

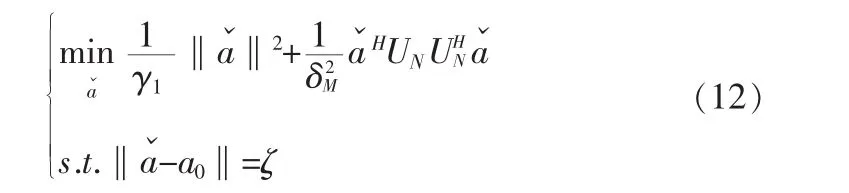
其中，δ2M表示噪声功率。由于真实的导向矢量aˇ模值为根据矩阵与向量范数相容性理论，‖USα‖V满足‖USα‖V=‖US‖F×‖α‖2。由于‖US‖F等价Tr（UHSUS）1/2，因此向量α的范数满足这里值得注意的是仅仅与阵列天线阵元数目相关，因此式（13）可以描述成如下形式

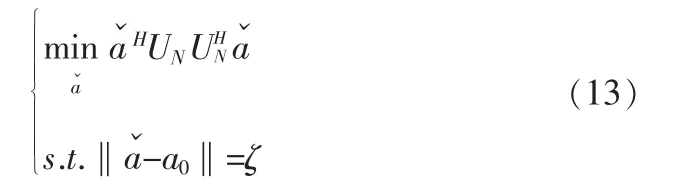
采用Lagrange因子的方法求解上式，可得最优导向矢量如下

这样问题的关键就转变成Lagrange因子的求取。将式（14）代入式（13）中的约束方程，则

由于信号子空间US和噪声子空间UN满足UNUHN+USUHS= I，因此，对式（15）中进行变换

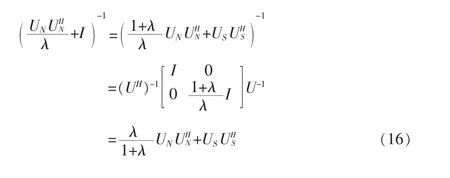
将（16）代入（15），求解λ得：

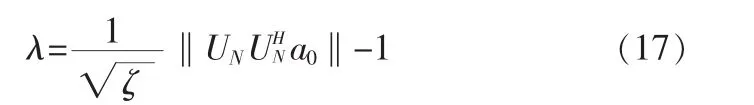
这样便得到了不确定约束集下λ的准确闭式解，将式（17）代入式（14）求得最优导向矢量ˇ。至此，干扰加噪声协方差矩阵Rˆi+n及最优导向矢量都得到求解。将其代入Capon波束形成器权值表达式，最终求得改进算法的最优权值。

从改进算法的推导过程可知，改进算法首先需要对干扰协方差矩阵进行重构，并将重构协方差矩阵投影到噪声子空间，使期望信号导向矢量在噪声子空间投影最优，并采用式（17）精确求解对角加载因子。显然，该方法的运算量低于牛顿法，提高了加载量λ的计算精度。

2.2改进算法实现步骤

既然改进算法已经得到了准确的闭式解，因而很容易得出其计算步骤，这里需要注意的是，新的稳健算法需要准确知道噪声子空间的维数。因此当干扰信号功率较强时，可以由协方差矩阵特征值的大小来准确分离出信号子空间和噪声子空间；当干扰信号功率较弱时，由于协方差矩阵特征值差异模糊，无法直接判断，这时则可以通过信源估计方法［15］。改进的稳健算法实现步骤如下

3）利用式（17）求解Lagrange因子λ；

3　数字仿真及分析

仿真中，采用50阵元的均匀线阵，并设定阵元间距固定为半波长。两个干扰信号来波方向分别为-60°和40°，其干噪比分别为40 dB和50 dB，假定期望信号来波方向为0°。改进算法中设定期望信号主瓣区间Ψ=［-3°，3°］，干扰区间Ω=［-90°，-3°］∪［3°，90°］。以下所有仿真结果均是基于200次蒙特卡洛实验。

实验一：最优导向矢量估计对波束主瓣影响分析

首先，假定期望信号真实来波方向为θ=2°，这样也就意味着导向矢量方向误差为2°。将本文算法和标准Capon算法（SCB）、WCPO算法、RCB算法进行对比，如图1所示。其中图1为4种不同算法波束方向图，图2为图1中主瓣区域局部放大图。图中可以看到，SCB方法在真实期望信号方向θ=2°上形成凹陷，而最差性能最优（WCPO）方法、RCB算法和本文算法均在此方向上形成峰值。这主要原因是SCB算法并未采取任何对协方差矩阵补偿措施，而其他3种方法均采用自适应对角类优化方法，可以较好地估计最优导向矢量，从而在真实期望信号方向上形成主瓣峰值，以保证期望信号最大化被保留。

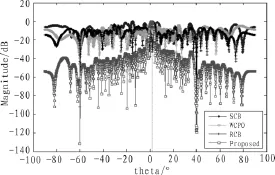
图1　指向误差为θ=2°时波束图对比

图2　图1中主瓣局部放大

实验二：快拍数、输入信噪比、主瓣宽度对波束旁瓣的影响

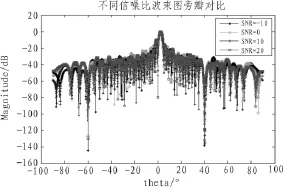
图3　输入信噪比对波束旁瓣的影响

将采样快拍数固定为L=50，输入信噪比分别设为-10 dB、0 dB、10 dB、20 dB的条件下，对比本文算法在不同输入信噪比下波束方向图帮帮性能的变化情况，如图3所示。从仿真结果可以看到，随着输入信噪比的增加，波束旁瓣增益略微有所变化，但基本维持在相对稳定的较低增益。这表明本文算法的波束旁瓣对输入信噪比的变化并不敏感，从而针对较大输入信噪比时，仍具有良好的低旁瓣增益。

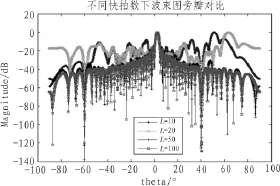
图4　快拍数对波束旁瓣的影响

图4为固定输入信噪比为0 dB时，快拍数分别为10，20，50，100情况下，本文算法的波束方向图对比。仿真结果可以看到，波束方向图的旁瓣随着快拍数增加而趋于稳定，且维持较低的增益。当快拍数不足时，旁瓣增益明显较大，然而随着快拍数增加到50时，波束旁瓣增益已经趋于稳定。快拍数不足时，由于采样点数的缺失，而采样数据的协方差矩阵得不到有效补偿，从而波束图旁瓣增益较大。

固定输入信噪比0 dB、快拍数50时，针对协方差矩阵重构中波束主瓣区域选择不同的主瓣宽度进行仿真，如图5所示。如图所示，实验中，对采样协方差矩阵重构时，分别选择主瓣宽度为2、4、6、8。从仿真结果可以看出，随着波束主瓣宽度变宽，波束旁瓣增益降低，旁瓣逐渐变小。因此可以通过改变主瓣宽度来优化旁瓣特性。

图5　主瓣宽度对旁瓣的影响

实验三：输入信噪比、波束指向偏差、快拍数对输出信干噪比（SINR）的影响

实验中，将本文算法与SCB、常规对角加载（LSMI）、WCPO、RCB算法进行对比。图6为输入不同SNR对输出SINR影响。仿真中固定采样快拍数50，并考虑指向误差θ=2°。本文算法选择波束旁瓣区间Ω=［-90°，-3°］∪［3°，90°］。LSMI算法中采用常用对角因子λ=10δ2M，其中δ2M=1表示噪声方差。

图6　输入SNR对输出SINR的影响

从图6仿真结果可以看出，所有5种算法在低输入信噪比时，性能接近或一致，尤其是在输入SNR为 0 dB以下时，更为明显。当输入信噪比逐渐增大时，SCB算法输出SINR最先下降，主要原因期望信号的存在对波束性能造成严重影响。LSMI算法采用固定的对角载入因子作为对协方差矩阵的补偿，性能要优于SCB，但随着信噪比增大，其补偿因子不能实时调整，因而造成输出信干噪比性能也急剧下降。WCPO算法和RCB算法均采用基于球形不确定约束方法，对指向偏差进行最优估计，因而克服了波束指向误差带来的问题，从而其输出 SINR性能相对较好，均优于传统的 SCB和WCPO方法。本文算法基于不确定集约束的思想上，实现采样数据协方差矩阵的重构，因而去除了期望信号对波束性能的影响，从而获取了最好的输出信干噪比性能。

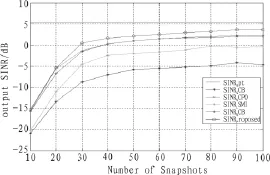
图7　采样快拍数对输出SINR的影响

图7给出了采样快拍数对波束输出信干噪比的影响。仿真中固定输入信噪比SNR=0 dB，其他条件不变。从仿真结果中可以看到，当采样快拍数不足（快拍数小于50）时，5种算法性能均较差，此时，本文算法与RCB、WCPO算法性能接近一致，并优于LSMI和SCB方法。随着快拍数的增加，5种算法输出SINR性能均有所增加，其中WCPO和RCB性能接近，且均优于LSMI和SCB算法，缘于二者都采用了自适应补偿对角加载因子，而本文算法输出SINR性能均优于其他4种方法，且接近于理想值。

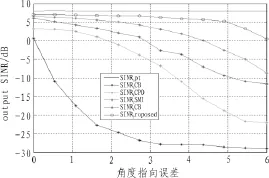
图8　波束指向误差对输出SINR影响

图8反映了波束指向偏差对输出SINR性能影响。仿真中固定输入信噪比SNR=0 dB，采样快拍数50，指向误差由0°至6°。观察仿真结果，可知随着波束指向误差的增大，5种算法输出SINR均有所下降；但就整体趋势来讲，SCB性能下降最陡峭，对波束指向误差最为敏感；其次是LSMI算法，虽然采用固定对角载入因子作为补偿，但不能实时跟踪并估计最优导向矢量；紧接着WCPO和RCB算法对指向误差具有较好的鲁棒性，这依然归功于其自适应最优导向矢量估计；而本文算法性能虽然有所下降，但下降很缓慢，且始终优于其他几种算法，因而对指向误差具有很强的鲁棒性。

4　结　论

针对信号方向估计误差波束方向图畸变问题，提出了一种基于协方差矩阵重构的稳健波束形成算法。该方法首先对干扰协方差矩阵进行重构，并将重构协方差矩阵投影到噪声子空间，使期望信号导向矢量在噪声子空间投影最优，并精确求解对角加载因子。该方法的运算量低于RCB和WCPO，因而比RCB和WCPO方法具有更简单的处理流程，运算量也大大减少。最后，针对新的稳健算法进行了实验仿真。仿真结果表明新的稳健算法性能优于现有的其他主流算法。

［1］张晓飞.阵列信号处理理论和应用［M］.北京:国防工业出版社，2010.

［2］Hongtao L I，Chen C，Zeng W，et al.Steering vector estimation based robust adaptive beamforming algorithm［J］.Chinese Journal of Radio Science，2015.

［3］Li J and Stoica P.On robust capon beamforming and diagonal loading［J］.IEEE Transactions on Signal Processing，2003，51（7）:1702-1715.

［4］Stoica P，Wang Z，Li J.Robust Capon beamforming［J］.IEEE Signal Processing Letters，2002，1（6）:172-175.

［5］Li J，Stoica P，Wang Z S.Doubly constrained robust capon beamformer［J］.IEEE Transactions on Signal Processing，2004，52（9）:2407-2423.

［6］Wu S Q，Zhang J Y.A new robust beamforming method with antenna calibration errors［C］.IEEE Wireless Communications and Networking Conference，New Orleans，L A，USA，1999，2:869-872.

［7］Vorobyov S A，Gershman A B，Luo Z Q.Robust Adaptive beamforming using worst-case performance optimization via second-order cone programming［C］.In Proc.ICASSP Orlando，FL，2002:2901-2904.

［8］Vorobyov S A，Gershman A B，Luo Z Q.Robust adaptive beamforming using worst case performance optimization:Asolution to the signal mismatch problem［J］.IEEE Transactions on Signal Processing，2003，51（2）:313-323.

［9］林静然，彭启琮，邵怀宗.一种具有双重鲁棒性的自适应波束形成算法［J］.电子测量与仪器学报，2007，21（2）:10-14.

［10］Robert G L，Stephen P B.Robust minimum variance beamforming［J］.IEEE Transactions on Signal Processing，2005，53 （5）:1684-1696.

［11］Amir B，Yonina C E.Doubly constrained robust Capon beamformer with ellipsoidal uncertainty sets［J］.IEEE Transactions on Signal Processing，2007，55（2）:753-758.

［12］刘聪锋，廖桂生.基于模约束的稳健Capon波束形成算法［J］.电子学报，2008，36（3）:440-445.

［13］林静然，彭启琮，邵怀宗，等.最坏情况下的鲁棒自适应波束形成算法性能分析［J］.电子学报，2006，34（12）:2161-2166.

［14］Kim Y L，Pillai S U，Guerci J R.Optimal loading factor for minimal samplesupport space-timeadaptiveradar［A］. Proceedings of the 1998 IEEE International Conference on Acoustics，Speech and Signal Processing，USA，1998:12-15.

［15］庄学彬，陆明泉，冯振明.一种数值稳健且低复杂度的信号子空间估计新方法［J］.电子与信息学报，2011，33（1）:90-94．

A robust beamforming algorithm based on covariance matrix reconstruction

DENG Cheng-chen1，XIE Shao-biao2，ZOU Xing1，NI Tao1
（1.Shanghai Institute of Satellite Engineering，Shanghai 200240，China；2.Shanghai Academy of Spaceflight Technology，Shanghai 201109，China）

In view of the robust Capon beamforming algorithm，the Newton iterative method is utilized to obtain the diagonal loading factor，which leads to problems of large amount of computation and high side lobe gain.This paper propose new robust beamforming algorithm.Firstly，the interference covariance matrix is reconstructed，and then the reconstructed covariance matrix is projected to the noise subspace，so that the optimum projection of the desired signal steering vector in the noise subspace can be achieved，and the diagonal loading factor is accurately solved.The computation of the proposed algorithm is less than RCB and WCPO method，which improve calculation accuracy of the load factor.Practical simulation results show that the proposed method overcomes the problem of signal direction estimation errors effectively，has a lower beam side-lobe gain than RCB and WCPO algorithm，and outcomes other existing methods.

robust beamforming；covariance matrix reconstruction；diagonal loading；steering vector error；beam pattern distortion

TN911

A

1674－6236（2016）11-0021-05

2016-03-03稿件编号：201603032

航天科技创新基金（CASC2015021）

邓成晨（1986—），男，江苏盐城人，硕士，工程师。研究方向：卫星总体方案设计。