静态推靠式旋转导向控制指令算法

王业强，李士斌，张立刚，李闯，邢恩浩，官兵

（东北石油大学石油工程学院，黑龙江 大庆 163318）

静态推靠式旋转导向控制指令算法

王业强，李士斌，张立刚，李闯，邢恩浩，官兵

（东北石油大学石油工程学院，黑龙江 大庆 163318）

旋转导向钻井系统代表了当今最高水平的定向钻进技术，而我国对该项技术的研究仍处于初级阶段，急需对该技术进行深入研究。以静态推靠式旋转导向工具为研究对象，根据其内部结构及导向工作原理，寻求针对该类型导向工具的控制指令算法。采用平面圆弧曲线假设法确定可钻达目标点的待钻井段，通过分析该井段的井斜角、井斜方位角及全角变化率，得到可实现按目标方向钻进的控制指令算法，同时将该算法编入导向工具地面控制系统。实验结果表明，该控制算法可根据轨迹要求，准确求出控制指令，实现导向功能。最后做出静态推靠式旋转导向工具的双向闭环控制图，并加以说明，以供科研人员参考。

旋转导向系统；闭环系统；平面圆弧曲线；控制指令；轨迹控制

0　引言

旋转导向钻井系统的出现，使得钻井速度和质量大幅度提高。国外各大钻井服务公司掌握着该工具的核心技术，且对各自产品进行了升级［1-2］。目前商用的系统主要有 Baker Hughes公司的 AutoTrak RCLS、Schlumberger公司的Power Drive SRD和Halliburton公司的Geo-Pilot［3］。我国对该项技术的掌握仍不成熟，且大多数研究针对井下控制部分的导向力分配［4-5］。

笔者以静态推靠式旋转导向工具为研究对象［6］，根据其内部结构及导向工作原理，寻求针对该类型导向工具的地面系统控制指令算法；并研制了一套针对静态推靠式旋转导向控制指令求解的计算软件，目前室内实验已取得良好应用效果。

1　控制指令分析

在实际钻井过程中，由于井下各种复杂因素的影响，实际井眼轨迹不可能与设计轨道完全重合，必然会产生一定的偏差。该偏差同时包括空间的距离和方向。假设当前钻进点为A，根据偏差法分析［7］，可以得到处于设计轨道上的目标逼近点C，由于实钻轨迹和设计轨道都是已知的，因此A点和C点的位置参数（包括井斜角、井斜方位角）是已知的［8］。静态推靠式旋转导向工具的控制指令包括工作效率Ak和偏置合力角αk：Ak代表偏置合力的大小，影响当前工具可以形成的全角变化率；αk决定井斜角和井斜方位角的变化。

地面控制系统的指令产生流程如图1所示。

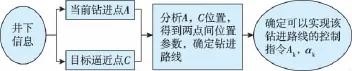
图1　地面控制系统指令产生流程

由图1可以看出：旋转导向工具的地面控制系统在接收到当前位置参数后，通过计算机分析当前点与目标点位置参数，确定一条轨道连接A，C两点，即为钻头接下来的钻进路线。笔者采用平面圆弧曲线假设法确定轨道［9］；再通过两点位置参数和轨道路线计算出该段的全角变化率及井斜、方位变化率；最后确定控制指令，传给井下控制系统。

2　工作效率的确定

假定当前钻头处于点A（XA，YA，ZA），井斜角为αA，井斜方位角为φA；目标逼近点C（XC，YC，ZC），井斜角为αC，井斜方位角为φC。画出A点方向向量nA，过nA和目标逼近点C画空间斜平面δ，则A，C两点切线交于点D，两点的法线交于点O，如图2所示。

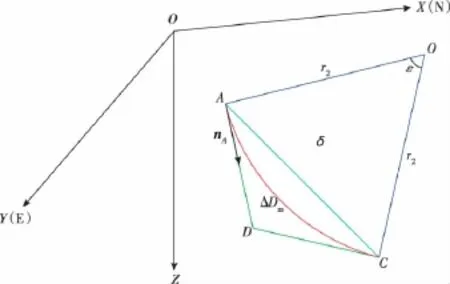
图2　空间斜平面内几何关系

已知全角变化值的计算公式为

其中

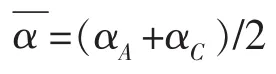
式中：ε为全角变化值，（°）；ΔαAC为井斜角的增量，（°）；ΔφAC为井斜方位角的增量为上、下两测点井斜角的平均值，（°）；αA，αC分别为当前点和目标点的井斜角，（°）。

AC段的全角变化率（狗腿变化率）为

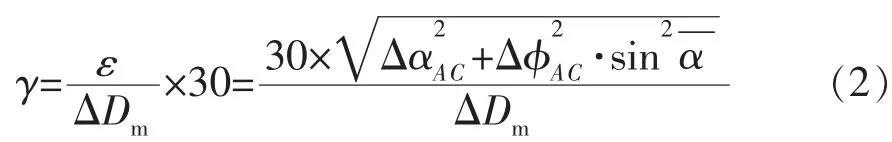
式中：γ为全角变化率，（°）/30 m；ΔDm为A点到C点之间的弧长，m。

ΔαAC，ΔφAC均为已知，要想得出该段的全角变化率，还需求出ΔDm。由图2的几何关系可知：

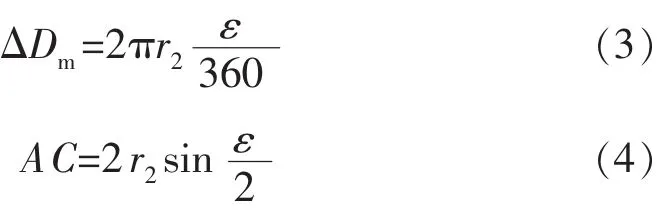
式中：r2为曲率半径，m。

这次的毕业设计,让我了解了冲压模具工艺的成形的基本原理;了解了冲压工艺的真个过程与冲压设计基本的方法;拥有拟订常规复杂冲压零件的成形工艺过程与设计普通复杂程度冲压模具成形的能力;经过这次的设计让我已经可以运用学过的基础知识,理解和解决生产过程中常见的冲压模具工艺及模具等各方面的问题。

由式（4）得

由于

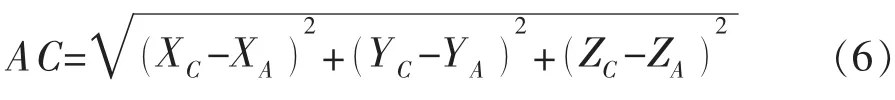
将式（6）代入式（5），得

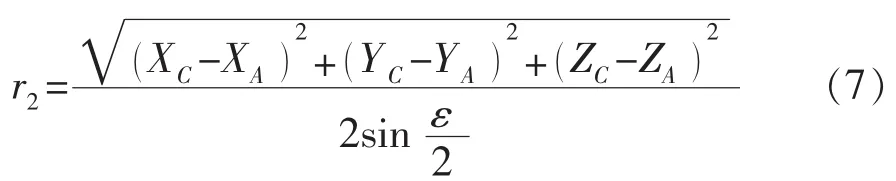
将式（7）代入式（3），得

将式（8）代入式（2），得AC段全角变化率：

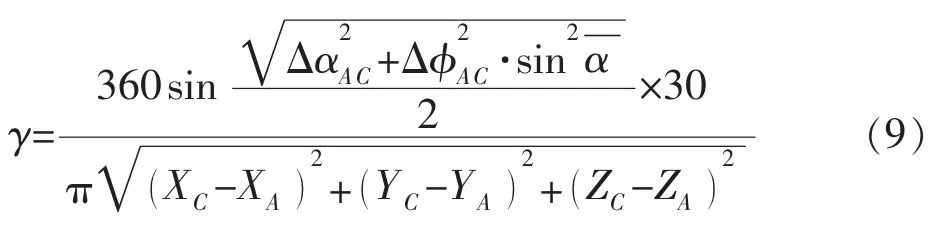
不同井下钻具组合（BHA）的旋转导向工具，具有不同的极限造斜能力。假设在当前BHA下，导向工具的极限造斜能力为γmax，即当导向工具以100%工作效率钻进时，可以钻出全角变化率为γmax的井段。同时，可以得到AC段全角变化率为γ时所对应的工作效率：

若计算得出的Ak大于100%，则表示不能按照预期的井斜角、井斜方位角钻到目标点。此时，需重新设计井眼轨道，并重新确定目标逼近点C，直至Ak不大于100%。

3　偏置合力角的确定

在井底控制平面内，定义偏置合力角αk为高边方向顺时针旋转至偏置合力的方向所转过的角度。偏置合力在整个井底控制面内，向高边方向和垂直高边方向分解为2个力——井斜力和方位力。井斜力用来改变井斜角，方位力用来改变井斜方位角。偏置合力角的大小决定井斜力和方位力的大小［10］，如图3所示。

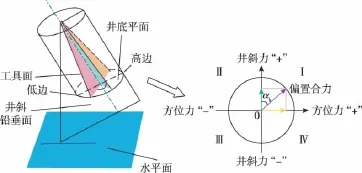
图3　控制平面内偏置合力分布示意

AC段的井斜变化率为

式中：Kα为井斜变化率，（°）/30 m。

AC段的方位变化率为

式中：Kφ为方位变化率，（°）/30 m；φA，φC分别为当前点和目标点的井斜方位角，（°）。

钻井行业中，全角变化率的标准计算图解法如图4所示。

图4　全角变化率计算图解法

1）Kα＞0，Kφ=0，此时工具处于全力增井斜角的工作模式，即井斜方位角不改变，由图4的几何关系可以得到αk=0，处于Y轴正半轴。

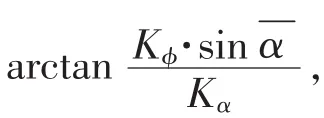
3）Kα=0，Kφ＞0，此时工具处于全力增井斜方位角的工作模式，此时井斜角不改变，由图4的几何关系可以得到αk=90°，处于X轴正半轴。

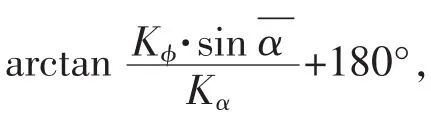
5）Kα＜0，Kφ=0，此时工具处于全力降井斜角的工作模式，井斜方位角不改变，由图4的几何关系可以得到αk=180°，处于Y轴负半轴。

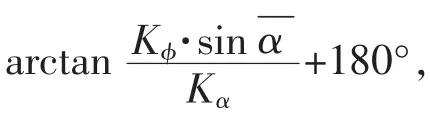
7）Kα=0，Kφ＜0，此时工具处于全力降井斜方位角的工作模式，井斜角不改变，由图4的几何关系可以得到αk=270°，处于X轴负半轴。

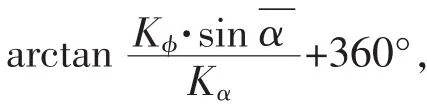
4　室内试验情况

静态推靠式旋转导向工具的控制系统下达的每一个指令，都使钻头按照一个特定的方向钻进。每个控制指令对应着一个期望的井斜变化率、方位变化率，以及在该指令下钻进井段所形成的全角变化率。基于以上控制指令算法，编写了一套针对静态推靠式旋转导向工具的控制指令计算软件（见图5）。

目前，该地面计算软件已经编入地面控制系统。经过多次的室内试验，该控制算法可以根据所需目标方向自动计算控制指令，并下达给井下执行机构。应用结果表明，计算分析的控制指令误差在允许范围内，可以精准、快速地实现导向功能。

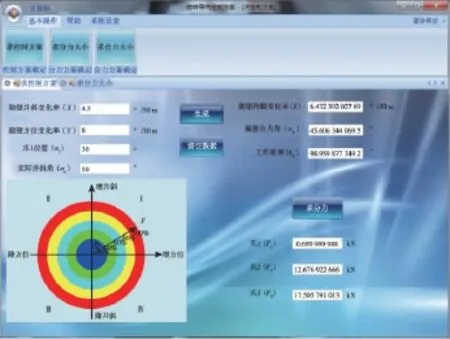
图5　控制指令计算示意

5　双向闭环控制机理

静态推靠式旋转导向工具的双向闭环控制机理如图6所示。

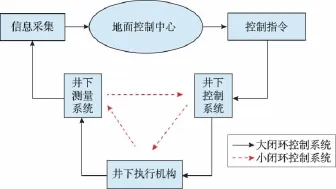
图6　双向闭环控制机理

在静态推靠式旋转导向钻井中，实现轨迹控制的方式主要有以下2种：

1）具有井下-地面双向通信的大闭环控制系统。在大闭环控制系统中，由井下测量系统测得当前轨迹参数（井斜角、井斜方位角、井深坐标位置等），经脉冲信号传递给地面信息采集系统；信息采集系统将收集到的信号解码传达给地面控制中心，经计算机与设计轨道对比后，生成控制指令传达给井下控制系统；井下控制系统按预定程序算法计算出三支撑爪力，将指令传达给井下执行机构；通过液压使支撑爪支出，形成偏置合力，使得钻头按预定轨道钻进。

2）井下小闭环控制系统。在静态推靠式旋转导向工具中，外套是旋转的。国外现场经验表明，其旋转速度为1～2 r/h［11］。因此，井下测量系统需对支撑爪的位置α1进行实时监测。当α1的变化值Δα1大于某一规定值时，则井下控制系统需重新下达指令，使钻头继续按预定方向钻进［12］。

6　结论

1）旋转导向工具的井眼轨迹控制原理是实钻轨迹与设计轨道对比后确定一个目标逼近点，由当前钻进点按一定的全角变化率到达目标点。

2）静态推靠式旋转导向地面控制系统的下传指令是工作效率Ak和偏置合力αk。通过分析全角变化率与工作效率Ak的关系，以及井斜、方位变化率与偏置合力角αk的关系，分别给出了Ak和αk的算法。

3）将所得控制指令算法编入地面控制系统，应用结果表明，该控制指令算法精准，可实现360°全方位导向功能。

4）不同结构的旋转导向控制系统，地面控制指令算法不同。

［1］张绍槐.现代导向钻井技术的新进展及发展方向［J］.石油学报，2003，24（3）：82-85，89.

［2］付建民，韩雪银，马英文，等.vorteX型动力导向钻井系统在渤海油田的应用［J］.石油钻探技术，2014，42（3）：118-122.

［3］薛启龙，丁青山，黄蕾蕾.旋转导向钻井技术最新进展及发展趋势［J］.石油机械，2013，41（7）：1-6.

［4］杜建生，刘宝林，夏柏如.静态推靠式旋转导向系统三支撑掌偏置机构控制方案［J］.石油钻采工艺，2008，30（6）：5-10.

［5］程载斌，姜伟，蒋世全，等.旋转导向系统三翼肋偏置位移矢量控制方案［J］.石油学报，2010，31（4）：676-679，683.

［6］杨剑锋，张绍槐.旋转导向闭环钻井系统［J］.石油钻采工艺，2003，25 （1）：1-5，83.

［7］李琪，杜春文，张绍槐.旋转导向钻井轨迹控制理论及应用技术研究［J］.石油学报，2005，26（4）：97-101.

［8］李汉兴，蒋世全，李峰飞.旋转导向钻井工具空间姿态分析与测量方法研究［J］.中国海上油气，2013，25（6）：88-92.

［9］白家祉，苏义脑.井斜控制理论与实践［M］.北京：石油工业出版社，1990：315-317.

［10］郭宗禄，高德利，杨文强，等.下部钻具组合上切点的位置确定方法［J］.石油钻探技术，2014，42（2）：46-51.

［11］EDMONDSONJ，ABBOTTC，DALTONC，etal.Theapplicationofrotary closed-loop drilling technology to meet the challenges of complex wellbore trajectories in the Janice Field［R］.SPE 59218，2000.

［12］POLI S，DONATI F，OPPELT J，et al.Advanced tools for advanced wells：rotary closed loop drilling system-results of prototype field testing［J］.SPE Drilling&Completion，1998，13（2）：67-72.

（编辑赵卫红）

Control command algorithm of static push-the-bit rotary steerable system

WANG Yeqiang，LI Shibin，ZHANG Ligang，LI Chuang，XING Enhao，GUAN Bing
（College of Petroleum Engineering，Northeast Petroleum University，Daqing 163318，China）

Rotary steerable drilling system represents the highest level of directional drilling technology；however，the study of such technology is still in the primary stage in our country.Much effort should be done for this research.Based on the static push-the-bit rotary steerable system，the internal structures and the working principle，control command algorithm was researched.The drilling section is determined by planar circular arc curve；analyzing the angle of inclination，azimuth and total angular change rate，the right control commands for purposed drilling were realized.At the same time，a set of ground calculating software was developed；the experimental application shows that this method could calculate control commands accurately to implement guiding function.Finally a two-way communication closed-loop control chart of static push-the-bit rotary steering system is supplied for researchers to refer.

rotary steerable system；closed-loop system；planar circular arc curve；control commands；trajectory control

国家自然科学基金项目“基于应力-渗流-损伤多场耦合的清水压裂机理及储层筛选研究”（51274069）；东北石油大学青年自然科学基金“致密砂岩储层体积压裂应力场改造控制机理研究”（NEPUQN2014-26）

TE254

A

10.6056/dkyqt201602029

2015-08-17；改回日期：2016-01-07。

王业强，男，1991年生，在读硕士研究生，主要从事油气井工程理论和技术领域的研究工作。E-mail：fighter-wyq@qq. com。

引用格式：王业强，李士斌，张立刚，等.静态推靠式旋转导向控制指令算法［J］.断块油气田，2016，23（2）：261-264. WANG Yeqiang，LI Shibin，ZHANG Ligang，et al.Control command algorithm of static push-the-bit rotary steerable system［J］.Fault-Block Oil&Gas Field，2016，23（2）：261-264.