城镇土地定级中扩散因子衰减方法研究

任远辉，陈伟强，郭 雯，赵 洁，马月红

(河南农业大学资源与环境学院，河南 郑州 450002)

城镇土地定级中扩散因子衰减方法研究

任远辉，陈伟强，郭 雯，赵 洁，马月红

(河南农业大学资源与环境学院，河南 郑州 450002)

针对城镇土地定级中扩散性因子处理存在的问题，基于Dijkstra算法对最短路径衰减方法进行了改进，并以上街区住宅用地定级为实际应用案例，运用多因素综合评价法，在扩散因子处理上采用直线衰减和最短路径衰减两种方法获取结果，通过两种方法的对比，划分住宅用地定级范围，指出在土地定级中采用沿道路衰减，即最短路径衰减的合理性、客观性，并通过测算修正地价和两种方法的相关性系数，进一步说明沿道路衰减(最短路径衰减)在土地定级中应用的优越性、真实性。

城镇土地定级；住宅用地；道路衰减；路径成本；上街区

现行的城镇土地定级估价信息系统在对扩散性因素作用分值的计算中多采用直线衰减的方法，较少考虑路网分布条件对各类设施扩散作用的影响，而在现实中，道路两旁宗地的地价确实比远离道路的宗地地价高，较高级别的道路两侧宗地地价也比较低级别道路两侧地价要高，这也就决定了土地级别的高低是受道路扩展的影响的。研究扩散性因素作用分值沿道路衰减的分析方法，对客观真实反映定级因子分值有重要意义。中国的城镇土地定级方法主要采用多因素综合评价法和以价定级的方法，国内学者也对城镇土地定级的方法进行了广泛的研究、完善以及创新。郑光辉等[1]运用克里金插值的方法对土地级别进行了划分，王博等[2]在2013年时利用Voronoi图对贵阳市城镇土地进行了级别划分，高娟等[3]则基于遗传算法和支持向量机，对研究区域的城镇土地进行了定级，何伟等[4]采用以价定级的方法对四川南部县土地进行了分级研究。可见，国内学者多把目光聚焦在城镇土地定级的方法研究和模型创新上，对于定级过程中涉及的扩散因子的处理往往都还是遵照以往的处理方法，运用直线衰减，再在后期进行调整使其更接近实际。刘耀林等[5]曾基于Dijkstra算法引入最小路径，提出了最短路径衰减的概念，并以长春市为例进行了实际的应用，取得了良好的效果。花强等[6]以新沂市农用地定级估价对空间直线衰减、带通道表的桥扩散方法、最短到达时间扩散3种方法进行了对比分析。这些算法在实际应用中被证明得出的结果更优，更加符合现实情况，但由于方法的限制性和对技术人员的技术水平要求较高，所以在实际工作中应用性不强，在地方上没有很好的应用和开展。本研究定级方法上采用多因素综合评价法，但在扩散因子处理上采用路径衰减的方法，对之前的最短路径衰减进行了优化修改，在充分发挥ArcGIS在空间数据处理优越性的基础上，构建沿道路衰减的最短路径模型，最大程度符合真实的城镇内部的行走状态，最终确定研究区城镇土地的级别。

1 研究区概况

上街区位于北纬33°35′～34°40′，东经113°00′～113°30′，在郑州市区西38 km处，东西长5.25 km，南北宽3.75 km，东、西、北3面被荥阳市所包围，南与巩义市接壤。上街区面积64.7 km2。2013年底，上街区总人口13.5万人，其中城镇人口13.3万人。上街区多年平均降水653.8 mm，最高达1 048.5 mm，最低为400.6 mm，降水年内分布不均匀，降雨集中在夏季7、8月份。辖区没有长年地表河流湖泊，地下水是唯一的水资源。

上街区距郑州市中心38 km，陇海铁路、310国道由东向西横穿城区。全城区道路由南向北，主要有许昌路、中心路、济源路、厂前路、新安路、新乡路、上派路、安阳路等8条东西走向道路。由西向东主要有灵宝路、封丘路、洛宁路、孟津路、汝南路、登封路、淮阳路、新郑路等8条南北走向道路，基本形成纵横交错的道路网。

2 数据来源及研究方法

2.1数据来源

研究资料取自上街区2014年城镇土地级别与基准地价更新调整工作中的土地定级因素外业调查资料，具体包括具有扩散衰减影响特征的商服中心、道路、对外交通设施以及各类公共设施的相关数据。

2.2研究方法

各类定级因素对土地质量的影响一般为连续、渐变的，只有遇到河流阻隔、铁路分割、自然条件剧变等特殊情况时，才有可能造成土地质量的不连续分布。栅格数据模型在表示这种连续数据的变化上有明显优势，因此，上街区土地定级因素作用分值的计算拟通过构建栅格数据模型，采用多因素综合评价法进行城镇土地定级。多因素综合评价法综合考虑经济、非经济等各个方面的因素，并采用定性与定量相结合，科学标准化指标，把复杂的对事物的总体判断转化为对事物某些方面的单项判断，避免了主观随意性，保证了土地级别的统一性。在土地级别划分结束后，再对其结果进行相关性分析，进而保证定级划分的准确性。

在对扩散因子的处理上，本研究采用沿道路衰减的方法进行数据处理。在实际考察中，地价往往受道路影响较大，道路两侧的宗地地价往往比不临道路的宗地地价高，同是临街的宗地，通达度较好的道路两侧地价比通达度不好的道路两侧地价要高。这个现象在商业、住宅等用地类型中表现的最为明显。城市交通发达的地区，交通时间价值就越高，这是城市交通系统对土地价格产生影响的最根本原因[7]。

城镇道路按照可利用性划分一般有主干道、次干道、辅路或者支路3类，其中主干道和次干道又可以分为混合型主次干道、生活性主次干道等等。在实际生活中，各类衰减因子往往都是沿道路进行不同程度的扩散。由于道路自身因素的限制，不同道路上所能达到的速度是不一样的，从而交通时间价值也就有了区别。最短路径衰减的方法便是依据这个原理，首先将在某一段道路内的行走看作一个固定值，按照不同级别道路的时间、速度成本标准化出一个属于不同级别道路的权重代表道路行走的固定值，由定级范围内所有点到达扩散因子的最短成本即是所求的最短路径。

算法上，本研究以Dijkstra算法为基础，这也是目前最短路径中采用最多的一种算法。其基本思想是按路径长度递增的顺序逐步产生最小路径的方法[5]。具体到扩散因子衰减而言，最初形态上，定级区范围分为2部分，一部分是扩散因子所在区域，假设为A，可以是点或者面，另一部分是定级区其他所有以栅格形式表现的集合，假设为B。随后，以A为中心，从B集合中不断寻找单个栅格到达A区域最短的栅格成本路径，最后实现B集合所有栅格全部找到去A区域的最短路径，所得结果即是该扩散因子的最短路径衰减结果。

3 结果与分析

3.1最短路径模型构建

为了解决向量数据无法附带属性的问题，本次定级将研究范围区划分为20 m×20 m的栅格，栅格内为均质环境。每一个栅格赋予一个定值，代表在该栅格内的行走距离，或交通时间价值。因此，根据这一理念，为体现出道路通达性对定级结果的影响，参照上街区道路级别划分，通过赋予不同的栅格不同的行走距离值来反映在不同级别道路上的行走阻力。赋值越小，代表在该栅格内行走阻力越小，即行走越通畅，赋值越大，代表在该栅格内行走阻力越大，最终的最短路径即为沿道路栅格行走到达某一点的最短行走总距离。结合上街区实际情况，本研究将在大于宽度40 m的主干道上行走的分值赋值为1分，其余道路上行走的分值赋值为2分，无道路地区赋值为4分，不能行走的区域，如铁路、河流不赋值，即代表无法行走，将直接绕过寻找最短绕行路径。最后生成tiff格式文件，做出模型，如图1。

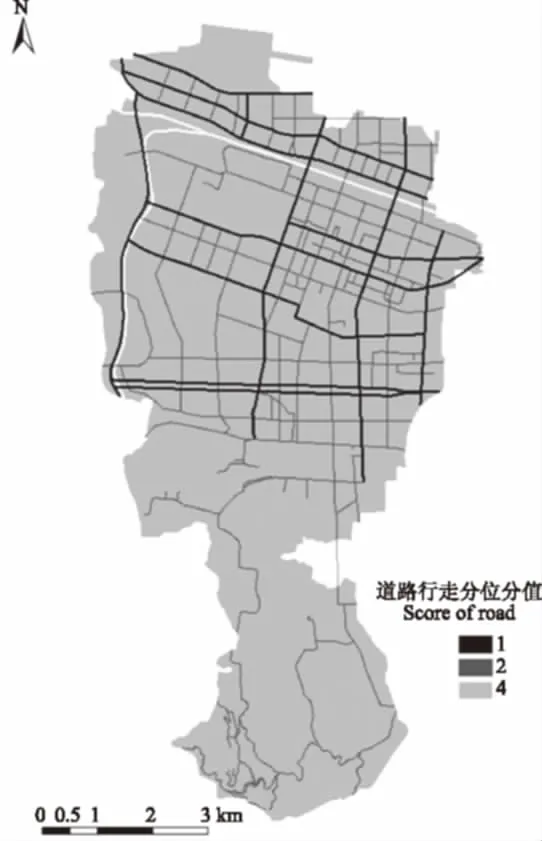
图1 最短路径成本模型Fig.1 Shortest path cost model

3.2扩散性因子衰减方法对比

在计算评价单元的路径成本距离时，本研究使用的是ArcGIS的成本距离加权函数法(Cost-Weighted Distance)，记录从任意单元出发，沿着最小成本路径，到达最近源的路径。商服繁华度是人们在选择住宅区时的一个重要的考虑因素，以商服繁华影响度为例，商服繁华度的直线距离衰减因素作用分值图，如图2，最短路径成本衰减作用分值图，如图3。从2个图的比较中可明显看出，商服中心的直线距离衰减网格分值的等值线图为一个同心圆，不受现状道路网络的影响，边缘光滑，扩散均匀。而商服繁华度的最短路径衰减因素作用分值图则与直线距离衰减明显不同，其网格分值分布状况受现状道路网络和障碍地物的影响，充分反映了城镇土地质量变化的客观实际，符合人们在行走过程中的情况。

图2 商服中心直线距离衰减图Fig.2 The linear distance decay diagram of commercial centers

图3 考虑最短路径的商服中心成本距离衰减图Fig.3 The cost distance decay chart considering the shortest path of the commercial centers

以道路通达度因子为例，直线距离衰减因素作用分值图如图4所示，最短路径衰减因素作用分值图如图5所示。从2个图的比较中可明显看出，在不考虑路径成本的情况下，扩散性因子分值扩散幅度过大，扩散边缘呈平滑圆角趋势，没有图5层次分明，道路通达度的最短成本路径衰减因素作用分值图则与直线距离衰减明显不同，作用分值沿道路延伸，印证了商服繁华度中2种方法比较体现出的差异。

图4 道路直线距离衰减分值图Fig.4 The linear distance decay diagram of roads

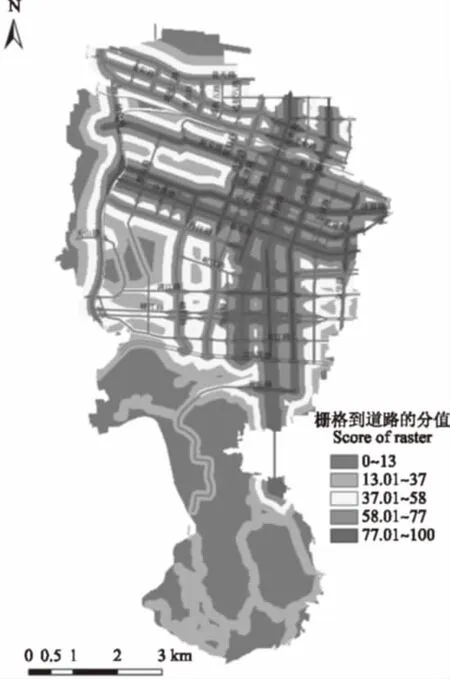
图5 考虑最短路径的道路成本距离衰减分值图Fig.5 The roads cost distance decay chart considering the shortest path

3.32种方法定级结果对比

以上街区住宅用地定级为例，运用多因素综合评定法(公式如下)，对比2种距离计算方法所得分值的差异，结果如图6、图7所示。从图6和图7可以看出，2个计算结果分值区间大体一致，扩散总体趋势都是以一级商服中心为中心，向四周扩散。直线距离衰减的结果中，2级区域沿新安路向西扩散较深，区域形状较成本距离衰减平整规则，而考虑道路可达性的成本距离衰减的结果中，沿新安路往西扩散趋势小于直线衰减，但向西南、南部和北部的扩散趋势要较直线衰减更明显，较高的分值区域均沿道路分布，突出了道路对定级结果的影响作用。

式中：Sf为结果总分值；k为定级因素(因子)数目；pk为各定级因素对单元的作用分；fk为各定级因素权重。

图6 直线衰减的上街区住宅用地定级分值图Fig.6 The Shangjie District residential land grading score chart using the linear attenuation

图7 使用最短路径的上街区住宅用地定级分值图Fig.7 The Shangjie District residential land grading score chart using the shortest path

对比2种距离计算方法所得分值的频率直方图，如图8、图9，直线衰减的频率分值在13.84～92.66之间，在13.84～21.88出现1次较大波峰，分值起伏明显，基于路径成本的频率分值在13.49～93.09之间，在13.49～22.86出现1次较大的波峰，22.86～47.83分值稳定，体现出更好的可控性，其大体趋势较前者更稳定。

图8 直线衰减的频率直方图Fig.8 Frequency histogram of linear attenuation

图9 最短路径的频率直方图Fig.9 Frequency histogram of shortest path

通过SPSS21.0的变量相关性分析的功能，将收集到的182个地价样点修正后和2种衰减方法得到的定级分值做相关性分析，结果如表1所示。

从表1可以看出，路径成本定级得出的结果和地价的相关性系数是0.82，达到了极显著相关，高于直线衰减定级分和地价的相关性0.77，说明路径成本定级方法要优于直线衰减。

表1 2种定级方法和地价的相关性分析Table 1 Correlation analysis of two kinds of gradation method and land price

4 结论与讨论

传统的扩散性因子衰减处理在方法上是将定级范围内部看作一个均质的空间，除了具有阻隔因素的铁路、河流水域以外，在空间内所有区域行走的时间成本是一样的，通过和地价样点的相关性分析可以看出，通过传统直线衰减方法做出的定级区域和地价的分布是呈现出一定相关性的，这表示直线衰减有它的合理性。

基于道路分级的路径成本衰减方法在传统的直线衰减方法上进行修改提升，突出了定级范围内不同道路级别对于人们行走时间成本的影响，即定级区域内的不均质性和人们的主观选择性，对定级分值的计算更加严密合理。通过和地价样点的相关性分析，路径成本衰减和地价样点呈显著相关，并且和直线衰减也具有相关性，表明该方法在传统方法的基础上划分城镇土地级别更加合理和准确，在定级结果上更加符合实际情况。当然，在采用此方法进行城镇土地定级的时候，依照不同地方的实际情况，在最短路径模型构建时，其交通时间价值的成本赋值也是可以进行讨论的。综上所述，在城镇定级过程中，采用基于路径成本的衰减方法得到的土地定级结果更符合实际情况，效果也较传统方法更优。

本研究在基于传统直线衰减处理定级因子的基础上进行了改进，将最短路径衰减的方法应用到了城镇土地定级的过程中，并指出了传统直线衰减的不足和最短路径衰减的合理性，证明了将最短路径衰减的方法应用于实际工作的客观性，实现了对现实情况的有效反映。同时，最短路径衰减法和传统的直线衰减相关性高，可实现性好，是对传统方法的改良而不是推翻重来，有较强的可操作性。通过实例分析，将两种方法应用于实践，用实际数据进行对比分析，用结果进一步说明了将最短路径衰减方法应用于城镇土地定级工作的优越性和有效性。

[1] 郑光辉，黄克龙，张志宏，等．运用克里金空间插值技术进行土地级别划分[J]．南京师大学报(自然科学版)，2007，30(1)：112-116.

[2] 王博，符海月．基于Voronoi图的贵阳市城镇土地定级[J]．中国土地科学，2013，27(4)：80-90.

[3] 高娟，王海军，张怡然，等．基于遗传算法和支持向量机的城镇土地定级方法研究[J]．华中师范大学学报(自然科学版)，2014，48(6)：917-922.

[4] 何伟，唐琴．城镇土地以价定级方法研究——以四川省南部县为例[J]．四川师范大学学报(自然科学版)，2012，35(5)：694-698.

[5] 刘耀林，范延平，唐旭．最短路径方法在土地定级中的应用[J]．武汉测绘科技大学学报，2000，25(6)：510-515.

[6] 花强，都金康，李谦．土地定级中定级因子扩散算法研究[J]．南京大学学报(自然科学版)，2006，42(6)：636-642.

[7] 吴次芳，宋戈．土地利用学[M]．北京：科学出版社，2009：382.

(责任编辑：朱秀英)

Studyonthemethodofdiffusionfactorinurbanlandgrading

REN Yuanhui，CHEN Weiqiang，GUO Wen，ZHAO Jie,MA Yuehong

(College of Resource and Environment，Henan Agricultural University，Zhengzhou 450002，China)

In view of the existing problems in urban land grading,this study selected Shangjie District of Zhengzhou City as the study area,and used the method of multi factor comprehensive appraisal to improve the shortest path attenuation method based on the Dijkstra algorithm and used both linear attenuation and the shortest path attenuation to manage the diffusion factor.By the comparison of linear attenuation and the shortest path attenuation and the division scope of residential land grading,the result shows that the shortest path attenuation with rationality and objectivity along the road is used in land gradation.By calculating the correlation coefficient between linear attenuation and the shortest path attenuation and revising the land price,the paper further illustrates the advantages and the reality of the application of the shortest path attenuation in land grading.

urban land grading; residential land; road attenuation; path cost; Shangjie District

F301.23

：A

1000-2340(2016)03-0411-05