基于改进群搜索优化算法的变差函数拟合
2016-09-23张艺丹葛新民
陈 华, 张艺丹, 葛新民
(中国石油大学(华东) a. 理学院;b.地球科学与技术学院,青岛 266580)
基于改进群搜索优化算法的变差函数拟合
陈华a, 张艺丹a, 葛新民b
(中国石油大学(华东) a. 理学院;b.地球科学与技术学院,青岛266580)
群搜索优化算法是一种群智能优化算法,通过研究群搜索优化算法的优劣以及其改进的方法,并将改进的群搜索优化算法应用于变差函数的高斯、指数和一阶及多阶球状模型的最优拟合。实例表明,群搜索优化算法能够有效地应用于变差函数拟合。
群搜索优化算法; 变差函数; 地质统计学
0 引言
在地质统计学中,作为最基本和最重要的模拟工具——变差函数,它是一种矩估计方法,用于表现数据值的空间互相关性,数据点在空间上距离越相近,相关性就越大。在地质统计模拟中,变差函数最优拟合实质是对给定样本的数值处理得到相应区域的解析函数。变差函数的拟合有很多方法,比如在指定出变差函数模型后,可以使用最小二乘法[1]、加权回归多项式[2]、遗传算法、粒子群优化算法[3]等进行拟合。然而这些方法都存在不同方面的问题,最小二乘法和加权回归多项式方法需要手动拟合,费时费力,存在一定的人为因素,缺乏统一客观的标准,而且加权回归多项式算法所计算得到的参数存在正负号问题,使得函数在拟合时无法得到最优解。遗传算法和粒子群算法虽然在一定程度上解决了自动拟合问题,但在实现过程中,参数较多,结构复杂,对执行速度产生影响。这里采用基于群搜索优化算法的变差函数最优拟合,克服了上面所存在的问题,能够有效的对地质数据进行变差函数拟合。
群搜索优化算法源于动物搜索行为和种群理论,它是由S.He等[4]提出的一种群智能优化算法[4],该算法基于Producer-Scrounger模型[5](PS模型)。在群搜索优化中,种群中有三类成员:①发现者(生产者);②追随者(参与者);③游荡者。搜索到最丰富资源并共享资源的群成员为发现者,从发现者获取资源信息并掠夺资源的群成员为追随者,兼有发现者和追随者角色的群成员为游荡者,个体在整个搜索过程中三个角色是可以相互切换的,是随机的。基于群搜索优化算法对求解多峰函数优化问题具有明显优势,从而对变差函数进行最优拟合比较有效。
1 基于变差函数模型的适应函数
为了使群搜索优化算法更好应用于变差函数[6-8]的高斯、指数和一阶及多阶球状模型的最优拟合,定义适应函数如式(1)所示。
(1)
其中:F(i)为第i个位置个体的适应度;hj为变差函数的第j个滞后距;γ(hj)为第j个理论模型对应的变差函数值;γ*(hj)为第j个滞后距对应的实验变差函数值。
1)球状模型。
一阶球状模型的适应函数:
(2)
二阶套合球状模型的适应函数:
(3)
2)指数模型。
(4)
3)高斯模型。
(5)
2 基于预测因子的群搜索优化算法
群搜索优化算法(GSO)是最近几年新出现的智能优化算法,已广泛地应用于实际生活中各种求解的最优化问题,尤其是在求解连续多维函数的最优化问题。但是在求解高维函数优化问题时,各维之间的相互作用会对其局部求解能力产生影响,导致它的精确度下降,而且群搜索优化算法(GSO)在使用PS模型时候选解具有强烈的趋向性,使算法中选择的发现者有可能一直保持不变,降低了算法的空间搜寻能力。引进带有趋势的预测因子,可使群搜索优化算法[9-10]在一定程度上解决或减少这些问题,从而有效应用于变差函数拟合。
2.1改进群搜索算法的基本原理
在带预测因子的群搜索优化算法中,预测因子是在迭代过程中各成员保存记录发现者的移动方向作为经验,以此预测估计下一个发现者的位置。为了使其具有多样性,只随机选取少数的群成员个体来记录每一次的移动的方向及距离。改进的群搜索优化算法即保持原来高维优势,同时又在低维优化问题的性能上有了很大程度上的提高,并且计算的过程得到了简化,运算的速度明显加快。
带有预测因子的群搜索算法:
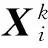
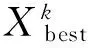
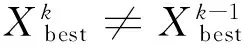
(6)
(7)
其中:r1、r2为n维向量且其各分量是0到1之间的均匀随机数;c1、c2为常系数。
剩余群成员中,再随机选择80%的成员作为追随者,再随机产生一固定步长,追随者以这个步长靠近发现者:
(8)
式(8)中,r3为n维向量且其各分量都为0到1之间的均匀随机数。
最终剩余的群成员都作为游荡者,可以任意方向的随机移动指定的距离:
(9)式中:r4为n维向量且其分量都是标准正态分布的随机变量;h为n维向量,步长常量;mutationflag为n维向量,是个用[0,1]表示的布尔值向量,标志了各维是否允许变异,用以下方法可得:
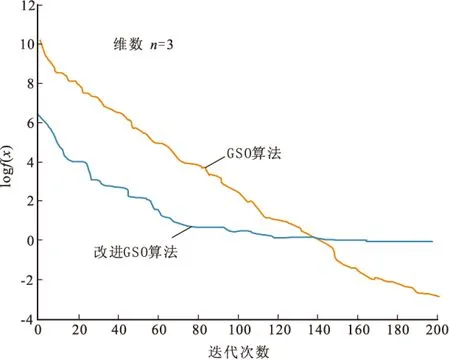
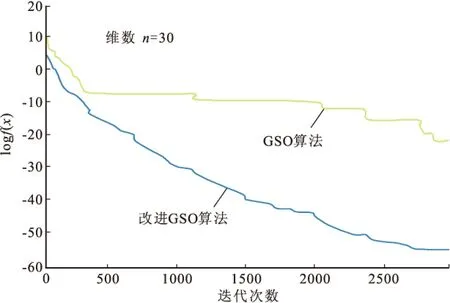
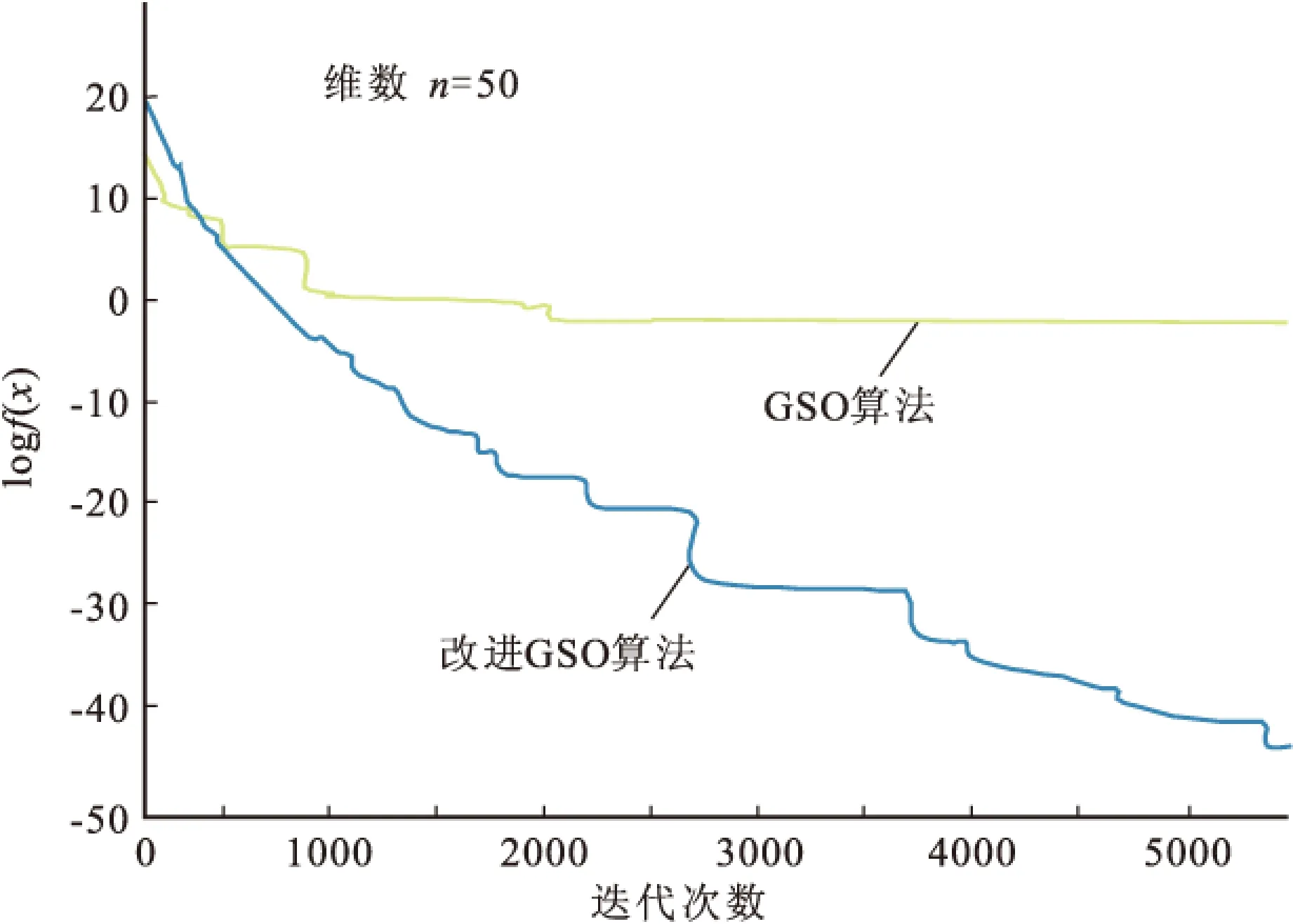
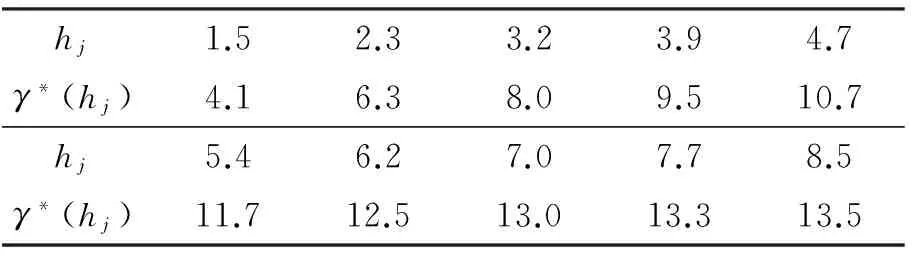
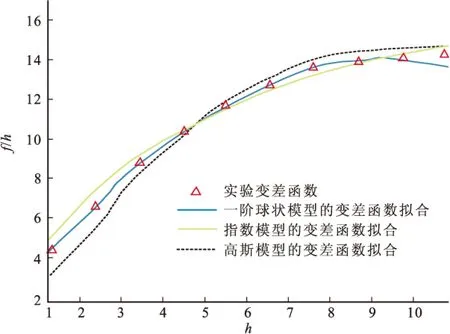
mutationflag=r5 (10) 式(10)中,r5为n维均匀分布随机向量。 (11) 式(11)为分量变异率,其值随着迭代次数的增加而递减,<运算符为比较符号的左边每个分量与右边标量的大小,返回的是用0、1表示布尔值。 根据上述算法原理,改进群搜索算法的流程图见图1。 图1 改进群搜索算法的流程图Fig.1 The flow chart of the improved GSO 2.2数值实验 为了更有效地测试算法应用于变差函数拟合的有效性,选择BenchMark测试函数集中的Sphere函数: (11) 比较GSO算法和改进的GSO算法: 1)当测试函数中的n=3时,两算法的执行情况见图2。从图2中看出当n=3时,改进的基于群搜索优化算法并没有多少优势,而且在迭代到140之前,都是处于劣势的。 图2 GSO和改进的GSO算法执行情况1Fig.2 The first implement situation of GSO and the improved GSO 图3 GSO和改进的GSO算法执行情况2Fig.3 The second implement situation of GSO and the improved GSO 2)当测试函数中的n=30时,两算法的执行情况见图3。从图3可以看出,当n=30时,改进的基于群搜索优化算法优势明显,相比较基于群搜索优化算法,其能在更少的时间里达到更好的效果。 3)当测试函数中的n=50时,两算法的执行情况见图4。从图3、图4中可以看出,当n=50时,改进的基于群搜索优化算法的优势明显。 由以上分析可知,改进的基于群搜索优化算法在低维情况下,优势不明显或者没有优势,其收敛的速度,计算精度都比基于群搜索优化算法的差。高维情况下,改进的基于群搜索优化算法的收敛速度和计算精度比基于群搜索优化算法具有显著优势。 图4 GSO和改进的GSO算法执行情况3Fig.4 The second implement situation of GSO and the improved GSO 2.3实例计算 根据文献[7],对江西某矿B矿体垂直方向钼品位的实验变差函数值γ*(hj)进行拟合。实验数据见表1 。 表1 B矿体垂直方向钼品位的实验变差函数数值表 通过不同变差函数模型进行拟合,比较其优劣。根据表1的实验变差函数值,可以确定待拟合参数的取值范围,分别是c0=[0,2]、c=[0,20]、a=[2,10]。为了更真实的记录算法结果,减少偶然性,此算法的结果都是运行50次取的平均值。 将带有预测因子的群搜索优化算法应用于上述例子,得到了变差函数的三种模型最优拟合结果。如图5所示,球状模型的变差函数拟合效果最好,即与实验数据吻合的最好。 图5 改进GSO算法变差函数的三种模型最优拟合Fig.5 The optimum fitting of three models of function of variation of the improved GSO 从传统变差函数的拟合方法的优缺点出发,提出了基于改进群搜索算法的变差函数拟合,在保证其最优拟合的情况下,提高了收敛的速度和计算的精度。实验结果表明,它能够更有效地解决变差函数拟合问题,且拟合效果良好。 [1]CRESSIE N.Fitting variogram models by eighted least squares[J].MathvGeol,1985,17:563-567. [2]MARDIA K V,MARSHALL R J.Maximum ikelihood parameter estimation of models orresidual covariance in spatial regression[J].Biometrika,1984,71:135-138. [3]矫希国,刘超.变差函数的参数模拟[J].物探化探计算技术,1996,16(2):157-161. JIAO X G,LIU C.Estimation of variation parameter[J].Computing techniques for giophysical and geochemical exploration,1996,16(2):157-161.(In Chinese) [4]HE S,WU Q H,SAUNDERS J R.A novel group search optimizer inspired by animal behavioral ecology[C].In:Proceedings of 2006 IEEE Congress on Evolutionary Computation,vancouver,BC,Canada,2006:16-21. [5]C.J.BARNARD,R.M.SIBLY.Producers and scroun-gers:a general model and its applica-tion to captive flocks of house sparrows[J].Animal Behaviour,1981,29:543-550. [6]刘爱利,王培法,丁园圆.地统计学概论[M].北京:科学出版社,2012. LIU A L,WANG P F,DING Y Y.Conspectus of geo-statistics[M].Beijing:Science press,2012.(In Chinese) [7]梁昔明,肖晓芳.基于PSO算法的变差函数球状模型参数拟合[J].计算机工程,2011,37(14):155-157. LIANG X M,XIAO X F.Parameter fitting of variogram spherical model based on particle swarm optimization algorithm[J].Computer Engineering,2011,37(14):155-157.(In Chinese) [8]陈学工,陈婷,肖晓芳.混沌粒子群算法自动拟合理论变差函数[J],计算机工程与应用,2012,48(4):37-39. CHEN X G,CHEN T,XIAO X F.Chaos particle swarm optimization algorithm to match theoretical variogram automatically.Computer Engineering and Applications,2012,48(4):37-39.(In Chinese) [9]张雯雰,刘华艳.改进的群搜索优化算法在MATLAB中的实现[J].电脑与信息技术,2010,18(3):44-46. ZHANG W F,LIU H Y.MATLAB implementation of the improved group search optimizer algorithm[A].Computer and Information Technology,2010,18(3):44-46.(In Chinese) [10]张雯雰,滕少华,李丽娟.改进的群搜索优化算法[J].计算机工程与应用,2009,45(4):45-51. ZHANG W F,TENG S H,Li L J.Improved Group Search Optimizer algorithm[J].Computer Engineering and Applications,2009,45(4):45-51.(In Chinese) The optimal fit of the variational function based on improved group search optimizer algorithm CHEN Huaa, ZHANG Yi-dana, GE Xin-minb (1.College of Science, China University of Petroleum (East China), Qingdao266580, China;2.School of Geosciences, China University of Petroleum (East China), Qingdao266580, China) Group search optimizer algorithm is a new method swarm intelligence introduced by S. He and Q.H.Wu in 2006. By studying on the advantages of group search optimizer algorithm and its improved methods, the improved group search optimizer algorithm is applied to the variational function based on the Gaussian model, the exponential model, the first spherical model and multistage spherical model. Examples show that the group search optimizer algorithm can be effectively applied to the optimal fit of the variational function. group search algorithm; the variational function; geostatistics 2015-05-02改回日期:2015-07-22 国家自然科学基金(41474100);山东省自然科学基金(ZR2013DM015,ZR2014DQ007) 陈华(1972-),男,副教授,主要研究方向为工业应用数学,E-mail: delaunay@163.com。 1001-1749(2016)04-0566-05 P 631 A 10.3969/j.issn.1001-1749.2016.04.20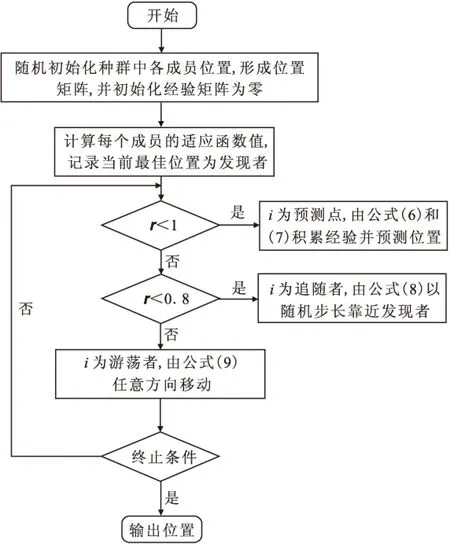
3 结论
