冷弯C型钢梁在双向弯曲情况下的屈曲模态分析

李相超,万红霞

(武汉理工大学 土木工程与建筑学院，湖北 武汉 430000)



冷弯C型钢梁在双向弯曲情况下的屈曲模态分析

李相超,万红霞

(武汉理工大学 土木工程与建筑学院，湖北 武汉 430000)

屈曲模态在一定程度上影响了冷弯C型钢梁构件的受力性能，为了得到钢梁屈曲模态和双向弯曲之间的联系，采用ANSYS有限元软件，建立SHELl181壳单元有限元模型，对冷弯C型钢梁在双向弯曲作用下的失稳进行了分析，得到钢梁在不同角度的斜向横向力作用下的不同屈曲模态，并对双向受弯钢梁屈曲模态的一般规律进行总结。

冷弯C型钢梁；双向弯曲；有限元；屈曲模态

冷弯型钢在国内外发展迅速，应用广泛。关于冷弯C型钢梁，国内外学者做了大量实验和理论研究，但关于它在双向弯曲情况下的研究尚属空白，而这种受力情况在实际应用中是可能存在的。采用大型有限元软件ANSYS建立有限元模型，考虑不同角度的斜向横向荷载作用，利用荷载等效的方式模拟双向弯曲的冷弯C型钢梁受力情况，进行特征值屈曲分析，得到不同角度斜向横向荷载作用下钢梁不同的屈曲模态，迅速并结合不同角度斜向横向荷载作用时钢梁的截面应力分布，得到双向弯曲作用下冷弯C型钢梁屈曲模态的一般规律。

1　冷弯薄壁型钢

1.1冷弯薄壁型钢的特点和应用

冷弯薄壁型钢是由一定厚度的钢板或钢带在常温下弯曲成型的，钢板或钢带的厚度通常都为0.4～6.4 mm[1]，作为钢构件中的后起之秀，它有着明显的优势：(1)成型设备技术要求不高，制作加工简单，便于量产和推广；(2)冷成型加工可以得到灵活多变的截面类型，选择最经济的强度重量比；(3)自重轻，有着较好的抗震性能，并且环保节约美观；(4)冷弯型钢结构建筑，屋面墙面构件与主体钢架连接可靠牢固，有较强的蒙皮效应，减小构件受力和变形；(5)包装运输方便，安装快捷，施工周期短，可回收利用。这些优点迎合了对保温、防火、防水、抗震、隔音和环保经济等技术指标要求愈加苛刻的现代建筑，使之快速发展。

不只是建筑业，汽车、飞机、运输业等都成了冷弯型钢的用户[2]，冷弯型钢在钢铁业中占的比重越来越大。在一些发达国家，高达60%的冷弯型钢用于建筑业中[3]，形成成熟的设计使用体系，现阶段开始向材料高强度，截面复杂化，组合多样化发展。

1.2冷弯薄壁型钢的失稳形式

钢结构及构件稳定问题一直是研究人员的焦点，冷弯薄壁型钢因为延性较低，板件更薄，截面更复杂，其失效方式基本上都是失稳破坏，稳定问题的重要性不言自明，也是各国冷弯型钢设计规范编制的重点。

冷弯薄壁型钢的失稳方式有三种[4]。第一是构件的整体失稳，包括扭转失稳，弯曲失稳和弯扭失稳。整体失稳是相对构件而言，截面不发生改变，只有相对位移或者转角，构件屈曲时的半波长最长，且与荷载形式和边界条件有关，对初始缺陷有较明显的影响，屈曲后强度增加不大。第二是板件的局部失稳，顾名思义，这是涉及板件的局部屈曲，板件往往会呈现凹凸不平的波段，但是板件之间的连接线，保持着原来的直线，截面的轮廓形状没有变化，一般而言，局部屈曲的半波长度都较短，这和宽厚比较大的薄板抗弯强度不大有着密切关系。值得一提的是，由于板件的横向薄膜效应和屈曲后的内力重分布，形成板件的后屈曲强度，并不易受板件本身缺陷影响。构件宽厚比和局部屈曲有着直接的联系，热轧型钢通过限制宽厚比和在构件敏感部位设置加劲肋来控制局部屈曲。但这并不适用于冷弯型钢，其一，冷弯薄壁钢构件的设计出于经济的考虑往往使用更少的钢材，其二，冷弯型钢被要求有着更好的抗弯抗扭性能，这就必然使得截面分布尽量远离形心，所以实际上要求更薄的板件分布在更大的范围。宽厚比达不到要求，为限制局部屈曲，冷弯型钢构件往往在截面设置褶皱，大量实验证明，复杂截面的冷弯型钢构件可有效避免局部屈曲。

图1　CUFSM生成的屈曲模态图

上述两种失稳类型人们认识较早，大量实验研究形成了较成熟的理论，直到1978年，澳洲学者Hancock[5]提出了畸变屈曲(Distortional)的概念，这才引起业界关注和重视。畸变屈曲是区别于整体屈曲和局部屈曲的第三种屈曲模式，其本质原因是边缘窄边没有起到足够地加劲作用，致使受压翼缘绕翼缘和腹板的连接线发生转动。屈曲时截面形状产生畸变，轮廓尺寸变化，不再符合刚周边假定，畸变屈曲的半波长度适中，介于前两者之间。相较局部屈曲，畸变屈曲缺陷敏感性高，易受构件几何缺陷影响，屈曲后强度增幅很小，大大降低了构件承载能力，故而成为冷弯薄壁型钢的研究重点和稳定设计重要的控制条件。图1由线条软件CUFSM[6]生成的冷弯薄壁C型钢构件三种不同屈曲模式的截面变形图。

图2　冷弯C型钢梁截面

由图1(a)可以看出，截面形状没有变化，只发生了刚性位移，是整体屈曲；图1(b)板件交线维持不变，之间的板件发生了鼓曲，是典型的局部屈曲变形图；图1(c)和图1(d)分别是受压和受弯两种情况下的变形图，两者大同小异，卷边和翼缘共同绕着腹板和翼缘的交线发生转动变形，构件截面发生变化，卷边和翼缘的交线也发生不同程度的弯曲，两者都是畸变屈曲。

2　冷弯C型钢受弯时的受力分析

承受无偏心横向荷载作用的钢梁主要按照受弯和受剪承载力设计，构件上存在弯曲正应力和弯曲剪应力，在ANSYS屈曲分析中，只考虑构件的线弹性阶段，在材料力学中，我们知道构件截面边缘的最大应力为：

σ=Mx/Wnx

(1)

当横向荷载作用力与钢梁截面x轴夹角为0°，90°和180°时，冷弯C型钢梁截面正应力分布图分别如图3所示,其中“+”为压应力，“-”为拉应力。

图3　钢梁弯曲正应力

图4　应力-应变关系曲线

3　冷弯C型钢梁有限元模型

采用ANSYS有限元软件，进行冷弯C型钢梁在双向弯曲作用下的屈曲分析，采用shell181壳单元建立有限元模型。选择碳素结构钢Q235作为研究的材料依据，钢材弹性模量取E=2.06×105N/mm2，屈服强度为fy=235 N/mm2，泊松比v取0.3，按照理想的弹塑性材料来定义应力-应变曲线，如图所示，在定义材料的非线性时，采用Von Mises屈服准则和相应的Mises流动法则以及双线性等向强化模型材料模型。

考虑到冷弯C型钢梁的双向受弯，荷载与主轴方向是倾斜的，在模型上施加荷载时，将横向荷载按照x和y轴方向分解，x轴方向上的荷载平均在腹板的节点上，而y轴方向上的力，平移到腹板中间，根据力的等效原理，需增加一对作用在上下翼缘的力偶，力偶大小由腹板高度和腹板与y轴方向上分力的距离决定。横向荷载等效简化如图5所示。

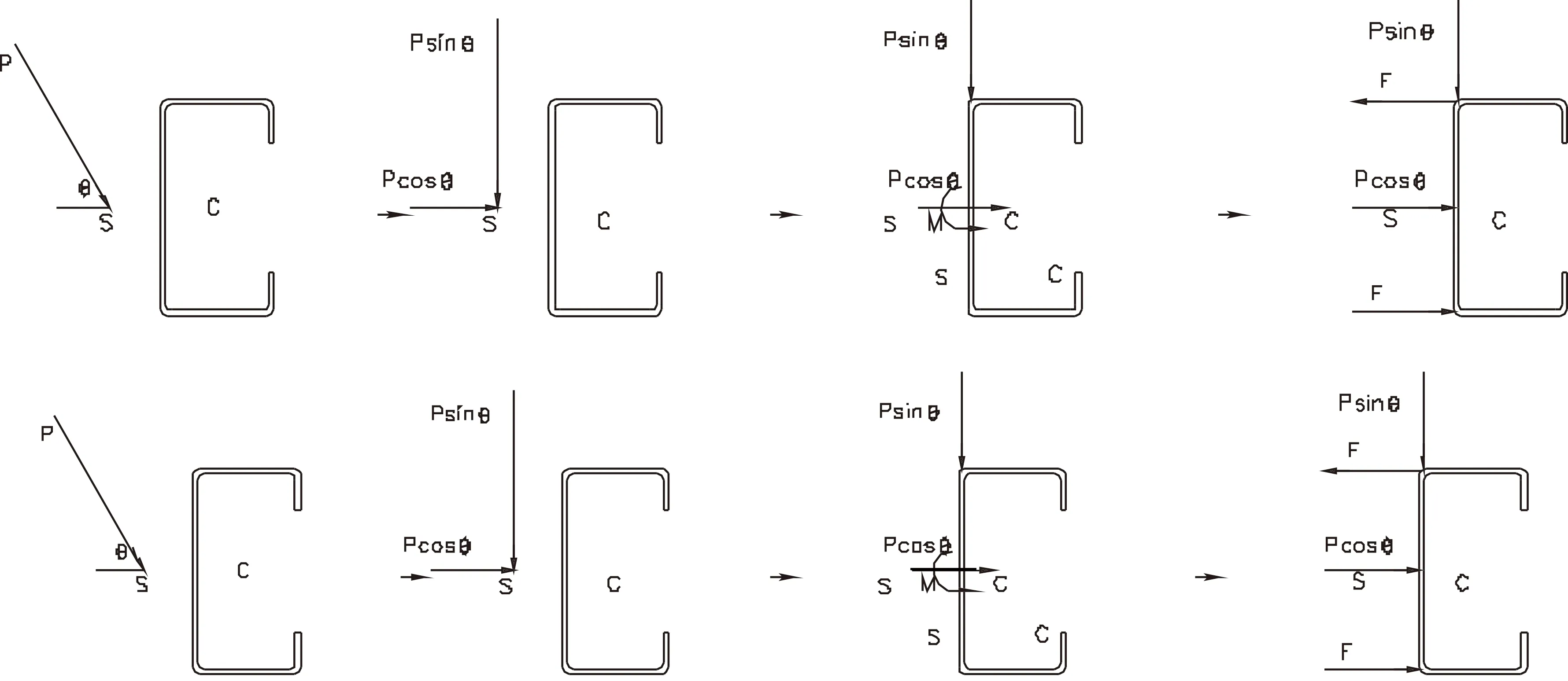
图5　横向荷载简化

4　冷弯C型钢双向受弯时的屈曲模态

选取H80B40C15T2截面的冷弯C型钢梁，有L=1 000 mm，L=1 500 mm和L=2 000 mm三种跨度，横向集中荷载与构建截面x轴夹角从0°到180°共13组不同角度的情况见表1：

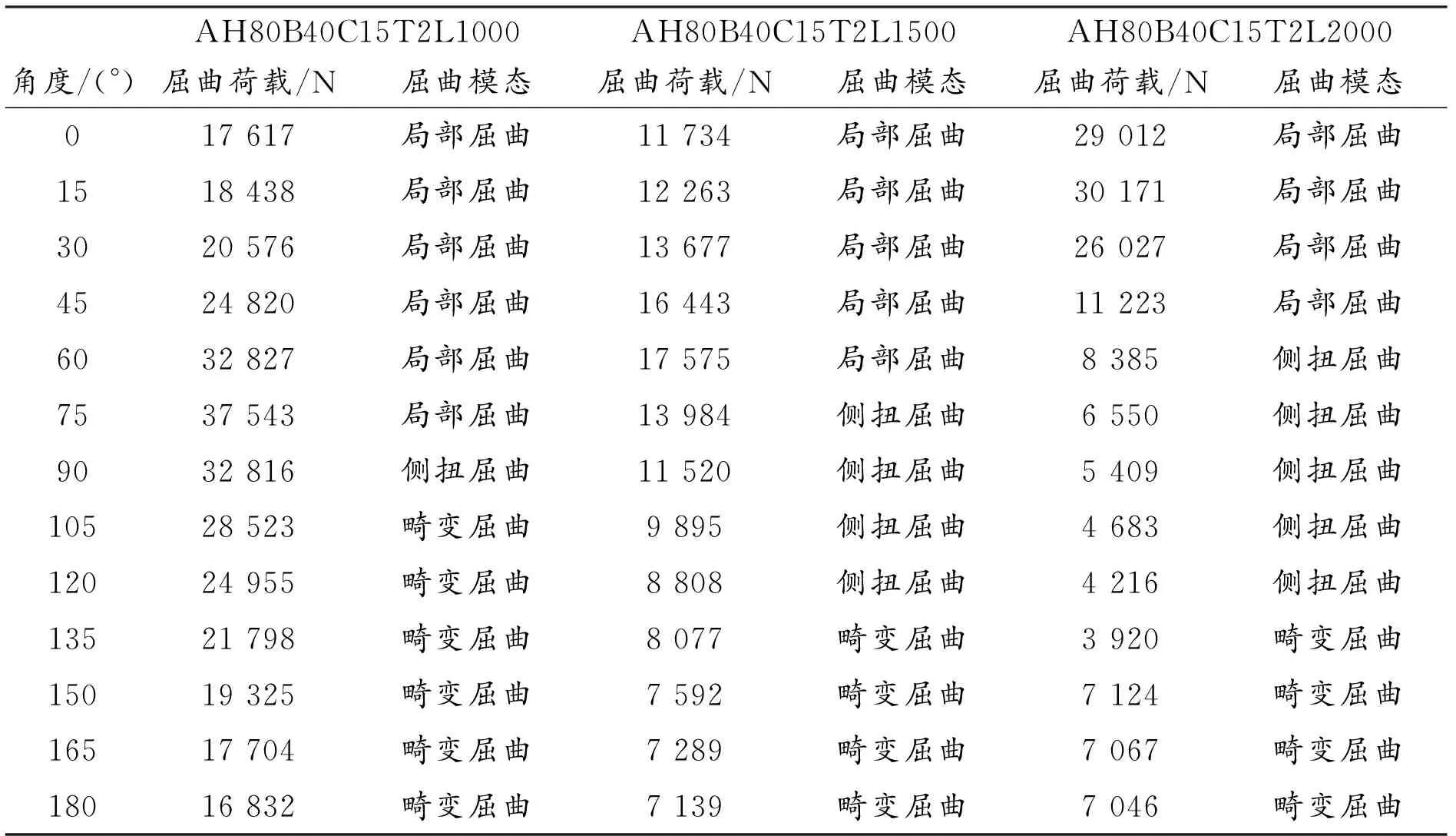
表1　H80B40C15T2集中荷载屈曲分析

在跨长L=1 000 mm的构件中，从0°到75°六组数据中，全部表现出了局部屈曲模态，而且屈曲的程度也大不相同, 从z轴观察0°到75°的屈曲模态图如图6所示。

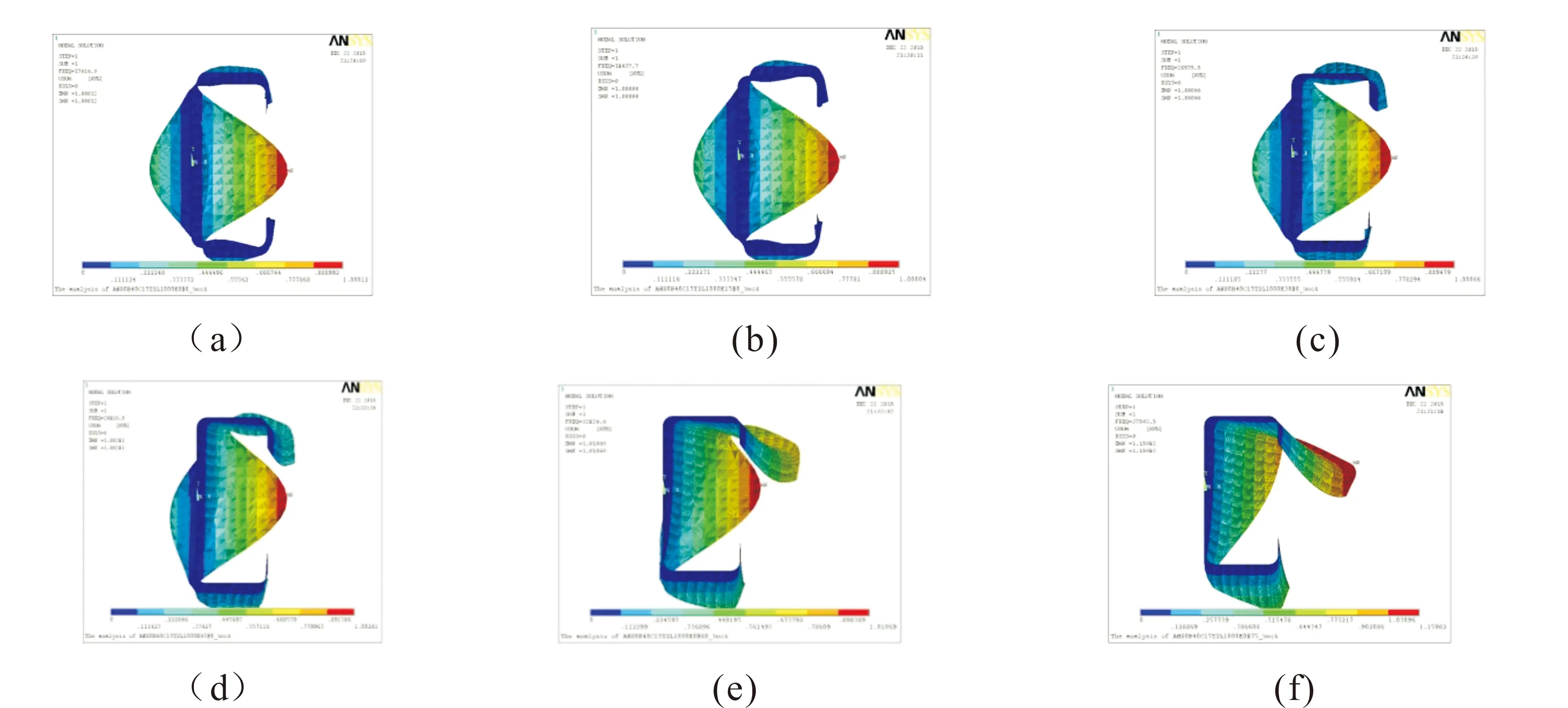
图6　0°到75° C型钢梁的屈曲模态图

图7　侧扭屈曲

结合对钢梁屈曲模态图不同方位的观察，可以清楚地看到，图6(a)中，在0°时，局部屈曲表现得很明显，而且主要发生在腹板上，而到45°时，如图6(d)所示，局部屈曲现象有所减弱，翼缘腹板都有局部屈曲发生，并伴随有较明显的侧扭屈曲，从0°到45°，腹板局部屈曲依次减弱，翼缘局部屈曲部位依次增大。在60°时，从图6 (e)可以明显看到，钢梁腹板的局部屈曲和整体侧扭屈曲，整体侧扭屈曲的出现，使得翼缘处和腹板处的局部屈曲现象得以削弱，到75°时，如图6(f)所示，整体侧扭屈曲更明显，而腹板和翼缘处的局部屈曲很小，到90°时，钢梁只发生整体侧扭屈曲，而没有局部屈曲，如图7所示。

在观察105°到180°之间的六组数据时，发现钢梁上没有出现局部屈曲，出现了不同程度上的整体侧扭屈曲和翼缘和卷边绕腹板翼缘交接处转动形成外翻变形的畸变屈曲，从z轴观察105°到180°的屈曲模态如图8所示。

图8　105°到180°C型钢梁的屈曲模态图

从z轴观察可以清晰的看到跨中原截面和屈曲变形后的截面对比，在105°时，如8(a)所示，钢梁有着明显的整体侧扭屈曲和很小的畸变屈曲，上翼缘有微小程度的外翻，再观察对应120°时的图8(b)、135°时的图8(c)、150°时的图8(d)、165°时的图8(e)、180°时的图8(f)，对比发现，钢梁的扭转转角随着角度的增大而减小，说明整体侧扭屈曲程度随着角度的增大而减小，而上翼缘的外翻角度却和角度成正比，畸变屈曲程度在随着角度变大而变大。

在观察L=1 500 mm，L=2 000 mm的冷弯C型钢梁屈曲模态中发现随着跨长的增加，构件发生整体侧扭屈曲的概率增大了，当L=1 500 mm时，钢梁从0°到60°五组试验中都表现出局部屈曲以及和局部屈曲整体侧扭屈曲的相关屈曲，规律和L=1 000 mm的钢梁一样，局部屈曲程度依次减小，整体侧扭屈曲程度增大，但是钢梁在75°、90°和105°三组试验中都表现为整体侧扭屈曲，从120°到180°的五组试验，也都表现出明显的畸变屈曲和整体侧扭屈曲的相关屈曲，同L=1 000 mm的钢梁的屈曲规律，畸变屈曲程度不断增大，整体侧扭屈曲逐渐减小。当L=2 000 mm时，钢梁的屈曲规律和前两者也大致相同，但是发生整体侧扭屈曲的试验增加到了五组，相比L=1 500 mm时的情况，多了60°和120°两种。综上所述，不难发现，随着跨长的增加，构件发生整体侧扭屈曲的概率增大了，但同时侧扭屈曲荷载却随之减小。

同样选择H80B40C15T2截面的冷弯C型钢梁，有L=1 000 mm，L=1 500 mm和L=2 000 mm三种跨长，分析横向均布荷载与钢梁截面x主轴在0°到180°共13种情况下钢梁的屈曲模态，有限元屈曲分析数据见表2：

表2　H80B40C15T2均布荷载屈曲分析

横向均布荷载下的钢梁屈曲方式和规律与横向集中荷载大致相同，以跨长L=1 000 mm的钢梁为例，同样是从0°到180°，横向均布荷载情况下在0°、15°、30°、45°、60°时出现局部屈曲以及局部屈曲和整体侧扭屈曲的相关屈曲，并且随着角度的增大，局部屈曲程度依次减弱，侧扭屈曲程度依次增强，75°和90°时出现整体侧扭屈曲，在105°到180°，钢梁呈现侧扭屈曲和畸变屈曲的相关屈曲，随着角度的增大，侧扭屈曲程度减小，畸变屈曲程度增强。说明斜向横向均布荷载作用下，构件发生整体侧扭屈曲的概率增大了。在对L=1 500和L=2 000 mm的钢梁的屈曲模态进行观察分析中，得出了与集中荷载相同的结论，随着跨长的增加，构件发生整体侧扭屈曲的概率增加。而且相同跨长的两种不同横向荷载下钢梁屈曲模态的对比也证实了横向均布荷载作用下比起横向集中荷载更易发生整体侧扭屈曲，降低钢梁发生局部屈曲和畸变屈曲的概率。

相比整体侧扭屈曲和畸变屈曲，局部屈曲更能直观的进行屈曲模态的比较，选取集中荷载和均布荷载在0°度时的局部屈曲模态，从截面y轴方向观察，如图9所示。图9(a)是集中荷载的情况，图9(b)是均布荷载的情况。图中的屈曲位移是相对位移，通过表1和表2中0°时局部屈曲荷载的比较，并且观察图9(a)和图9(b)的不同，我们清楚地看到图9(b)中钢梁构件更多区域发生了局部屈曲，证实横向均布荷载，发生局部屈曲的部位更多，屈曲荷载更大，达到横向集中荷载的近两倍。其他角度作用横向荷载发生局部屈曲时，也表现出类似行为。

图9　0°时集中荷载和均布荷载作用下的钢梁屈曲

5　结论

本文通过采集有限元屈曲分析结果进行对比，并集合不同角度斜向横向荷载时钢梁截面的应力分布，得到以下规律。

(1)在横向荷载有一定大小指向x轴正向的分力时，C型钢梁易发生局部屈曲，而有一定大小指向x轴负向的分力时，钢梁易发生畸变屈曲，C型钢梁截面关于x轴对称，当作用有一定大小的y轴上的分力时，钢梁易发生整体侧扭屈曲，当同时有两种情况的分力时，钢梁发生局部屈曲和侧扭屈曲的相关屈曲或者畸变屈曲和侧扭屈曲的相关屈曲。两种横向荷载表现出相同规律，但横向均布荷载作用在构件上的区域更广，受力范围更大，构件整体参与屈曲行为，构件抵御屈曲的能力更强。

(2)当腹板与翼缘交接处上的应力、翼缘和卷边交接处上的应力同为拉应力或压应力时，钢梁易发生整体侧扭屈曲，当腹板与翼缘交接处上应力为压应力而翼缘和卷边交接处上的应力为拉应力时，钢梁易发生局部屈曲，当腹板与翼缘交接处上应力为拉应力而翼缘和卷边交接处上的应力为压应力时，钢梁易发生畸变屈曲。而截面上相对应力大小的变化，会导致局部屈曲和侧扭屈曲的相关屈曲以及畸变屈曲和侧扭屈曲的相关屈曲。

[1]于伟文.冷成型钢结构设计[M].北京：中国水利水电出版社,2003.

[2]何保康，李风，丁国良．冷弯型钢在房屋建筑中的应用与发展[J].焊管，2002，25(5)：8-11.

[3]沈祖炎.《冷弯薄壁型钢结构技术规范》的发展[J].钢结构，2009,24(7):55-58.

[4]陈绍蕃. 钢结构稳定设计指南[M].北京：中国建筑工业出版社, 2013.

[5]Hancock G J.Local,Distortional and Lateral Buckling of I-beams[J].Journal of Structural Division,ASCE,1978,104(11):1787-1798.

[6]Schafer B W,ádány,S.Buckling Analysis of Cold-formed Steel Members using CUFSM:Conventional and Constrained Finite Strip Methods[C].18th International Specialty Conference on Cold-Formed Steel Structures,2006:39-54.

Buckling mode analysis of cold-formed channel beams under biaxial bending

LI Xiang-chao,WAN Hong-xia

(School of Civil Engineering and Architecture,Wuhan University of Technology,Wuhan 430000,China)

Buckling mode affected the cold-formed channel beams in mechanical properties to a certain extent,in order to obtain the relations of buckling mode and biaxial bending,ANSYS finite element software was used to establish SHELl181 shell element finite element model.The instability of the cold-formed channel beams under biaxial bending is analyzed,besides the different buckling modes of steel beams at different angles of oblique transverse force,and the general rules of biaxial bending beam buckling modes are summarized

cold-formed channel beams;biaxial bending;finite element;buckling mode

2016-03-08

李相超(1991—)，男，湖北黄石人，硕士研究生。

1674-7046(2016)04-0019-07

10.14140/j.cnki.hncjxb.2016.04.004

TU392.1

A