基于模糊控制的惯性测量单元温控系统数值分析

李双玉，杨 明，何 青

（北京航天控制仪器研究所，北京100039）

基于模糊控制的惯性测量单元温控系统数值分析

李双玉，杨 明，何 青

（北京航天控制仪器研究所，北京100039）

针对捷联惯性测量单元（IMU）温控系统的高精度、高滞后性和时变性，提出一种基于CFD技术的捷联IMU模糊PID控制器设计方法。首先，对某型号IMU的热量传递机理进行分析，建立IMU传热特性三维数值计算模型，借助CFD软件Fluent的UDF功能实现对IMU数学模型温控系统的模糊PID控制。最后，通过改变环境温度获得IMU数学模型在瞬态计算条件下的温度分布规律，并将IMU不同部位的温升值与试验结果进行对比，分析温度分布对惯性仪表的影响。研究结果能为IMU温控系统的改进和优化提供依据。

惯性测量单元；模糊控制；温控系统；传热特性；数值研究

0　引言

由于捷联惯性测量单元（Inertial Measurement Unit，IMU）中陀螺仪、加速度计等惯性仪表的精度除了受制造工艺、内部结构等本身因素影响以外，还与其所处的环境条件和工作条件密切相关，温度的变化将直接影响仪表的精度，进而影响导航系统的精度。所以，惯性导航系统的温控系统设计效果对保证惯导系统精度和缩短准备时间有重要作用。捷联IMU温控系统具有大滞后性、时变性和高精度等特点，而且在比较大的环境温度变化范围内工作。由于IMU工作环境复杂，采用计算流体力学（Computational Fluid Dynamics，CFD）技术进行温控系统设计，不仅可以获得IMU的全场物理信息和任意监测点的时域变化规律，而且计算模型可以实现批量化处理。如果将传统设计方法与CFD数值仿真技术相结合将大幅提高设计效率，缩短设计周期，降低成本。

基于CFD技术的控制系统研究最早见于20世纪90年代中期美国NASA的刘易斯研究中心［1］，国内在该领域的研究相对较少，西安交通大学的学者对空间场的温控系统建模与控制等进行了研究。传统PID控制的参数整定比较复杂，且适应性较差，而采用模糊PID控制的温控系统可以适应温度非线性时变，适应性较好，可弥补传统PID控制器的缺陷。

本文通过Fluent软件及其UDF功能实现了捷联IMU的三维数值模型在非稳态（瞬态）条件下的模糊PID控制，获得了捷联IMU温度分布及主要测温点的温度变化规律。

1　研究模型及实现方法

1.1计算模型

在捷联惯性测量单元中，对温度敏感的惯性仪表直接安装在IMU本体上，IMU组件有外罩、本体、电子箱和底盖等，惯性仪表包括加速度计和陀螺仪。实际工作中，捷联IMU主要存在三种热量交换方式，分别是固体部件的热传导，固体与空气间的热对流以及热辐射。

在流动和传热的数值计算中，对于三维不可压连续流体，主要涉及如下数学模型。

连续方程：

动量方程：

能量方程：

式中，Su、Sv和Sw为动量方程广义源项，μ为动力黏度，Cp为比热容，k为流体传热系数。由式（1）～式（3）可见，数值求解的方程主要是非线性的偏微分方程，CFD技术通常采用有限体积法、有限元法等对上述非线性方程进行离散并求解。

1.2实现方法

IMU温控系统模糊控制的实现过程主要涉及模糊PID控制器设计、数学模型非稳态计算、测温点数据采集和处理、单值性条件（初始条件和边界条件）设定等。在实际应用中，由于惯性测量单元的不同部位需要不同的温度条件，所以一般需要使用多路温控系统对IMU温度进行调节。

本文模糊PID控制过程如图1所示。首先建立捷联IMU数值计算模型，并在瞬态计算之初设定边界条件，数值计算的时间步即数字温控系统中的采样时间，此外还要设置每个时间步的迭代次数（一般至少20次）。

图1　温控系统模糊控制数值计算原理图Fig.1 Fuzzy control of the temperature control system with methods of CFD

在单个时间步迭代结束时，通过UDF中的宏函数获取测温点的温度数值，本文通过计算测温区域加权平均值来代替测温传感器附近的温度值。

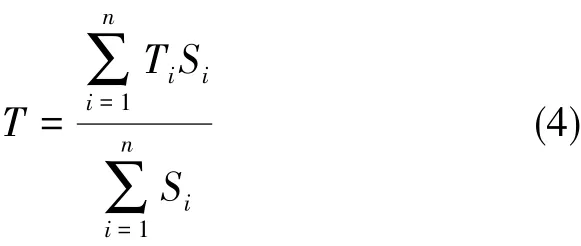
式中，Si代表测温区域第i个单元面面积，Ti为第i个单元的温度。建立IMU三维CAD模型并划分网格，将网格文件导入Fluent中，设定初始边界条件，在UDF中写入模糊PID控制程序，进行初始化操作，求解器开始运行，在时间步迭代末尾通过DEFINE_EXECUT-E_AT_END（）宏函数对测温点的温度进行采集，获得两个采样周期之间的温度误差和误差率，当测温点温度达到目标控制温度3K范围内，程序依据相应的模糊控制规则进行模糊决策，经过模糊控制的参数整定过程获得了PID控制器的相应系数。最后，PID控制器对目标控制变量进行调节并计算得到相应热流密度，最后在每个时间步迭代开始时修改热流密度边界，完成IMU温控系统的模糊PID控制。

2　模糊PID控制器设计

本文针对IMU温控系统滞后性、多路温控等特点，在PID控制器的基础上，通过获得数值迭代过程中的温度误差e和误差变化率ec，根据一定的规则对PID控制的参数进行整定。PID参数模糊自整定主要是找到比例系数Kp、积分作用系数Ki和微分作用系数Kd与e和ec之间的关系。在CFD程序运行过程中，每个时间步迭代结束时，通过检测e和ec并根据模糊控制原理对三个参数进行实时修改，以满足不同e和ec对PID参数的需求。模糊PID控制系统框图如图2所示。

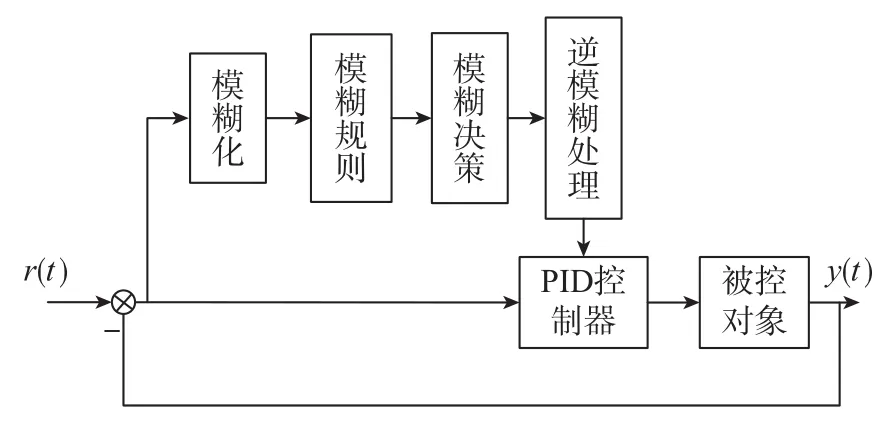
图2　模糊PID控制系统框图Fig.2 Fuzzy control combined with PID

计算机控制是一种采样控制，需要采用离散化的控制算法。本文选用增量式PID控制，该算法不需要对前面的状态误差进行累加，只输出控制量的增量Δu（k）。

式中，k表示第k个采样时刻（k等于时间步数值），u（k）表示第k个采样时刻控制器输出值，e（k）表示与设定温度的偏差值，Δu（k）表示控制量增量。

在实际运行过程中，温控系统必须是实时受控的，而且为了避免积分过饱和现象，温控系统电流的最大值和最小值是已知的，所以温控系统输出量范围如式（6）所示。

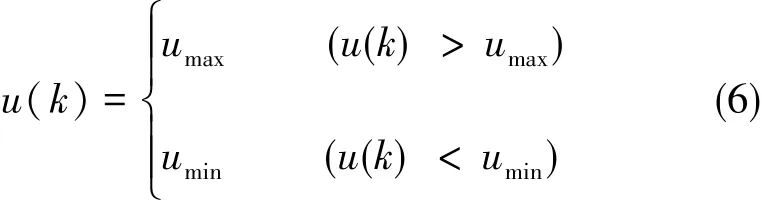
2.1变量模糊化

模糊控制器的输入变量误差和误差变化范围称作变量的基本论域，模糊PID控制器输出为两个参数e和ec，输出为Kp、Ki和Kd的三个参数调整量ΔKp、ΔKi和ΔKd。测温区域1的控制温度为温度328K，测温区域2和测温区域3的控制温度为325K，要求在±3K范围内进行PID控制。离散化后的误差e和误差变化率ec的基本论域为 ｛-3，-3，-1，0，1，2，3｝。e和ec对应模糊语言变量E和Ec，这两个变量所取语言值分别为 ｛负大，负中，负小，零，正小，正中，正大｝，记为｛NB，NM，NS，Z，PS，PM，PB｝，量化论域为｛-3，-2，-1，0，1，2，3｝。

通过隶属度函数来描述IMU温控系统的模糊性，本文选择三角形隶属度函数，解析式和曲线表示如图3所示。可以建立模糊函数E和EC的隶属度函数，并确定E和EC的隶属度函数曲线。

图3　三角形隶属度函数解析式和曲线Fig.3 Membership analytic function and curves

2.2模糊控制规则

PID控制中，比例环节Kp主要是提高系统响应速度，积分环节Ki用来消除稳态误差，微分环节Kd主要用来改善系统的动态特性。模糊PID控制的控制规则主要是根据已有的PID参数整定规律通过模糊控制程序对三个参数进行自动修改。

一般地，控制系统偏差e和变化率 ec越小，系统的不确定性越小。当偏差e绝对值较大时，为了加快系统响应速度，要选取较大的比例系数和微分系数，可设积分系数为零。当偏差和变化率绝对值中等大小时，应设定适当的积分系数和微分系数，为了减小超调量，比例系数要取得小一些。当偏差绝对值较小时，可以选取较大的 Kp、Ki以提高系统稳定性。根据上述规则，编制了表1所示的ΔKp模糊调整规则表。

表1　ΔKp模糊调整规则表Table 1 ΔKpfuzzy tuning rules

同理，也可以写出ΔKi和ΔKd的模糊规则调整规则表，此处不再赘述。通过模糊自整定PID算法得到Kp、Ki和Kd的数值，将其代入增量式PID控制算法计算式，得到对应温度控制量，将其换算成热流密度边界，在每个时间步的开始时对边界条件重新赋值以达到控制IMU数值计算过程的目的。

3　计算结果及分析

3.1IMU及其本体云图及分析

本文主要基于CFD软件ANSYS-Fluent及其UDF（用户自定义函数）功能实现了某型号IMU温度控制系统的模糊PID控制，获得了不同环境温度下IMU测温区域（测温点）的温度随时间变化规律，得到了IMU及其本体（此处指安装惯性仪表的主体部件）的温度分布云图。如图4和图5所示，IMU附近环境温度为313K时捷联IMU及其本体的温度分布云图。

图4　捷联IMU温度分布云图Fig.4 Temperature distribution of the IMU

图5　捷联IMU本体温度分布Fig.5 Temperature distribution of main part

通过分析IMU及其本体的温度分布云图可知，IMU外部温度由于自然对流作用而温度较低；本体上，加速度计、陀螺仪安装位置处的温度比较高；本体与工装接触附近温度较低，在设计时应尽量避免惯性仪表靠近该区域。本体温控系统的加温片粘贴（区域）方案保证了惯性仪表附近的温度差异较小。

3.2环境温度变化对陀螺影响

模糊PID控制器在目标温度±3K范围内开始对控制量 （本文为电流）进行调节，在达到目标温度控制范围之前控制系统以恒定功率对IMU进行加热，由于温控系统是一个纯滞后系统，为了保证工作过程中IMU温度始终处于被控状态，当温度大于目标温度+3K时，温控系统以最低功率对IMU进行加热。图6和图7表示IMU上的陀螺测温点在瞬态计算条件下的温度变化规律。

图6　陀螺测温点1温度变化曲线Fig.6 Variation trends of the first measuring point

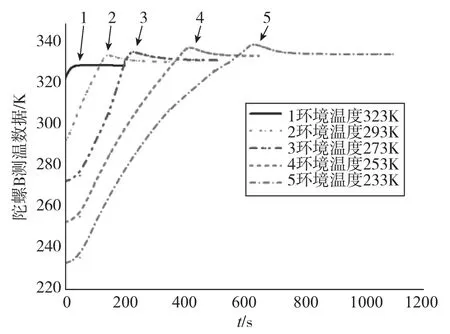
图7　陀螺测温点2温度变化曲线Fig.7 Variation trends of the second measuring point

鉴于惯性仪表不能承受过高的温度变化率（本文标准15K/min），所以在温控系统设计过程中要考虑到惯性仪表附近测温区域的温度变化率。鉴于IMU在达到目标温度±3K范围之前一直采用最大功率加热，所以一般实验或安装条件一致的条件下，温度变化率随环境温度升高而变大。如果环境温度较高时陀螺测温点温度变化率可能超过15K/min，在对温度控制器进行设计过程中需要添加温度变化率判断环节，对温度变化率进行限制，使IMU温度控制全过程符合设计要求。

通过图6、图7可以看出，达到目标控制温度所需时间随环境温度增大而减小，环境温度323K时只需200s即可达到温控要求，而环境温度233K时则需900s以上才能达到温度要求。而且，随着环境温度的降低，陀螺测温点的温度超调量相应增大，但是一般在小于4K，处于合理超调范围之内，具体如表2所示。

表2　陀螺测温点温度Table 2 Temperature of gyroscopes’measuring points

通过表2可以看出，IMU本体设计合理，两个陀螺测温点在不同环境下的温度基本一致。

3.3模糊PID与传统PID计算结果对比

由于陀螺测温点1和2的温度数值和变化规律基本一致，所以可以通过分析相同环境条件下测温点1处模糊PID和传统PID控制的升温曲线来对比二者控制效果。图8所示为陀螺测温点1处模糊PID与传统PID温控效果曲线。

图8　模糊PID与传统PID控制效果对比Fig.8 Comparison with traditional PID control

通过陀螺测温点1处升温曲线可以发现，相同环境下，开始阶段惯组加温装置满功率加热，模糊PID和传统PID温度上升曲线重合。当达到设定的温控范围时，温度控制器开始工作。与传统PID控制方式相比，模糊PID控制器的温度超调量相对较小，且加热到设定温度的工作时间相对较短。通过对比温升曲线可以得出结论，模糊PID控制控制效果优于传统PID控制。

3.4 试验与仿真结果对比

IMU的本体温度变化对惯性仪表的温度影响最大，通过温箱试验获得了IMU本体测温点在263K和313K环境下达到稳定状态时的温度数值。表3所示为试验测得温度数值与温控系统数值仿真获得的数据对比，通过对比发现数值仿真与试验测量结果基本相符，仿真结果满足要求。

表3　试验与仿真结果对比Table 3 Comparison with experimental results

4　结论

本文主要基于CFD技术实现了捷联惯性测量单元温控系统的模糊PID控制，通过Fluent软件的UDF功能对三维数值模型进行了瞬态数值计算，得到了IMU测温点数值随环境温度变化规律，并将主要检测区域的温度数据与试验结果作对比，验证了仿真数据的准确性。根据IMU数值计算结果，结合测温试验数据，可以得到如下结论：

1）建立了捷联IMU温控系统三维数值计算模型，使用Fluent的UDF功能实现了IMU多路温控系统数学模型的模糊PID控制，该方法可以可提高IMU温控系统设计效率，降低了设计成本。

2）获得了IMU及其本体的温度分布云图和主要测温点的数据及温度变化规律。数值计算结果与测温试验数据基本相符，研究结果能为某型号捷联IMU温控系统的设计和改进提供指导。

［1］ 孟庆龙，王元.基于CFD的空间场温度系统建模与控制［J］.浙江大学学报（工学版），2012，46（8）：1479-1484. MENG Qing-long，WANG Yuan.Modelling and control of CFD-based distributed parameter system［J］.Journal of Zhejiang University，2012，46（8）：1479-1484.

［2］ 罗立成.光纤陀螺精密温度控制系统的设计及其研究［D］.哈尔滨工业大学，2011. LUO Li-cheng.Research and designing of high-precision temperature control system for FOG［D］.Harbin Engineering University，2011.

［3］ WANG Jin，LI Yun-ze，WANG Jun.Transient performance and intelligent combination control of a novel spray cooling loop system［J］.Chinese Journal of Aeronautics，2013，26 （5）：1173-1181.

［4］ CAO Jian-peng，Seok-Kwon Jeong，Young-Mi Jung.Fuzzy logiccontrollerdesignwithunevenly-distributed membership function for high performance chamber cooling system［J］.Journal of Central South University，2014，21 （7）：2684-2692.

［5］ LI Ke，LIU Wang-kai，WANG Jun.An intelligent control methodforalargemulti-parameterenvironmental simulation cabin［J］.Chinese Journal of Aeronautics，2013，26（6）：1360-1369.

［6］ 左帅，和婷，尧思远.基于模糊PID控制的半导体激光器温控系统［J］.激光与红外，2014，44（1）：94-97. ZUO Shuai，HE Ting，YAO Si-yuan.Temperature control system for semiconductor laser based on fuzzy PID［J］.Laser&Infrared，2014，44（1）：94-97.

Temperature Field Analysis of Inertial Measurement Unit on Fuzzy Control

LI Shuang-yu，YANG Ming，HE Qing
（Beijing Institute of Aerospace Control Devices，Beijing 100039）

A method based on CFD technology was proposed to improve the performance of the temperature control system in the inertial measurement unit（IMU）with characteristics of high precision，high hysteresis and time-varying.The mechanism of heat transfer in the IMU was analyzed and the software of Fluent with UDF function was utilized to investigate the fuzzy temperature control of the three-dimensional numerical model.The temperature distribution of the IMU was obtained by changing the temperature and boundary with transient calculation.The temperature distribution obtained by numerical calculation was compared with the results of experiment and the influence of temperature distribution on inertial instruments has been investigated.The results of the investigation can guid the design of the temperature control system in the IMU.

inertial measurement unit；fuzzy control；temperature control system；heat transfer；numerical investigation

TK39；TP29

A

1674-5558（2016）01-01117

10.3969/j.issn.1674-5558.2016.04.007

2015-05-05

李双玉，男，硕士，工程师，研究方向为结构设计及流动和传热。