Some Results of Biharmonic Maps

FENG Shu-xiang，PAN Hong

（College of Mathematics and Information Science，Xinyang Normal University，Xinyang 464000，China）



Some Results of Biharmonic Maps

FENG Shu-xiang，PAN Hong

（College of Mathematics and Information Science，Xinyang Normal University，Xinyang 464000，China）

In this paper，we investigate biharmonic maps from a complete Riemannian manifold into a Riemannian manifold with non-positive sectional curvature.We obtain some non-existence results for these maps.

biharmonic maps；harmonic map

2000 MR Subject Classification:58E20，53C21

Article ID:1002—0462（2016）01—0019—08

Chin.Quart.J.of Math.

2016，31（1）：19—26

§1.　Introduction

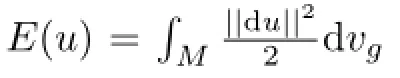
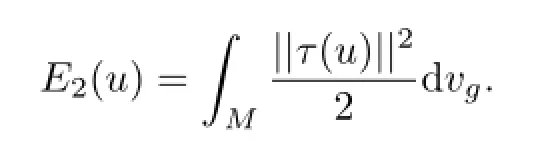
We see that harmonic maps are biharmonic maps and even more，minimizers of the bienergy functional.After G Y Jiang［7］studied the first and second variation formulas of the bienergy E2，there have been extensive studies on biharmonic maps（for instance，see［4，7，10-11，14，16-18］.

For harmonic maps，it is well known that：If a domain manifold（M，g）is complete and has non-negative Ricci curvature and the sectional curvature of a target manifold（N，h）is non-positive，then every energy finite harmonic map is a constant map（cf［15］）.

For biharmonic maps，it is known that：If a non-compact Riemannian manifold（M，g）is complete and has non-negative Ricci curvature and（N，h）has non-positive sectional curvature，then every bienergy finite biharmonic map of（M，g）into（N，h）is harmonic（cf［2］）.

Recently，N Nakauchi，H Urakawa and S Gudmundsson［14］proved that biharmoic map from a complete Riemannian manifold into a non-positive curved manifold with finite bienergy and energy are harmonic.S Maeta［13］proved that biharmoic map from a complete Riemannian manifold into a non-positive curved manifold with finite p-bienergy∫M|τ（u）|pdvg＜∞（p≥2）and energy is harmonic.Y Luo［12］proved that biharmoic map from a complete Riemannian manifold into a non-positive curved manifold which has at least one hyperbolic point with finite p-bienergy∫M|τ（u）|pdvg＜∞（p≥2）is harmonic.

Definition 1.1Let（N，h）be a Riemannian manifold.We say a point x0∈N is a hyperbolic point，if the sectional curvature of any tangent plane at x0is negative.

In this paper，we will show that

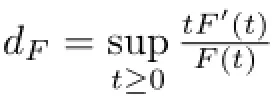
（a）Every biharmonic map u：（M，g）→（N，h）with finite energy and∫MF（|τ（u）|2）dvg＜∞is harmonic.

（b）In the case Vol（M，g）=∞，every biharmonic map u：（M，g）→（N，h）with∫MF（|τ（u）|2）dvg＜∞is harmonic.

（c）In the case N has at least one hyperbolic point and rank（du）≠1，every biharmonic map u：（M，g）→（N，h）with∫MF（|τ（u）|2）dvg＜∞is harmonic.

§2.　Preliminaries

In this section we give more details for the definitions of harmonic maps，biharmonic maps and biharmonic submanifolds.

Let u：（M，g）→（N，h）be a map from an m-dimensional Riemannian manifold（M，g）to an n-dimensional Riemannian manifold（N，h）.The energy of u is defined by

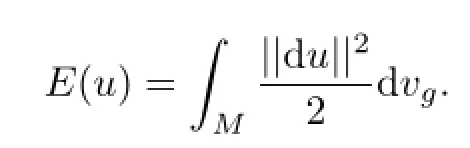
The Euler-Lagrange equation of E is

where we denote by▽the Levi-Civita connection on（M，g）andthe induced Levi-civita connection onis an orthonormal frame field on（M，g）.τ（u）is called the tension field of u.A map u：（M，g）→（N，h）is called a harmonic map if τ（u）=0.

To generalize the notion of harmonic maps，in 1983 J Eells and L Lemaire［5］proposed considering the bienergy functional

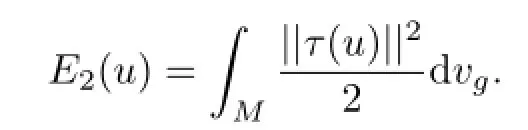
In 1986，G Y Jiang［7］studied the first and second variation formulas of the bienergy E2.The Euler-Lagrange equation of E2is

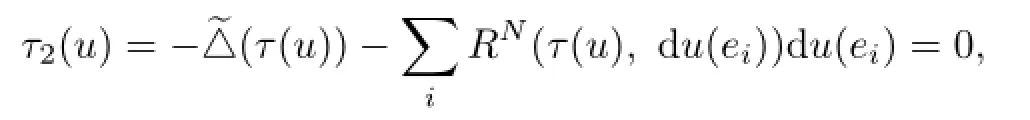
We also recall biharmonic submanifolds.

Let u：（M，g）→（N，h=〈·，·〉）be an isometric immersion from an m-dimensional Riemannian manifold into an n-dimensional Riemannian manifold.We identify du（X）with X∈Γ（TM）for each x∈M.We also denote by〈·，·〉denote the induced metric u-1h.The Gauss formula is given by

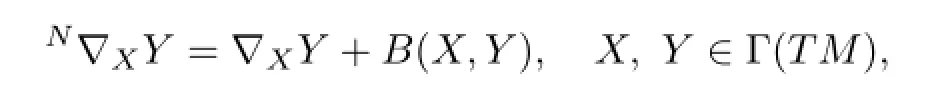
where B is the second fundamental form of M in N.The Weingarten formula is give by

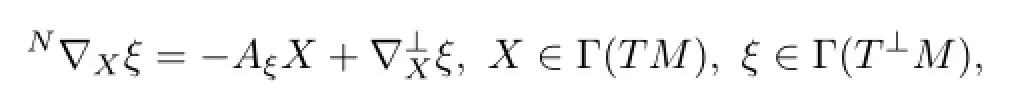
where Aξis the shape operator for a unit normal vector field ξ on M and▽⊥denotes the normal connection on the normal bundle of M in N.For any x∈M，the mean curvature vector field H of M at x is given by

If an isometric u：（M，g）→（N，h）is biharmonic，then M is called a biharmonic submanifold in N.In this case，we remark that the tension field τ（u）of u is written τ（u）=mH，where H is the mean curvature vector field of M.The necessary and sufficient condition for M in N to be biharmonic is the following：

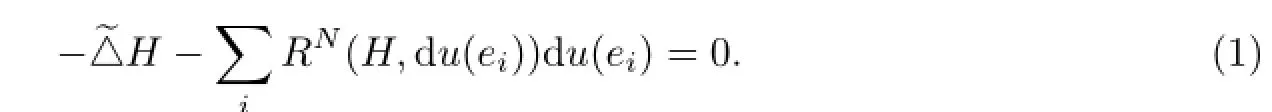
We also need the following Lemma.

Lemma 2.1（Gaffney）［6］Let（M，g）be a complete Riemannian manifold.If a C1a-form α satisfies that∫M|α|dvg＜∞and∫M（δα）dvg＜∞or equivalently，a C1vector X defined by α（Y）=〈X，Y〉（∀Y∈Γ（TM））satisfies that∫M|X|dvg＜∞and∫Mdiv（X）dvg＜∞，then

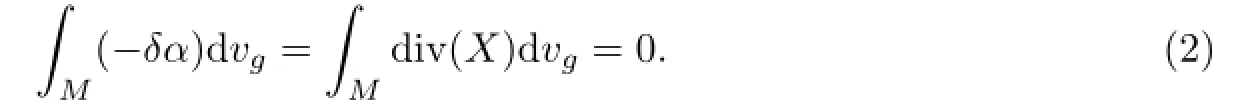
§3.Proof of Theorem 1.2

In this section we will give a proof of Theorem 1.2

Proof Take a fixed point x0∈M and for every r＞0，let us consider the following cut off function λ（x）on M

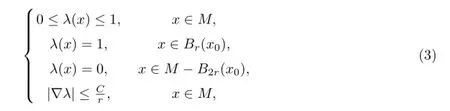
where Br（x0）=｛x∈M：d（x，x0）＜r｝，C is a positive constant and d is the distance of（M，g）. From（1），we have

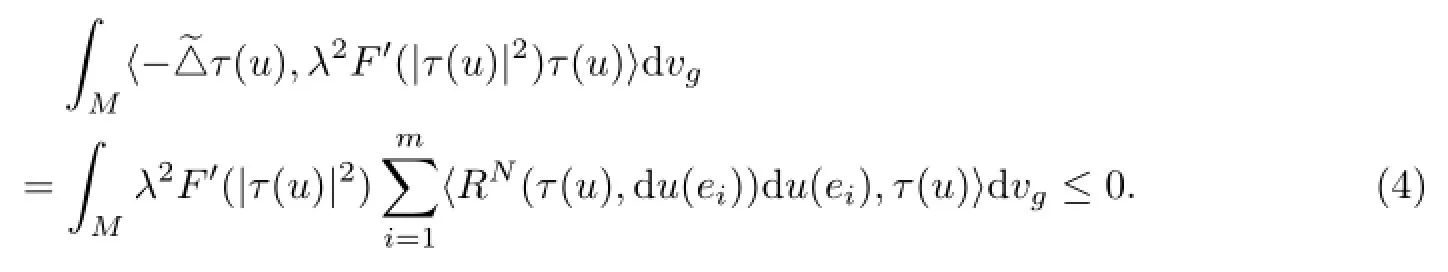
Since the sectional curvature of（N，h）is non-positive.From（4），we have

where the inequality follows fromFrom（5），we have

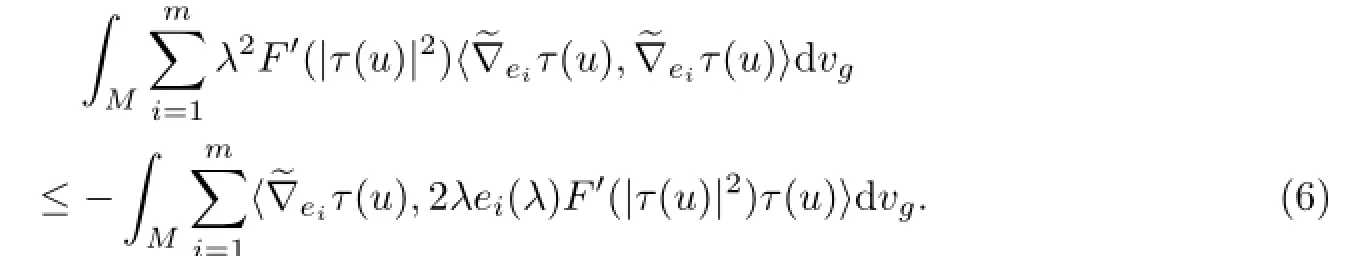
By using the Cauchy-Schwarz inequality，we have

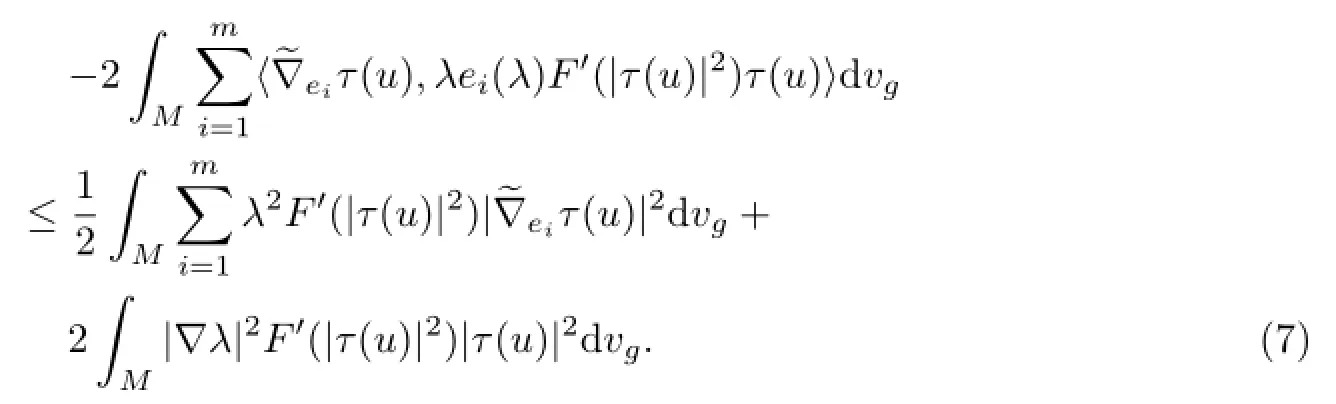
From（6）and（7），we have

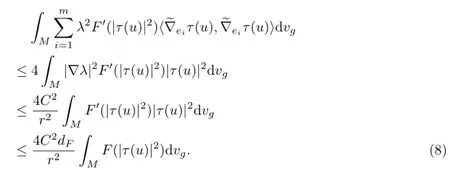
By assumption∫MF（|τ（u）|2）dvg＜∞，the right hand side of（8）goes to zero and left hand side of（8）goes to

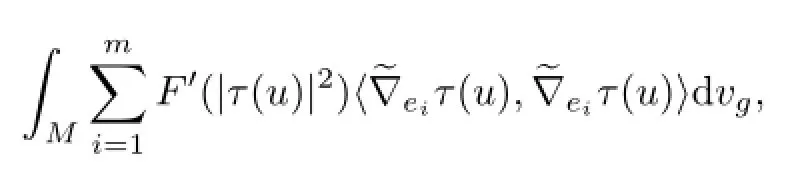
if r→∞，since λ=1 on Br（x0）.Thus we have

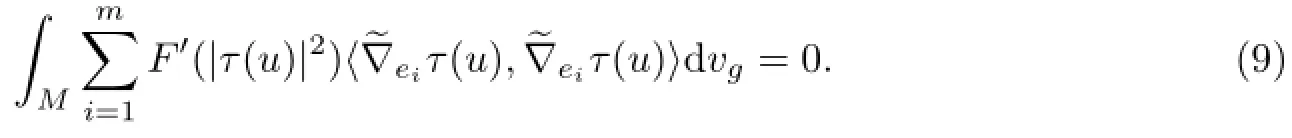
Therefore，we obtain that|τ（u）|is constant andfor any vector field X on M.

Therefore，if Vol（M）=∞and|τ（u）≠0|，then

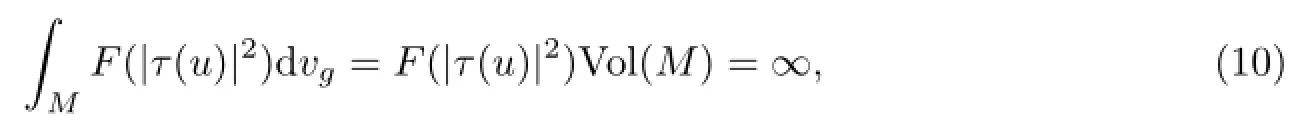
which yields a contradiction.Thus，we have|τ（u）|=0，i.e.，u is harmonic.We have（b）.

For（a），assume both∫MF（|τ（u）|2）dvg＜∞and∫M|du|2dvg＜∞.Define a 1-from α on M defined by

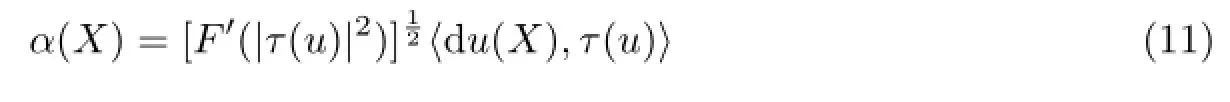
for any vector X∈Γ（TM）.

Note here that

Now we compute

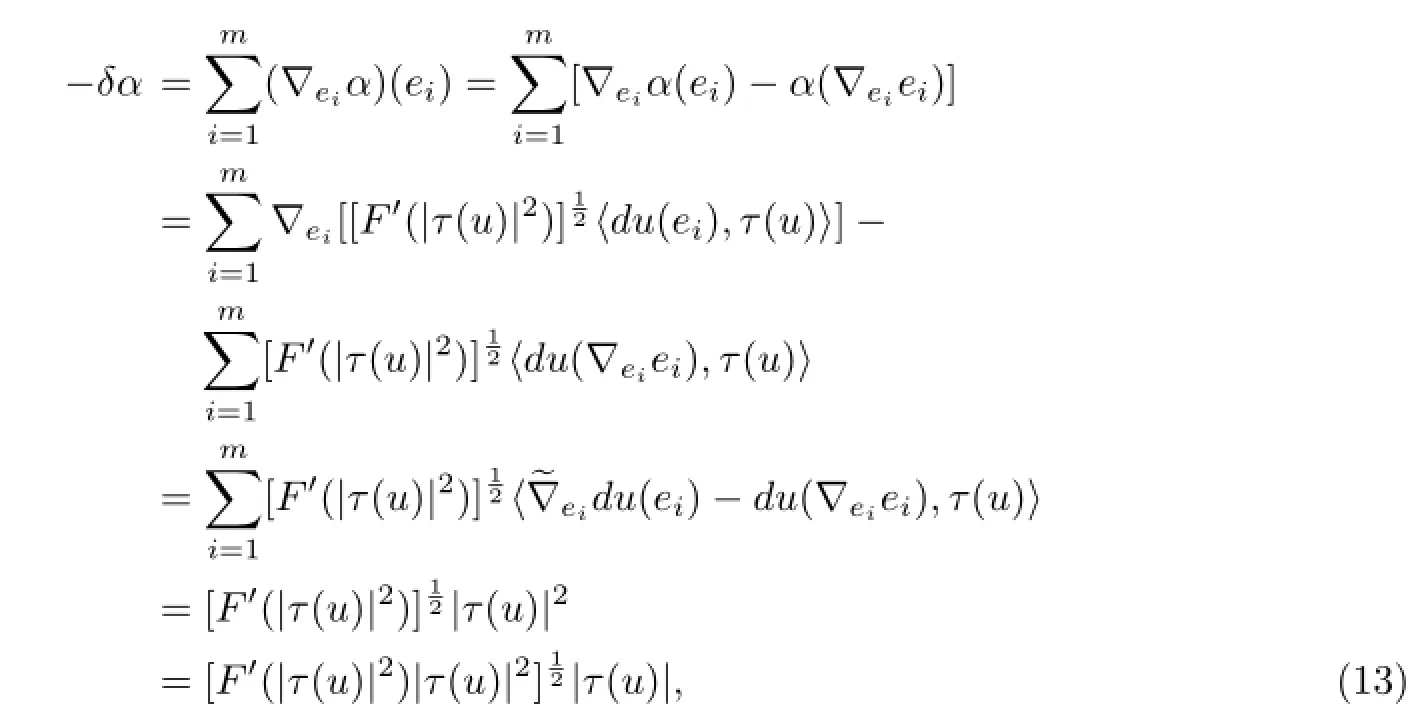
where the fourth equality follows from that|τ（u）|is constant andFrom（13），we have

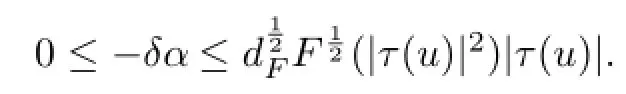
Since∫MF（|τ（u）|2）dvg＜∞and|τ（u）|is constant，the function-δα is also integrable over M. From this and（12），we can apply Lemma 2.1 for the 1-from α.Therefore we have

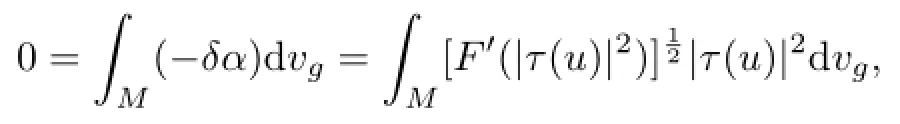
so we have τ（u）=0，that is，u is harmonic.

For（c），since∫MF（|τ（u）|）dvg＜∞，we obtain that|τ（u）|is constant andfor any vector field X on M.We only need to prove that c=0.If not，assume that y0is a hyperbolic point on N；then by smoothness we see that there is a neighborhood around y0∈U⊂N where every point is hyperbolic.Now we discuss two possibilities.

（i）du=0 everywhere in U.Then τ（u）=Trace（▽du）=0 in U，i.e.，c=0.

（ii）There exists a hyperbolic point y1∈U and q∈M，u（q）=y1，such that duqis non-degenerate.We choose geodesic coordinates｛xi，i=1，···，m｝on M around q such that duV（∂x1）≠0（possibly in a smaller neighborhood V of q）.Then by the F-biharmonic equation andfor any vector field X on M，we have in V，

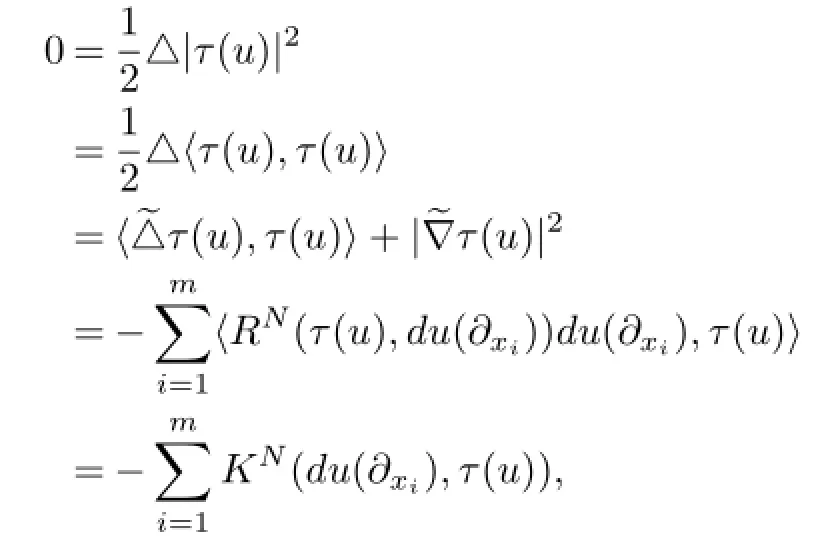
where KN（du（∂xi），τ（u））denotes the sectional curvature at y0of the tangent plane spanned by du（∂xi）and τ（u），i=1，···，m.Since duV（∂x1）≠0 and rank（du）≠1，we have rank（du）|V≥2，there exists a vector field du（∂xj）such that du（∂xj）is not parallel to τ（u），we have

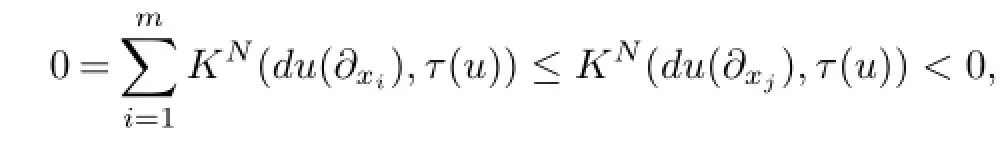
a contradiction.

If a biharmonic map u：（M，g）→（N，h）is an isometric immersion，that is，M is a biharmonic submanifold in N，we obtain the following result.

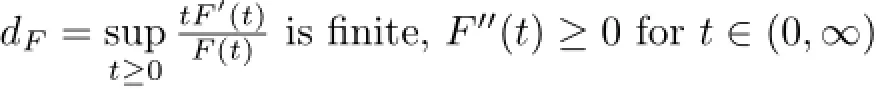
then u is harmonic.

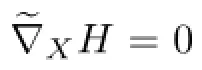
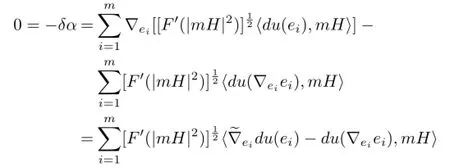
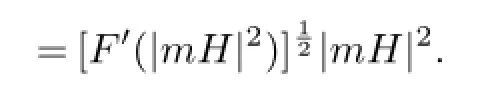
Therefore M is minimal，that is，u is harmonic.

［References］

［1］ARA M.Geometry of F-harmonic maps［J］.Kodai Math J，1999，22：243-263.

［2］BAIRD P，FARDOUN A，OUAKKAS S.Liouville-type theorems for biharmonic maps between Riemannian manifolds［J］.Adv Calc Var，2010，3：49-68.

［3］CADDEO R，MONTALDO S，PIU P.On biharmonic maps［J］.Contemp Math，2001，288：286-290.

［4］CHIANG Yuan-jen.Developments of Harmonic Maps，Wave Maps and Yang-Mills Fields into Biharmonic Maps，Biwave Maps and Bi-Yang-Mills Fields［M］.Basel：Springer Basel，2013.

［5］EELLS J，LEMAIRE L.Selected Topics in Harmonic Maps［M］.Rhode Island Providence：American Mathematical Society，1983.

［6］GAFFNEY M P.A special Stoke’s theorem for complete Riemannian manifold［J］.Ann Math，1954，60：140-145.

［7］JIANG Guo-ying.2-harmonic maps and their first and second variational formulas［J］.Chinese Ann Math，1986，7A：388-402；the English Translation，Note di Matematica，2009，28：209-232.

［8］JIANG Guo-ying.The conservation law for 2-harmonic maps between Riemannian manifolds［J］.Acta Math Sin，1987，30：220-225.

［9］LIU Jian-cheng.Liouville theorems of stable F-harmonic maps for compact convex hypersurfaces［J］.Hiroshima Math J，2006，36：221-234.

［10］LOUBEAU E，ONICIUC C.The index of biharmonic maps in spheres［J］.Compositio Math，2005，141：729-745.

［11］LOUBEAU E，MONTALDO S，ONICIUC C.The stress-energy tensor for biharmonic maps［J］.Math Z，2008，259：503-524.

［12］LUO Yong.Liouville-Type theorems on complete manifolds and non-existence of bi-harmonic maps［J］.J Geom Anal，2014，DOI 10.1007/s12220-014-9521-2.

［13］MAERA S.Biharmonic maps from a complete Riemannian manifold into a non-positively curved manifold［J］. Ann Global Anal Qeom，2014，46：75-85.

［14］NAKAUCHI N，URAKAWA H，GUDMUNDSSON S.Biharmonic maps into a Riemannian manifold of non-positive curvature［J］.Results Math，2013，63：467-474.

［15］SCHOEN R，YAU S T.Harmonic maps and the topology of stable hypersurfaces and manifolds with nonnegative Ricci curvature［J］.Comment Math Helv，1976，51：333-341.

［16］ONICIUC C.Biharmonic maps between Riemannian manifolds［J］.Analele Stintifice Ale Univer Allcuza Iasi，2002，2：237-248.

［17］WANG Chang-you.Remarks on biharmonic maps into spheres［J］.Calc Var Partial Differential Equations，2004，21：221-242.

［18］WANG Chang-you.Biharmonic maps from R4into Riemannian manifold［J］.Math Z，2004，247：65-87.

O186.15Document code:A

date：2014-09-19

Supported by the Natural Natural Science Foundation of China（11201400）；Supported by the Basic and Frontier Technology Research Project of Henan Province（142300410433）；Supported by the Project for Youth Teacher of Xinyang Normal University（2014-QN-061）

Biographies：FENG Shu-xiang（1978-），female，native of Heze，Shandong，a lecturer of Xinyang Normal University，M.S.D.，engages in differential geometry；PAN Hong（1980-），female，native of Zaozhuang，Shandong，a lecturer of Xinyang Normal University，M.S.D.，engages in differential geometry.