高速列车构架蛇行波实测统计分析
2016-09-21余翠英毛建红
余翠英 向 俊 毛建红,3 龚 凯
(1中南大学土木工程学院, 长沙 410075)(2南昌理工学院建筑工程学院, 南昌 330044)(3华东交通大学土木建筑学院, 南昌330013)
高速列车构架蛇行波实测统计分析
余翠英1,2向俊1毛建红1,3龚凯1
(1中南大学土木工程学院, 长沙 410075)(2南昌理工学院建筑工程学院, 南昌 330044)(3华东交通大学土木建筑学院, 南昌330013)
为完善运营速度290和300 km/h的高速列车-轨道(桥梁)时变系统横向激振源的基础资料,基于实测的高速列车构架蛇行波资料,运用工程概率数值分析方法,对高速列车构架蛇行波标准差σ进行了统计,并运用三角级数模型及Monte-Carlo法随机模拟出高速列车人工构架蛇行波.研究结果表明,随着速度由290 km/h上升到300 km/h,高速列车构架蛇行波标准差σp(p=99%)由0.238 3g上升到0.245 1g,且高速列车人工构架蛇行波峰值分别为0.843g,0.883g,与实测构架蛇行波峰值接近,初步验证了构架蛇行波标准差σp的合理性,从而为高速列车-轨道(桥梁)系统横向振动分析提供了良好的激振源.
高速列车;构架蛇行波;标准差;激振源;统计分析
列车-轨道(桥梁)耦合系统横向振动计算中,国内外学者大都采用轨道横向不平顺作为系统横向振动的激励输入[1-5].实际上引起此系统横向振动的因素很多,如轮轨缺陷与损伤、轨道不平顺等,因此考虑所有随机因素来分析此系统的随机振动[6]是非常困难的.而车辆构架蛇行波不仅反映了引起此系统横向振动各因素的影响,还反映了轮轨实际接触状态,这是以构架蛇行波为横向激振源的特点.研究人员提出了列车-轨道(桥梁)耦合系统振动的能量随机分析理论,确认了车辆构架人工蛇行波标准差为该系统随机分析的输入能量[7-9],证明了构架人工蛇行波为车轨系统横向激振源的合理性[10],并取得了许多研究成果[7-13].
文献[14-17]就空重混编列车和秦沈客运专线高速列车构架蛇行波进行了大量的试验研究.由于受诸多因素影响,鲜有针对我国其他高速铁路构架蛇行波进行的统计分析.为不断完善高速列车-轨道(桥梁)系统横向激振源的基础资料,本文对京沪高速铁路客运专线的构架蛇行波实测资料进行研究,统计分析出速度290和300 km/h的高速列车构架蛇行波标准差,并运用三角级数模型及Monte-Carlo法随机模拟出高速列车人工构架蛇行波,从而为此系统横向振动激振源提供了重要的基础数据.
1 高速列车构架蛇行波数据来源及处理
1.1数据来源
为计算运营速度290和300 km/h的高速列车构架蛇行波标准差,本文对收集到的京沪高速铁路2014年1—6月的高速列车构架动态检测数据进行统计.高速列车运行速度为288.7~303.5 km/h,采样间距0.25 m,检测精度为1.5 mm,测试里程范围为500+000~550+200 km区间段.限于篇幅,本文仅列出部分线路区间实测的高速列车构架蛇行波形图,如图1所示.
1.2实测数据预处理
因检测装置一般安装在高速列车构架上,测试环境的恶劣、传感器的温度漂移及人工标定等不利因素易导致检测系统出现误差.在统计分析车辆的构架蛇行波标准差前需对高速列车构架蛇行波数据进行预处理(见图2(a)),以确保标准差σp计算的准确性和可靠性.本文以不平顺变化率法作为构架蛇行波的数据异常值判断标准,对实测数据进行检查并剔除数据的信息错误;同时对异常值剔除后的样本数据以截止频率0.4~200 Hz进行带通滤波,分别以加速度的0.15%和99.85%作为其最小值和最大值,统计分析得到速度为300 km/h时高速列车构架的横向加速度峰值为0.874g,如图2(b)所示.
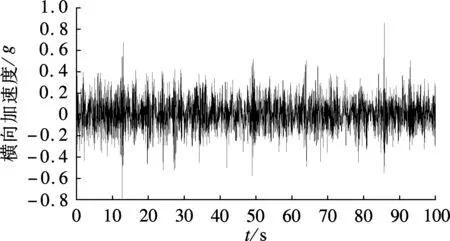
(b) 带通滤波
2 构架蛇行波标准差σ的统计方法
2.1构架蛇行波标准差的概率密度函数拟合方法
依据京沪高速铁路测试的车辆构架蛇行波数据,将8 000个数据(即2 000 m)作为一个样本单元,统计分析各样本单元的标准差,并绘制各样本标准差的频率直方图.统计分析的样本数据包含正线的线路、桥梁及隧道等的区间测试数据,但不含站线测试数据.因实测构架蛇行波的频率直方图分布属于多峰分布,宜采用工程概率数值分析方法,对傅里叶级数f(x)进行拟合,统计出具有要求概率水平的标准差.一般工程计算中,取三角级数前20项可满足精度要求,即N≥20.具体方法如下:
设构架蛇行波标准差的概率密度函数f(x)定义在[0,L]区间上,频率直方图Bn为[xn,xn+1]⊂[0,L]的脉冲函数,m为频率直方图中区间等分数.则
(1)
式中,
(2)
(3)
2.2具有99%概率水平的构架蛇行波标准差统计
显然,高速列车构架蛇行波频率直方图的总面积等于1,且拟合概率密度函数f(x)包络了所有样本标准差的频率直方图, 即f(x)必须满足如下条件:
f(x)≥0x∈[0,L]
(4)
(5)
由此可求出随机变量x(x∈[0,L])在任一区间的概率,其分布函数F(x)如下:
(6)
设X∈[a,b]⊂[0,L]划为m等分,即L/m,要求概率水平p=99%,允许误差ε=0.005~0.010,则
(7)
(8)
(9)
式中,n=1,2,…,m;σp为具有99%概率水平的标准差.
2.3人工构架蛇行波的模拟方法
求出高速列车构架蛇行波标准差σp后,运用三角级数模型及Monte-Carlo方法随机模拟出具有要求概率的构架蛇行波,即人工构架蛇行波.随机模拟函数y(t)为
(10)
φk=2πx(k)
(11)
ωk=ωl+(ωu-ωl)x(k)
(12)
式中,Ak(σp)与ωk,φk是相互独立的;x(k)为[0,1]区间的随机变量,当k=1,2,…,N时是相互独立的;Ak(σp)是均值为零、标准差为σp的高斯随机函数,当k=1,2,…,N时是相互独立的;φk为[0,2π]区间的随机变量,当k=1,2,…,N时是相互独立的;ωk为[ωl,ωu]区间的随机变量,当k=1,2,…,N时也是相互独立的;ωu,ωl分别为构架蛇行波基本圆频率的上限和下限[18].
3 构架蛇行波计算结果及分析
3.1构架蛇行波标准差σ的统计分析
利用第2节的方法对车速290和300km/h的京沪线高速列车构架蛇行波标准差进行统计分析(采用的频率直方图区间等分数m=40),结果如图3所示.可见,统计分析的高速列车构架蛇行波标准差的多峰分布频率直方图与概率密度函数曲线拟合良好,其中速度为290km/h的高速列车构架蛇行波标准差σ分布范围为0.096g~0.289g,求出的具有要求概率水平的高速列车构架蛇行波标准差σp=0.238 3g(p=99%);同理统计出车速为300km/h的构架蛇行波标准差分布范围为0.133g~0.300g,求出的标准差σp=0.245 1g(p=99%).可见,σp随车速v的提高而增大,这说明车速越高,输入高速列车-轨道(桥梁)系统的能量越大.构架蛇行波标准差σ的波动与线路轨道状态相关,轨道平顺性好时σ较小,轨道平顺性差时σ较大.因实测线路轨道不平顺状态具有随机性,σ具有波动性,所以要统计具有99%概率水平的标准差σp.
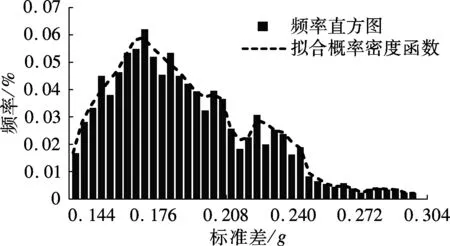
(b) 速度300 km/h(样本量为800 022)
3.2人工构架蛇行波的模拟及初步验证
按照第3.1节求出的高速列车构架蛇行波能量标准差进行随机模拟.限于篇幅,本文仅列出速度为290和300 km/h的构架蛇行波标准差的部分随机模拟结果,并与具有代表性的实测构架蛇行波进行对比.由图4可以看出,速度为290 km/h的高速列车构架蛇行波标准差为0.238 3g,随机模拟的人工构架蛇行波峰值为0.843g,与实测构架蛇行波峰值0.828g接近;速度为300 km/h的高速列车构架蛇行波标准差为0.245 1g,随机模拟的人工构架蛇行波峰值为0.883g,与实测得到的高速列车构架加速度峰值0.874g相近.可见,随机模拟结果与实测峰值基本吻合,初步证明人工构架蛇行波标准差的合理性.此外还可以看出,构架蛇行波标准差σp越大,则随机模拟的人工构架蛇行波峰值也越大.从能量的角度分析可知,构架蛇行波标准差确实反映了此系统的输入能量,标准差越大,输入此系统能量越大,此系统随机振动响应也就越大.

(a) 速度290 km/h

(b) 速度300 km/h
4 结语
基于京沪高速列车构架蛇行波的实测数据,统计分析出了运营速度为290和300 km/h时具有99%概率水平的构架蛇行波标准差分别为0.238 3g和0.245 1g,且随机模拟的人工构架蛇行波峰值与对应速度的构架蛇行波实测值接近,初步验证了列车构架蛇行波标准差的合理性.本文统计分析的构架蛇行波标准差确实反映了此系统的输入能量,进一步完善了运营速度为290和300 km/h的高速列车-轨道(桥梁)耦合系统横向激振源的基础资料.300 km/h以上的构架蛇行波标准差资料还需继续收集.
构架蛇行波标准差反映了轨道不平顺状态,期望构架蛇行波列入轨检车常规检测项目,以便于收集大量的实测资料进行统计分析,建成我国高速列车构架蛇行波数据库,为我国轨道几何不平顺的维修养护提供一定的指导.
References)
[1]翟婉明.车辆-轨道耦合动力学 [M]. 3版. 北京: 科学出版社,2007:88-114.
[2]Xia H, Guo W W, Zhang N, et al. Dynamic analysis of a train-bridge system under wind action[J].Computers&Structures, 2008, 86(19/20):1845-1855. DOI:10.1016/j.compstruc.2008.04.007.
[3]Jin X S, Xiao X B, Ling L, et al. Study on safety boundary for high-speed train running in severe environments[J].InternationalJournalofRailTransportation, 2013, 1(1/2):87-108. DOI:10.1080/23248378.2013.790138.
[4]Eom B G, Lee H S. Assessment of running safety of railway vehicles using multibody dynamics[J].InternationalJournalofPrecisionEngineeringandManufacturing, 2010, 11(2):315-320. DOI:10.1007/s12541-010-0036-x.
[5]Popp K, Kruse H, Kaiser I. Vehicle-track dynamics in the mid-frequency range[J].VehicleSystemDynamics, 1999, 31(5):423-464. DOI:10.1076/vesd.31.5.423.8363.
[6]星谷胜.随机振动分析[M].常宝奇,译.北京:地震出版社,1977:42-99.
[7]曾庆元,郭向荣.列车-桥梁时变系统振动分析理论与应用[M]. 北京:中国铁道出版社,1999:94-111.
[8]李德建, 曾庆元, 王荣辉, 等. 列车-轨道时变系统横向振动能量随机分析方法[J]. 振动工程学报,2000, 13(2):307-313. DOI:10.3969/j.issn.1004-4523.2000.02.023.
Li Dejian, Zeng Qingyuan, Wang Ronghui, et al. Stochastic analysis method of lateral vibration energy for train-track time-varying system[J].JournalofVibrationEngineering, 2000, 13(2):307-313. DOI:10.3969/j.issn.1004-4523.2000.02.023.(in Chinese)
[9]曾庆元,向俊,周智辉,等.列车脱轨分析理论与应用[M].长沙:中南大学出版社,2006: 125-144.
[10]向俊, 曾庆元. 再论构架蛇行波作为车轨(桥)时变系统横向振动激振源的合理性[J]. 长沙铁道学院学报, 2003, 21(1):1-7. DOI:10.3969/j.issn.1672-7029.2003.01.001.
Xiang Jun, Zeng Qingyuan. Further discussion on the rationality of bogie frame crawl waves as lateral vibration source of train-track(bridge) time-variant system[J].JournalofChangshaRailwayUniversity, 2003, 21(1):1-7. DOI:10.3969/j.issn.1672-7029.2003.01.001.(in Chinese)
[11]Xiang J, Zeng Q Y. Mechanism and energy random analysis of train derailment on railway bridges[J].InternationalJournalofStructuralStabilityandDynamics, 2009, 9(4):585-605. DOI:10.1142/s0219455409003193.
[12]Xiang J, He D, Zeng Q Y. Effect of cross-wind on spatial vibration responses of train and track system[J].JournalofCentralSouthUniversityofTechnology, 2009, 16(3):520-524. DOI:10.1007/s11771-009-0086-3.
[13]龚凯, 向俊, 余翠英, 等. 曲线上货物列车超速引起的脱轨过程分析[J]. 东南大学学报(自然科学版),2015, 45(1):172-177. DOI:10.3969/j.issn.1001-0505.2015.01.030.
Gong Kai, Xiang Jun, Yu Cuiying, et al. Analysis on freight train derailment course induced by overspeed in curve[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015, 45(1):172-177. DOI:10.3969/j.issn.1001-0505.2015.01.030.(in Chinese)
[14]王荣辉,郭向荣,曾庆元. 高速列车构架人工蛇行波的随机模拟方法[J]. 长沙铁道学院学报,1995,13(2):1-7.
Wang Ronghui,Guo Xiangrong,Zeng Qingyuan. Random simulating method of artificial crawl wave of high speed train frame [J].JournalofChangshaRailwayUniversity,1995,13(2):1-7.(in Chinese)
[15]向俊, 曾庆元, 娄平, 等. 空重混编列车构架蛇行波标准差试验研究[J]. 实验力学, 2002, 17(3):376-384. DOI:10.3969/j.issn.1001-4888.2002.03.021.
Xiang Jun, Zeng Qingyuan, Lou Ping, et al. A research on the mean square deviation of transverse vibration wave of truck side frame for empty and loaded wagon mixing composition train[J].JournalofExperimentalMechanics, 2002, 17(3):376-384.DOI:10.3969/j.issn.1001-4888.2002.03.021.(in Chinese)
[16]向俊, 周智辉, 娄平, 等. 秦沈客运专线高速列车构架蛇行波标准差的试验研究[J]. 实验力学, 2004,19(4):415-422. DOI:10.3969/j.issn.1001-4888.2004.04.004.
Xiang Jun, Zhou Zhihui, Lou Ping, et al. A test research on mean square deviation of hunting wave of bogie frame of high-speed train running on the Qing-Shen passenger railway line[J].JournalofExperimentalMechanics, 2004, 19(4):415-422. DOI:10.3969/j.issn.1001-4888.2004.04.004.(in Chinese)
[17]王媛, 向俊. 秦沈客运专线高速列车构架人工蛇行波的随机模拟[J]. 铁道科学与工程学报, 2005,2(1):45-50. DOI:10.3969/j.issn.1672-7029.2005.01.010.
Wang Yuan, Xiang Jun. Random simulation of artificial hunting wave of bogie frame of high-speed train running on the Qin-Shen passenger railway line[J].JournalofRailwayScienceandEngineering, 2005, 2(1):45-50. DOI:10.3969/j.issn.1672-7029.2005.01.010.(in Chinese)
[18]王福天.车辆动力学[M]. 北京:中国铁道出版社,1989: 91-93.
Statistical analysis on field-test hunting wave of bogie frame for high-speed train
Yu Cuiying1,2Xiang Jun1Mao Jianhong1,3Gong Kai1
(1School of Civil Engineering, Central South University, Changsha 410075, China) (2School of Architectural Engineering, Nanchang Institute of Technology, Nanchang 330044, China) (3School of Civil and Architectural Engineering, East China Jiaotong University, Nanchang 330013, China)
To perfectng the fundamental data of the lateral exciting source of the high-speed train and track (bridge) time-variant system at the speeds of 290 and 300 km/h, the standard deviationσof the bogie frame hunting wave was studied based on the actual measured bogie frame hunting wave of high-speed train by the method of engineering probability numerical analysis. Meanwhile, the artificial hunting wave of the bogie frame for high-speed train was randomly simulated by the trigonometric series model and the Monte-Carlo method. The results show that, when the speed increases from 290 km/h to 300 km/h, the standard deviationσp(p=99%) of the bogie frame hunting wave is increased from 0.238 3gto 0.245 1g. The maximum values of the artificial hunting wave of the bogie frame for high-speed train are 0.843gand 0.883g, respectively, which agree with those of the field-test hunting wave of the bogie frame. The standard deviationσpof the bogie frame hunting wave is verified to be reasonable, and it can be provided as a good exciting source for lateral vibration analysis of the high-speed vehicle and track (bridge) system.
high-speed train; hunting wave of bogie frame; standard deviation; exciting source; statistical analysis
10.3969/j.issn.1001-0505.2016.04.034
2015-12-14.作者简介: 余翠英(1976—),女,博士生,高级工程师;向俊(联系人),男,博士,教授,博士生导师,jxiang@csu.edu.cn.
国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113)、高等学校博士学科点专项科研基金资助项目(20100162110022) 、江西省青年科学基金资助项目(20142BAB216003)、江西省教育厅科技资助项目(GJJ151173,GJJ151175) 、西南交通大学牵引动力国家重点实验室开放课题资助项目(TPL0901,TPL1214).
10.3969/j.issn.1001-0505.2016.04.034.
U213.2
A
1001-0505(2016)04-0879-05
引用本文: 余翠英,向俊,毛建红,等.高速列车构架蛇行波实测统计分析[J].东南大学学报(自然科学版),2016,46(4):879-883.
