基于BP神经网络和粒子群算法的钢管混凝土拱桥可靠度分析

崔凤坤,　王虎军,　徐　岳,　董峰辉

(1.长安大学 公路学院，陕西 西安　710064; 2.同济大学 土木工程学院，上海　200092)



基于BP神经网络和粒子群算法的钢管混凝土拱桥可靠度分析

崔凤坤1,王虎军1,徐岳1,董峰辉2

(1.长安大学 公路学院，陕西 西安710064; 2.同济大学 土木工程学院，上海200092)

文章针对大跨径钢管混凝土拱桥结构可靠度求解困难的问题,将BP神经网络与粒子群算法引入拱桥可靠度分析领域,首先利用BP神经网络对结构极限状态函数进行拟合,将高度非线性的极限状态方程显式化,然后采用粒子群算法全局搜索验算点并求解可靠指标。计算分析结果表明,BP神经网络和粒子群算法弥补了传统可靠度分析方法的不足,提高了计算精度,为大跨径桥梁结构可靠度研究提供了新的思路和手段。

钢管混凝土拱桥;神经网络;粒子群算法;可靠度;可靠指标

0　引　　言

钢管混凝土拱桥具有自重轻、承载能力强及抗震性能好等突出优点,因其较好地解决了拱桥设计与施工的难题,是迄今为止大跨径桥梁中比较有竞争力的桥型之一。随着钢管混凝土拱桥设计理念和施工技术的不断创新,桥梁跨径越来越大,结构越来越柔,对其进行精确的可靠度分析显得尤为重要。

考虑到钢管混凝土结构的复杂性及大跨径桥梁双重非线性的影响,结构在某一特定失效模式下的极限状态函数一般为高度的非线性方程,很难得到准确的显式表达式,因此无法直接利用传统的一次二阶矩法求解可靠指标。虽然蒙特卡罗法、随机有限元法及响应面法可解决这个问题,但都存在各自的不足。其中,蒙特卡罗法需要进行大量的反复抽样,对于结构可靠度分析而言,则需要进行反复的有限元计算,不适用于大跨径钢管混凝土拱桥这种复杂结构的可靠度分析。随机有限元法需要专门的有限元软件,编制难度很大,不易在实际工程中进行应用、推广。响应面法采用多项式函数(通常为二次多项式)逼近结构极限状态函数,以此来代替确定性有限元分析[1],文献[2]的研究表明多项式函数无法以任意精度逼近任意非线性映射。

近年来,快速发展的神经网络为复杂桥梁结构可靠度分析提供了新的思路,神经网络具有高效的非线性映射和泛化预测能力,可以精确地逼近复杂结构随机变量和响应量的映射关系,这恰好弥补了传统响应面法的不足,因此可以通过神经网络解决极限状态函数显式化的问题。钢管混凝土拱桥可靠度分析中的另一个关键问题是可靠指标的求解,当已知显式化的结构极限状态方程后,目前往往通过JC法求解可靠指标。文献[3]指出JC法仅适用于结构功能函数非线性程度不高的情况,否则很难收敛,而大跨径钢管混凝土拱桥极限状态函数一般具有高度的非线性,使用JC法一般无法求得准确的可靠指标。粒子群算法作为一种新兴的群体智能进化算法,在非线性函数极值寻优方面具有突出的优势,因此将粒子群算法推广到复杂结构可靠度求解领域具有重要的实用价值。

1　BP神经网络应用原理

1.1基本概念

BP神经网络[4]是由大量简单的计算元件(即神经元)按一定规则连接而成的自适应非线性结构,模拟了人类神经系统加工、处理和联想记忆信息的过程,因而具有很好的学习、预测及非线性映射能力。

BP神经网络是一种多层前馈神经网络,其最主要的特点是信号前向传递和误差的反向传播。在向前传递过程中,信号经隐含层从输入层到输出层,如果输出的结果不能满足期望,则网络转入反向传播,根据目标值和预测值的误差来调整网络结构的权值和阈值,从而使BP神经网络的预测结果不断逼近期望的结果。

以单层BP神经网络为例进行说明,单层BP神经网络的基本结构如图1所示。

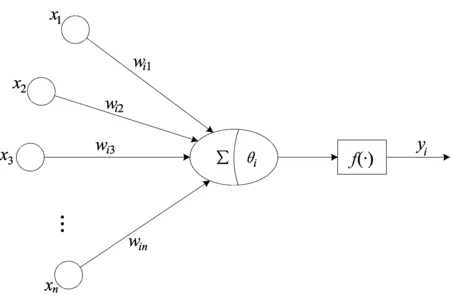
图1　单层BP神经网络模型

单个神经元的数学模型为:

(1)

其中,f(·)为传递函数; xj为神经元的输入值;yi为神经元的输出值; mij、θi分别为BP神经网络的权值和阈值。

传递函数的常用形式有purelin函数、logsig函数、tansig函数3种,即

(2)

(3)

(4)

1.2参数的确定

运用BP神经网络拟合复杂结构极限状态函数,首先需要确定神经网络结构的参数,主要包括神经网络的层数、各层神经元的数目和传递函数的形式等。

文献[5]的研究证明,只要具有足够数量的隐含层神经元数目,一个3层BP神经网络可以以任意精度逼近非线性函数,综合考虑计算的便捷性和结果的准确性,一般采用3层BP神经网络进行结构可靠度分析。

输入层神经元的数目根据结构的设计随机变量(面积、弹性模量等)确定,输出层神经元个数由结构响应量(内力、位移等)确定。而隐含层神经元个数一般通过试算确定,可先确定隐含层神经元数目个数的初值h,然后根据网络的预测误差调整隐层神经元个数。h的计算公式为：

h=lbm

(5)

其中,m为输入层神经元数目。

一般情况下,隐含层的传递函数选logsig函数,输出层的传递函数选purelin函数。

1.3样本点的选择

在结构可靠度分析中,BP神经网络的训练样本需要通过确定性的结构有限元分析获得。对于钢管混凝土拱桥这种复杂的结构形式,进行有限元分析需要耗费大量机时,因此,在满足求解精度的前提下,尽量减少样本规模具有重要的意义。

均匀设计法[6]是由方开泰教授和数学家王元共同提出的一种将数论和多元统计相结合的实验设计方法。通过合理的设计让样本点均匀地分布在试验范围内,达到样本点具有更好的代表性的目的,从而用较少的样本点取得尽可能充分的系统信息。均匀设计表可通过数理统计系统DPS生成,具体使用方法可参考文献[7],限于篇幅本文不再赘述。

由于结构各随机变量的数值相差很大,如果直接将其作为训练样本,神经网络学习时会因过大的权值调整而导致小数信息被大数淹没,进而导致学习失败。因此,应将训练样本归一化或标准化处理后再用于神经网络学习。

2　粒子群算法应用原理

2.1基本概念

粒子群算法[8]将粒子作为基本个体,使用速度、位置和适应度来表示每个粒子的群体特征。在极值寻优问题中,每个粒子的速度、位置根据自身及其他粒子的移动经验不断进行动态调整,从而达到更快向极值逼近的目的。

包含d个自变量的函数的解构成一个D维的搜索空间,在搜索空间中随机分布着n个可以自由运动的粒子,每个粒子在搜索空间的位置(函数的潜在解)用Xi=(xi1,xi2,…,xid)表示,每个粒子相应的速度用Vi=(vi1,vi2,…,vid)表示,每个粒子更新自身位置和速度的进化方程如下:

(6)

(7)

其中,i为粒子的编号;j为粒子的维数;w为惯性权重;t为当前的迭代次数;c1、c2为加速度因子,其值非负;r1、r2为随机因子,其值位于[0,1]; pi,j为i粒子个体最优值对应的位置;pg,j为整个粒子群最优值对应的位置。

为了防止粒子在搜索空间中盲目搜索,应对粒子的位置和速度做一定的限制。一般情况下,将粒子的位置限定在区间[-Xmax,Xmax],而将粒子的速度限定在区间[-Vmax,Vmax]。

2.2算法的优化

虽然粒子群算法具有通用性强、收敛快等特点,但依然存在着容易早熟、后期迭代效率不高的问题,因此,本文从这2个方面入手对粒子群算法进行优化[9-10]。

导致粒子群算法出现早熟现象的原因是随着迭代过程的进行,种群搜索空间不断变小,因而容易陷入局部最优,而非全局最优的困境。参考遗传算法中的变异原理,将变异操作引入粒子群算法中,以达到在迭代过程中某些变量仍有一定概率重新初始化的目的。

变异操作实质上拓宽了计算时的种群搜索空间,在保持原有种群多样性的同时,提高了粒子群算法找到最优解的可能性。

针对粒子群算法后期迭代效率不高的问题,本文在基本算法的基础上通过优化惯性权重w来提高迭代效率。惯性权重表征的是粒子对先前速度的继承水平,很大程度上决定了粒子的进化速度(即迭代效率)。

研究表明,一个较大的惯性权重对全局搜索有利,而一个较小的惯性权重对局部搜索有利。为了充分发挥全局搜索和局部搜索各自的潜能,引入线性递减的惯性权重,即

(8)

其中,wstart为初始惯性权重;wend为迭代至最大次数时的惯性权重;k为当前迭代次数;Tmax为最大迭代代数。

2.3可靠指标求解的数学模型

使用粒子群算法计算结构可靠指标之前,首先需要建立适应粒子群算法的数学模型。X1,X2,…,Xn为结构可靠度分析中的n个独立随机变量,由它们表示的极限状态方程为g(X1,X2,…,Xn)=0,将非正态随机变量标准正态化,得到等效正态分布随机变量Z1,Z2,…,Zn。

本文根据可靠指标β的几何意义[11],将可靠指标β的求解问题转化为有约束条件的函数求极值问题。

目标函数为:

(9)

约束条件为:

(10)

其中,Z=(Z1,Z2,…,Zn)为标准化后的设计矢量。

2.4算法流程

得到结构可靠指标求解的数学模型后,便可运用粒子群算法进行计算。基于粒子群算法的可靠指标求解流程如图2所示。

图2　基于粒子群算法的可靠指标求解流程

3　钢管混凝土拱桥可靠度分析方法

通过BP神经网络拟合可得到结构极限状态函数,然后利用粒子群算法即可解得结构可靠指标。基于BP神经网络和粒子群算法的钢管混凝土拱桥可靠度分析过程如下:

(1) 确定钢管混凝土拱桥结构的随机变量及相应的统计特征,然后使用均匀设计法生成神经网络输入样本。

(2) 根据输入样本建立结构有限元模型,通过有限元软件进行结构确定性分析,得到神经网络输出样本(结构内力、位移等)。

(3) 对输入样本和输出样本进行归一化操作,将归一化后的样本代入神经网络进行学习,参照文献[12]的方法得到显式化的结构极限状态函数。

(4) 将非正态随机变量标准正态化,建立用于结构可靠指标求解的数学模型。

(5) 使用优化的粒子群算法最终求得结构可靠指标。

本文提出的用于钢管混凝土拱桥的可靠度分析方法是基于Matlab平台通过编程实现的。

4　算例验证

4.1计算过程

下面通过一个算例来验证本文方法的准确性和有效性,该算例为一下承式拱式平面结构,如图3所示。

结构计算跨径为10m,计算矢高为2.5m,拱轴线为二次抛物线,拱肋、主梁之间均匀布设8根吊杆,吊杆间距为1.11m,拱肋、吊杆及主梁均采用等截面的形式,主梁跨中受到一集中荷载P的作用。

图3　结构平面计算简图

取结构的随机变量为各构件的截面面积Ai、主梁惯性矩I和施加的外荷载P,相应的统计参数见表1所列。

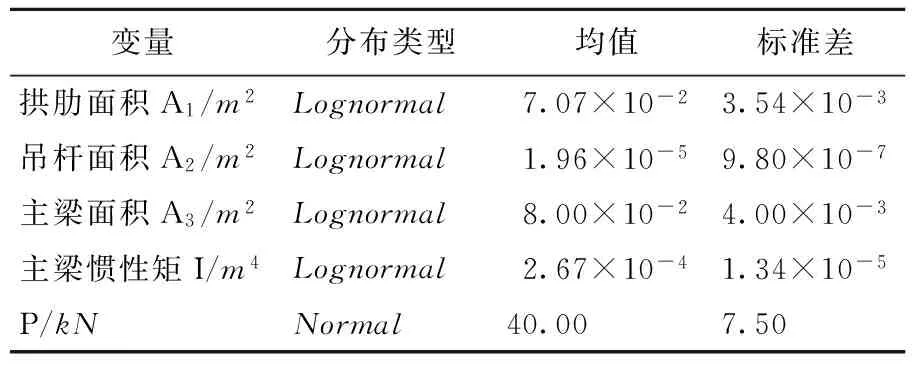
表1　随机变量统计参数

在正常使用极限状态条件下,主梁允许的最大竖向位移[u]=L/1 000=0.01m(L为计算跨径),由此建立结构的极限状态函数为:

(11)

为了对神经网络拟合的极限状态函数的准确性进行验证,随机生成20个验算点,然后进行结构有限元分析计算各点的真实极限状态函数值,并将其与神经网络拟合函数计算所得值进行对比,神经网络拟合的极限状态函数准确性验证结果如图4所示。

由图4可知,验算点的最大绝对误差不超过0.35%。结果表明,通过BP神经网络建立的结构显式化的极限状态函数具有良好的精度和预测能力,可以用来替代确定性的有限元分析。

图4　神经网络拟合的极限状态函数准确性验证结果

建立结构可靠指标求解数学模型后,使用优化的粒子群算法进行求解,可靠指标随着迭代次数增加的变化趋势如图5所示。

由图5可以看出,可靠指标值经过29代后趋于稳定。分别采用蒙特卡罗法、JC法和响应面法对结构进行可靠度分析,各方法对应的可靠指标、失效概率见表2所列。由于蒙特卡洛法是目前公认的精度最高的可靠度求解方法,因此将蒙特卡洛法的结果假定为真值。由表2可知,JC法与响应面法的求解精度较低,而本文的计算结果与蒙特卡洛法计算结果极为相近。考虑到蒙特卡罗法巨大的计算代价,本文提出的方法在不损失精度的前提下具有更强的实用价值。

图5　结构可靠指标随进化代数的变化趋势

可靠度计算方法失效概率可靠指标蒙特卡罗法0.008612.3821JC法0.010302.3152响应面法0.011082.2876本文方法0.008672.3795

4.2参数分析

BP神经网络拟合的极限状态函数的准确性直接影响着结构可靠指标的求解精度,是本文提出的钢管混凝土拱桥可靠度分析方法的关键。基于上述算例对影响BP神经网络拟合效果的2个主要参数(隐层神经元数目、样本数量)进行分析。

隐层神经元数目分别取5、6、7、8、9、10、11个,其余参数保持不变,构建相应的BP神经网络。将随机生成的20个验算点代入各个神经网络,用验算点的最大绝对误差比较极限状态函数的拟合精度,计算结果见表3所列。

表3　不同隐层神经元数目下验算点的最大绝对误差

由表3可知,隐层神经元数目对拟合精度有较大影响,当隐层神经元数目过少时,拟合效果较差;而隐层神经元数目过多时,出现神经网络过拟合的问题,反而降低了拟合精度。

采用相同的方法对样本数量进行分析,样本数量分别取60、70、80、90、100、110、120个，计算结果见表4所列。

表4　不同样本数量下验算点的最大绝对误差

由表4可知,样本数量较少时,拟合精度较差,当样本数量达到100个时,再增加样本数量对拟合精度的提高很小。

因此,使用本文方法进行可靠度分析时,推荐的样本数量为100个。

5　工程应用及分析

5.1工程概况

石门大桥是一座跨越319国道和石门水库的特大桥,大桥立面布置如图6所示。

图6　石门大桥立面布置

主桥采用中承式钢管混凝土拱桥,计算跨径248m,矢跨比为1/4,拱轴线为m=1.5的悬链线。单幅桥采用双片式拱肋,拱肋为钢管混凝土桁架式结构。

主桥采用横向双吊杆体系,吊杆采用OVM.GJ15-15拉索(1 860MPa钢绞线),全桥共设76根吊杆,吊杆纵向间距为10m。横梁通过吊杆与立柱和拱肋相连,横梁高度为2.2m。桥面系采用纵向“T”型行车道梁,形成全桥连续的纵、横向正交梁格体系。

5.2问题描述

在大跨径桥梁的计算分析中,结构几何非线性的影响通常不能忽略。为了探究正常使用状态下几何非线性对大跨径钢管混凝土拱桥可靠度的影响,使用有限元分析软件Ansys建立2种计算模型,模型1不考虑几何非线性的影响,模型2考虑几何非线性的影响。

建立有限元模型时,钢管混凝土结构通过节点

共单元的方式模拟,吊杆选用link180单元,其余结构均使用beam188单元建立。

考虑结构正常使用状态下的失效模式为位移失效模式,从位移限制准则的角度建立极限状态方程,因此结构极限状态函数可表示为:

(12)

其中,uL为活载作用下,规范规定的拱桥最大竖向允许位移[13],其值为L/1 000=248/1 000=0.248 m;x1,x2,…,xn为结构的随机变量。

合理确定随机变量及其统计参数是结构可靠度分析的关键,根据钢管混凝土拱桥正常使用状态下位移失效模式的特点,共选取10个随机变量。随机变量的均值由实桥图纸的设计参数确定,而随机变量的分布类型及变异性通过《公路工程结构可靠度设计统一标准》和现场调查确定。各随机变量及其统计参数见表5所列。

表5　结构主要随机变量统计参数

5.3求解及分析

由图7可知,不考虑几何非线性时,经过85代进化后结构可靠指标趋于稳定,对应的可靠指标β=4.816,此时失效概率pf=7.323×10-7;考虑几何非线性时,经过92代进化后结构可靠指标趋于稳定,对应的可靠指标β=4.537,此时失效概率pf=2.853×10-6。

图7　结构可靠指标随进化代数的变化

由上述分析可知,在正常使用极限状态下,大跨径钢管混凝土拱桥可靠度在考虑几何非线性情况下比不考虑几何非线性情况降低了6.15%。因此,在进行可靠度精确分析时,必须考虑几何非线性的影响。

6　结　　论

本文基于结构可靠度研究现状,将BP神经网络和优化的粒子群算法运用到钢管混凝土拱桥可靠度分析中,并对钢管混凝土拱桥正常使用极限状态下的可靠度进行研究,得到以下结论:

(1)BP神经网络在重构结构极限状态函数方面具有明显的优势。即使结构极限状态函数存在高度的非线性,BP神经网络仍能精确地逼近这种映射关系,极大地改善了传统响应面法的精度。

(2) 粒子群算法强大的极值寻优功能可以很好地适应复杂结构可靠指标求解的问题。计算结果表明,由粒子群算法计算的可靠指标与精确的蒙特卡罗法的求解结果极为接近,误差远远低于传统的JC法。

(3) 基于BP神经网络和粒子群算法的钢管混凝土拱桥可靠度分析结果表明,在正常使用极限状态下,几何非线性对大跨径钢管混凝土静力可靠度有较大影响,在进行静力可靠度精确分析时必须考虑几何非线性这一因素。

[1]桂劲松,康海贵.结构可靠度分析的全局响应面法研究[J].建筑结构学报,2004,25(4):100-105.

[2]董聪,刘西拉.非线性结构系统可靠性理论及其模拟算法[J].土木工程学报,1998,31(1):33-43.

[3]贡金鑫.结构可靠指标求解的一种新的迭代方法[J].计算结构力学及其应用,1995,12(3):369-373.

[4]RUMELHARTDE,HINTONGE,WILLIAMSRJ.Learninginternalrepresentationbyerrorpropagation[J].ParallelDistributedProcessing,1984(1):348-362.

[5]巩春领.大跨度斜拉桥施工期风险分析与对策研究[D].上海:同济大学,2006.

[6]方开泰,马长兴.正交和均匀实验设计[M].北京:科学出版社,2001.

[7]粟洪.大跨度悬索桥结构可靠度分析方法研究[D].上海:同济大学,2009.

[8]杨燕,靳蕃,KAMELM.微粒群优化算法研究现状及其进展[J].计算机工程,2004,30(21):3-4，9.

[9]RATNAWEERAA,HALGAMUGESK,WATSONHC.Self-organizinghierarchicalparticleswarmoptimizerwithtime-varyingaccelerationcoefficients[J].IEEETransactionsonEvolutionaryComputation,2004,8(3):240-255.

[10]梁军,程灿.改进的粒子群优化算法[J].计算机工程与设计,2008,29(11):2893-2896.

[11]张建仁,刘扬,徐福友.结构可靠度理论及其在桥梁工程中的应用[M].北京:人民交通出版社,2003.

[12]粟洪,程进.神经网络技术在预应力混凝土桥梁可靠度分析中的应用[J].结构工程师,2009,25(2):71-76.

[13]中华人民共和国住房和城乡建设部.钢管混凝土拱桥技术规范:GB50923—2013[S].北京:中国计划出版社,2013:26-27.

(责任编辑张镅)

ReliabilityanalysisofCFSTarchbridgesbasedonBPneuralnetworkandPSOalgorithm

CUIFengkun1,WANGHujun1,XUYue1,DONGFenghui2

(1.SchoolofHighway,Chang’anUniversity,Xi’an710064,China; 2.CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)

Inordertosolvethedifficultyofreliabilitycalculationforthelong-spanconcretefilledsteeltubular(CFST)archbridges,theBPneuralnetworkandparticleswarmoptimization(PSO)algorithmwereappliedtothereliabilityanalysisofarchbridges.Firstly,BPneuralnetworkwasusedtofitthelimitstatefunction,makingthehighlynonlinearlimitstateequationexplicit.ThenthePSOmethodwasusedtogloballysearchthedesignpointsandcalculatethereliabilityindex.TheanalysisresultsshowedthattheBPneuralnetworkandPSOalgorithmmadeupforthedeficiencyofthetraditionalreliabilityanalysismethodsandimprovedthecalculationaccuracy,thusprovidinganewthoughtandmeansforthestudyofthereliabilityoflong-spanbridges.

concretefilledsteeltubular(CFST)archbridge;BPneuralnetwork;particleswarmoptimization(PSO)algorithm;reliability;reliabilityindex

2015-03-25；

2015-06-11

国家自然科学基金资助项目(50808019);国家留学基金委资助项目(201606560011)

崔凤坤(1990-),男,山东潍坊人,长安大学博士生;

徐岳(1958-),男,陕西乾县人,博士,长安大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.08.020

U448.22

A

1003-5060(2016)08-1103-07