基于能量抗震设计地震动强度指标研究

陆　松,　王德才,　叶献国

(1.合肥工业大学 土木与水利工程学院,安徽 合肥　230009; 2.合肥工业大学 建筑与艺术学院,安徽 合肥　230601)



基于能量抗震设计地震动强度指标研究

陆松1,王德才2,叶献国1

(1.合肥工业大学 土木与水利工程学院,安徽 合肥230009; 2.合肥工业大学 建筑与艺术学院,安徽 合肥230601)

文章选择694条不同场地类型的地震动记录作为地震动输入,计算了弹性和弹塑性单自由度体系和6个不同自振周期的多自由度结构能量反应;提出表征地震动输入能量特征的强度指标Ie,对该指标和14个已有强度指标与结构能量反应的相关性进行了分析。结果表明:与速度有关的强度指标和结构能量反应之间具有较高的相关性;对于不同周期结构,强度指标Ie与结构能量反应之间均具有较好的相关性,可以作为较合理的地震动强度指标用于基于能量抗震设计方法。

输入能量;强度指标;滞回耗能;地震动

地震动强度指标建立了结构地震反应和地震能量输入之间的联系,是衡量地震作用的关键参数,不同的抗震设计方法都需要采用综合考虑地震动特征的参数来反映地震动强度。但是,由于地震动的复杂性和影响因素众多,目前并没有一个较好的强度指标可以综合反映地震动特征[1]。因此,合理选择表征地震动特性的地震动强度指标用于结构抗震设计与性能分析具有重要意义,也是地震工程领域研究的热点[2]。

在基于性能的抗震设计方法中常采用承载力、位移等指标进行设计,但只有能量指标可以反映结构的累积损伤。基于能量抗震性能评估方法在近年来也得到了较快发展,并初步形成了基于能量抗震设计方法[3]。尤其对于日益增多的减隔震结构体系,由于结构中布置了耗能装置,能量方法相比于其他评价方法更为合适。为了建立合理的强度指标来反映地震动的相关能量输入，并进行基于能量的抗震设计,本文首先根据地震动输入特征提出了反映地震动能量特征的复合强度指标Ie,选择不同场地特征下的地震记录694条,对包括Ie在内的15个不同地震动强度指标之间及15个指标与单自由度和多自由度结构体系能量反应结果之间的相关性进行分析,验证了提出的强度指标Ie应用于抗震设计的合理性。

1　地震动记录的选择

从太平洋地震工程中心(Pacific Earthquake Engineering Research Center,PEER)地震动记录数据库和欧洲及中东地面运动记录光盘数据库(Strong-Motion Datascape Navigator,SMDN)中选取地震动记录。其中,PEER数据库涵盖了各国的经过统一数据处理的地震动记录;SMDN由经过校正处理的462条强震记录组成,主要选自欧洲强震记录数据库,并且含有一些仪器台站的完备钻孔资料[4-5]。

以文献[6]规定的划分场地类别的方法为依据,并参考文献[7]中对30 m剪切波速与我国抗震规范对场地类型的划分标准之间的关系研究,从上述数据库中共选取了694条不同场地类型的地震动记录,其中Ⅰ0和Ⅰ1类场地记录193条,Ⅱ类和Ⅲ类场地记录分别为310条和191条,由于Ⅳ类场地的地震记录很少,未选择对应记录。为了使选择的记录反映破坏性地震的特征并具有一定的工程意义,选取的地震动记录同时满足以下5个条件:① 地震震级不小于4级;② 峰值加速度不小于20 cm/s2;③ 自由地表取得的记录;④ 场地条件明确;⑤ 同一组记录中只选择1条水平方向记录。选取的地震动的震级与震中距分布如图1所示。

图1　选取的地震动记录的震级与震中距分布

从图1中可以看出,选取的694条地震动记录的震级主要在5.6～8.0级范围内,震中距主要分布在10～150 km之间,因此,这些地震动记录符合破坏性特征的要求,并且震中距的范围也具有代表性。

2　不同强度指标及其相关性

不同研究者根据具体研究目的已提出了大量强度指标,主要有以下3种。

(1) 峰值参数。该类指标有峰值地面运动加速度(PGA)、峰值地面运动速度(PGV)和峰值地面运动位移(PGD)。

(2) 基于地震动时程本身的能量和复合参数。该类指标包括均方根加速度(arms)、均方根速度(vrms)、最大增量速度(MIV)、Arias强度(Ia)、累积绝对速度(CAV)、表征地面运动潜在破坏势参数[8]Pd、表征地震动对中长周期结构影响的参数[9]If以及可表征结构地震作用下损伤程度的地震动参数[8-9],即特征强度Ic。

(3) 基于弹性反应谱值的参数。该类指标包括速度谱强度(VSI)、有效峰值加速度(EPA)以及有效峰值速度(EPV)[10]。

本文提出表征地震动输入能量特征的强度指标Ie,计算公式为:

(1)

其中,V为峰值地面运动速度(PGV);A为峰值地面运动加速度(PGA);a(t)为加速度时程;Dr为地震总持时。

(1)式由文献[11]提出的计算输入能量公式演化而来,即将原式中的卓越周期用PGV与PGA的比值(V/A)替换,使表达式的计算更为方便简单,且同样反映了输入能量特征。该强度指标考虑了频谱特性,同时也反映了地震持时的特性。文献[12]认为卓越周期在一般的地震中并不明显,同时Newmark-Hall弹性谱中的等加速度段与等速度段的交点所对应的过渡周期值通常被认为可以代表地面运动的卓越周期,而V/A与该过渡周期值之间具有较明显的相关性,所以在(1)式中将卓越周期用V/A替代。近年来的地震工程研究发现，不同地面运动的峰值加速度、速度的差异与地震波的频谱特性有直接关系,高频波主要影响地面运动峰值加速度,而中低频则主要影响峰值速度。

随着断层距的增加,地震波中的高频成分将很快被过滤,导致PGV与PGA的比值迅速减小。因此,震源距大的地面运动的V/A值将明显高于震源距小的地面运动的V/A值,远震通常具有长持时和长特征周期,而近震通常具有短持时、高频和脉冲型的特征。因此,在一定程度上,可以根据参数V/A的值来确定地面运动的持时和频谱特性。文献[13]发现,从小震和中震的附近地区获得的地震动记录大部分具有较小的V/A值,而从大震中离震源较远地区获得的记录具有相对较高的V/A值,一般前者的能量主要集中在短周期范围内,而后者的地震波能量主要集中在长周期范围内。

本文以上述15个指标作为分析对象。

3　与单自由度体系能量反应相关性

以选取的694条地震记录作为输入,以周期范围为0.05～6 s、阻尼比为5%的单自由度体系作为分析对象。为了确定不同周期结构的输入能量与上述15个指标之间的相关性,计算它们的相关性系数。

弹塑性单自由度体系以理想弹塑性模型为恢复力模型,延性系数分别取1、2、4和6。通过弹性和弹塑性时程分析得到各不同延性结构在各条地震动下的地震能量反应谱。然后计算各强度指标与输入能量之间的相关系数,进而得到不同强度指标与不同延性比结构的输入能量之间的线性相关系数谱,如图2所示。

通过计算上述15个强度指标与结构输入能量之间的相关系数谱,发现在大部分周期范围内,与地面运动速度有关的强度指标与输入能量的相关性较高,这是因为地面运动速度通常与能量之间有很密切的联系,这个结论已被相关文献[8-9,11]证明。只有在短周期段,与加速度有关的强度指标与输入能量之间才具有较好的相关性。

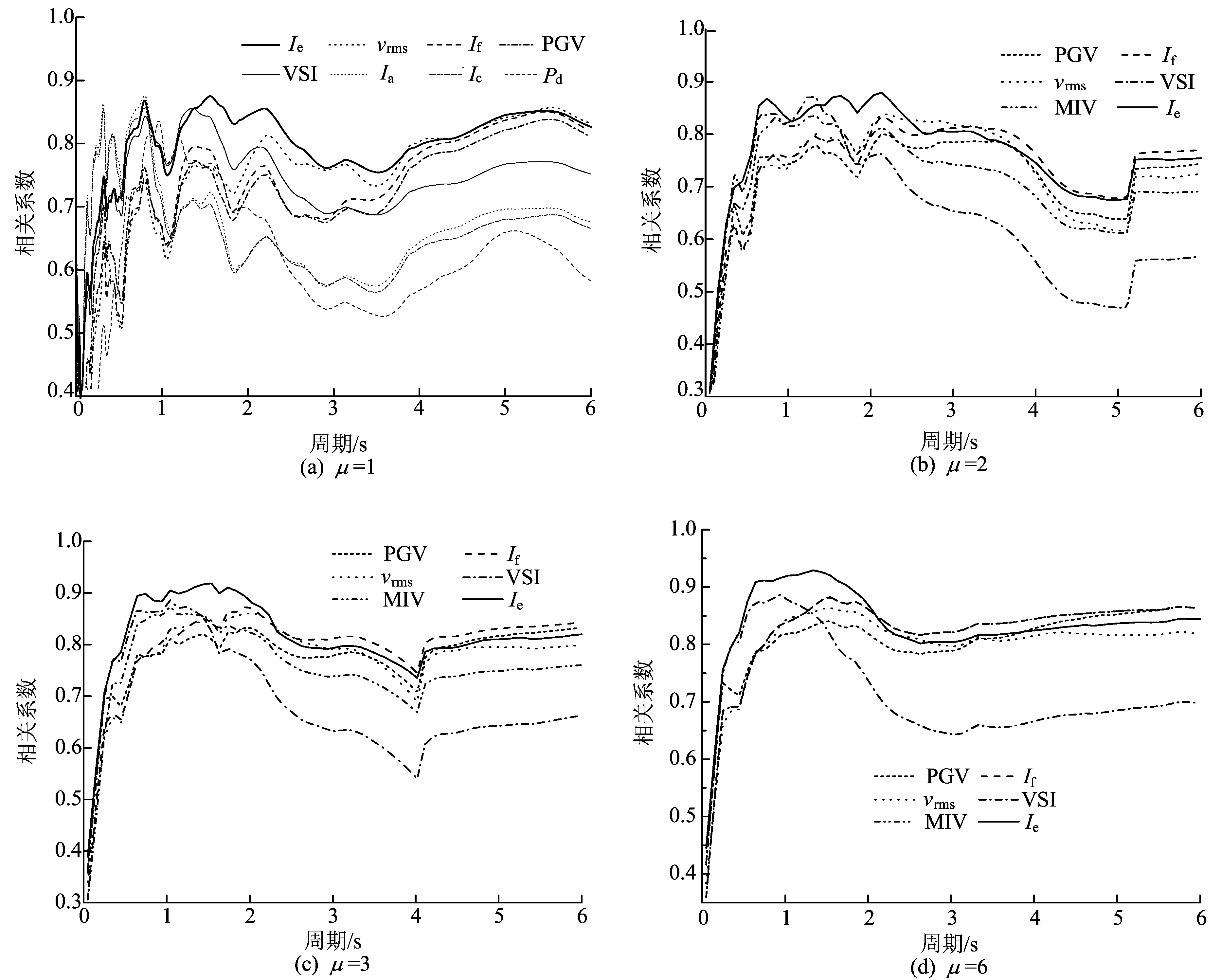
图2　地震动强度指标与输入能量之间的相关系数谱

不同周期的弹性体系的输入能量与相关性较好的8个强度指标之间的相关系数谱如图2a所示。Ia、Ic和Ie与输入能量的相关性在短周期范围内较高;Ie、vrms和VSI与输入能量在0.6～2.5 s范围内相关性较高;vrms、If和Ie的相关性在长周期范围内较高,并且这3个参数相差不大。本文提出的强度指标Ie的相关系数值在短周期范围内仅较低于Ia和Ic,但在中长周期范围内Ia和Ic的相关系数值较小。VSI在中等周期范围内的相关系数值较大,但是在长周期段较小,并且低于其他大部分参数的相关系数值。在长周期段,Ie的相关系数值较低于If和vrms,但是在中短周期范围内Ie的相关系数值则大于If和vrms。通过分析弹性体系的输入能量与各强度指标的相关性,可以看出参数Ie在整个周期范围内可以较好地代表体系的输入能量。

延性分别为2、4和6的单自由度体系的输入能量与相关性较好的6个强度指标的相关系数谱如图2b～图2d所示,可以发现与结构输入能量相关性较高的强度指标在不同延性结构中变化不大,分别是PGV、If、vrms、VSI、MIV和Ie。其中,在整个周期范围内Ie与输入能量总体上相关性最好。6个强度指标与输入能量的相关性在短周期段随着周期的增加,总体呈上升趋势;在中等周期段达到最大;随后在长周期段略有减小。通过对比图2b～图2d发现,随着结构延性的增加,相关性也大致呈上升趋势。

通过分析上述6个强度指标与延性分别为1、2、4、6的单自由度体系的能量输入之间的相关性可知,各不同延性结构体系的输入能量在整个周期范围内通常与那些和速度相关的强度指标具有较高的相关性,其中Ie与输入能量相关性最高。

4　与多自由度体系能量反应相关性

采用层数分别为2、5、10、15、20和30层的6个剪切型结构作为分析模型,它们相应的基本周期分别为0.2、0.5、1.0、1.5、2.0、3.0 s,质量沿楼层均匀分布,结构体系沿竖向规则。令各层的屈服剪力系数ξy都等于0.33,这可以避免在某些楼层产生能量集中,使得多自由度系统产生以整体行为为主的地震响应。屈服承载力由(2)式确定,即

(2)

其中,Fyi为第i层的屈服承载力;Fei为通过对结构进行弹性时程分析得到的第i层的弹性承载力;ξy为屈服剪力系数。采用双线性模型表示层间力-位移滞回关系,屈服后刚度比取0.05。

从694条记录中选择40条地震动记录进行分析,首先将它们的PGA调整为400 cm/s2。通过对各弹性结构的时程分析获得它们的弹性总输入能量和弹性层间剪力,再根据(2)式获得对应的屈服剪力;然后进行相应的弹塑性时程分析得到它们的输入能量和各层层间的滞回耗能。

计算不同强度指标与结构弹塑性总输入能量、总滞回能量及各层层间滞回耗能之间的Pearson相关系数,6个相关性较高的强度指标与上述3个能量项之间的相关系数图分别如图3和图4所示。

从图3a可以看出,参数Ie与弹塑性总输入能量的相关性要高于其他参数;同时各指标的相关系数值在短周期段较小,在1 s后基本保持不变。因为在相同的阻尼比下,各不同基本周期结构的总滞回能量与总输入能量的比值变化很小,从图3b可见,与总滞回耗能相关性较高的强度指标也分别为Ie、If和vrms。

图3　强度指标与多自由度结构能量反应参数的相关性

为了便于比较不同结构层间滞回耗能与各强度指标之间的相关性,定义楼层指数Is为:

(3)

其中,n为对应的楼层数;N为总层数。由(3)式可知,第1层Is为0,第N层Is为1。2、5、10、20层结构的层间耗能与强度指标之间的相关性如图4所示。

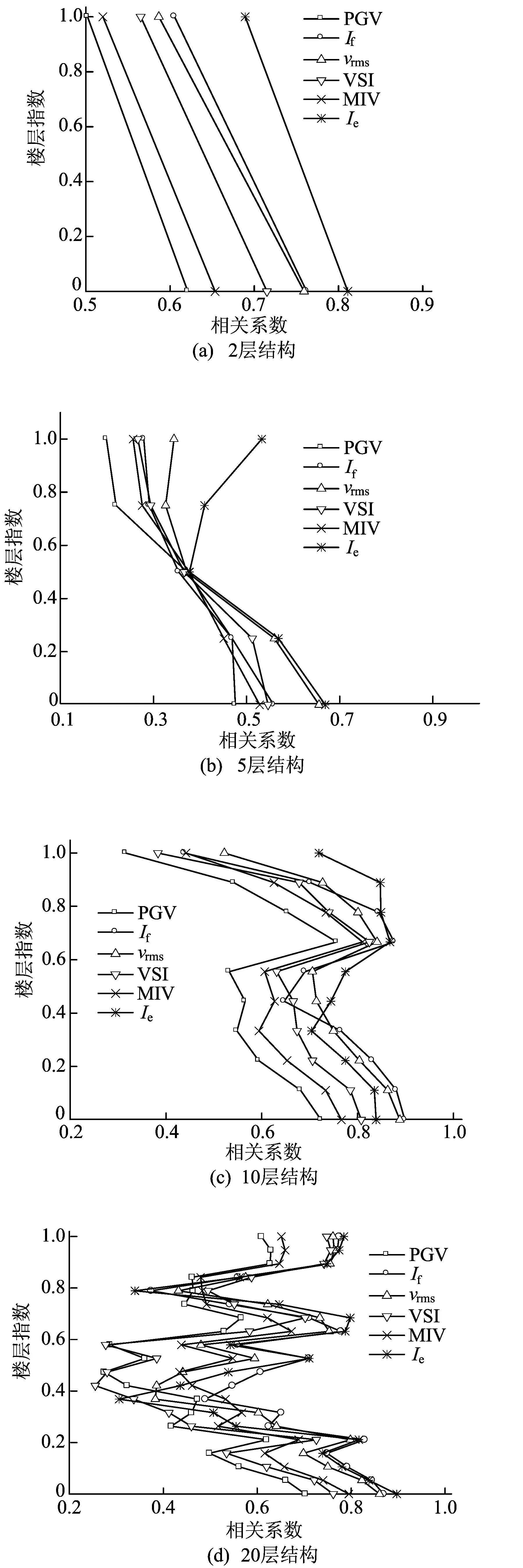
图4　强度指标与多自由度结构层间耗能之间相关性

对于2层和5层的短周期结构,Ie、If和vrms与各层耗能的相关系数值较大；其中Ie相关性最高。对于10层的中等周期结构,If、vrms和Ie与各层层间耗能相关系数值较大；其中在1～4层,If与各层耗能相关性最好;在4层以上,相关性最好的参数则交替变换。对于20层的较长周期结构，仍然是Ie、If和vrms与层间耗能相关性较好,尽管对于个别楼层,上述3个参数的相关系数可能较小。

对不同基本自振周期的弹塑性多自由度结构模型的能量反应与不同强度指标相关性的分析表明,与速度有关的强度指标Ie、If和vrms与结构的总输入能量、总滞回能量以及各层的层间滞回耗能相关性较好,其中总体上相关性最好的为Ie。

5　结　　论

本文对基于能量抗震设计合理选取地震动强度指标开展了研究,以已有的14个强度指标和本文提出的1个强度指标作为分析对象,从PEER和SMDN地震动记录数据库中选择了不同场地类型的694条记录作为地震动输入,通过单自由度和多自由度体系结构能量反应参数与不同强度指标的相关性分析,确定较合理的地震动强度指标,得到了以下结论:

(1) 与结构能量反应之间具有相对较高相关性的指标通常为与速度有关的地震动参数。

(2) 对弹性和不同延性的弹塑性单自由度体系输入能量与不同强度指标相关性的分析表明,Ie的相关性在整个周期范围内整体上较好,仅在短周期范围内小于个别参数。

(3) 对不同基本周期的弹塑性多自由度结构模型的能量反应与不同强度指标相关性的分析表明,各能量参数与Ie的相关性均较好,强度指标If和vrms的相关性也较好。

通过分析不同的强度指标与单自由度结构体系和多自由度结构体系的总输入能量和滞回能量的相关性,发现本文提出的复合强度指标Ie相关性较好,可以作为基于能量抗震设计的地震动强度指标。

[1]叶献国.地震强度指标定义的客观评价[J].合肥工业大学学报(自然科学版),1998,21(6):7-11.

[2]叶列平,马千里,缪志伟.结构抗震分析用地震动强度指标的研究[J].地震工程与工程振动,2009,29(4):9-22.

[3]SURAHMAN A.Earthquake-resistant structural design through energy demand and capacity[J].Earthquake Engineering & Structural Dynamics,2007,36(14): 2099-2117.

[4]POWERM,CHIOUB,ABRAHAMSONN,etal.AnoverviewoftheNGAproject[J].EarthquakeSpectra,2008,24(1):3-21.

[5]AMBRASEYSNN,DOUGLASJ,SIGBJOMSSONR,etal.DisseminationofEuropeanstrong-motiondata,Vol2,usingStrong-MotionDatascapeNavigator[C/OL]//13thWorldConferenceonEarthquakeEngineering,Vancouver,B.C.,Canada,August1-6.[S.l.:s.n.],2004.PaperNo. 32.(2004-07-13)[2015-03-10].http:www.iitk.ac.in/nicee/wcee/article/13-32.pdf.

[6]中华人民共和国住房和城乡建设部.建筑抗震设计规范:GB50011—2010[S].北京：中国建筑工业出版社，2010：19-21.

[7]吕红山,赵凤新.适用于中国场地分类的地震动反应谱放大系数[J].地震学报,2007,29(1):67-76.

[8]ARAYAR,SARAGONISR.Earthquakeaccelerogramdestructivenesspotentialfactor[C]//Proceedingsofthe8thWorldConferenceonEarthquakeEngineering,SanFransisco：EarthquakeEngineeringResearchInstitute,1984:835-842.

[9]FAJFARP,VIDICT,FISCHINGERM.Seismicdemandinmediumandlong-periodstructures[J].EarthquakeEngineering&StructuralDynamics,1989,18(8):1133-1144.

[10]NAUJM,HALLWJ.Scalingmethodsforearthquakeresponsespectra[J].JournalofStructuralEngineering,1984,110(7):1533-1548.

[11]KUWAMURAH,GALAMBOSTV.Earthquakeloadforstructuralreliability[J].JournalofStructuralEngineering,1989,115(6):1446-1462.

[12]FAJFARP,VIDICT.Consistentinelasticdesignspectra:hystereticandinputenergy[J].EarthquakeEngineering&StructuralDynamics,1994,23(5):523-537.

[13]TSOWK,ZHUTJ,HEIDEBRECHTA.EngineeringimplicationofgroundmotionA/Vratio[J].SoilDynamicsandEarthquakeEngineering,1992,11(3):133-144.

(责任编辑张淑艳)

Ground motion intensity measures for seismic design method based on energy

LU Song1,WANG Decai2,YE Xianguo1

(1.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China; 2.School of Architecture and Art, Hefei University of Technology, Hefei 230601, China)

Using 694 ground motion records with different soil conditions as ground motion input, the energy responses of elastic and inelastic single degree-of-freedom(SDOF) system and six multi-degree-of-freedom(MDOF) structures with different vibration periods are calculated. The correlation analysis is conducted on 14 existing intensity measures and the proposed measureIein this paper with the energy responses of the above structures. The results show that the correlation between the velocity related intensity measure and the energy responses of structures is relatively high; for the structures with different periods, the better correlation between the proposed measureIeand the energy responses is found, and this measure can be used as the ground motion intensity measure for seismic design method based on energy.

input energy; intensity measure; hysteretic energy; ground motion

2015-03-23；

2015-05-14

国家自然科学基金资助项目(51378167)

陆松(1991-),男,安徽长丰人,合肥工业大学硕士生;

叶献国(1954-),男,安徽无为人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.08.018

TU352.11

A

1003-5060(2016)08-1093-06