伪弹性形状记忆合金梁弯曲特性研究

崔世堂,　刘淑莉，　王　波，　张　科

(1.中国科学技术大学 中国科学院材料力学行为和设计重点实验室,安徽 合肥　230026； 2.陆军军官学院 四系,安徽 合肥　230031)



伪弹性形状记忆合金梁弯曲特性研究

崔世堂1,2,刘淑莉2，王波1，张科1

(1.中国科学技术大学 中国科学院材料力学行为和设计重点实验室,安徽 合肥230026； 2.陆军军官学院 四系,安徽 合肥230031)

基于理想伪弹性形状记忆合金的非线性应力应变关系,文章对形状记忆合金(shape memory alloy,SMA)梁在纯弯曲载荷作用下的力学行为进行了研究；给出了加卸载过程中应力、弯矩和曲率之间的解析表达式,弯矩曲率关系呈现明显的非线性滞回特性；揭示了梁截面上各相的发展演化以及相边界的运动规律。在加载阶段相边界均随弯矩的增大向中性层移动,而在卸载阶段相边界的变化规律不仅与加载结束时表层材料所处的状态有关,还与卸载的程度有关,表现出与加载阶段完全不同的特性。

形状记忆合金;纯弯曲;相变;弯矩曲率关系

形状记忆合金(shape memory alloy,SMA)是一类特殊的兼有功能性和结构强度的智能材料,近年来已受到材料科学和工程界的重视,在机械、航天及医学等领域逐步得到应用。其最引人注目的2个特性是伪弹性(pseudo-elastic,PE)和形状记忆效应(shape memory effect,SME),其变形和吸能的物理机制在于热弹性奥氏体相和马氏体相的相互转化[1-2]。当材料处于形状记忆状态时,在经历较大变形后会留下残余变形,只要适当加热,变形即可恢复;材料处于伪弹性状态时,当加载应力超过某一临界值,将产生应力诱发马氏体相变,相变结束后,材料由奥氏体相转变成马氏体相。材料卸载达到另一临界值时将诱发马氏体相变,材料重新转变成奥氏体相。加卸载的过程并不重合,应力应变曲线具有较大的滞回,但卸载后无残余变形,呈现出和普通弹塑性材料截然不同的特性。目前对于SMA梁的研究主要集中在准静态,文献[3]从理论上研究了伪弹性SMA梁的弯曲问题,给出了在单弯矩脉冲作用下矩形截面梁的弯矩曲率表达式。文献[4-5]研究了2个数值计算程序来确定梁截面的响应,并采用有限元方法模拟了三点弯曲和四点弯曲实验,数值计算结果和实验非常接近。文献[5]建立了一维本构模型,考虑了热力耦合作用并借助于有限元方法对纯弯曲问题进行求解。文献[6]通过实验和数值方法研究了加载过程中SMA丝的弯曲问题。文献[7]通过实验和数值方法研究了SMA梁的弯曲问题,目的在于验证其提出的相变函数。在上述研究中,更多关注的是伪弹性状态下SMA梁的变形以及梁截面上应力分布等问题。而在加卸载过程中,梁截面上相边界处的应力梯度存在间断,截面上会由于材料的相变演化形成运动的相边界,对相边界的运动规律以及各相之间的演化等问题的研究相对不多。

本文以理想伪弹性SMA梁为研究对象,通过引入平截面假定,研究了纯弯曲情况下矩形截面梁的弯曲特性。以曲率为基本未知量,得到了加卸载阶段截面上的应力和弯矩分布的解析表达式,并通过数值算例揭示了加卸载过程中梁截面上各相的演化以及相边界的运动规律。

1　形状记忆合金的本构关系

理想伪弹性SMA的应力应变关系如图1所示。

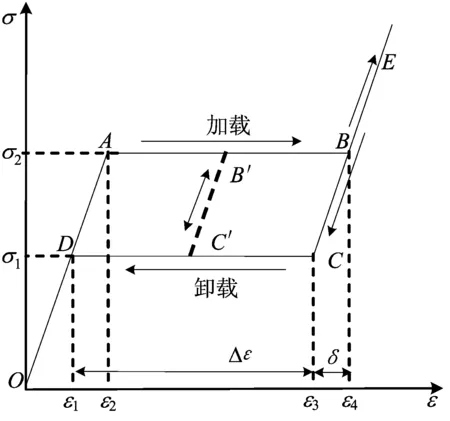
图1　理想伪弹性SMA的应力-应变曲线

在加载阶段,奥氏体相开始向马氏体相转变的起始应力和应变分别为σ2=465 MPa和ε2=0.75%(A点),奥氏体相完全转化为马氏体时的应力和应变分别为σ2=465 MPa和ε4=4.75%(B点);在卸载阶段,如果卸载开始时的应变ε>ε4,逆相变开始时的应力和应变分别为σ1=186 MPa和ε3=4.3%(C点),逆相变结束时的应力和应变分别为σ1=186 MPa和ε1=0.3%(D点)。如果加载结束时的应变为εB′(B′点),卸载后应变沿着B′C′降至εC′(C′点)后开始发生逆相变,沿C′D和DO回到原点。为简化起见,假设奥氏体相和马氏体相的弹性模量均为E,弹性卸载段和弹性加载段斜率相同,即图1中OA∥B′C′。

2　加载阶段的应力分布和弯矩曲率关系

假设矩形截面梁的宽度为B,高度为2H,如图2所示。

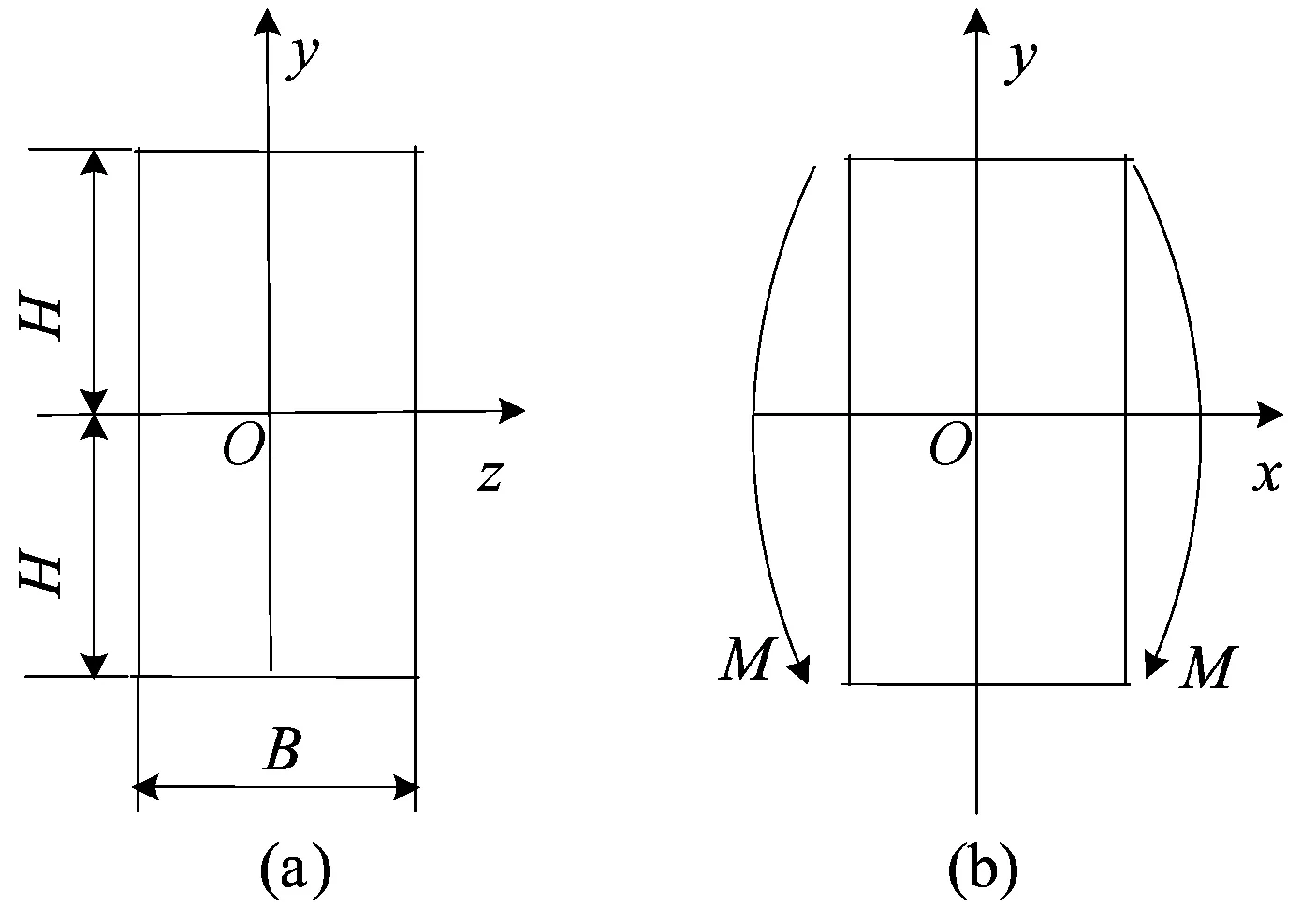
图2　梁微元段弯曲示意图

在纯弯曲加卸载过程中始终满足平截面假定[8],根据经典的梁理论,离开中性层的距离为y处的应变如下:

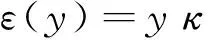
(1)

其中,κ为截面中性层的曲率。

记λ1=ε4/ε2,λ2=ε3/ε1,当截面表层材料的应变分别为ε1、ε2、ε3、ε4时,定义其曲率分别为:

(2)

根据平截面假定,在整个加卸载过程中截面表层材料的应变始终最大,且在纯弯曲的情况下,梁截面上材料处于单向拉伸或者单向压缩状态,考虑到截面的几何形状、受力状态与材料的应力应变曲线的对称性,仅对受拉侧进行分析。在加载过程中,总是表层材料率先发生相变或相变完成,因此表层材料处于奥氏体相(0≤κ<κ2)、混合相(κ2≤κ<κ4)和马氏体相(κ4<κ)。

2.1奥氏体相阶段

梁整个截面上材料始终为奥氏体相,并没有相变发生,截面上的应力分布如图3a所示。

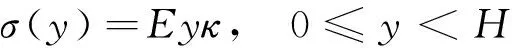
(3)

随截面上的弯矩不断增大,表层材料的应变首先达到ε2,弹性阶段结束。

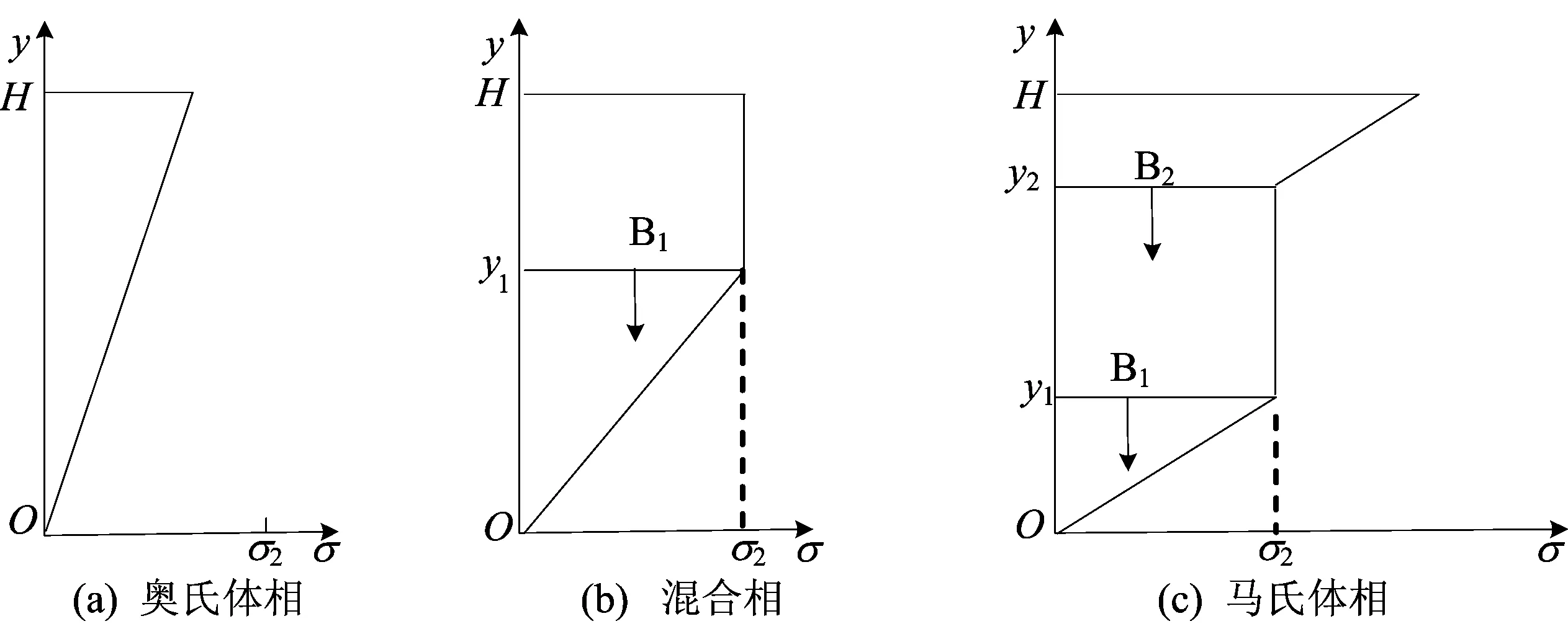
图3　加载过程中的应力分布

2.2混合相阶段

表层材料开始相变,相变区自表面向中心扩展,此时截面上中心部分材料处于奥氏体相,外层材料处于奥氏体相和马氏体相的混合状态,奥氏体相区和混合相区之间存在一个相边界B1,如图3b所示。当表层材料的应变达到ε4时,表层材料已完全转化为马氏体相,第2阶段结束。设相边界的高度为y1,相边界处的应变为ε2,可得:

(4)

由(4)式可见,随着截面弯曲变形(κ)的增大,相边界的高度减小,即相边界B1向中性轴方向移动,图3b中的箭头代表相边界移动的方向。截面上应力的分布为:

(5)

2.3马氏体相阶段

截面表层材料相变完成,完全处于马氏体相。截面中心向外分别为奥氏体相区、混合相区和马氏体相区。在奥氏体相区和混合相区、混合相区和马氏体相区的界面上存在2个相边界B1和B2,如图3c所示。设相边界B1和B2的高度分别为y1和y2,y1处的应变为ε2,y2处的应变为ε4,由应变和曲率之间的关系可得相边界的高度如下:

(6)

截面上的应力沿高度的分布表达式为:

(7)

截面上的平衡条件为:

(8)

将(3)式、(5)式和(7)式分别代入(8)式,可得加载阶段的弯矩曲率关系为:

(9)

其中,I为梁截面的惯性矩。

3　卸载阶段的应力分布和弯矩曲率关系

设加载结束时梁中性轴的曲率为κi,当0≤κi<κ2时，整个截面处于弹性变形,截面上的应力分布如图3a所示,卸载后的弯矩M为:

(10)

当κ>κ2时,表层材料已发生相变或相变完成,从不同的阶段进行卸载,卸载的路径完全不同。以下对κ2≤κi<κ4和κi>κ42种情况进行讨论。

3.1κ2≤κi<κ4

加载结束时,相边界B1的高度为：

(11)

截面上的应力分布如图3b所示。根据卸载阶段截面上材料的相变特性分为4个阶段。

(1)κi-(δ/H)<κ<κi。卸载开始后,截面上的应力和应变线性减少,并与截面高度呈正比,因此表层材料应变降得最快,当表层材料的应变减小δ时,表层材料最先到达逆相变的临界点,而其余位置并没有逆相变发生,此时截面中性轴的曲率减小δ/H,而相边界B1处的应变减小量Δε<δ,逆相变还没有开始,因此相边界并没有移动，此时的应力分布如图4a所示,截面上的应力分布表达式为:

(12)

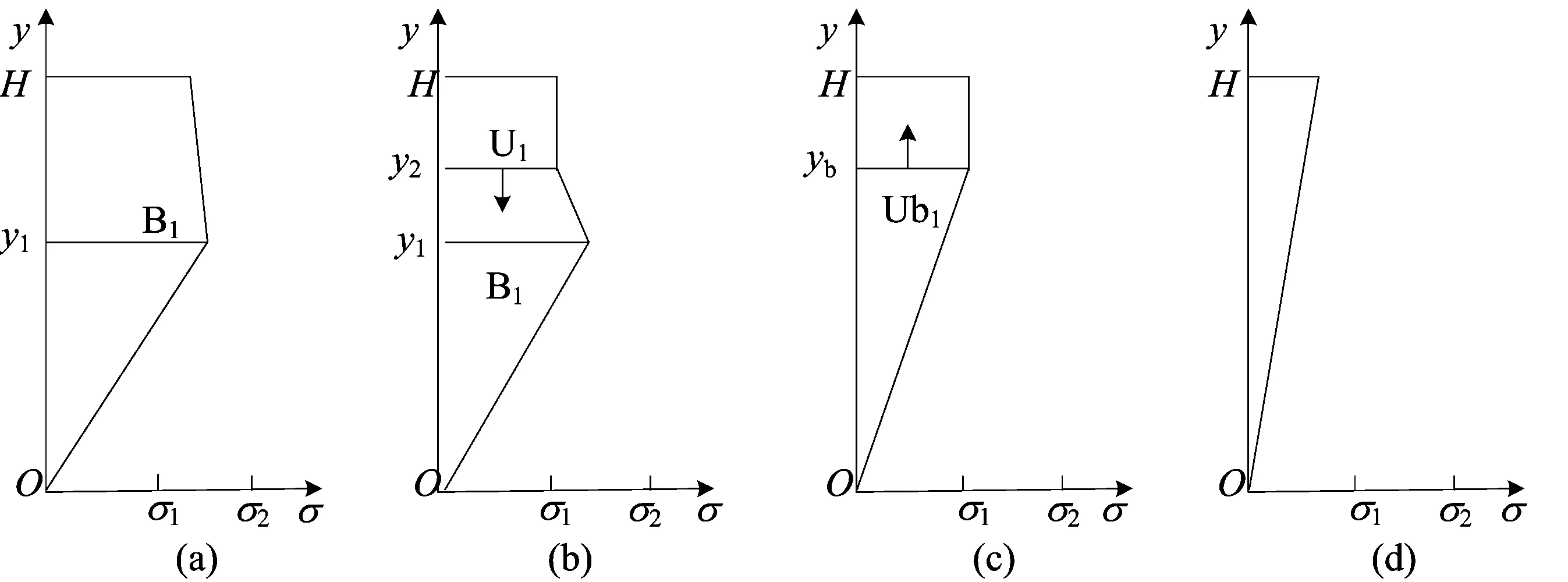
图4　κ2≤κi<κ4时卸载阶段的应力分布

(2) (κ1κi/κ2)≤κ<κi-(δ/H)。随着截面曲率的减小,表层材料开始发生逆相变,在逆相变区和混合相弹性卸载区之间出现一个向中心发展的卸载相边界U1,如图4b所示。B1和U1之间的材料进行弹性卸载,并没有发生逆相变,相边界B1的高度不变。直到相边界B1处的材料达到逆相变的临界点,卸载相边界U1和相边界B1重合,此时截面中性轴的曲率降为κ1κi/κ2。设卸载相边界U1的高度为y2,此处的应变减小了δ,根据应变和曲率的关系可得:

(13)

截面上的应力分布表达式为:

(14)

(3)κ1≤κ<(κ1κi/κ2)。整个混合相区都在发生逆相变,相边界B1消失,出现1个新的向表层移动的卸载相边界Ub1,如图4c所示。直至移动到梁的表层,该阶段结束,结束时中性轴的曲率降为κ1。设卸载过程中相边界Ub1的高度为yb,此处的应变为ε1,根据应变和曲率的关系可得:

(15)

截面上的应力分布表达式为:

(16)

(4) 0≤κ<κ1。截面上材料逆相变完成后,材料处于奥氏体相,相边界消失,截面上应力分布如图4d所示。截面上的应力分布表达式与 (3) 式相同。

3.2κi>κ4

当加载结束时中性轴的曲率κi>κ4时,截面表层材料已经相变完成,完全处于马氏体相,截面上的应力分布如图3c所示。根据卸载截面上材料的相变特性分为5个阶段。

(1) (κ1λ2/κ2λ1)κi<κ≤κi。卸载开始后,奥氏体相区、混合相区和马氏体相区的应力和应变线性减小,但逆相变没有开始,相边界的位置并没有发生变化,截面上应力的分布如图5a所示。

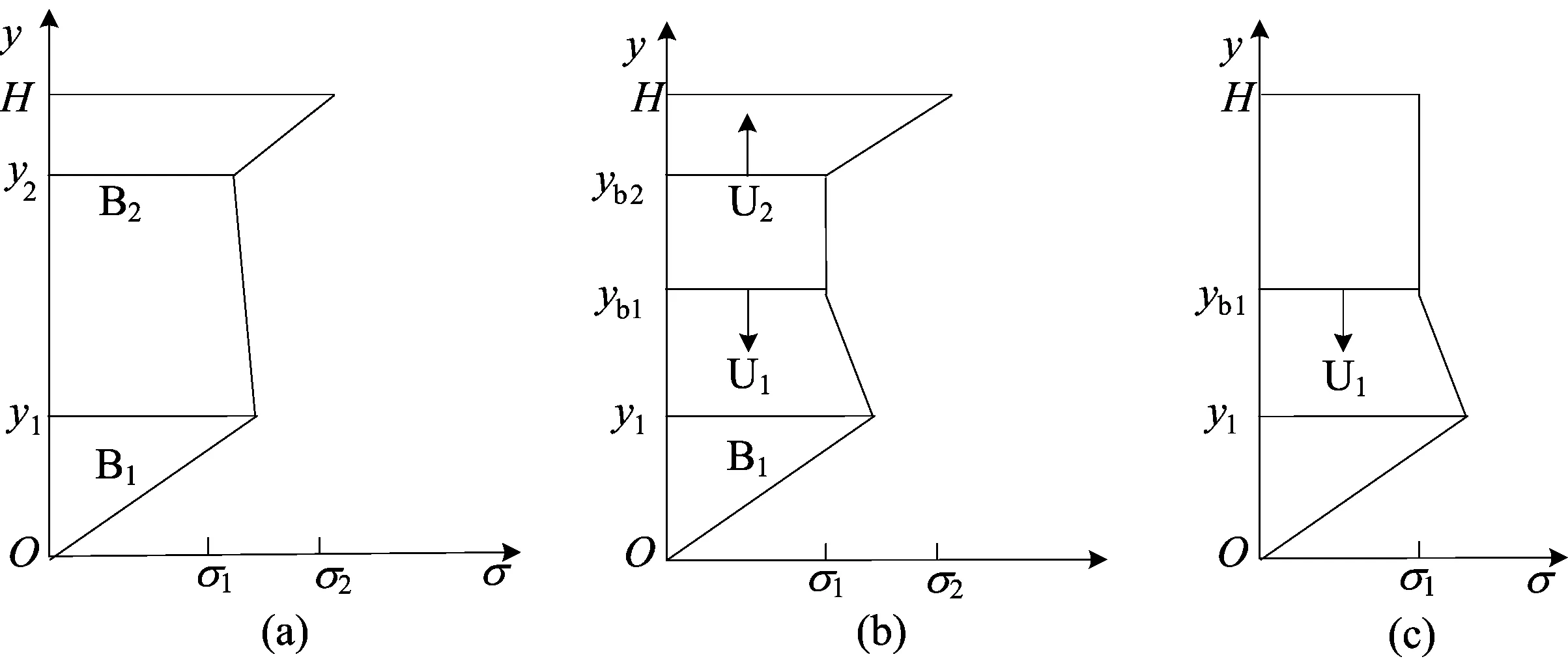
图5　κi>κ4卸载阶段应力分布

相边界B2处的应变为ε4,当该处的应变减小δ降为ε3时,y1和y2之间的混合相区的应变减小量Δε均小于δ,混合相区仅发生弹性卸载,并没有发生逆相变。根据平截面假定,马氏体相区的应变ε(y)均大于ε3,即马氏体相区也没有发生逆相变,因此卸载过程的逆相变首先是从相边界B2处开始。

当相边界B2处开始发生逆相变时,梁截面中性轴的曲率降为(κ1λ2/κ2λ1)κi。截面上应力的分布表达式为:

(17)

(2)λ2κ1<κ≤(κ1λ2/κ2λ1)κi。逆相变在y2处发生后,相边界B2消失,形成两条向两侧发展的卸载相边界U1和U2,如图5b所示。此时截面上自中性轴向外依次为奥氏体相区、未发生逆相变的混合相区、已发生逆相变的混合相区和马氏体相区。当相边界U2达到梁表面时,该阶段结束,此时梁中性轴的曲率降为λ2κ1。设新的卸载相边界的高度分别为yb1和yb2,卸载相边界U1处由于卸载应变减小了δ,相边界U2处的应变为λ2Hκ1。因此卸载相边界U1和U2的高度分别为:

(18)

截面上的应力分布表达式为:

(19)

继续进行卸载,截面上应力的分布、相边界的移动规律等均与表层材料为混合相时的卸载规律相同。

3.3弯矩曲率关系

根据以上各个阶段的应力分布,将应力的表达式代入 (8) 式可得不同卸载阶段的弯矩曲率关系。

当κ2<κi<κ4时,即加载至表层材料为混合相时，卸载的弯矩表达式为:

(20)

当κi>κ4时,即加载至表层材料为马氏体相时卸载的弯矩表达式为:

(21)

4　结果分析

加卸载阶段的无量纲弯矩曲率关系如图6所示。

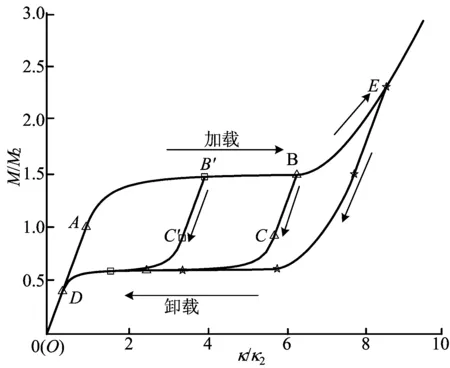
图6　弯矩-曲率关系

由图6可知，两阶段均表现出明显的非线性伪弹性滞回特性,图6中的M2=EIκ2,即表层材料开始发生相变时对应的弯矩,图6和图1中的字母一一对应。弹性加载段(OA)的弯矩和曲率呈线性关系,当表层材料发生相变后,梁的抗弯刚度降低,弯矩曲率曲线(AB)的斜率降低,曲率持续增加,而弯矩变化并不大。当表层材料相变完成后,梁的抗弯刚度进一步增大,弯矩曲率曲线(BE)的斜率再次增大。而在卸载阶段,无论加载结束时表层材料处于混合相还是马氏体相,卸载后都会发生弹性卸载,如图中的BC、B′C′等,并没有发生逆相变,该阶段的弯矩曲率关系呈线性;而在逆相变开始后,弯矩曲率关系呈现出明显的非线性,卸载的曲线和加载曲线并不重合,直至逆相变完全结束(D),再次进入弹性卸载阶段。

加载结束时表层材料为混合相和马氏体相后进行卸载的相边界演化图如图7所示。

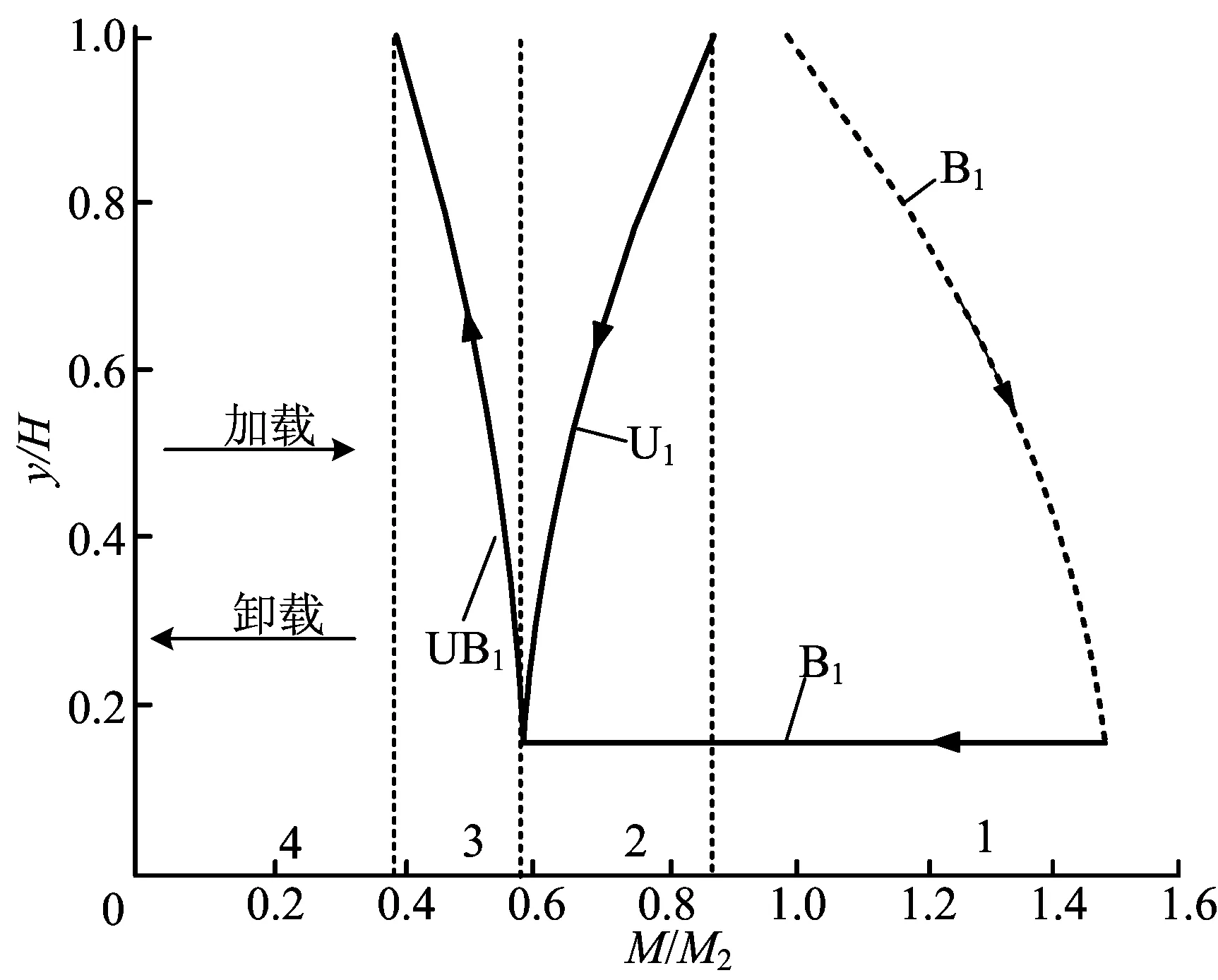
(a)　κ2<κi≤κ4

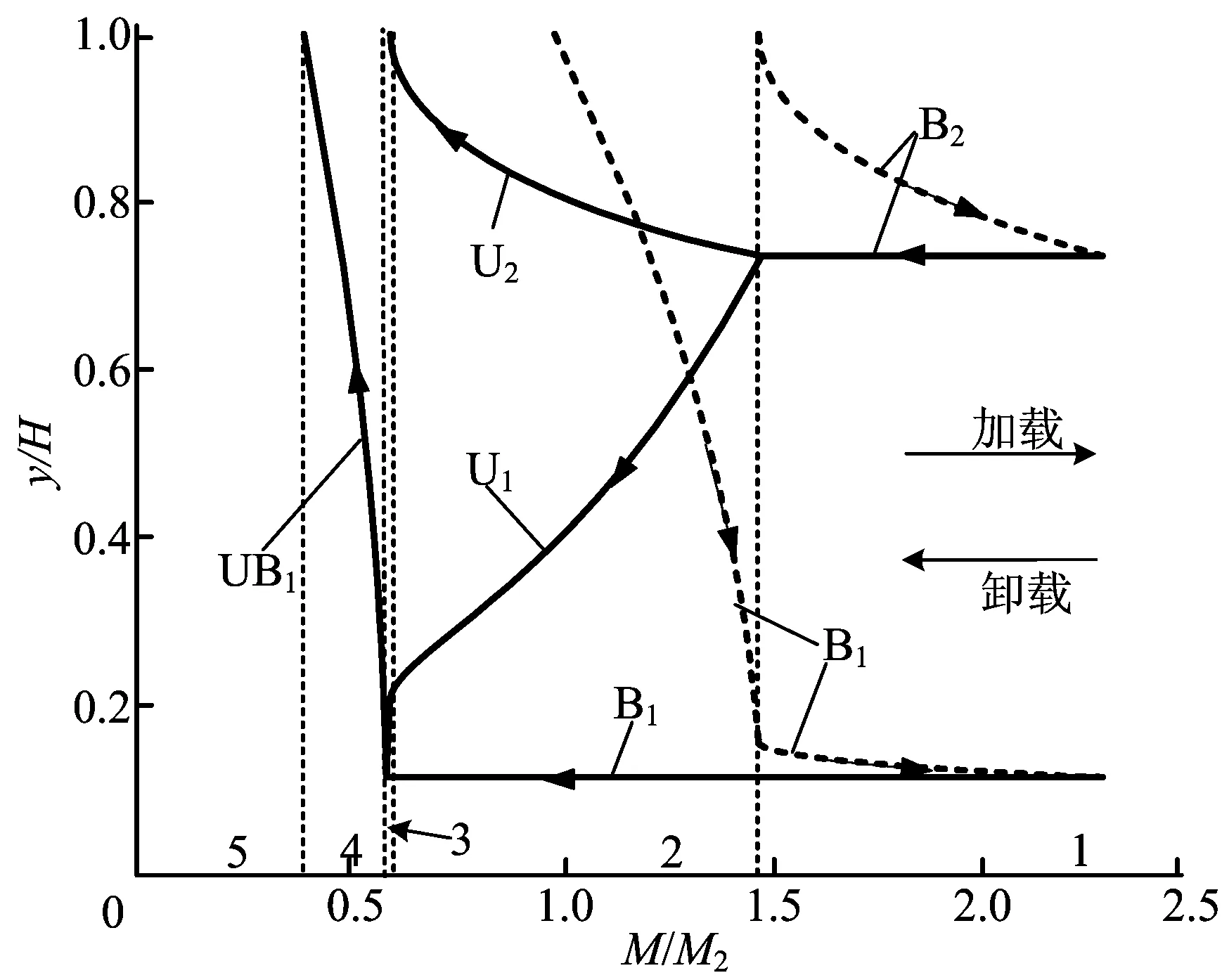
(b)　κi>κ4

图7中的数字代表卸载的阶段。加载阶段的相边界B1和B2用虚线表示,卸载阶段的相边界用黑实线表示,箭头指向代表运动的方向。在加载阶段,随弯矩的增大,表层材料率先发生相变或相变完成,相边界自表面向梁中心扩展,当表层材料为混合相时,相边界B1随弯矩增大迅速向截面中心移动,一旦表层材料相变完成,相边界B1向中心扩展的速度明显趋缓。

5　结　　论

本文基于平截面假定,对理想伪弹性SMA梁纯弯曲条件下某截面的变形行为进行了分析,揭示了梁截面上相变区的发展演化过程以及相边界的运动规律,给出了加卸载过程中应力和曲率、弯矩和曲率之间的解析表达式,得出以下结论:

(1) 梁截面上的弯矩曲率关系表现出明显非线性的滞回,呈现出材料本身特有的伪弹性特性,卸载结束后并没有残余变形。

(2) 加载阶段,截面上的应力幅值随距中性层距离的增大而单调增大,相边界随弯矩的增大向中性轴方向移动。

(3) 卸载阶段,截面上的应力沿截面高度方向不具有单调性,卸载相边界的个数、运动方向与加载结束时表层材料所处的状态有关。当加载结束时表层材料处于混合相时,逆相变首先从表层开始,形成一个向中心传播的卸载相边界,整个过程只有一条移动的相边界;而当加载结束时表层材料处于马氏体相时,逆相变首先发生在马氏体相和混合相的界面上,形成2个移动方向相异的卸载相边界。无论加载结束时表层材料处于何种状态,逆相变最终均在表层完成。

[1]唐志平.冲击相变[M].北京:科学出版社,2008:160-180.

[2]刘丽华，陈九磅，周汉义，等.形变对铜基形状记忆合金相变之后宽度的影响[J].合肥工业大学学报(自然科学版)，2002，25(2)：295-297.

[3]ATANAKOVIC T,ACHENBACH M.Moment curvature relations for a pseudoelastic beam [J].Continuum Mechanics and Thermodynanics,1989,1(1):73-80.

[4]AURICCHIO F,SACCO E.A superelastic shape-memory-alloy beam model[J].Journal of Intelligent Material Systems and Structures,1997,8(6):489-501.

[5]AURICCHIO F,SACCO E.A temperature-dependent beam for shape-memory alloys:constitutive modeling,finite-element implementation and numerical simulations [J].Computer Methods in Applied Mechanics and Engineering,1999,174(1):171-190.

[6]RANIECKI B,REJZNER J,LEXCELLENT C.Anatomization of hysteresis loops in pure bending of ideal pseudoelastic SMA beams [J].International Journal of Mechanical Sciences,2001,43(5):1339-1368.

[7]MIRZAEIFAR R,DESROCHES R,YAVARI A,et al.On superelastic bending of shape memory alloy beams [J].International Journal of Solids and Structures,2013,50(10):1664-1680.

[8]FLOR D L S,URBINA C,FERRANDO F.Asymmetrical bending model for niti shape memory alloy wires:Numerical simulations and experimental analysis [J].Strain,2011,47(3):255-267.

(责任编辑闫杏丽)

Research on bending properties for ideal pesudo-elastic shape memory alloy beam

CUI Shitang1,2，LIU Shuli2，WANG Bo1，ZHANG Ke1

(1.CAS Key Laboratory of Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230026，China; 2.No.4 Dept., Army Officer Academy, Hefei 230031, China)

Using an ideal pesudo-elastic constitutive model of shape memory alloy(SMA), the behavior of the SMA beam section under pure bending condition is analyzed. The analytical expressions of stress, moment and curvature are deduced. The moment-curvature relationships show nonlinear hysteretic characteristic. The development and evolution of phase constituents and the moving law of phase boundaries are revealed. The phase boundaries move to the neutral axis with the increase of moment during the loading stage, while during the unloading stage, the change law of phase boundaries is relate to the state of surface material and the degree of unloading and exhibits completely different properties.

shape memory alloy(SMA); pure bending; phase transformation; moment-curvature relationship

2015-04-27；

2015-07-09

安徽省自然科学基金资助项目(1408085ME84)

崔世堂(1978-),男,山东临沂人,博士,中国科学技术大学副研究员.

10.3969/j.issn.1003-5060.2016.08.008

O347

A

1003-5060(2016)08-1043-06