基于ABAQUS和MATLAB的断层抗大变形管道长度计算

王亮，房茂立中石化石油工程设计有限公司，山东东营257026

基于ABAQUS和MATLAB的断层抗大变形管道长度计算

王亮，房茂立
中石化石油工程设计有限公司，山东东营257026

通过对比抗大变形管材与普通管材力学性能和经济成本，阐述了确定活动断层处抗大变形钢管道长度的必要性。在忽略活动断层面宽度条件下，研究采用有限元软件ABAQUS对该处普通钢管道进行抗震受力计算，得到管道沿线应变。利用MATLAB软件对大于容许应变值的管道单元进行统计处理，得到大于普通钢管容许应变值的管道长度，加上活动断层面宽度之和即为需要使用抗大变形管道的长度。此方法可得到抗大变形钢管道长度及沿管道长度方向应变分布状况，为活动断层作用下管材选择提供依据。

ABAQUS；MATLAB；断层；抗大变形管；长度

由于长输管道分布范围广，沿途区域自然地理条件和地质环境复杂多样，无法完全避开地质灾害的威胁和侵害。在多种地质灾害中，活动断层是破坏埋地管道完整性的高发地。GB 50470-2008《油气输送管道线路工程抗震技术规范》、ASCE 2004 “Guidelines for the Seismic Design of Oil and Gas Pipeline Systems”及ALA 2001“Guidelines for the Design of Buried SteelPipe”均提出了穿越活动断层处管道基于应变的设计思想和技术方法，通过调整管道穿越活动断层处夹角、壁厚及埋深，使得断层处管道受力满足管道材料力学性质。然而，由于某些活动断层位错量大、断层性质复杂，使用以上设计方法进行管道受力校核无法满足其力学特性。因此，在这些活动断层处需要使用抗大变形管，这类管材除了拥有优于普通钢管的材料性能（屈服强度明显低于普通管材，而应变强化指数明显高于普通管材，均匀延伸率大于8％，屈曲应变是普通管材的1.5倍），还具备高应力比、抵抗纵向屈曲的高变形容量等特性［1］。但抗大变形钢管的成本比普通钢管高25％左右，为控制工程成本，有必要严格核算抗大变形钢管用量。

1 活动断层处抗大变形管长度计算

根据GB 50470-2008提供的活动断层处管道抗震受力计算方法，在忽略断层面宽度的条件下，采用有限元软件ABAQUS对该处普通钢管进行抗震受力计算，得到所有结点的应变值。利用MATLAB软件处理、分析计算结果，把大于容许应变值的结点进行统计处理，得到大于普通钢管容许应变值的管道长度，加上活动断层面宽度之和即为需要使用抗大变形管的长度。

2 基于ABAQUS的活动断层处普通钢管抗震计算

2.1基础理论

2.1.1管-土作用

当管-土作用产生较大位移或变形时，管道和土体的变形会进入非线性状态，此时理论分析方法变得非常复杂且困难。随着计算机技术的发展，多种基于有限元模型的分析方法被用于描述管-土间的相互作用［2］。土弹簧模型就是一种用于分析地下结构与土体相互作用关系的简化模型，它将管道周围土体简化为一系列的等效弹簧，弹簧的刚度和自由度则由土质和土体运动形式决定［3］。

在断层的错动作用下，管道和周围场地土之间存在相互作用［2］。一般采用三个方向的土弹簧进行模拟：如图1所示［4］。

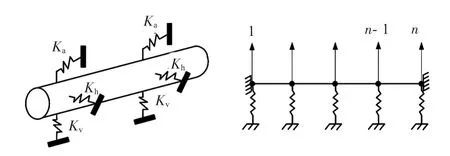
图1　土弹簧模型示意

管轴方向的土弹簧Ka描述的是沿管轴方向土对管道的摩擦阻力，其参数主要由管沟内的回填土决定。水平横向土弹簧Kh和垂直方向土弹簧Kv描述的是管道在管轴横向受到的周围土压。垂直方向土弹簧又可分为垂直向上土弹簧和垂直向下土弹簧，其参数主要由断层附近的场地土决定。

假设管道周围土体状态均匀一致，当管-土间相对位移达到最大值（屈服位移）后，管-土间相互作用力为恒定值，以此确定土弹簧刚度，如图2所示［4］。

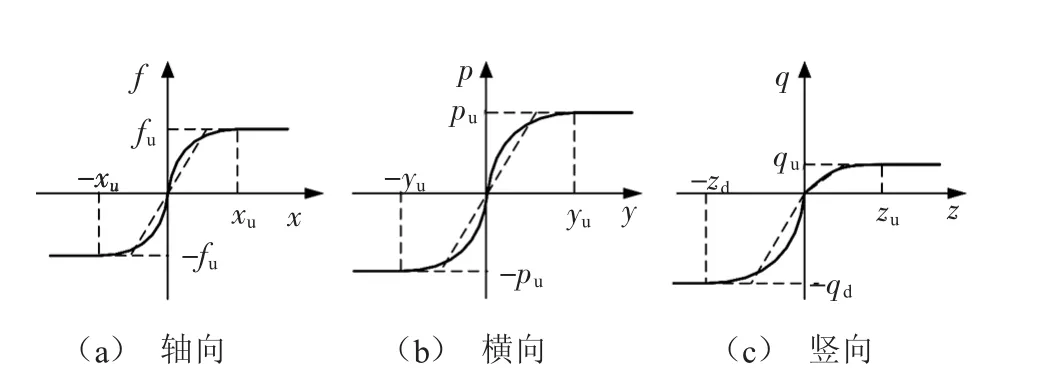
图2　土弹簧模型

2.1.2管-土模型

管道应变有限元计算中，管道一般用梁、管或壳单元离散，其中采用管单元计算时间短且计算精度能满足工程需要。由于直管单元没有考虑管道的椭圆化变形，且在断层位移作用下管-土之间存在较大相对位移的范围为断层两侧十几米到三十米［5］，因此可将离断层较远（左右各1 000 m）的管道采用管单元PIPE31离散，管道单元的长度取1 m；在断层附近（左右各100 m）采用弯管单元ELBOW31，管道单元的长度取0.1 m，两端采用固定边界条件。管-土单元划分模型见图3。使用PSI单元来模拟埋地管道与土体间的相互作用。

根据以上管-土模型建立方法，以某正断层处普通钢管（材质X80）为实例进行有限元分析计算，管道及断层参数分别见表1和表2。

图3　管-土单元划分模型/m

表1　管道参数

表2　正断层参数

2.2计算程序思路

基于上述原理和建模思想，设计图4所示的计算程序。

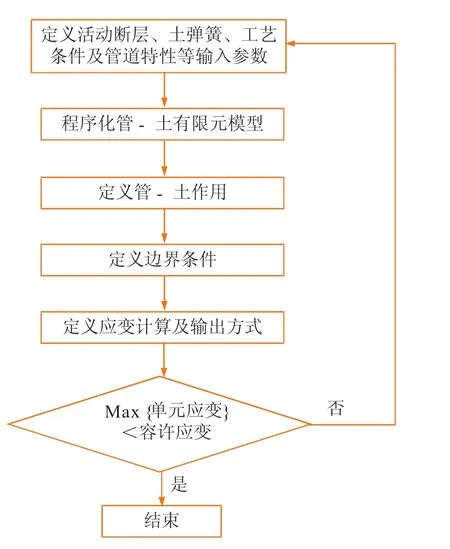
图4　活动断层作用下管道有限元计算思路

2.3计算结果分析

对该正断层作用下管道有限元模型，在满足规范对活动断层处管道设计要求的条件下，经过不断的调整管道与活动断层夹角、埋深、壁厚等参数，得到单元最小应变值1.735 4％，比管道最大容许拉伸应变值高15.69％。因此，在该活动断层条件下，并不适用普通钢管，需要使用抗大变形钢管。

在该实例模型中，建立了2 000个单元，每个单元中有40个积分点，在每个单元的40个应变值中，有些是重复相等的数值。因此，如何使用这些应变值计算抗大变形管长度有一定的技术困难。经过分析对比各种编程软件，本文采用易于处理大量数据矩阵的MATLAB软件进行编程，从80 000个数值中提取有效数据，计算需要使用的抗大变形管长度。

3 基于MAL TAB的活动断层处使用抗大变形钢管长度计算

3.1基础原理

当钢管应变大于0.5％时，继续施加载荷，管材将会进入弹塑性区，长期在该区间运行，将会影响管道使用寿命，甚至极易断裂破坏［6］。因此，在利用MATLAB读写文件数据函数把有限元计算结果写入工作空间后，应首先筛选出应变值大于0.5％的单元及对应的应变数值，在此数值范围基础上计算抗大变形管长度。对于同一单元重复的应变数值，使用频率统计函数将这些数据进行唯一化处理，形成每个单元对应最大应变值的矩阵。

3.2计算程序思路

基于活动断层作用下普通钢管有限元计算结果和MATLAB函数程序设计的计算程序如图5所示。

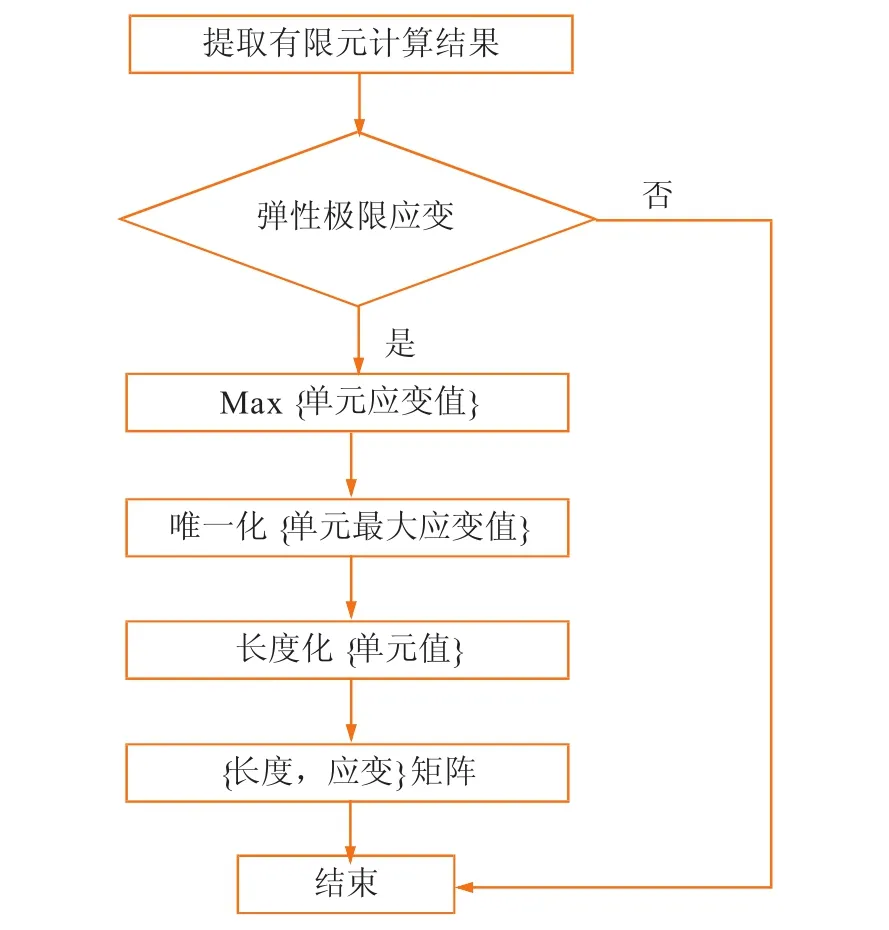
图5　活动断层作用下抗大变形管长度计算程序框架

首先，提取计算结果；其次，将计算结果逐一与普通管材弹性极限应变相比，若小于，则结束程序，若大于，则求取每一单元最大应变值；然后，去除每一单元重复应变值，确保单元与应变值一一对应；最后，将相应单元值转换为管道长度，形成长度、应变矩阵。运行程序即可生成抗大变形管长度与应变关系曲线图，从图中可得到所需抗大变形管长度、沿管道长度方向的应变分布、活动断层处应变值、管道最大应变值及位置等信息。

3.3计算结果分析

采用上述程序设计思路对该实例正断层作用下普通钢管有限元计算结果进行分析计算，得到忽略断裂带宽度条件下所需使用的抗大变形钢管长度、沿管道长度方向应变分布状况、断层面位置处钢管应变值、钢管最大应变值及产生最大应变值位置等关键数据，如图6所示。

从图6可以看出，该穿越段管道最大应变值为1.7354％，断层面位置处钢管应变值为0.973 2％，大于容许应变值的管道长度约36 m。从图中远离断层面和断层面中心附近两区域分析抗大变形钢管应变变化情况，可见远离断层面的管道应变分布关于应变坐标轴近似对称，越靠近断层面应变值越大，离断层面越远应变值越小；断层面中心附近的管道应变呈“高峰低谷”分布。综合考虑计算结果与断裂带宽度，该正断层处穿越段管道最大应变位置距管道起始穿越点长度约116 m，所需使用的抗大变形钢管长度约236 m。

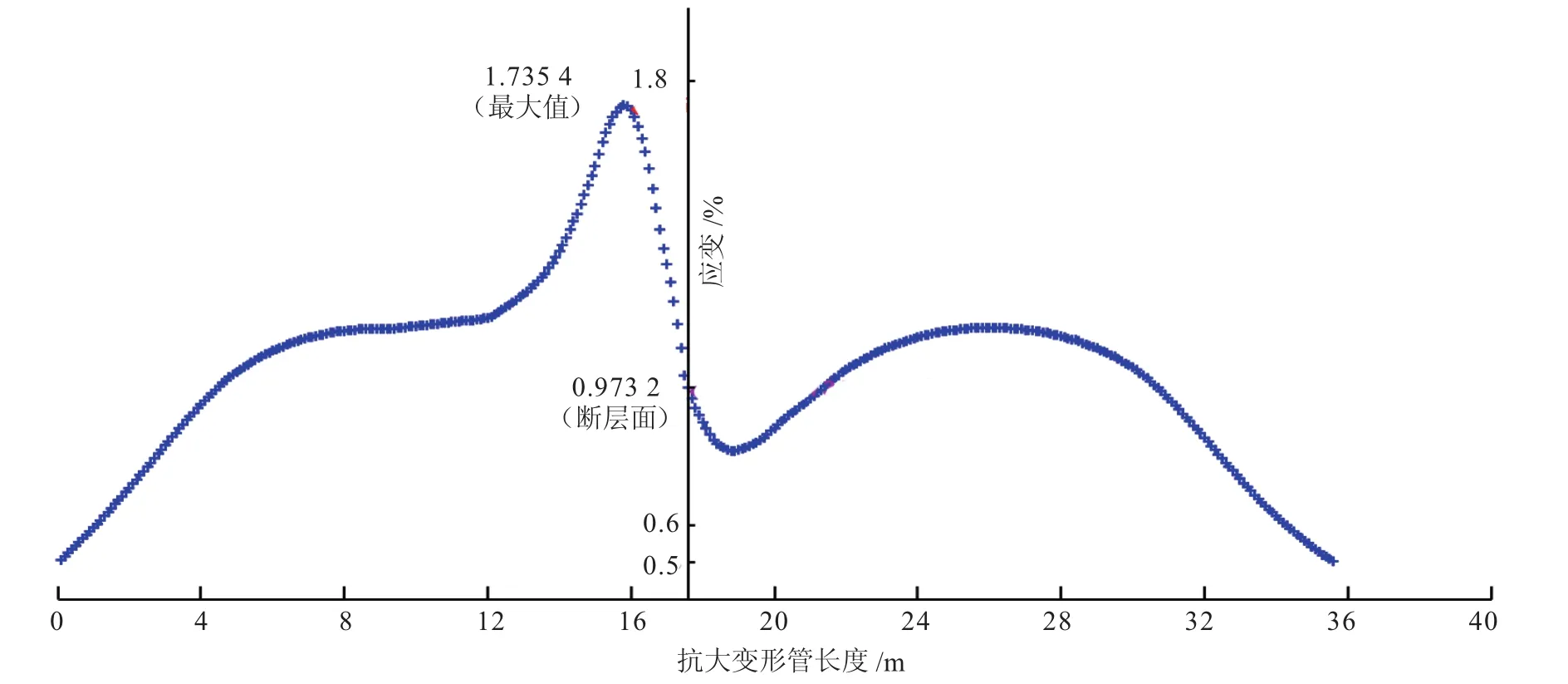
图6　某正断层作用下抗大变形钢管长度与应变分布关系曲线

4 结束语

抗大变形钢管长度、沿管道长度方向应变分布状况、断层面位置处钢管应变值、钢管最大应变值及产生最大应变值位置等信息，是穿越断层处管材选择的重要依据。以往类似工程经常通过Newmark-Hall解析法或经验法选择管材，易造成管材性能“不足”或“过盈”的局限性。本文在对比抗大变形管材与普通管材力学性能、经济成本的基础上，围绕如何确定活动断层作用条件下抗大变形钢管长度，在忽略活动断层面宽度条件下采用ABAQUS和MATLAB计算抗大变形钢管长度、沿管道长度方向应变分布状况、断层面位置处钢管应变值、钢管最大应变值及产生最大应变值位置等信息，为断层处管材选择提供了依据。

［1］王伟，严伟，胡平，等.抗大变形管线钢的研究进展［J］.钢铁研究学报，2011，23（2）：1-6.

［2］闫相祯，张立松，杨秀娟.管道穿越地震断层管土耦合大变形壳模型的应变响应规律研究［J］.土木工程学报，2010，43（8）：132-139.

［3］ASCE 2004，Guidelines for the Seismic Design of Oil and Gas Pipeline Systems［S］.

［4］GB 50470-2008，油气输送管道线路工程抗震技术规范［S］.

［5］KENNEDY R P，CHOW A W，WILLIAM R A.Fault movement effects on buried oil pipeline［J］.Journal of Transportation Engineering，1977，103（5）：617-633.

［6］刘鸿文.材料力学［M］.北京：高等教育出版社，2009.

Using ABAQUS and MATL ABto Calculate L ength of High Deformability Steel Pipeline Crossing Active Fault

WANG Liang，FANG Maoli
Sinopec Petroleum Engineering Corporation，Dongying 257026，China

This paper introduces the necessity of calculating the length of high deformability steel pipeline crossing active fault by comparing mechanical properties and economic costs between the high deformability steel pipeline and the common steel pipeline.Under the condition of ignoring activity fault plane width，the seismic resistance of the common steel pipeline is calculated by the finite element software ABAQUS，and the strains along the pipeline are obtained.Then，the pipe elements which have the strains greater than the allowable strain value are identified and dealt with by software MATLAB，and the corresponding pipeline length is obtained.The corresponding pipeline length plus the activity fault plane width is the totalnecessary length of pipeline having the strains greater than the allowable strain value.This method can obtain the necessary pipeline length and strain distribution along the pipeline length，also provide the basis of choosing pipes for crossing the active fault.

ABAQUS；MATLAB；fault；high deformability pipe；length

10.3969/j.issn.1001-2206.2016.04.008

王亮（1987-），男，山东武城人，助理工程师，2014年毕业于中国石油大学（华东）石油与天然气工程专业，硕士，现从事油气长输管道强度设计与分析方面工作。

Email：281814156@qq.com

2015-12-23；

2016-04-23