一种降低MIMO-OFDM系统PAPR的低复杂度SLM算法

李 玮，刘雲雲，杨 霖

（1.四川邮电职业技术学院实验实训中心，成都 610067； 2.电子科技大学通信抗干扰技术国家级重点实验室，成都 611731）

一种降低MIMO-OFDM系统PAPR的低复杂度SLM算法

李 玮1，刘雲雲2，杨 霖2

（1.四川邮电职业技术学院实验实训中心，成都 610067； 2.电子科技大学通信抗干扰技术国家级重点实验室，成都 611731）

为了降低MIMO-OFDM（多输入多输出正交频分复用）系统中传统SLM（选择性映射）算法的计算复杂度，文章提出将原始频域信号分成实部和虚部后分别进行不同的相位旋转，再通过IFFT（快速傅里叶逆变换）调制模块得到相应的时域序列，最后通过多天线间实部和虚部序列的不同组合来产生更多的具有不同PAPR（峰均功率比）的备选序列。仿真结果表明，所提算法能有效地抑制MIMO-OFDM信号的PAPR。相比传统SLM算法能有效降低计算复杂度。

多输入多输出正交频分复用；选择性映射；峰均功率比；计算复杂度

0　引 言

MIMO（多输入多输出）技术在不需要增加频谱资源和天线发送功率的情况下，可以成倍地提高信道容量［1］。OFDM（正交频分复用）信号由于具有较高的PAPR（峰均功率比），在通过非线性器件时，常导致通信质量下降［2］。而MIMO-OFDM信号随着天线数的增加，PAPR问题会越来越严重。为了降低MIMO-OFDM信号的PAPR，国内外学者提出了很多方法，大致可以分为两类：信号预畸变和信号非畸变。信号预畸变是在信号被送到功率放大器之前对高峰值信号进行非线性处理，使其不超出放大器的动态范围，而抑制PAPR会引入多余的非线性失真，从而导致传输性能下降，其代表方法为限幅法［3］。对于信号非畸变方法，目前研究最多且最有效的算法是PTS（部分传输序列）［4-5］算法。

综合国内外研究情况可以看出，目前一些降低MIMO-OFDM信号PAPR的方法大多是在频域利用IFFT（快速傅里叶逆变换）的性质，通过信号处理的方法来减少IFFT次数，同时利用子块之间的位置交换来获得更多的序列，而且很少有考虑到同时降低边带信息。

本文提出的M-SLM（改进的选择性映射）算法是将原始频域信号通过实部和虚部划分后分别乘以不同的相位旋转序列，经IFFT调制模块得到相应的时域信号序列，最后通过天线间信号的实部和虚部序列的不同组合来产生更多的具有不同PAPR的备选序列。与传统SLM算法相比，所提算法在不增加IFFT次数的情况下，利用不同天线这一维度来产生更多的备选序列仅仅需要少量的复数加法运算，从而降低了系统的计算复杂度。

1　M-SLM算法的基本思想

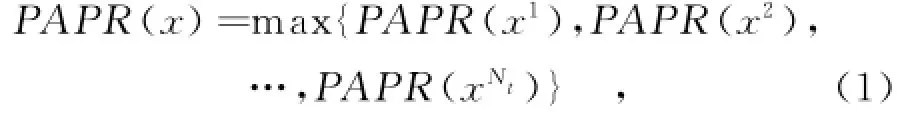
式中，PAPR（xi）为每根天线PAPR的最小值。

为了降低传统SLM算法的复杂度，文献［6］提出了一种WL-SLM（广义线性SLM）算法，其基本思想是将原始频域信号划分成实部和虚部，再分别乘以不同的相位旋转因子得到不同的序列，每种序列分别通过IFFT调制模块得到相应的时域序列，将不同的实部和虚部序列进行组合得到更多具有不同PAPR的备选序列，最后选出一个PAPR最小的序列传输。但该方法仅能在单天线OFDM系统中使用。

本文在WL-SLM算法的基础上，将该算法从OFDM系统扩展到了MIMO-OFDM系统，提出了一种基于天线间信号交换的M-SLM算法。利用MIMO系统的多天线这一维度，将天线间信号的实部和虚部进行不同组合，当使用相同的IFFT次数时，M-SLM算法可以产生比传统SLM算法和每根天线单独使用WL-SLM算法更多的备选序列。因此，在产生相同数量的备选序列情况下，M-SLM算法能有效地降低计算复杂度。

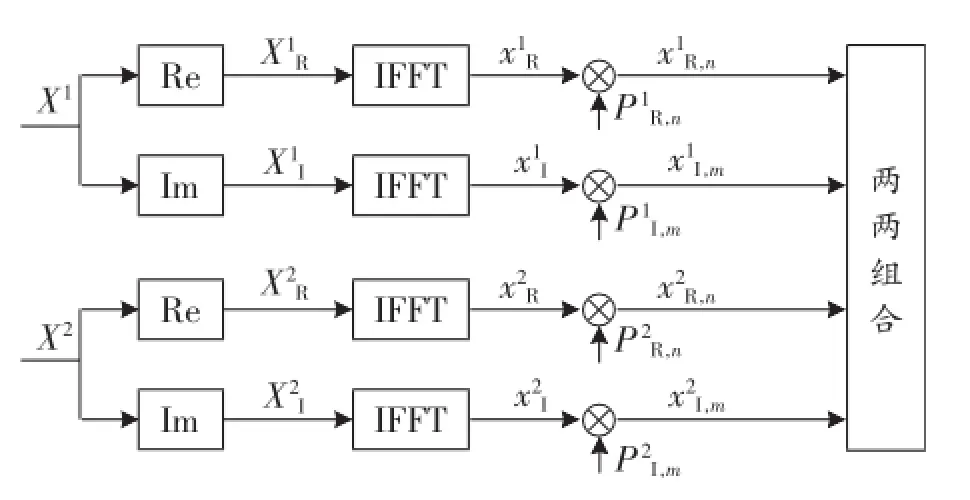
图1 M-SLM算法发送端框图

图1所示为M-SLM算法发送端框图。以两根发射天线为例，第i根天线上复信号为Xi=［Xi（0）对其进行实部和虚部的划分，得到，其中和分别为实数序列实部和虚部。采用不同的相位旋转因子序列和， M为相位因子数。原始信号分别与相位因子相乘，得到不同的频域序列：

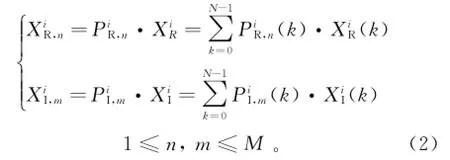
图2所示为M-SLM算法备选序列选择情况。

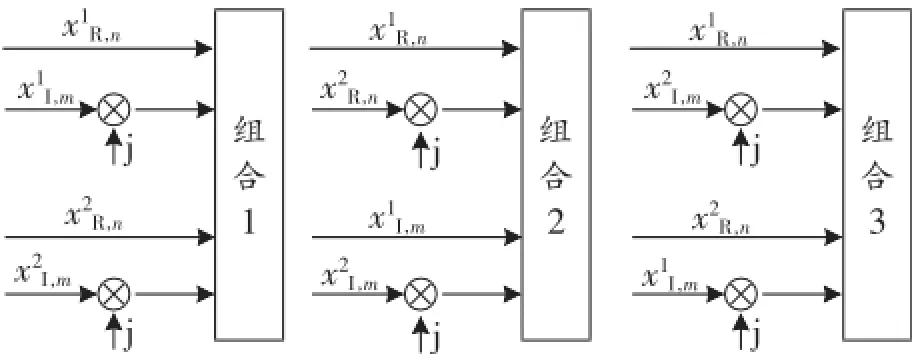
图2　M-SLM算法备选序列选择情况

组合1～3与OFDM系统的WL-SLM算法一样，将每根天线不同时域的实部和虚部序列分别组合，并利用天线2中信号的实部和虚部分别与天线1中的虚部进行位置交换，可以得到不同的备选序列：

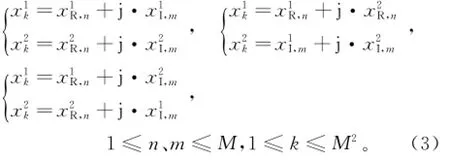
由于每根天线的实部和虚部分别乘以相位因子后通过IFFT调制得到了M组时域序列，通过式（3），每根天线共可以得到3M2种不同的备选序列，从PAPR最小的备选序列组中选出PAPR最小的序列传输。

综上所述，M-SLM算法的基本步骤如下：

（1）将每根天线的原始频域信号序列划分为实部和虚部序列，分别命名为和

（2）每根天线的实部和虚部序列分别乘以M种不同的相位因子得到不同的序列，然后再分别进行IFFT调制得到时域信号和。

（3）将每根天线的实部和虚部序列进行不同组合，总共可以得到M2种不同的备选序列。

（5）分别计算每组的M2种备选序列的PAPR，然后得到系统的PAPR。

以上为两根发射天线的MIMO-OFDM系统发射端信号的PAPR抑制处理，对于更多发射天线的系统，可以将发射天线两两分组并运用两根天线的M-SLM方法，通过减小每个天线对的PAPR来降低整个系统的PAPR。虽然这种拓展是通过每个天线对的PAPR达到最小来使整个天线的PAPR得到抑制，而不是所有天线联合起来考虑，但M-SLM算法充分利用了两根天线的实部和虚部的不同组合来产生更多的备选序列，因此每个天线对的PAPR能得到很好的抑制，从而整个系统的PAPR也能得到很好的抑制。

本文是将原始频域信号划分为实部和虚部序列分别进行IFFT，传统SLM算法是复信号进行IFFT，而对复信号直接进行IFFT和将其划分为实部与虚部后再分别进行IFFT运算的计算量相同。

对于每根天线，当子载波数为N、过采样率为L、备选序列数为K=3M2时，传统SLM算法需要3M2次N点的复数乘法实现相位因子与原始序列相乘，3M2次LN点的IFFT运算得到时域备选信号；而M-SLM算法只需要2M次N点实数乘法实现相位因子与序列相乘，这相当于M次N点的复数乘法运算，M次实部信号和M次虚部信号LN点的IFFT运算得到时域信号，相当于M次LN点的复数IFFT运算，然后通过实部和虚部的不同组合，需要3M2次LN点复数加法实现不同实部和虚部的叠加来产生3M2种不同的备选序列。

由文献［4］可知，当OFDM信号的子载波数为N、过采样率为L时，一次IFFT运算需要（LN· log2N/2+LN/2）次复数乘法运算和（LN·log2N）次复数加法运算。表1所示为备选序列数为3M2时，传统SLM算法与M-SLM算法的复杂度比较。

表1　几种算法的复杂度比较

由表1可知，当备选序列个数都为3M2时，M-SLM算法需要的复数乘法次数为传统SLM算法的1/（3M），复数加法次数为（1/log2N+1/（3M）），随着备选序列的增加，这一比值变小。因此MSLM算法极大地降低了传统SLM算法的计算复杂度。

2　仿真结果与分析

本文给出了调制方式为QPSK（四相相移键控）、发射天线数Nt=2、子载波数N=256、过采样率L=4、仿真次数为105时，传统SLM算法、多天线WL-SLM算法［6］和M-SLM算法在相同IFFT次数时的PAPR性能、相同备选序列数时的PAPR性能以及计算复杂度性能曲线。

图3给出了不同算法在IFFT次数相同（M= 3）情况下的PAPR性能曲线。图中，PAPR0表示PAPR门限；Pr［PAPR＞PAPR0］表示PAPR＞PAPR0的概率。由图可知，有1%的数据帧超过某一PAPR时，传统SLM算法、WL-SLM算法和MSLM算法的PAPR分别为9.3、8.5和8 dB。在相同IFFT次数的情况下，M-SLM具有更好的PAPR抑制性能。此时，传统SLM算法、WL-SLM算法和M-SLM算法的备选序列数分别为3、9和27。由此可见，在相同次数的IFFT运算条件下，M-SLM算法能产生更多的备选序列且仅需要少量额外的复数加法运算，具有很好的PAPR抑制性能。

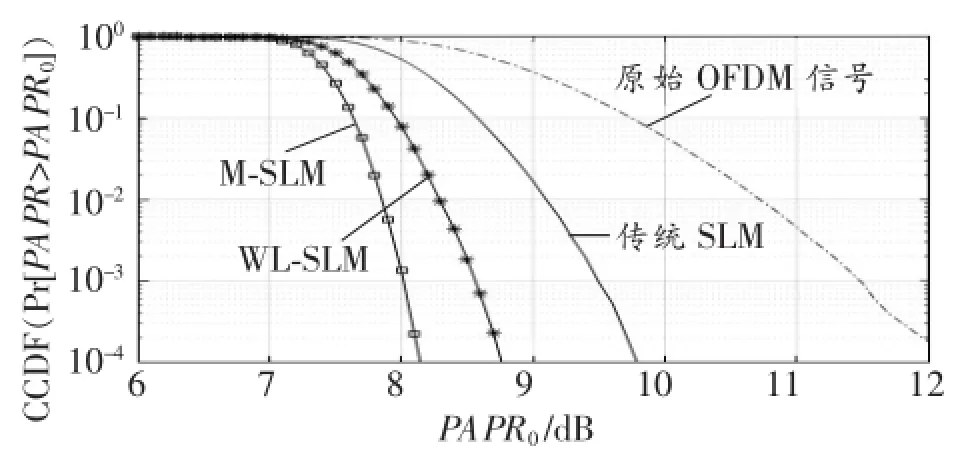
图3 不同算法在相同IFFT次数时的PAPR曲线

图4为相同备选序列数时，传统SLM算法和M-SLM算法的PAPR性能曲线。当备选序列个数K=27，有1%的数据帧超过某一PAPR时，传统SLM算法和M-SLM算法的PAPR分别下降到7.85和8 dB，两者相差0.15 dB，意思是传统SLM算法中仅有1%的传输信号PAPR值大于7.85 dB。这是因为M-SLM算法的备选序列分成了3组，先计算每组备选序列的最小PAPR，然后在3个组中选择最小PAPR作为系统的PAPR，而传统SLM算法所有备选序列都是独立的，每根天线从所有的备选序列中选择一个最小的PAPR，因此每根天线在选取最小PAPR时具有更大的选择自由度，因此传统SLM算法的性能比M-SLM算法稍好。但MSLM算法具有更低的计算复杂度，图5所示为两种算法的计算复杂度性能曲线。

图4　几种算法在相同备选序列数时的PAPR曲线

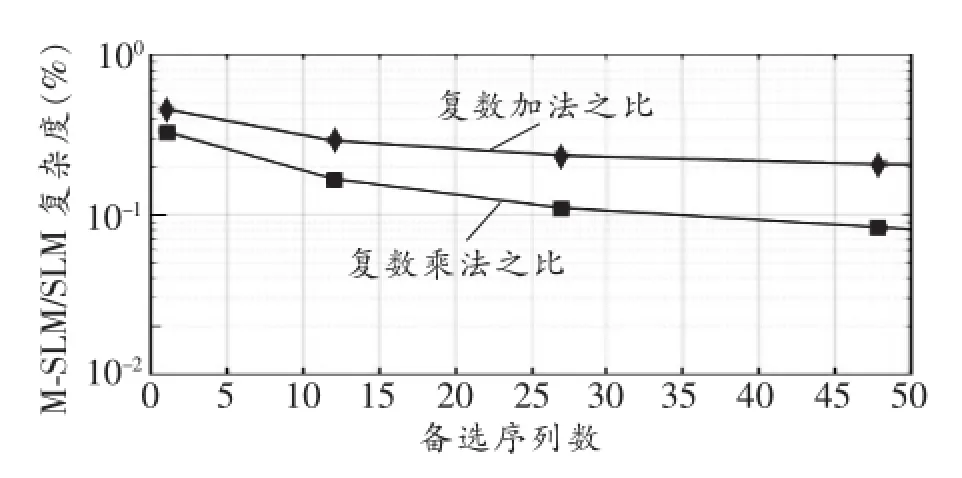
图5　计算复杂度性能曲线

根据表1中本文提出的M-SLM算法和传统SLM算法在不同备选序列数下的公式，绘制了图5所示的计算复杂度性能曲线。由图5和表1可知，当备选序列数K=3M=27时（对应M=3），M-SLM算法的复数乘法和复数加法次数分别为传统SLM算法的1/（3M）=11.1%和1/log2N+1/（3M）= 1/log2256+1/（3×3）=23.6%，随着备选序列的增加，这一比值将进一步减小。因此，本文所提的MSLM算法能有效地降低系统的计算复杂度。

3　结束语

本文提出了一种M-SLM算法，将原始频域信号通过实部和虚部划分后分别进行不同的相位旋转，再通过IFFT调制模块得到时域信号，最后利用MIMO系统中多天线这一维度，将天线间信号的实部和虚部进行不同的组合，得到更多具有不同PAPR的备选序列。仿真结果表明，在产生相同备选序列数的情况下，M-SLM算法能有效地降低系统的计算复杂度，且能得到与传统SLM算法相似的PAPR的抑制性能。

［1］ Chockalingam A.Large MIMO Systems［M］.Cambs：Cambridge University Press，2014.

［2］ Costa E，Midrio M，Pupolin S.Impact of amplifier nonlinearities on OFDM transmission system performance［J］.IEEE Communication Letters，1999，3（2）：37-39.

［3］ Jiang Yang，Yuan Min，Chen Bi-yun.Modified united algorithm for reducing PAPR of MIMO-OFDM system［J］.Application Research of Computers，2012，29（1）：251-257.

［4］ 胡武君.联合空、时、频域处理算法降低MIMOOFDM系统的PAPR［D］.成都：电子科技大学，2015.

［5］ Ku S J.Low-Complexity PTS-Based Schemes for PAPR Reduction in SFBC MIMO-OFDM Systems［J］. IEEE Transactions on Broadcasting，2014，60（4）：650-658.

［6］ Yang L，Hu W J，Soo K K.Swapped SLM scheme for reducing the PAPR of OFDM systems［J］.IET E-lectronics Letters，2014，50（22）：1608-1609.

A Low Complexity SLM Algorithm for Reducing PAPR of MIMO-OFDM System

LI Wei1，LIU Yun-yun2，YANG Lin2
（1.Experimental Training Center，Sichuan Vocational College of Post and Telecom，Chengdu 610067，China；2.National Key Laboratory of Science and Technology on Communications，University of Electronic Science and Technology of China，Chengdu 611731，China）

In this paper，we propose a new method to reduce the computational complexity of the conventional Selective Mapping（SLM）algorithm in the Multiple Input Multiple Output Orthogonal Frequency Division Multiplexing（MIMO-OFDM）system.The original frequency domain signals are first divided into real and imaginary parts.Then the two parts are operated by different phase rotation respectively.The corresponding time domain signals are finally obtained by using inverse fast Fourier transform operations.It can produce more candidates with different Peak to Average Power Ratio（PAPR）by different combination of real and imaginary parts in antennas.The simulation results show that the proposed method can reduce the PAPR of MIMO-OFDM signals effectively.In addition，compared with conventional SLM algorithm，the proposed method can reduce the algorithm computation complexity significantly.

MIMO-OFDM；SLM；PAPR；computational complexity

TN919.3

A

1005-8788（2016）04-0056-04

10.13756/j.gtxyj.2016.04.017

2016-03-07

国家自然科学基金资助项目（61370012）

李玮（1981-），女，四川宜宾人。讲师，硕士，主要研究方向为移动通信新技术和通信与测控技术。

杨霖，副教授。E-mail：eelyang@uestc.edu.cn