基于混合Copula函数的含风电场电力系统可靠性评估

高小童，秦志龙

（1.山东省胶东调水工程棘洪滩水库管理处，山东　青岛　266001；2.国网山东省电力公司青岛供电公司，山东　青岛　266002）

基于混合Copula函数的含风电场电力系统可靠性评估

高小童1，秦志龙2

（1.山东省胶东调水工程棘洪滩水库管理处，山东青岛266001；2.国网山东省电力公司青岛供电公司，山东青岛266002）

随着风力发电的发展，风电场风速之间的相关性对电力系统可靠性的影响越来越大。基于混合Copula函数建立一种多元相关性风速的模型，并在含多个风电场的IEEE-RTS系统可靠性评估中应用该模型，通过实例分析，在描述风电场风速相关结构方面，提出的混合Copula函数法比单一Copula函数法更合适，更有优势。

风速相关性；混合Copula函数；电力系统可靠性；蒙特卡洛仿真

0　引言

风能是一种清洁的可再生能源，大力开发风电能源是合理调整电源结构的需要，也是国内能源发展战略的重要组成部分［1］。文献［1-4］在研究含风电场风速模型过程中仅仅考虑了风速随机性，没有计及风电场风速之间相关性。随着风电场的密集建设，距离较近风电场之间的风速相关性研究是确保含多个风电场电力系统可靠性的基础［5-11］。文献［5-8］提出了一种产生线性相关性风速的方法，但是该方法不能模拟风速之间的非线性相关性；文献 ［9-11］均仅将单一Copula函数理论运用到含风电场的电力系统可靠性评估中。与计及风速相关性比较，不计风速相关性会造成对含风电场发电系统可靠性乐观估计［8，11］；与混合Copula函数法相比，单一Copula函数将高估风速相关性对电力系统可靠性的影响。

提出混合Copula函数理论来模拟风电场风速相关性结构，并应用于含风电场发电系统可靠性评估。

1　基于混合Copula函数的风速相关性模型

1.1单一Copula函数

阿基米德Copula函数具有构造简单、对称性和可结合性良好等特性［11-13］。

常用的阿基米德Copula函数有Clayton Copula，Gumbel Copula和Frank Copula函数［11-13］，表达式分别为

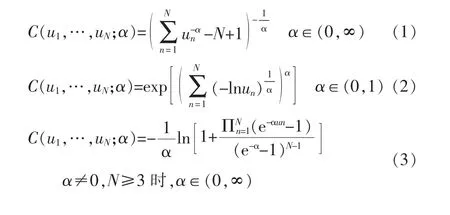
式中：α为相关参数；（u1，…，uN）为N元随机变量。

Clayton Copula、Gumbel Copula密度函数具有非对称性的相关结构，无法表达变量间对称的相关关系；Frank Copula函数具有对称性的相关结构，无法表达变量间非对称的相关关系。Clayton Copula函数适用于描述分布下尾部的变化，但Gumbel Copula并不适用；Clayton Copula函数不适用于描述分布上尾部的变化，而Gumbel Copula适用；Frank Copula对描述分布上、下尾相关性的变化均不适用［13］。

Clayton Copula、Gumbel Copula和Frank Copula函数，在描述风电场风速间相关结构方面各有不同特点［13］，某个单一Copula函数很难表达风电场风速多样性、差异性的特点。

1.2混合Copula函数

在实际应用中应采用混合Copula函数来表达风电场的相关风速数据，混合后的Copula函数为［14］

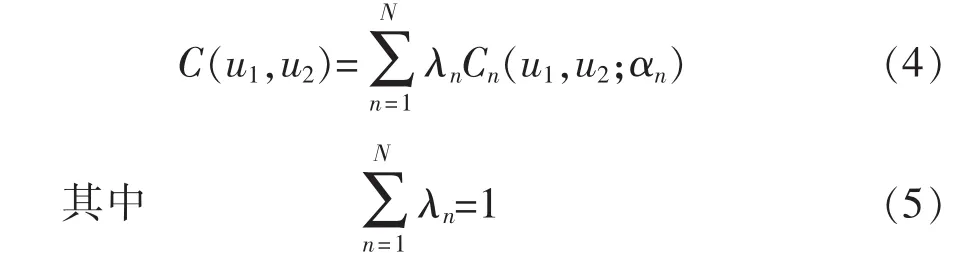
式中：Cn（u1，u2；αn）为单一 Copula函数；λn为权重系数，满足 0≤λn≤1；αn为相关参数［14］。不同的Copula函数组合，在描述风电场风速结构时的效果也有所不同。欧式距离检验法、P-P图检验法、K-S检验法是检验Copula函数拟合效果的几种常用方法［15］。

选用 Gumbel、Frank、Clayton 3种 Copula函数的线性组合构造反映风电场风速相关性的混合Copula函数［13-15］，能够反映风电场风速变化的各种情况。

2　相关风速产生方法

2.1单一Copula函数模型中的分步参数估计

利用分步参数估计法估计边缘分布函数和Copula函数中的未知参数［8，11］。

首先要确定风速的边缘分布，采用非参数核密度分布模型来表达风速边缘分布［16］。非参数核密度分布密度函数为

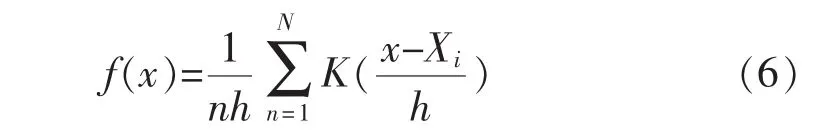
非参数核密度分布累积函数为

式中：n为样本数；Xi为样本值；h为带宽；K （·）为核函数；Φ（·）为单变量标准正态累积分布函数。

得出边缘分布的参数后，用拟牛顿法得到相关性参数α的估计值［8，11］。

式中：c为单一Copula密度函数；n为样本数；Xi为样本值；h为带宽；N为Copula函数的元数。

2.2混合Copula函数权重系数

混合Copula函数权重系数通过理论Copula函数和经验Copula函数之间的最短欧式距离来选取。经验Copula函数为［8，11-12］

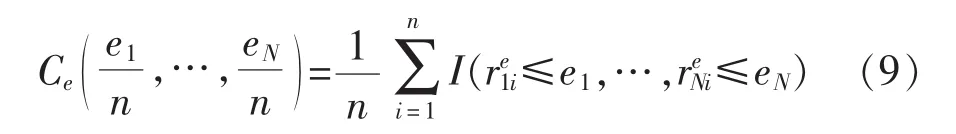
理论Copula函数与经验Copula函数之间的最短欧式距离为［8，11-12］

用欧式距离最小的理论求解选取混合Copula函数权重系数λn。

2.3多维风电场相关风速

描述风速相关结构的最优混合Copula函数确定后，采用一种合成法产生具有相关性的多维风速样本，步骤为：

1）产生U（0，1）中的一个随机数t。

2）确定i∈｛1，2，…N｝使得

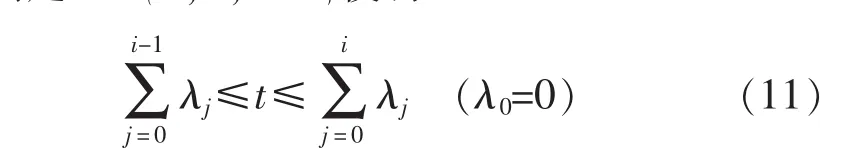
3）产生Ci（u1，u2）的一个随机数对（u1，u2）。

4）重复上述3步T次，得出服从C（u1，u2）的T个随机数对。

3　算例研究

选用的风速数据为山东青岛地区两风电场风速历史数据。

3.1选取最优混合Copula函数［8，11］

采用分步参数估计法得到单一Copula函数的参数，如表1所示。

表1　单一Copula函数参数估计值

结合表1中Copula函数的参数α，由公式（10）可以求解出混合Copula函数的权重系数λ1=0.05，λ2=0.17，λ3=0.78。

选取K-S检验法、欧式距离检验法对多个风电场相关风速的拟合效果进行检验［15］，如表2所示。

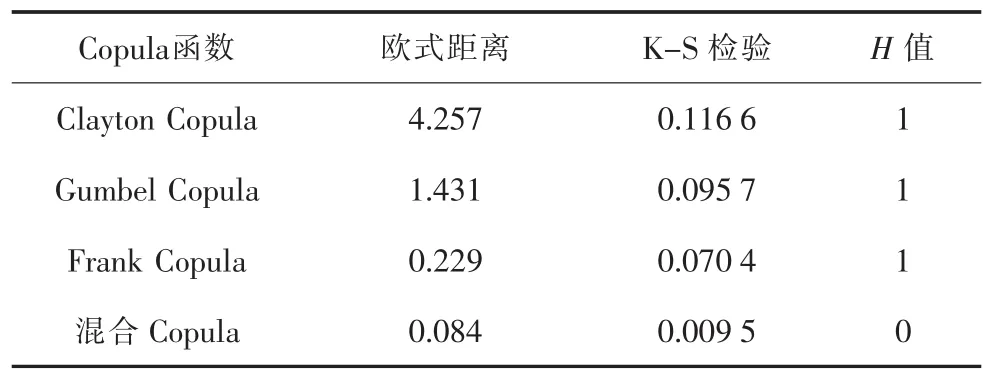
表2　风电场风速的拟合效果检验方法

由表2可知，与单一Copula分布函数相比，混合Copula分布函数具有最短欧式距离。根据K-S检验（H值），能通过K-S检验仅仅只有混合Copula函数（H=0），其他单一Copula函数（H=1）都没有通过K-S检验。因此相比单一Copula分布函数，混合Copula分布函数更合适描述2个风电场风速的相关结构。

3.2含多个风电场的发电系统可靠性评估

将同一地区两个容量为160 MW风电场接入到IEEE-RTS可靠性测试系统［17］中。由风速与输出功率之间的函数计算出风电机组的输出功率［6］。风电机组的切入、切出、额定速度分别为4.0 m/s、20.0 m/s、11.1 m/s，其强迫停运率为0.05［8，11］。

IEEE-RTS系统在2个风电场接入前后的系统可靠性指标如表3所示。缺电时间期望（LOLE）和电量不足期望（LOEE）［8，11］是评估发电系统可靠性的2个重要指标。其中，情况1为不考虑风电场风速之间的相关性；情况2为考虑风电场风速之间的相关性，并基于单一Copula函数法建立风电场风速相关性模型；情况3为考虑风电场风速之间的相关性，并基于混合Copula函数法建立风电场风速相关性模型。

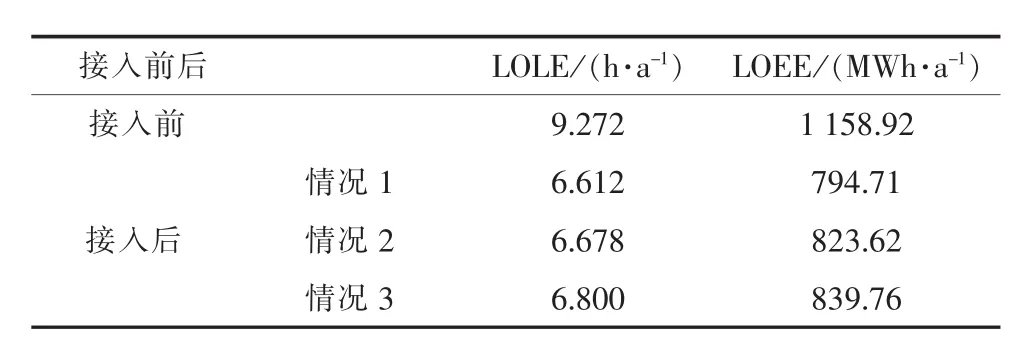
表3　IEEE-RTS系统在2个风电场接入前后的系统可靠性指标

由表3可知，在2个风电场接入IEEE-RTS系统后，其系统可靠性明显有所提高；发电系统中的风电场之间如不计风速相关性会造成含多个风电场发电系统可靠性的评估过于乐观。与此同时，混合Copula函数法和单一Copula函数法分别应用于含多个风电场发电系统可靠性评估中，与混合Copula函数法相比，单一Copula函数法也会高估风速之间相关性对系统可靠性产生的影响。

研究不同装机容量的2个风电场接入IEEERTS系统后其可靠性水平。针对不同容量的风电场，混合Copula函数法和单一Copula函数法分别应用于含多个风电场发电系统可靠性评估，其系统可靠性水平如表4、表5所示，两者之间的相对误差如表6所示。

表4　可靠性指标（混合Copula函数法）

表5　可靠性指标（单一Copula函数法）

表6　可靠性指标间的相对误差

由表4～6可知，随着风电场装机容量的增大，应用单一Copula函数法与混合Copula函数法得出系统可靠性指标之间的相对误差增大。综上所述随着越来越多风电场加入电力系统中，建立精确的风电场风速相关模型越来越重要。

4　结语

基于混合Copula函数建立了一种多元相关性风速模型，并在含多个风电场的发电系统可靠性评估中应用该模型。通过对多个风电场加入IEEE-RTS系统进行算例分析，与混合Copula函数法相比，单一Copula函数法高估了风速的相关性对系统可靠性的影响。由此可见，风电场风速相关性模型的精确程度是其系统可靠性评估计算中的关键因素，且所提出的混合Copula函数法在描述风电场风速相关性方面比单一Copula函数法更合适，更有优势。所建立的精确风速相关性模型为以后青岛地区乃至山东地区风电场的规划打下了理论基础。

［1］吴林伟，张建华，刘若溪.考虑风电机组故障的风电场可靠性模型及其应用［J］.电力系统自动化，2012，36（16）：31-35.

［2］刘威，赵渊，周家启，等.计及风电场的发输配电系统可靠性评估［J］.电网技术，2008，32（13）：69-74.

［3］吴昊，张焰，刘波.考虑风电场影响的发输电系统可靠性评估［J］.电力系统保护与控制，201l，39（4）：36-41.

［4］张硕，李庚银，周明.含风电场的发输电系统可靠性评估［J］.中国电机工程学报，2010，30（7）：8-14.

［5］XIE Kaigui，BILLITON R.Considering wind speed correlation of WECS in reliability evaluation using the time-shifting technique ［J］.Electric Power System Research，2009，79（4）：687-693.

［6］WANGDEEW，BILLITONR.Consideringload-carrying capability and wind speed correlation of WECS in generation adequacy as sessment［J］.IEEE Trans on Power Systems，2006，21（3）：734-741.

［7］FEIJOO A E，CIDRAS J，DORNELAS J L G.Wind speed simulation in wind farms forestay-state security assessment of electri cal power system［J］.IEEE Trans on Energy Conversion，1999，14（4）：1 582-1 588.

［8］秦志龙.计及相关性的含风电场和光伏电站电力系统可靠性评估［D］.重庆：重庆大学，2013.

［9］GEORGE Papaefthymiou，DOROTA Kurowicka.Using Copula for modeling stochastic dependence in power system uncertainly analysis［J］.IEEE Trans on Power System，2009，24（1）：40-49.

［10］徐玉琴，张林浩.考虑风速相关性的风电接入能力分析［J］.可再生能源，2014，32（2）：201-206.

［11］秦志龙，李文沅，熊小伏.考虑风速相关性的发输电系统可靠性评估［J］.电力系统自动化，2013，37（16）：47-52.

［12］韦艳华，张世英.Copula理论及其在金融分析上的应用［M］.北京：清华大学出版社，2008.

［13］庄丹琴.Copula函数的选择及其在金融分析中的若干应用［D］.马鞍山：安徽工业大学，2010.

［14］季峰，蔡兴国，王俊.基于混合Copula函数的风电功率相关性分析［J］.电力系统自动化，2014，38（2）：1-6.

［15］王小红，周步祥，傅利，等.基于综合Copula函数的风电功率相关性分析及其在无功优化中的应用［J］.可再生能源，2014，32 （8）：1 111-1 117.

［16］QIN Zhilong，LI Wenyuan，XIONG Xiaofu.Estimating wind speed probability distribution using kernel density method［J］. Electric Power Systems Research，2011，81（12）：2 139-2 146.

［17］BILLITON R，LI Wenyuan.Reliability assessment of electrical power systems using Monte Carlo methods［M］.New York：Plenum Press，1994.

Reliability Evaluation of Power System with Wind Farms Based on Mix-Copula Function

GAO Xiaotong1，QIN Zhilong2
（1.Jihongtan Reservoir Management Office of Jiaodong Water Diversion Project in Shandong Province，Qingdao 266001，China；2.State Grid Qingdao Power Supply Company，Qingdao 266002，China）

With the development of wind power，the relationship between the wind speed of wind farms has more and more influence on power system reliability.Based on mix-Copula functions，a model of multi-dimensional correlation wind speed is presented，and is applied to the IEEE-RTS reliability test system containing multiple wind farms.Through the example analysis，the mixed Copula function is more appropriate and has more advantages than single copula function for the description of the wind speed dependence structure.

wind speed correlation；mix-copula function；power system reliability；Monte Carlo simulation

TM732

A

1007－9904（2016）08－0025－04

2016-04-21

高小童（1985），女，工程师，从事水利、风电等清洁能源研究工作；秦志龙（1982），男，工程师，从事电网调度与控制的相关工作。