用纠缠态表象导出复杂量子介观电路的特征频率

笪　诚,范洪义

用纠缠态表象导出复杂量子介观电路的特征频率

笪诚1,2,范洪义1,3

（1. 巢湖学院数理工程研究中心, 安徽合肥 238000; 2. 巢湖学院机械与电子工程学院, 安徽合肥 238000; 3. 中国科学技术大学材料科学与工程系, 合肥 230026)

以讨论有互感和共用电容的两回路介观电路的量子化为例，我们提出复杂量子介观电路的特征频率的概念。在给出该电路正确的量子Hamilton 算符后，用纠缠态表象求出了系统在恒稳电路状态下的能量量子化公式以及特征频率，发现互感越大，特征频率越高。文中同时也得到了系统的波函数和零点能，这在经典框架中是无从顾及的。

纠缠态表象；介观电路；正则变换；特征频率

0　引 言

随着微电子学和纳米技术的飞速发展，尤其是许多高新技术诸如隧道扫描显微镜（STM）等的发展和应用，电路集成度的大幅度提高及电子器件的日益小型化，其集成单元间的空间尺寸已达原子量级。显而易见，当荷电粒子的非相干长度达到费米波长量级时，以粒子的整体平均运动为基础的经典器件的物理学将不再适用，或者说当电子输运尺度达到电子两次非弹性碰撞之间的尺度时必须考虑电路和器件的量子效应[1]，由此对介观物理量的量子特性的研究变得越来越重要，这对于进一步设计微小电路，压低噪声影响具有重要的指导意义。

上个世纪80年代，Louisell首先考虑了LC单回路的量子化，获得了真空态的量子噪声[2]。进入本世纪以来，有很多文章研究复杂介观电路的量子化、噪声和量子涨落[3-10]，如顾永建发展了一种有源RLC电路的量子化方案并研究了压缩真空态下介观RLC电路中电流和电荷的量子涨落[4]；王继锁等人基于介观电路中电荷应是量子化的这一基本事实，给出了介观电感耦合电路的量子理论和库仑阻塞条件，并讨论了该介观电感耦合电路的量子涨落[6]；汪仲清利用热场动力学的方法研究了介观RLC电路在具有热噪声的真空态下电荷和磁通（电流）的量子涨落,从而得到了有限温度下这一电路在热真空态下的量子涨落与温度的关系[8]；龙超云等人给出耗散介观电容耦合电路的量子化，并在此基础上研究电荷和电流在能量本征态下的量子涨落[10]。但以往的研究都没有讨论复杂电路作为一个整体的特征频率。其原因是在经典电路理论的框架内没有量子效应，人们只需根据基尔霍夫定律求出电路的电流、电压和阻抗损耗就可以了。本文中，我们讨论有互感M和共用电容C的两回路介观电路的量子化。在给出其正确的量子Hamilton 算符后，用纠缠态表象求出了系统在恒稳电路状态下的量子化能级公式以及特征频率

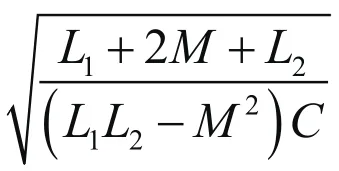
这表明特征频率随着互感增大而增大；当互感为零时，即两个回路的电感彻底分离，互不影响，此时特征频率变为

1　描述系统的Lagrange量、Hamilton量和正则变换

考虑如图1所示的有互感和共有电容的两回路介观电路，两个电感之间有互感，电路的一端有电源,

图1　有互感和共有电容的两回路介观电路

从两个回路的电流方程可以看出拉氏函数为[11]

K代表漏磁程度，K越大表明漏磁越小，通常K<1。由式(1)得到

根据Lagrange方程

对于回路1来说我们就有

同理，回路2的Lagrange方程为

这与用Kirchhoff定理[12]得出的回路的动力学方程一致。说明(1)式确定的系统拉氏量是正确的。qi的正则动量为

对Lagrange量作Legendre变换，注意到式(10)，得到Hamilton量

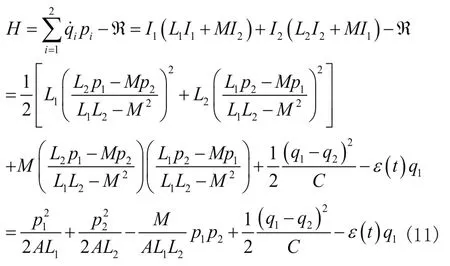
这里

以下我们只考虑稳恒电路的情况，即假定电流已经达到恒定，外源的贡献(t)q1ε正好抵消电路中产生的焦耳热。所以在下面的讨论中我们可以认为系统的量子化哈密顿量不显含时间t

我们的目的是求其能量量子化公式、零点能及特征频率，因为p1p2与q1q2项都会引起量子纠缠，我们将用纠缠态表象来实现目标。

2　两个互为共轭的纠缠态表象

令

这里已取===.引入一个双模Fock空间，其产生（湮灭）算符为。引入态矢量

我们可以证明它是p1+p2及q1-q2的共同本征态，[p1+p2，q1-q2]=0。事实上，用a1,a2分别作用于上有

由此导出

可见η的实部和虚部分别对应q1-q2和p1+p2的本征值。可以用有序算符内的积分技术（IWOP技术）和:简捷地证明满足完备性[13-16]

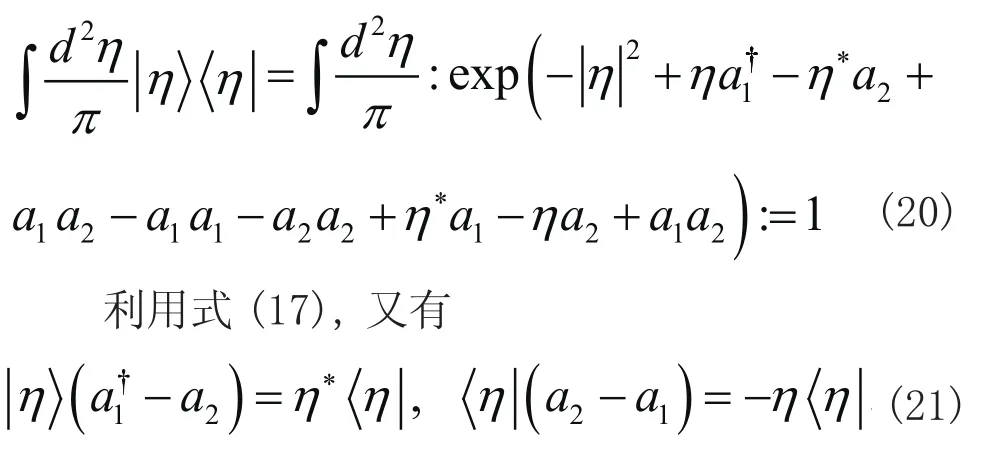
由式(17)及(21)得到

定义

则有

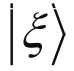
由此给出

考虑到

利用式(35)和(36)有

于是

因此

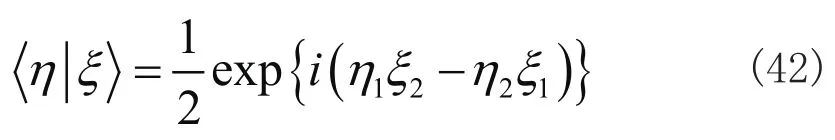
3 用纠缠态表象求解有互感和共有电容的两回路介观电路的能级

现在我们在纠缠态表象内求解有互感和共有电容的两回路介观电路的特征频率。由式(36)可得

则有

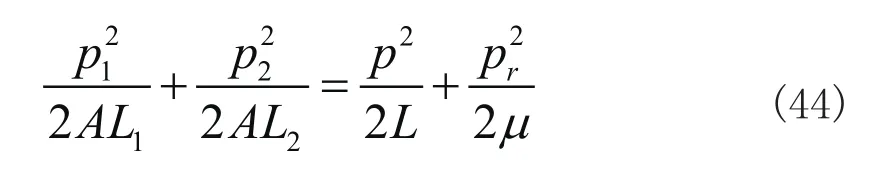
系统的Hamilton量可以写为

再由式(43)可导出

待求，则由

可得关于Ψn的微分方程

再令Ψn形为

则方程(50)中的前两项可写为

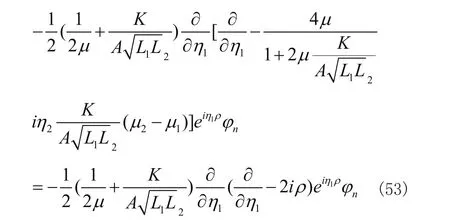
再由

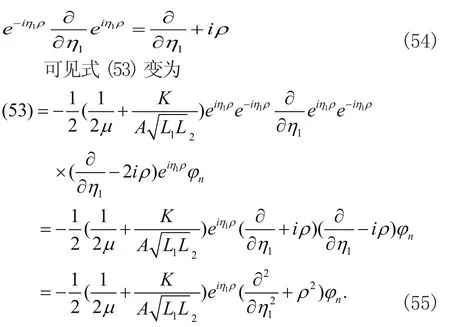
代入方程(50)可得nϕ所满足的方程

把上式与量子简谐振子定态方程

4　讨论和分析

分别为孤立单回路1和单

回路2的特征频率，这也是所期望的。

图2　零互感有共有电容的两回路介观电路

通过对此复杂电路的量子化，我们引入了整个电路的量子特征频率的概念并用纠缠态表象求出了它。同时系统在纠缠态表象内的波函数可结合式(48)、(51)及谐振子的波函数[17]

而给出

其中,Hn为Hermite多项式。此文的讨论还有望推广到其它电路。

附录A1

为了进一步验证方程(60)中特征频率的正确性，我们再将(13)式中的Hamilton量对角化。

我们采用不久前提出的不变本征算符方法（见文献[18]）来完成这一任务。文献[18]给出了对角化一般形式二次型Hamilton量的步骤。对比标准式(62)和式(13)中的Hamilton量，我们写下对应的L矩阵和M矩阵

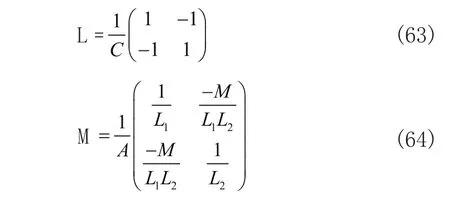
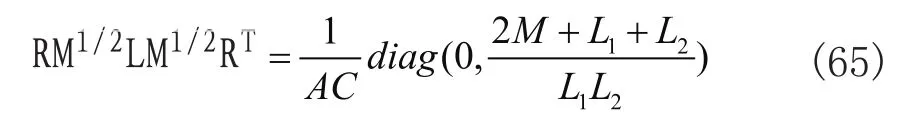
根据文献[18]，正则变换后的简正坐标和动量为

于是变换后的哈密顿量

可见等效的简正频率为

与我们用纠缠态表象计算出来的结果一致。

[1]Bout F A. Mesoscopic physics and nanoelectronics: nanoscience and nanotechnology [J]. Phys.Rep 1993,234(2-3):73-174.

[2]Louisell W H.Quantum Statestical Properties of Radiation [M].New York: John Wiley,1973.

[3]Xu X L, Wang X X, Fan H Y. Energy variation of mesoscopic L C electric circuit in external electromagnetic field [J].Int. J. Mod. Phys. B, 2015,29(23): 1550169-8.

[4]顾永建.压缩真空态下介观RLC电路中电荷和电流的量子涨落[J].物理学报,2000,49(5): 965-968.

[5]Zhang S, Zhao Y F, Jing X G,et al. Quantum Fluctuations of a Mesoscopic Capacitance Coupled Circuit with Power Source[J]. Chin. Phys. Lett., 2003, 20(4):561-563.

[6]王继锁,冯健,詹明生.无耗散介观电感耦合电路的库仑阻塞和电荷的量子效应[J].物理学报, 2001,50(2): 299-303.

[7]Liang B L, Wang J S, Meng X G, et al. Quantum entanglement and control in a capacitively coupled charge qubit circuit[J]. Chin.Phys.B, 2010,19(1): 010315-7.

[8]汪仲清.介观RLC电路在热真空态下的量子涨落[J].物理学报,2002,51(8):1808-1810.

[9]Wang J S, Feng J, Zhan M S. Quantum fluctuations of a non-dissipative mesoscopic inductance coupling circuit in a displaced squeezed Fock state[J]. Phys. Lett. A, 2001(281):341-346.

[10]龙超云, 刘波, 王心福. 耗散介观电容耦合电路的量子涨落[J].物理学报,2002,51(1): 159-162

[11]Goldstein H .Classical Mechanics [M]. Massachusetts:Addison-Wesley,1980.

[12]Nilsson J W, Riedel S A. Electric Circuits [M]. Massachusetts:Addison-Wesley,1999.

[13]范洪义.量子力学纠缠态表象及应用[M].上海: 上海交通大学出版社,2001.

[14]Da C, Cheng Q F, Zhang P F, et al. Time evolution law of the Laguerre-polynomial-weighted chaotic photon field in an amplitude-damping channel[J]. Can. J. Phys., 2015,93(3):283-289.

[15]范洪义.量子力学表象与变换论—— 狄拉克符号法进展 [M].第二版.合肥: 中国科学技术大学出版社,2012.

[16]Da C, Chen Q F, Fan H Y. Evolution Law of the Negative Binomial State in Laser Channel and its Photon-Number Decay Formula[J].Int. J. Theor. Phys.,2014,53(12):4372-4380

[17]R Shankar. Principles of Quantum Mechanics [M].2nd Ed..Beijing: World Publishing Corporation,2007.

[18]Fan H Y, Chen J H, Yuan H C. Applying invariant eigen-operator method to deriving normal coordinates of general classical Hamiltonian [J]. Chin.Phys.B, 2010,19(9):090312-5.

Obtaining Characteristic frequencies of complex quantum mesoscopic circuit through the entangled state representation

DA Cheng1,2, FAN Hongyi1,3
(1.The Interdisciplinary Center for Study on Maths, Physics and Engineering, Chaohu University,Hefei, 238000, China; 2.School of Mechanical and Electronic Engineering, Chaohu University, Hefei, 238000, China; 3.Department of Material Science and Engineering, University of Science and Technology of China, Hefei, 230026, China)

By discussing quantization of a two-loop quantum mesoscopic circuit in which a capacitance is sharing and mutual inductance exists between two inductances, we propose the conception of characteristic frequency for complex electric circuit in the context of quantum mechanics. In the steady case of the circuit, after the quantum Hamilton operator is correctly deduced, and by using the entangled state representation we derive the energy quantization formula and the characteristic frequency of the system. It shows that the greater the mutual inductance, the higher the characteristic frequency. At the same time, the wave function and zero point energy are also obtained, which are impossible to be taken into account in the classical framework of the system.

entangled state representation, mesoscopic circuit, canonical transformation, characteristic frequency

0413.1

A

2095-8382(2016)03-073-08

10.11921/j.issn.2095-8382.20160316

2016-04-07

安徽省高等学校自然科学研究重点项目（项目编号：KJ2016A504）；安徽省高等学校省级质量工程教学研究项目（项目编号：2015jyxm327）；巢湖学院博士科研启动基金资助项目（项目编号：KYQD—201407）

笪诚（1974-），男，博士，讲师，安徽桐城人,主要研究方向：量子光学、量子力学。