基于GA-BPNN的MPPT控制方法与P&O的比较

金焱飞，张会林，张　松，史超然，李荣伟

(上海理工大学 光电信息与计算机工程学院，上海 200093)



基于GA-BPNN的MPPT控制方法与P&O的比较

金焱飞，张会林，张松，史超然，李荣伟

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对传统光伏电池阵列控制方式在复杂天气环境下，对最大功率点跟踪效果不理想的现象。设计了一种基于GA-BPNN的改进型恒压光伏MPPT控制算法，并通过搭建基于GA-BPNN的改进型恒压光伏MPPT的仿真模型，再与传统P&O控制方法进行比较分析。仿真结果证明，该算法能准确快速地在复杂天气环境下进行最大功率点跟踪，且性能稳定。

光伏电池阵列；BP神经网络；遗传算法；干扰观测法

由于传统能源的消耗给生态环境带来了重大的破坏，使国家经济社会发展面临资源匮乏和污染加剧的双重考验[1]。太阳能作为可再生绿色能源，因其无污染、低成本、易获取的特点，已成为代替传统能源的首选能源[2]。现如今光伏阵列作为光伏发电系统中不可或缺的一个组成部分，其转换效率和稳定性显得尤为重要。为了使光伏阵列达到最佳转换效率，且能应对各种复杂的气象环境，本文设计了一种基于GA-BPNN的最大功率点跟踪技术。最后，通过搭建Matlab/Simulink仿真模型，分析比较了干扰观测法和基于GA-BPNN的控制方法，结果表明基于GA-BPNN的控制方法可以弥补干扰观测法的不足。

1　光伏电池板的等效模型

本文采用一种新型的四参数光伏阵列模型[3]，模型的等效电路如图1所示，其数学表达式

(1)

其中，Iph表示光生电流；I0表示反向饱和电流;Rs表示光伏电池串联等效电阻；n是理想因子，Ut=kq/T，其中k是波尔兹常数，k=1.381×10-23J/K，q是电子电荷量，q=1.602×10-19C，T是光伏电池温度。

图1　光伏电池等效电路

当光伏电池短路时，I=Isc，U=0，由此可得

Iph=Isc

(2)

当光伏电池开路时，I=0，U=Uoc，由此可得

(3)

当光伏电池的输出处于最大功率点时，I=Im，U=Um，由此可得

(4)

(5)

为应对各种复杂环境，需不断对光照强度和温度公式进行修正，修正公式如下[4]

(6)

(7)

(8)

(9)

其中，M为修正系数；a为短路电流温度系数；b为开路电压温度系数，其他具体参数均可由制造商提供的技术文件获得，本文将光照强度Gref=1 000 W/m2，温度Tref=25 ℃设置为外部环境的参考状态。

基于上述数学模型，本文在Simulink上搭建了带修正的新型光伏电池仿真模型，并通过此光伏电池模型得到电流I-电压V，功率P-电压V的特性如图2所示。

图2　不同光强和温度时的特性曲线

2　干扰观测法

干扰观测法是目前使用最多的MPPT方法之一，其原理是光伏电池先给出一个输出电压Uo，接着再调节升压电路开关管的占空比，来实现对输出电压的周期性扰动，比较前后功率的大小[5]。若功率随着输出电压的变化而相向变化，则说明此时的功率点在最大功率点的左侧，反之亦然。经过反复的扰动判断，工作点会越来越接近最大的功率点[6]。

本文根据干扰观测法的控制算法，在Matlab/Simulink中建立了一个定步长的干扰观测法控制的MPPT仿真模型。

3　基于GA-BPNN的MPPT控制系统

扰动观测法由于需不断地扰动来判断是否在最大功率点，所以并不能稳定在该点处。当外部环境发生突变，P&O控制方法就不能准确判断出输出功率的变化原因，从而导致最大功率点的跟踪方向出现错误，最终使电压和功率崩溃，使系统出现严重的震荡现象，所以本文提出基于GA-BPNN的新型最大功率点跟踪方式。

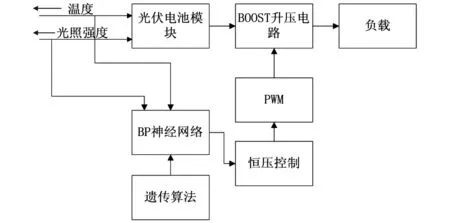
图3　基于GA-BPNN的光伏MPPT结构图

首先通过采样当前的环境温度和光照强度，再将这两组数据传给经BP遗传算法优化的神经网络，得到最优电压值，最后再将获得的优化电压值作为恒电压控制方法的恒定电压参数，从而实现复杂环境下仍能准确快速的追踪到最大功率点。其结构图如图3所示。

3.1BP神经网络

BP神经网络可通过从真实的具有广泛代表性的数据中归纳出基于采样数据的预测模型，BP神经网络的算法可分为神经网络的构建、神经网络的训练、神经网络的预测3部分。本文中是根据外界的温度和光照强度来预测此时的最佳工作电压，既输入层有温度和光照强度两个节点，输出层是最佳电压一个节点。本文通过试凑法来确定隐含层的最佳节点数，试凑法的公式如下[7]

(10)

其中，M是输入层神经元个数；L是输出层神经元个数；α是1～10之间的常数；Q是隐含层的神经元个数。经过反复测试和结合实际情况，最终确定了隐含层有5个节点。

文中采用上述新型光伏电池仿真模型，记录了60组在不同时刻下环境温度、光照强度和最大功率点的电压。再通过Matlab训练光伏MPPT控制的神经网络，将光照强度和外界环境的温度作为输入，最大功率点的电压作为输出，随机选取51组数据作为网络的训练数据，其余的9组作为网络测试数据，构建好的神经网络。

文中选用Trainlm函数对网络进行训练，隐含层的传输函数选为Tansing函数，输出层的传输函数选为Purelin函数，最大训练设置为3 000步，误差指标为0.01。

3.2遗传算法优化的神经网络

本文采用遗传算法对神经网络的3个部分进行优化[8]：首先通过输入和输出参数的个数来确定神经网络结构；然后使用遗传算法计算出适应度值和一系列遗传操作得到最优个体，且其可对神经网络的初始权值和阈值进行赋值；最后通过优化的神经网络预测输出。

上文已经确立了网络结构为2-5-1型，共有2×5+5×1=15个权值，5+1=6个阈值，本文选择的遗传算法的个体编码长度为15+6=21。采用BP神经网络预测输出与期望输出的误差绝对值和作为适应度函数F公式如下

F=k(abs(yi-oi))

(11)

文中采用轮盘赌法作为遗传算法的选择操作，每个个体的选择概率Pi为

(12)

对实数编码个体进行交叉操作的方法如下[9]

(13)

再选取第i个个体的第j个基因aij进行如下的变异操作

(14)

其中，yi和oi分别是第i个节点的期望输出和神经网络预测输出；fi=k/Fi;N是种群个体数目；b和r是[0,1]之间的随机数[10]，f(t)=r(1-t/Tmax)；t是指当前迭代的次数，Tmax是指最大进化的次数。

遗传算法的具体运行的参数如下：种群规模数为10，交叉概率为0.4，终止进化次数为30，变异概率为0.2。进化结束后将遗传算法得到的最优个体赋值到神经网络中。

4　仿真分析

为验证所设计基于GA-BPNN控制的MPPT比传统的控制方式要优越，文中搭建了基于GA-BPNN控制的光伏系统MPPT仿真模型如图4所示。仿真参数具体设置为：环境温度为25 ℃，光照强度设置为1 000 W/m2和800 W/m2，仿真时间设置为0.02 ，在启动时光照强度设置为1 000 W/m2，接着在0.01 后将光照强度转换成800 W/m2。

该系统采用GA-BPNN控制方式，使光伏电池输出电压始终保持在其最大功率点处。光伏电池与后续的升压电路之间用一个容量为100 μF大电容连接，将此大电容作为Boost电路的直流源。本文中考虑到一定的裕量将Boost电感设置为10 mH，整个系统的负载设置为5 Ω。仿真结果如图5(a)所示，图5(b)是基于干扰观测法控制的系统仿真图。

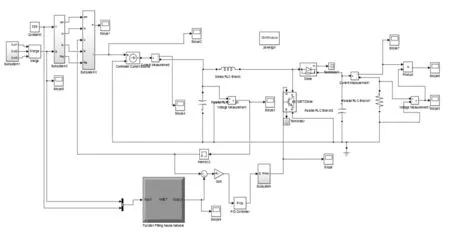
图4　基于GA-BPNN控制算法的光伏系统MPPT仿真模型

(a)　基于GA-BPNN的仿真图

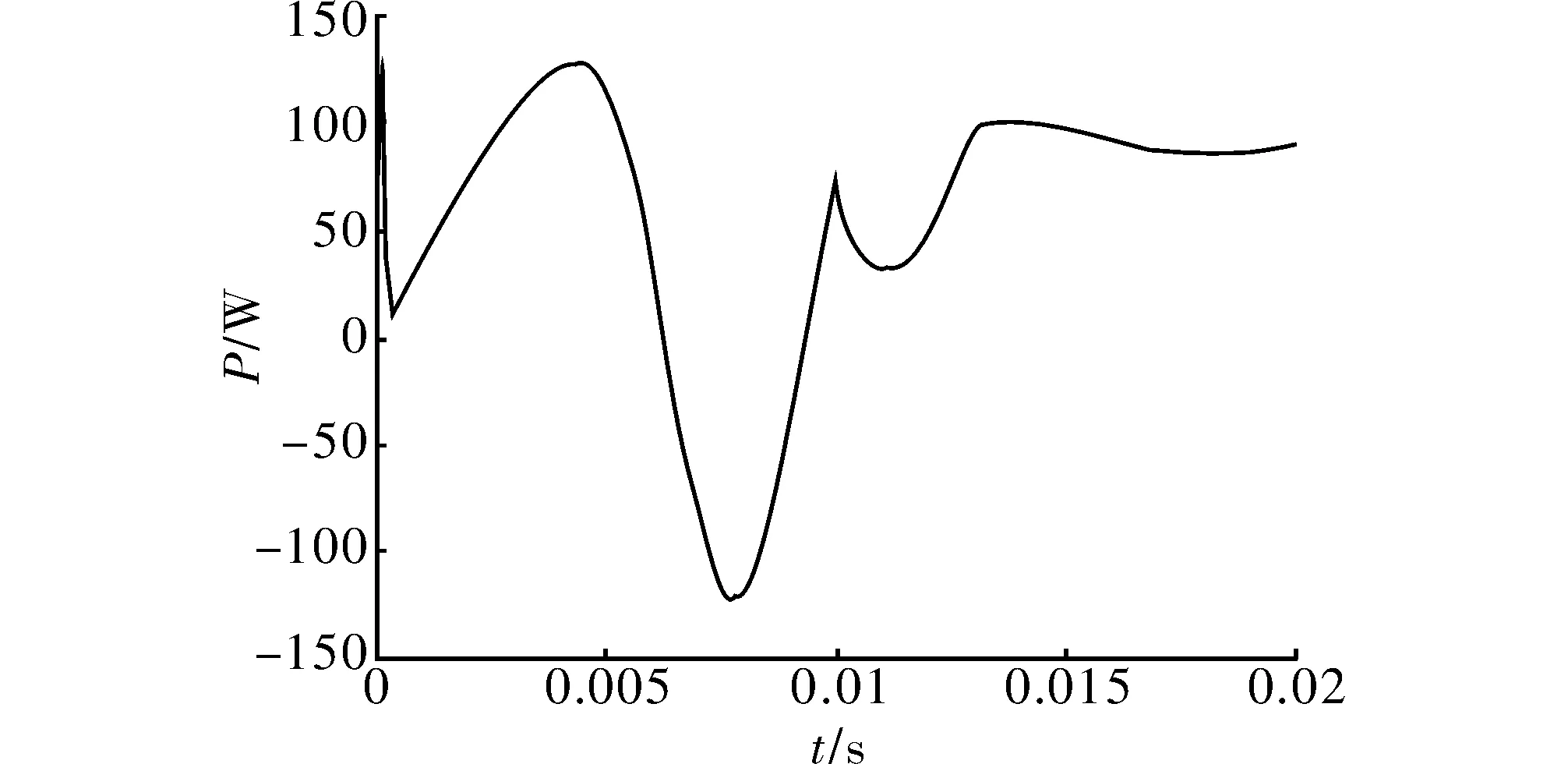
(b)　基于干扰观测法的仿真图图5　干扰观测法控制系统仿真图

比较图5(a)与图5(b)可发现，在1 000 W/m2光照强度的环境下，系统还没有追踪到最大功率点，光照强度突然从1 000 W/m2转换成800 W/m2时，系统会出现严重的震荡现象，而基于GA-BPNN控制的系统则会较为平稳的过渡，并相比于干扰观测法，其还可快速的追踪到最大功率点。究其原因，基于GA-BPNN的控制算法，正是由于拥有遗传算法的过程，从而能克服P&O控制方法不能适应各种复杂环境的缺点。

比较两图发现时间经过0.01 s后，图5(a)中的功率值能够稳定在100 W处，然而在图5(b)中的功率值却总在100 W左右摆动。这是由于基于GA-BPNN的控制算法需通过不断的扰动来判断其现在是否处于最大功率点，所以在光照强度稳定时，输出的最大功率也较为稳定。

5　结束语

本文针对复杂气象环境下传统的MPPT控制方法不能准确的追踪到最大功率点问题，设计了基于GA-BPNN的MPPT控制系统。通过对比和分析两种控制方式下的最终仿真波形图，结果验证了GA-BPNN具有应对复杂气象环境的能力。

[1]李营.基于分段模糊控制方法的光伏MPPT控制策略研究[J].机电工程技术,2015, 44(8):82-86.

[2]张正文,谭文龙,潘甲,等.狼群搜索算法在光伏阵列MPPT中的应用[J].河南科技大学学报:自然科学版,2015,36(5):57-61.

[3]杨永恒,周克亮.光伏电池建模及MPPT控制策略[J].电工技术学报,2011,26(S1):229-234.

[4]Aissa Chouder,Santiago Silvestre,Nawel Sadaoui,et al.Modelling and simulation of a grid connected PV system based on the evaluation of main PV module parameters [J].Simulation Modelling Practice and Theory,2012,20(1):46-58.

[5]肖伸平,曾钰,赵培哲.改进干扰观测法在光伏发电系统MPPT中的应用[J].新型工业化,2014(4):45-50.

[6]张毅,帕孜来·马合木提,徐立亮.改进3点权位法的光伏电池MPPT控制器的应用研究[J].电气传动,2015,45(6):65-68.

[7]Veerachary M,Senjyu T,Uezato K. Neural network based maximum power point tracking of coupled-inductor interleaved-boost-converter-suppied pv system using fuzzy controller[J].IEEE Transactions on Ind Electronics,2003,50(4):749-758.

[8]王小川,史峰,郁磊,等.Matlab神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013.

[9]朱献文.基于遗传算法和Hopfield神经网络的字符识别方法[J].电子设计工程,2011,19(18):57-59.

[10] 王德明,王莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报:工学版,2012,46(5):837-841.

Comparison of MPPT Control Methods Based on GA-BPNN and Perturb & Observe Algorithm

JIN Yanfei, ZHANG Huilin, ZHANG Song, SHI Chaoran, LI Rongwei

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

This paper introduces a modified constant pressure PV MPPT control algorithm based on GA-BPNN for better power point tracking effect than traditional control method under complex weather conditions. The simulation model of a modified constant pressure PV MPPT control algorithm based on GA-BPNN is constructed and compared with the P&O control method. The result shows that the algorithm can track maximum power point accurately and quickly with better stability and higher precision.

photovoltaic array; BP neural network; genetic algorithm; disturbance observation method

10.16180/j.cnki.issn1007-7820.2016.08.042

2015-11-18

沪江基金资助项目(B1402/D1402)

金焱飞(1991-)，男，硕士研究生。研究方向：电力电子与电力传动。

TM914.4+3; TP391

A

1007-7820(2016)08-145-04