一种改进的各向异性扩散模型

刘　彪

(西安电子科技大学 数学与统计学院，陕西 西安 710126)



一种改进的各向异性扩散模型

刘彪

(西安电子科技大学 数学与统计学院，陕西 西安 710126)

各项异性扩散方程是一种经典的图像去噪方法，但该方法在去除噪声的过程中会造成一定程度的模糊边缘。对此文中提出了一种基于改进的各向异性扩散方程的图像去噪方法，通过在其能量泛函的目标函数中添加残差项，使能量泛函的极小解更加接近原始的函数，可取得比其更好的去噪效果。文中方法可看作是各项异性扩散方程和全变差模型的结合。实验表明，新提出的方程相对经典的方程有较好的边界处理效果和更高的信噪比。

各项异性扩散；图像光滑化；能量泛函；偏微分方程

图像是人类社会有力的通讯媒介之一，在生活和研究中占据很大的重要性。但是图像在传递过程中，不可避免地会受到噪声的干扰。图像去噪作为图像处理领域[1-2]重要的问题之一，主要目的是在去除噪声的同时保护图像本身的细节边界等信息。目前已经有多种图像去噪的方法，主要有基于变分和偏微分方程的方法，经典的方法有热方程[3]，各向异性扩散方程[4]，TV模型[5-6]，且在其的基础上发展出了诸多的模型[7]。这些方法可去除噪声，但仍会一定程度的造成图像的边缘的模糊。

本文在经典的各向异性扩散方程P-M[8]方程(Perona-Malik)的基础上，对其进行改进。经典的P-M方程可看作一个特殊的能量泛函的欧拉方程，求欧拉方程的过程就是一个求能量泛函极小的过程。本文在P-M模型的能量泛函中添加残差项(忠诚项)，这是为了使其能量泛函的极小解更加接近原始的图像。当然，全变差模型TV模型[7](Total Variation Model)的能量泛函本来含有残差项与正则项的。因此这种改进方法也可以看作是P-M方程和TV模型的结合。并且在本文中给出了数值算法流程，并对比了改进算法与原始P-M模型。

1　一种新的各项异性扩散模型

1.1P-M方程

文中了解P-M方程是图像去噪算法中重要的一种模型，其是传统的热扩散方程的一个推广，具体的方程如下

(1)

其中，c(|u|2)是一个扩散系数，其依赖于图像的梯度。当c(|u|2)=1时，模型退化为热方程，即高斯光滑滤波。P-M方程在其基础上进行改进。将扩散率函数c(|u|2)推广为梯度u的函数，热方程可看作是各项异性扩散模型的一个特殊的形式。通过适当定义扩散率函数c(|u|2)的形式，可调节P-M模型对图像的扩散的作用，使得其既去噪又能较好的保护边缘。

当然，该方程可看作是求一个能量泛函极小化的能量耗散过程，用变分的方法可通过能量泛函极小化得到偏微分方程的形式。能量泛函有如下形式

(2)

其中，φ(·)≥0是一个关于梯度的增函数，其与P-M方程中的扩散系数有如下关系

(3)

这里的s表示梯度模值的平方

s=|u|2

(4)

通过对式(2)进行求解，得到欧拉方程为(因为能量泛函极小化的求解可看作其关于u的导数为0)

div(c(|u|2)u)=0

(5)

用最速下降法解决这一方程便可得到传统的P-M方程。

1.2P-M方程的推广

本文对上述方程进行改进，在Perona 和Malik提出的各向异性扩散方程的基础上，在能量泛函中添加残差项。这样会使得改进模型相比较P-M方程更加接近原始的图像，保留图像的主要特征。这样能量泛函方程式(2)变为

(6)

其中，L2(Ω)是能量有限函数或图像空间；f是退化图像；u是原始真实图像。当然，函数φ的形式取作不同的函数，模型的效果也不同。

求解上述改进的能量泛函式(6)的欧拉方程，即能量泛函的极小解。文中讨论退化过程中只有噪声，则有

(7)

求极小即导数为0，可得到等价的形式

div(c(|u|2)u)+λ(f-u)=0

(8)

此欧拉方程式(8)可用最速下降法求解，得到的改进各项异性扩散模型，如式(9)所示的形式

(9)

在求解中，方程中的λ可调节忠诚项和正则项的作用。

对于方程中扩散率函数c(|u|2)，需要满足一些条件才能保证方程的有效性，本文列举几种经常用到的扩散率函数的形式

(10)

这种情况下的扩散方程(9)是一个光滑型的偏微分方程，可去除噪声。若扩散率函数取

(11)

或

c(s)=e-s/k

(12)

这也是Perona和Malik提出的两个函数，由于函数的性质，这两种函数式(11)和式(12)可去除噪声并保护边缘。

若与TV模型相比较，TV模型中的扩散率函数可看作(10)中的函数。本文选用扩散率函数(11)作数值仿真实验。所以，本文提出的模型可看作是PM模型和TV模型的一个结合，可以取得比二者更好的结果。

1.3数值算法

在计算机中的数字图像处理中，图像是以二维矩阵的形式存储和处理的。对于本文提出的模型式(9)，可用差分的方法对图像进行扩散，用差分近似函数的梯度。对于二维图像，计算4个方向的差分

(14)

然后通过差分近似计算梯度，从而计算扩散率函数，具体的算法流程如图1所示。

图1　算法流程图

按照流程图1对图像进行迭代，不断更新图像中每个点的像素值。当新旧图像中的像素值的变化小于某个值时，迭代停止，用最后得到的像素值代替原来对应的像素值，就得到了处理后的结果。同时，恢复图像的PSNR值也达到最优。

2　数值试验

接下来，对所提算法的有效性进行说明，对比文中提出的新算法和原始的各向异性扩散模型。在图2中对比了本文的算法与PM模型对Lena图的处理结果，如图2所示，文中算法可取得更好的视觉效果。为更直观的对比，在表1中列举了两种算法的比较的PSNR值，从表中也可看出，文中的算法取得了更高的PSNR值，说明该算法的有效性。

图2　去噪效果对比图

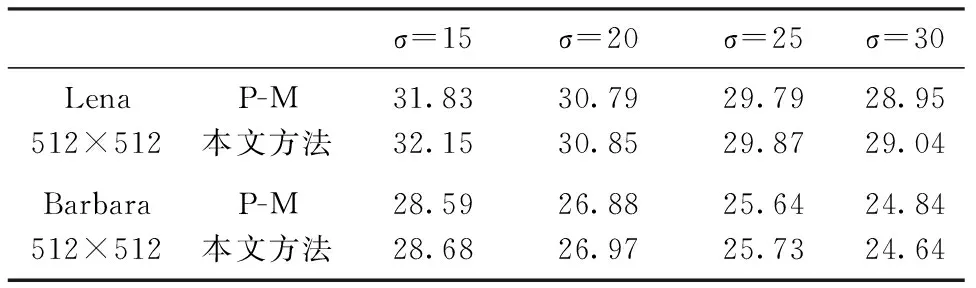
σ=15σ=20σ=25σ=30Lena512×512P-M本文方法31.8332.1530.7930.8529.7929.8728.9529.04Barbara512×512P-M本文方法28.5928.6826.8826.9725.6425.7324.8424.64

3　结束语

文中给出了一种基于各向异性扩散方程的新图像处理方法。其可看作是一个能量泛函的欧拉方程，因此P-M模型也可看作是一个能量泛函极小化的过程。本文提出的算法能量泛函是在P-M模型能量泛函的基础上添加忠诚项得到的。所以，可将其看作是对P-M模型的一种推广，可取得比传统P-M模型更好的去噪效果。被推广后的能量泛函的形式与TV模型的能量泛函的形式类似，文中算法可看作是P-M模型和TV模型的一个结合。

因图像可看作是一个二维的离散的函数，所以需要运用差分的方法近似得到不同点的导数，本文给出了模型的算法流程。为验证算法的有效性，在最后对这种算法进行了数值仿真实验。可从数据中看到，这种模型比原始P-M模型和TV模型均取得了更高的PSNR值，且视觉效果更好。

[1]Buades A,Coll B,Morel J M.Image denoising methods with A new nonlocal principle[J].SIAM Review,2010,52(1): 113-147.

[2]Buades A,Coll B,Morel J M.A review of image denoising algorithms, with a new one[J]. Multiscale Modeling & Simulation,2005,4(2): 490-530.

[3]Lindenbaum M,Fischer M,Bruckstein A. On Gabor’s contribution to image enhancement[J].Pattern Recognition,1994, 27(1):1-8.

[4]Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

[5]Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J]. Physica D:Nonlinear Phenomena,1992,60(1): 259-268.

[6]Osher S,Solé A,Vese L.Image decomposition and restoration using total variation minimization and the H 1[J].Multiscale Modeling & Simulation,2003,1(3):349-370.

[7]Catté F,Lions P L,Morel J M,et al.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal on Numerical Analysis,1992,29(1):182-193.

[8]Weickert J.Anisotropic diffusion in image processing[M].Stuttgart:Teubner,1998.

[9]Weickert J,Romeny B M T H,Viergever M. Efficient and reliable schemes for nonlinear diffusion filtering[J].IEEE Transactions on Image Processing,1998,7(3):398-410.

A New Modified Anisotropic Diffusion Equations

LIU Biao

(School of Mathematics and Statistics，Xidian University, Xi’an 710126, China)

The anisotropic diffusion equation is a classical image denoising method, but this method can cause a certain degree of fuzzy edge in the process of removing noise. This paper presents a based on improved anisotropic diffusion equation for image to denoising method, through in the objective function of the energy functional add residuals and make the energy functional minimizer is closer to the original function can get better denoising effect. The method can be regarded as the combination of the anisotropic diffusion equation and the total variation model. Experiments show that the new equation has better boundary treatment effect and higher signal to noise ratio than the classical equation.

anisotropic diffusion; image smoothing; energy functional; differential equation

10.16180/j.cnki.issn1007-7820.2016.08.038

2015-11-24

刘彪(1989-)，男，硕士研究生。研究方向：图像处理等。

TP391.41;O24

A

1007-7820(2016)08-130-03