基于小波分解的计算机图像去噪算法

张　洋

(1.中国人民大学，北京 100872；2.北京信息职业技术学院 专业部，北京 100070)



基于小波分解的计算机图像去噪算法

张洋1,2

(1.中国人民大学，北京 100872；2.北京信息职业技术学院 专业部，北京 100070)

计算机图像在形成过程中较易受到外界因素的干扰而形成噪声，对图像质量噪声较大的影响，小波分解可对图像信号在频域中进行细致的划分，选择合适的阈值可实现图像去噪的目的。文中分别对图像质量，小波分解、Mallat算法和小波阈值去噪进行阐述，并利用Matlab仿真软件对应用小波分解的图像信号进行去噪。仿真结果表明，该方法具有较好的图像去噪效果。

小波分解；图像去噪；Mallat算法；小波阈值；Matlab仿真

计算机图像处理技术在多领域的广泛应用，如超声波图像处理、智能轨道交通、水印防伪技术、人脸与虹膜识别、X光照片图像处理等方面[1]。

由于计算机图像在其信号形成的同时会受到来自外界的干扰或仪器自身因素的影响，易形成图像噪声，从而对人们准确的认知原始图像信号造成了一定干扰，并对之后的计算机图像处理产生较大影响[2]。计算机图像的去噪也称为计算机图像滤波，是希望通过采用某种算法或者运算以实现提高图像质量的目的。计算机图像去噪的方法众多，例如邻域平均法、空间域低通滤波法、中值滤波法和维纳滤波法等，相比于其他的滤波方法，小波分解方法可较好地对计算机图像进行频域分解，并从频域角度对计算机图像的噪声进行滤除，能取得较好的去噪效果[3]。

1　图像质量

在进行计算机图像去噪之前，首先应对计算机图像质量进行分析，计算机图像质量分析是计算机图像处理学的基础。计算机图像质量可从两个方面进行阐述，一方面是计算机图像逼真程度，即被处理的计算机图像对象和原始图像之间的偏离程度；另一方面就是计算机图像的可识别程度，即图像处理人员从图像中可获取信息的能力[4]。

对计算机图像质量的评价可分为主观评价和客观评价两种。计算机图像质量的主观评价是以人的视角对计算机图像进行观察分析，从主观角度评价计算机图像质量的优劣，再应用统计学方法对评分进行平均处理，最终得到评价结果。因存在评价人的主观因素，所以进行统计分析时，要对评价人的图像技术经验水平进行考虑，同时进行评价人的数量也不应过少，避免测试条件和图像本身质量不匹配。计算机图像质量的客观评价存在多种方法，主要方法是图像的逼真度测量，通常采用归一化的均方误差值进行评价[5]。

计算机图像中的噪声一般来源于对计算机图像进行获取或传输过程中受到了随机信号的干扰，从而阻碍人们对图像信息的接收。若图像噪声的信号强度和计算机图像自身的信号强度均存在不相关关系时，一般这种噪声被认为是加性噪声，而当图像噪声的信号强度和计算机图像自身的信号强度存在相关性关系时，该种噪声被认为是乘性噪声。

2　小波分解

傅里叶变换是联系频域信号和时域信号之间的桥梁，其在信号分析领域具有重要作用，若函数 满足狄利克雷条件，且

(1)

则称之为f(x)的傅里叶变换，其中f(x)是原函数，F(w)是象函数。而F(w)的傅里叶逆变换如下[6]

(2)

傅里叶变换可对某一时间段的时域信息进行分析，但无法对某一时间段所对应的频域信息或某一频率段所对应的时间信息进行分析，且傅里叶变换难以针对某时间段内的突变信号进行分析。针对以上问题，便产生了其他变换方法。小波分解在众多工程领域中均得到了广泛应用，已发展为科学技术人员普遍采用的工具之一[7]。

对此，首先产生了Gabor变换和短时傅里叶变换，其均是先对信号进行加窗处理，然后对窗内信号进行傅里叶变换，以反映信号的局部特性。但Gabor变换和短时傅里叶变换的窗函数均具有固定的大小和形状，无法对低频信号进行大时间窗分析以及对高频信号进行小时间窗分析。而小波分解却能解决这一问题，其可以保持窗函数的大小不变，但又能改变窗口的形状，实现在信号的低频区有较低的时间分辨率和较高的频率分辨率，且在信号的高频区有较低的频率分辨率和较高的时间分辨率[8-9]。

在实际应用中，由于计算机运算的特点，小波变换需要进行离散化处理之后才能在计算机上正常运行。一般定义为

(3)

式(3)为离散小波函数，则任意函数g(t)的离散小波变换DWT为

(4)

为使小波变换实现时间分辨率和频率分辨率可变化的性能，可以采用常用的二进制采样网格，由此得到二进小波，以实现对信号变焦距分析的作用[8]

(5)

式(5)为二进小波，二进小波具有可以保持时域信号平移不变量的特点，因此其可使用离散化尺度参数，而时域上的平移参量仍为连续变化。

3　Mallat算法

1989年，Mallat最先提出多分辨率分析理论，是基于将小波函数进行二进伸缩和平移来对函数进行表示的思想，通过金字塔算法进行更加抽象且复杂的方式来表示[10-11]。而小波分解在计算机图像中的应用，则必然离不开二维的Mallt算法。

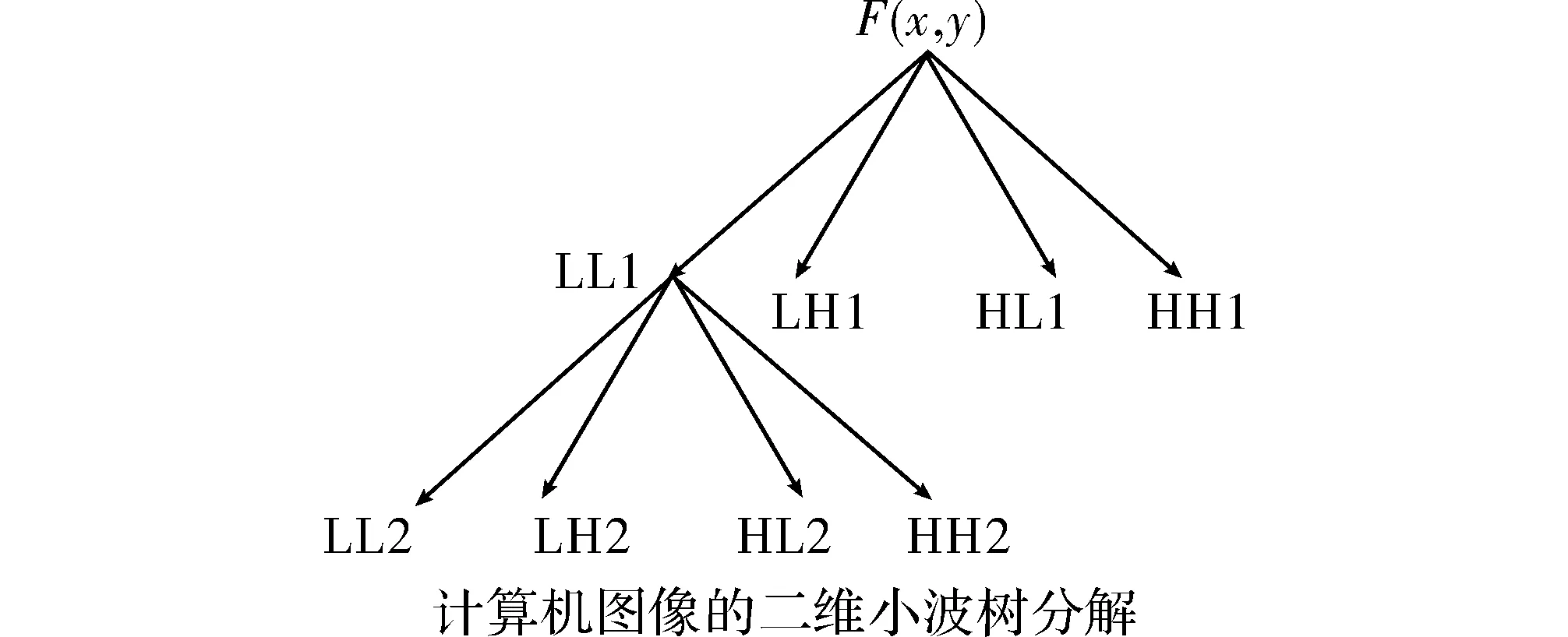
图1　图像的二维小波树分解图

如图所示为Mallat算法的图像二维小波树分解图，对于每一个图像信号F(x,y)，均可被分解为LL1、LH1、HL1和HH1共4个频带，而LL1频带上的信号还可进一步分解为LL2、LH2、HL2和HH2这4种频带的信号。依次递推，计算机图像信号可逐步进行分解。一般情况下，在LL频带上，计算机图像具有原始信息，而类HL频带上的信号反映的是计算机图像在水平方向上的变化和边缘信息，类LH频带上的信号则反映的是计算机图像在垂直方向上的变化和边缘信息，类HH频带上的信号表示的是对计算机图像信号进行高通滤波后保留下的信息[8]。

4　小波阈值去噪

与一维含噪信号去除噪声相比，计算机图像的去除噪声工作一般采取3种过程进行处理。首先，针对计算机图像，选取与之相适应的小波分解函数并选择适当的分解层数进行小波分解。然后，将小波分解后的高频系数进行小波阈值分析与处理，针对小波分解的每一层信号，选取适当的阈值对该层的水平方向、垂直方向以及斜线方向的高频系数进行阈值量化处理。阈值函数和阈值的选取与计算机图像的阈值去噪保持一致。最后，选择小波分解后的低频系数以及经过阈值量化后的高频系数针对计算机图像进行重构，从而实现对原始图像信号滤除噪声的处理工作[9]。

在图像的小波阈值去噪的过程中，阈值函数的选取一般有硬阈值函数和软阈值函数两种，如图2所示，即为硬阈值函数与软阈值函数的图像表示形式。其中，硬阈值函数是将经过小波变换后的所有系数幅值中小于阈值的系数设为零，将其去掉，再将大于阈值的小波系数进行保存且保持不变。而与硬阈值函数所不同的是，软阈值函数是用大于阈值的小波系数的绝对值减去阈值后，再将处理后的系数进行保存[10]。

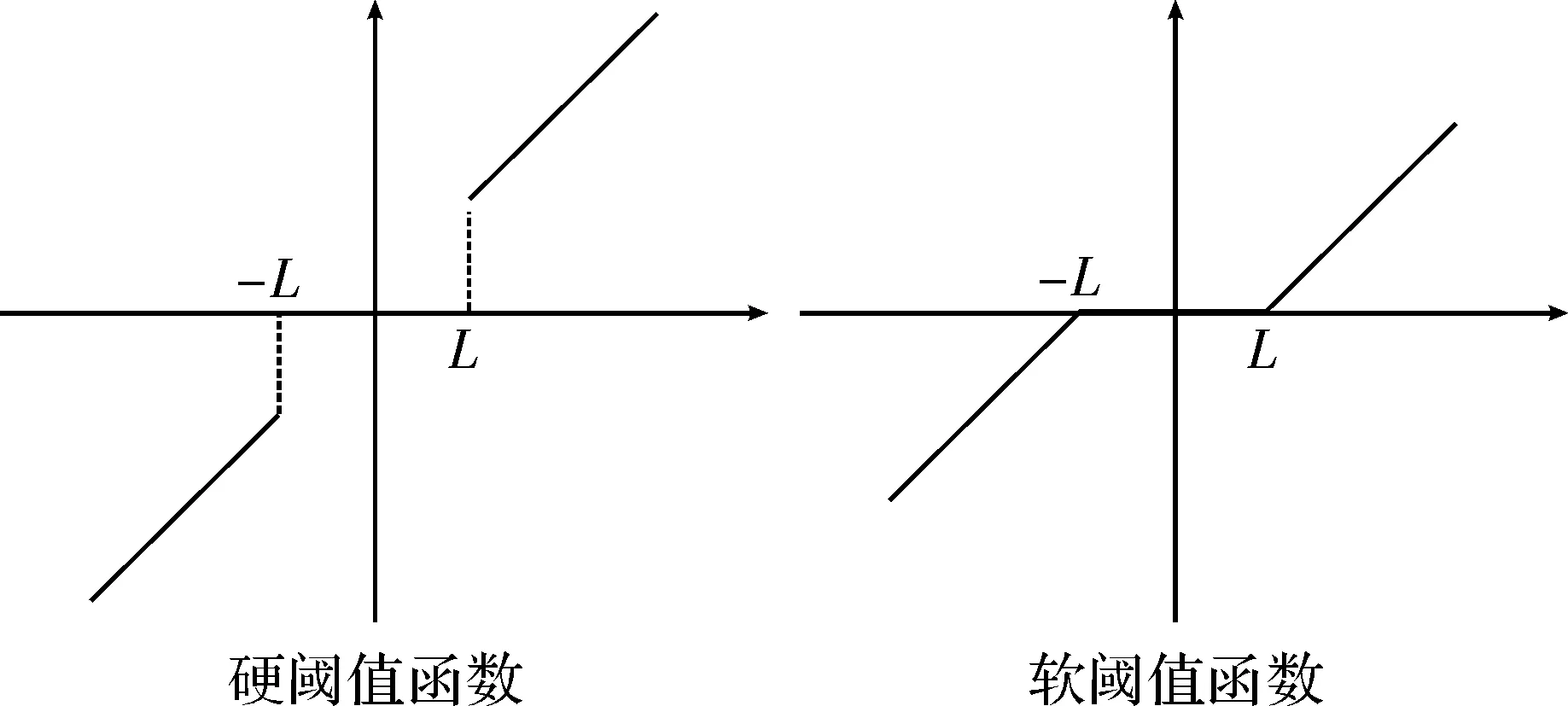
图2　软阈值函数与硬阈值函数

应用Matlab仿真软件，先对计算机图像信号进行小波分解，得到图像信号的小波分解系数，然后设定小波分解阈值，并对分解得到的小波系数中满足分解阈值的小波系数进行重构，滤除图像中的噪声，实现图像小波去噪的目的。

图3　计算机图像的小波阈值去噪

图3为图像的小波阈值去噪的实例，从图中可知，经过小波阈值去噪处理后，含有噪声的计算机图像可较好地滤除图像中的噪声，从而实现小波去噪的效果。

5　结束语

计算机图像在其信号形成的过程中易受到来自外界的干扰或仪器自身因素的影响，形成图像噪声。因此在应用计算机图像时，需要对其进行去噪处理，小波分解可对图像信号的频域进行更加细致的分解，选取适当的小波阈值，可较好地滤除图像中的噪声。经Matlab仿真，应用小波阈值方法进行图像去噪处理，能取得较好的效果。

[1]许光宇.非局部图像去噪方法及其应用研究[D].合肥:合肥工业大学,2013.

[2]张国伟.基于小波变换的图像去噪方法研究[D].昆明:昆明理工大学,2014.

[3]刘喜贵,杨万海.基于小波分解的图像融合方法及性能评价[J].自动化学报,2002,28(6):927-934.

[4]万金梁,王健.基于融合细分的纹理图像重构模型[J].计算机应用,2015,35(11):3194-3197,3202.

[5]刘斌,彭嘉雄.图像配准的小波分解方法[J].计算机辅助设计与图形学学报,2003,15(9):1070-1073.

[6]香玲,席志红.压缩感知观测矩阵的优化算法[J].电子科技,2015,28(8):102-105,111.

[7]寇为刚,谭等泰.基于EEMD和小波包分解在滚动轴承故障信息提取中的分析对比[J].工业仪表与自动化装置,2015,28(4):101-104.

[8]李玉峰.小波分析在图像去噪与压缩中的应用研究[D].长春:中国科学院长春光学精密机械与物理研究所,2005.

[9]韦力强.基于小波变换的信号去噪研究[D].长沙:湖南大学,2007.

[10] 周平,李传富,符志鹏.基于小波分解的脑CT图像纹理特征提取[J].仪器仪表学报,2010,31(3):643-648.

Computer Image Denoising Algorithm Based on Wavelet Decomposition

ZHANG Yang1, 2

(1.Renmin University of China, Beijing 100872, China;2.Department of Professional Education, Beijing Institute of Information Technology, Beijing 100070, China)

Noises arise in the formation computer images due to the interference of external factors, greatly affecting the quality of image. The image denoising can be achieved by wavelet decomposition which meticulously divides the image signals in the frequency domain and selects the appropriate threshold. This paper discusses the quality of the image, wavelet decomposition, Mallat algorithm, and the wavelet threshold denoising. The wavelet decomposition of image signal denoising is performed by Matlab simulation. The simulation results show good image denoising effect.

wavelet decomposition; image denoising; Mallat algorithm; wavelet threshold; Matlab simulation

10.16180/j.cnki.issn1007-7820.2016.08.030

2016-01-20

张洋(1979-)，女，硕士，讲师。研究方向：数字音视频技术等。

TN911.73; TP391.41

A

1007-7820(2016)08-103-03