NSGA-II在不同性能指标组合下的PID参数优化

王智浩

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海工业自动化仪表研究院，上海 200233)



NSGA-II在不同性能指标组合下的PID参数优化

王智浩1,2

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海工业自动化仪表研究院，上海 200233)

文中对于PID参数整定问题，通过分析比较不同组合的性能指标，在基于多目标智能优化算法下进行PID参数整定。该方法基于非支配排序多目标遗传算法(NSGA-II)，在采用不同性能指标组合后生成的不同目标函数空间，通过Matlab进行控制系统仿真后，对输出的阶跃响应曲线进行了分析和比较,从而寻找到了IAE、ISE以及控制输入的平方项作为最优的三目标性能指标组合。

多目标优化算法；PID; NSGA-II; Matlab

PID控制器因其算法简单、鲁棒性强,因而被广泛应用于化工、冶金、机械、热工和轻工等工业过程控制系统中[1]。但PID控制在实际运用上仍面临两个关键问题：一是建立一个综合多种因素动态数学模型通常是很困难的；另一个就是PID 参数的整定，即针对特定的系统建立数学模型，运用优化方法按照一定的性能指标进行寻优，使PID 控制系统达到所期望的控制性能。

本文旨在对第2个问题即PID参数整定提出一种新的思路和解决方法，目前最多的优化准则都是按照单一误差积分性能指标来优化系统[2]，但在实际运用中几种性能指标均有不同的优缺点，同时为了保证实际应用的效果，研究人员通常需要对准则进行修改并添加权重[3-7]。

为解决这一问题文中采用了基于非支配排序多目标遗传算法(Non-dominated Sorting Genetic Algorithm II ，NSGA-II)[8]，算法是目前流行的多目标进化算法之一。该算法已在类似的多目标优化问题上取得了较好的效果[9-10]，其在使用中最大的优势在于无需考虑权重的问题，该算法可对多个目标进行综合比较从而取得Pareto最优(即最优的PID参数集合)，这在较大程度上保留了不同性能指标的优点同时也消除了彼此的缺点。

1　基于NSGA-II的PID参数优化设计

1.1基于NSGA-II的PID控制系统原理

控制系统由控制器和被控对象以及优化设计环节组成，控制系统框图如图1所示。

图1　控制系统框图

在该控制系统中由控制器根据设定值r与实际输出值y进行比较，所得偏差e作为PID 控制器的输入值，经PID控制产生控制量u(k)，之后将所得偏差e(k)、控制量u(k)与实际输出值Yout(t)输入优化设计模块。利用NSGA-II算法对PID控制器的比例增益Kp、积分增益Ki、微分增益Kd这3个参数组合在一起作为进化算法种群中的个体即决策变量，以几种误差积分性能指标组合来为目标函数空间，并以其可能达到的极小值作为评价指标。然后对种群个体进行选择、排序、交叉和变异操作，不断地进化，直到找到群体中最优目标个体，得到PID 控制器的最优参数，使系统的稳定性、快速性、准确性整体综合性能达到理想的控制效果。

1.2PID控制原理

PID控制器是一种线性控制器，其是将偏差e(t)的比例、积分和微分通过线性组合构成控制量对被控对象进行控制。式(1)为其控制规律，式(2)为修改后的方程

(1)

(2)

式中，t为时间；kp表示比例增益；u(t)为本次控制量；e(t)为本次偏差；Ti表示积分时间常数；Td表示微分时间常数；ki表示积分增益；kd表示微分增益；ki=kp/Ti，kd=kp×Td。

为仿真方便，可通过离散化将连续系统直接化为差分方程。式(2)即为离散化后的差分方程

Δu(t)=Kpe(t)+KiΔe(t)+KaΔ2e(t)

(3)

1.3性能指标

这里文献[11]选取了6种误差积分准则的性能指标，如表1所示。

表1　6种性能指标函数数字算法

1.4算法流程

基于非支配排序多目标遗传算法(NSGA-II)的执行步骤如下：(1)初始化种群。等概率初始化每个个体的纯变异策略；(2)排序。按照性能指标组成的目标函数进行非支配排序确定非支配序列，进而对每个个体进行适应度计算；(3)混合变异操作。根据个体变异的概率，产生子代个体；(4)选择。选取父代种群以及子代种群的集合，利用锦标赛方法(即首先比较排序，若处于相同序列，则进行拥挤度算子比较)选择出下一代种群个体；(5)终止。判断是否满足最大演化代数的终止，若满足，则算法终止；否则重复步骤(2)～步骤(4)，直至满足终止条件。

2　实验仿真

2.1实验对象及参数选取

在过程控制中，许多系统在进行系统辨识时常被近似为一阶或二阶的典型系统，为比较NSGA-II算法用在PID控制器参数优化整定的性能，针对以下二阶时滞对象进行仿真研究,并与相同性能指标的SOA算法以及PSO算法进行比较。选取被控对象其传递函数为

(4)

其中，参数Kp、Ki、Kd的范围分别为[0, 100]、[0, 100]和[0, 100], 输入信号为单位阶跃响应。群体大小为100,终止代数为100, 控制器的输出限值为[-10, 10]。交叉概率0.9，变异率0.5，采用实数编码。

2.2适应度函数选取

对于PSO和SOA算法，为获得满意的过度过程动态性能，采用IAE性能指标作为参数选择的最小目标函数。同时为防止控制能量过大，在目标函数中加入控制输入的平方项，选用的目标函数如式(5)所示。

(5)

其中，u(t)为本次控制量；e(t)为本次偏差；ω1和ω1为权值。

为避免超调，采用了惩罚控制，如果e(t)<0，则超调量将作为最优指标的一项，此时目标函数如式(6)所示。

(6)

其中，ω3为权值，且ω3≥ω1，这里取ω1=0.999，ω2=0.001,ω3=100。

对于NSGA-II算法，文中在保留惩罚控制的前提下，取消了上述权重ω1和ω2，并将式(5)和式(6)重修改为对应的目标函数，此时目标函数为式(7)～式(9)

(7)

(8)

(9)

其中，式(6)和式(8)为惩罚控制，当且仅当e(t)<0时才会选用这个方程，一般情况只使用式(5)和式(7)。

2.3仿真结果与分析

图2为NSGA-II算法种群分布，说明F1和F2是两个相互冲突的目标函数，且其中的曲线正是NSGA-II算法所寻找到的Pareto最优前端。图3显示了各算法在PID控制的阶跃响应效果，可从图中看到NSGA-II算法相较于其他算法在响应时间上取得了较好的效果，且并未产生过大的超调量。

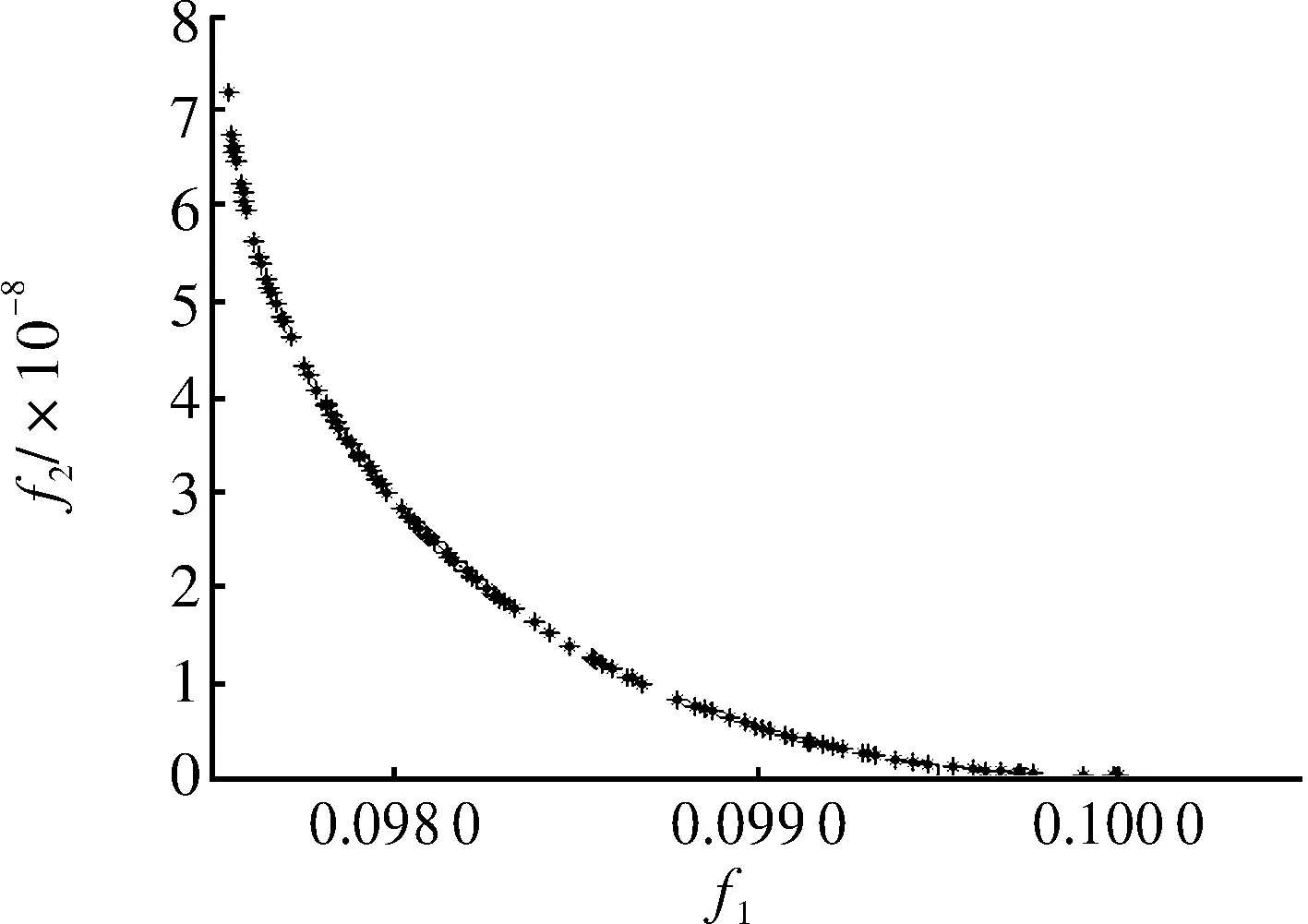
图2　种群分布

图3　阶跃响应输出曲线比较

此外，由于NSGA-II算法是个多目标优化算法，该算法可对多个目标函数进行计算，并可通过添加额外的性能指标来取得更好的Pareto最优解，即PID参数。之前通过IAE性能指标来构造二维目标函数空间，之后可通过分别添加误差平方项的性能指标如ISTSE、ITSE、ISE来构造三维目标函数空间(添加的性能指标的目标函数作为F2，式(9)变为F3)。如图4～图7是通过添加性能指标后的种群分布及相应的PID控制的阶跃响应效果图。

图4　添加ISE后的种群分布

图5　添加ITSE后的种群分布

图6　添加ISTSE后的种群分布

图7　阶跃响应输出曲线综合比较

通过对比图4～图6后可发现，虽不同的F2对种群的分布产生了一定影响，但种群在F1和F2的面上并未产生较大的改变，说明添加误差平方项的性能指标后的阶跃响应输出曲线，相较于双目标函数的曲线，在添加后的三目标函数输出的曲线在此有了更进一步的优化，但不同的误差平方项对结果没有过大影响。同样在图7中综合比较所有的三目标函数结果后，说明虽三目标相对于双目标有了进一步的优化，但误差平方项与时间的乘积并未产生较大的影响。由此说明，影响Pareto最优解的主要因素是误差平方项即ISE。因此，为减少算法的运行时间，选用目标函数组合IAE和ISE以及控制输入的平方项作为最优组合。

3　结束语

文中提出了利用非支配排序多目标遗传算法(NSGA-II)，基于误差积分准则的性能指标和控制输入的平方项对PID进行参数优化。与其他算法相比，取消了除惩罚参数之外的所有需要人工进行干预的权重参数的选择及输入，消除了因权重不同可能引起的不同优化结果，使所有的PID参数优化结果无需进行额外的经验，而只需选取相应的性能指标即IAE和ISE。通过仿真试验对此方法进行验证，优化获得的增益参数应用于PID控制器中达到了良好的控制性能，如超调小、调节时间短、上升时间快、稳态误差小等等，结果表明此方法的有效性和实用性。

[1]胡包钢,应浩.模糊PID控制技术研究发展回顾及其面临的若干重要问题[J].自动化学报,2001,27(4):567-584.

[2]金翠云,王建林,马江宁,等.改进的PSO算法及其在PID控制器参数整定中的应用[J]. 电子测量与仪器学报,2010,24(2):141-146.

[3]曾自力.基于进化算法的PID控制系统设计方法研究[D].南京:南京理工大学,2006.

[4]楚东来.基于改进粒子群算法的自抗扰控制器参数优化及仿真[J].信息通信,2015(9):15-17.

[5]李自强,薛美盛.用于PID参数自整定的性能指标仿真研究[J]. 自动化与仪表,2009(2):30-33.

[6]张倩,杨耀权.基于遗传算法的PID控制器参数优化方法研究[J].电力科学与工程,2011,27(11):53-57.

[7]郑权,忻尚芝,钱建秋.基于改进遗传算法的PID参数研究[J].电子科技,2015,28(11):5-7,12.

[8]Deb K,Pratap A,Argrawal S, et al.A fast and elitist multi-objective genetic algorithm:NSGA II[J].IEEE Transactions on Evolutionary Computation,2002, 6(2):182-197.

[9]王洪建.基于NSGA-Ⅱ的变速器齿轮系多目标可靠性优化设计[D].武汉:武汉理工大学,2010.

[10] 颜伏伍,王洪建,田韶鹏,等.基于第二代非支配排序遗传算法的变速器齿轮系多目标可靠性优化[J].汽车工程,2010,32(3):234-237.

[11] 阳国富.几种最佳性能指标下的PID参数寻优[J].云南工学院学报,1991,7(3):68-72.

Research on PID Parameters Based on NSGA-II in a Combination of Different Indicators

WANG Zhihao1, 2

(1.School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2.Shanghai Institute of Process Automation Instrumentation, Shanghai 200233, China)

The PID parameter optimization based on multi-objective evolutionary algorithm is proposed by analyzing performance metrics to compare different combinations. The method is based on the non-dominated sorting genetic algorithm II (NSGA-II) for generating different targets after the introduction of different indicators combination of properties function. Analysis and comparison the curves of step response output is made through Matlab simulation of the control system to find the optimal combination of the performance indicators IAE, ISE and squared term control input.

multi-objective evolutionary algorithm; PID; NSGA-II; Matlab

10.16180/j.cnki.issn1007-7820.2016.08.021

2015-11-22

王智浩(1991-)，男，硕士研究生。研究方向：智能算法。

TP301.6

A

1007-7820(2016)08-070-04