时频分析在雷达信号识别中的应用

杨宏飞，何正日

(西安电子科技大学 电子工程学院，陕西 西安 710071)



时频分析在雷达信号识别中的应用

杨宏飞，何正日

(西安电子科技大学 电子工程学院，陕西 西安 710071)

针对目前雷达信号分选识别的问题，研究了时频分析的方法在信号识别方面的应用。该方法与其他雷达信号识别方法相比，能有效地分析非平稳信号。在时频分析相关理论的基础上，分别研究了基于短时傅里叶(STFT)变换和Wigner-Ville分布(WVD)方法对信号特征的分析和提取。通过仿真，分析对比了两种方法的优劣性, STFT可分析出信号的局部频域特性，而相同信噪比下, WVD比STFT受噪声影响小、聚合度高，能更好地体现时间和频率之间的关系，由此表明，两种方法均可较好地区分出调制信号特征。

时频分析；短时傅里叶；Wigner-Ville分布

雷达辐射源信号识别在现代电子支援侦察(ESM)和电子情报侦察(ELINT)任务中发挥着重要作用，是电子对抗领域研究的重要课题[1]。

当前，战场电磁环境日趋复杂，雷达信号的脉内特征相比传统的雷达参数具有较好的稳定性和可靠性，能够较好地满足现代雷达信号识别的要求[2-3]。时频分析反映了信号的时变规律，是分析时变非平稳信号的有力工具，其作为一种新兴的信号处理方法已成为当前信号处理研究的热点，也是雷达信号识别的重要方法。在许多文献中，已使用时频分析方法对信号脉内特征进行提取，来实现对雷达信号的识别。例如：文献[4]采用时频综合分析法对相位编码和线性调频雷达辐射源信号进行了特征分析；文献[5]将WVD用于对雷达回波的分类；文献[6]通过时频分析的方法提取线性和双曲线调制Chirp信号的脉内调制特征；文献[7]利用WVD和正交镜像滤波器(QMF)对调频连续波(FMCW)和P4码雷达信号进行识别，在中等信噪比条件下具有较佳的识别性能；文献[8]运用时频分析方法对FM信号进行估计和分类；文献[9～10]基于时频分析方法，提出了一种的具有脉内特征分析能力的数字信道化接收机方案；文献[11]提出一种雷达辐射源信号时频原子特征分析方法，构建了辐射源信号分解的过完备原子库，对信号进行时频原子分解，得到表征信号特征信息的最匹配时频原子特征；文献[13]提取了雷达信号的WVD且将其简化到二维(2D)，之后再利用小波变换的方法进行不同雷达信号的识别。以上方法主要运用时频分析方法对信号脉内特征进行了分析，实现了多种信号的分类识别，其信号识别的准确率以及抗噪声性能还有待进一步提高。

在此基础上，本文将对时频分析中的STFT和WVD方法在雷达辐射源信号识别中的应用进行重点研究。

1　STFT在信号识别中的应用

STFT是一种最常见的时频分析方法，其实质就是加窗的FT(Fourier Transform)。其基本思想是通过滑动窗将非平稳信号截取为多个子段，然后再对每一段信号都做傅里叶变换处理，由此便可分析出在间隔时间段内存在的频率。

设有一信号表示为x(t)，其STFT的定义为

(3)

STFT变换具有线性叠加性。

设x(t)=ax1(t)+bx2(t)，记x(t)，x1(t)和x2(t)的STFT表示分别为p(t,f)，p1(t,f)，p2(t,f)则有

p(t,f)=ap1(t,f)+bp2(t,f)

(4)

因对其进行加窗的操作会直接影响其频率的分辨率，所以为保证能从短时傅里叶中恢复出原信号，窗函数就必须符合一定的限制条件。常用的窗函数有Hamming窗和Gaussian窗等[10]。由于STFT的运算复杂度小，且某种程度上能够体现出信号的细节特性，因而，其在信号处理方面的应用非常重要。然而由于STFT的窗函数决定了频率和时间的分辨率，而其分辨率又无法同时达到最佳效果。尽管如此，STFT仍不乏为一种有用的时间频率分析手段。

以下就常用雷达信号对其进行STFT仿真。对采样率为60 MHz，调频带宽为15 MHz，脉宽为4 μs，起始频率置为10 MHz的LFM信号和对采样率为60 MHz，载波频率为10 MHz，码元宽度为0.5 μs的BPSK信号分别进行STFT，窗宽设置为64，同时在信号上加信噪比为15 dB的白噪声。

由仿真图1～图3可明显看出，不同调制信号特征之间的差异。LFM信号频率随时间成线性变化，BPSK信号的频率不随着时间推移而发生改变，而FSK可看出来有两个频率值。通过等高线仿真图可以直观地区别出不同调制信号间的差异，与经典方式相比，可看出这种方法具有良好的抗噪能力。然而从图中可知，这种方法也仅能简单表现出频率与时间之间的关系，无法更细致地得到信号特征。

图1　LFM信号经过STFT后的时频图

图2　BPSK信号经过STFT后的时频图

图3　FSK信号经过STFT后的时频图

2　Wigner-Ville分布在信号识别应用

WVD是一种能反应出信号的能量密度的时频表示方式，其以频率ω及时间t为变量，假设有一个信号x(t)则其WVD为

(5)

WVD主要有以下几种性质：(1)实性。即WVD分布始终是实数;(2)对称性。Wx(t,ω)=Wx(t,-ω),Wx(t,ω)=Wx(-t,ω);(3)时间和频率的边缘特性;(4)时间和频率的位移特性。即若s(t)→ejω0ts(t-t0)，则有Wx(t,ω)→Wx(t-t0,ω-ω0)。

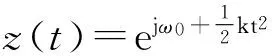
exp[j(ω0+kt)τ]

(6)

由此可求得其WVD分布为

(7)

这里使用了积分结果

(8)

从式(7)中可看出，LFM信号的WVD是沿ω=ω0+kt分布的冲激谱，也就是说LFM信号的WVD的幅值是聚拢在表示该信号的瞬间频率的改变率的线的周围的。所以，可以看出，LFM信号的WVD分布是拥有较好的时频聚拢特性。

假设LFM信号的参数设置为：采样率60 MHz，调频带宽15 MHz，起始频率10 MHz，脉宽4 μs，并分别加入15 dB和2 dB的噪声，则其经过WVD后的等高线仿真结果如图4所示。

从图4(a)和图4(b)可知，在WVD中信号时频的聚拢线并不随噪声的改变而呈现出较大的变化。且由图1和图4(a)可知，在相同信噪比的条件下，WVD比STFT受噪声影响程度更小，聚合度更高，且WVD分布比STFT能更好地表现出时间同频率之间的联系。

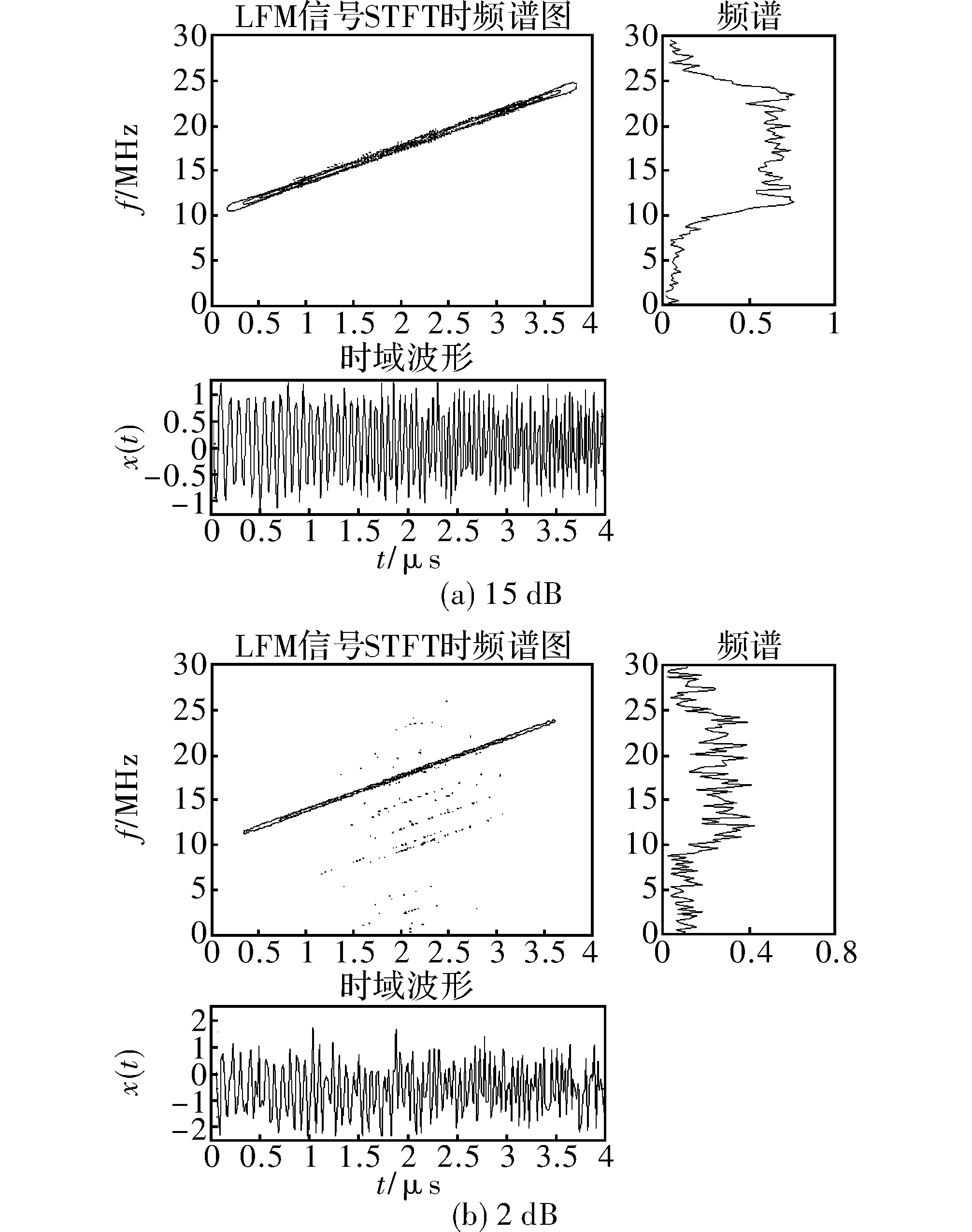
图4　LFM加入白噪声后WVD分布的时频图

若在前面的LFM信号上再增加一条LFM信号，并将其信号参数设置为：起始频率0 MHz，采样率60 MHz，脉宽4 μs，带宽15 MHz。加入15 dB的白噪声，对其进行仿真，得到结果如图5所示。

从图5中可直接地区分出两个LFM信号的时频特性，然而在这两条分布线之间还出现了一个干扰线，文中将其称为交叉干扰，对于交叉干扰的抑制本文不做讨论。

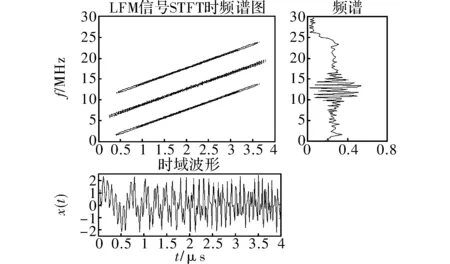
图5　两个LFM信号的WVD时频图

总而言之，STFT以及WVD分布可较好地区分出调制信号的特征，但其也有各自不同的优缺点。比如：STFT可分析出信号的局部频域特性，但不能同时兼顾到频率和时间的分辨；而WVD虽频率分辨率比STFT高，但有交叉干扰的存在，且当采样点数较多时，其计算时间也将有较大的延长。

3　结束语

本文在时频分析的相关理论的基础上，对其应用方法进行分析和讨论，研究了其在辐射源信号特征提取方面的应用。然后重点对通过STFT和WVD方法在信号的识别方面的应用做了详细的研究和分析，并用这两种时间频率分析方法对常见的雷达信号进行了仿真验证，通过STFT的仿真，说明了STFT对LFM，BPSK和BFSK较好的识别效果，用WVD则通过仿真可明显看出其对信号的频率分辨率能力比STFT强，然而通过WVD分布后，会有交叉干扰存在，且当采样点数过多时，其计算花费的时间也将大幅增长。

[1]陈慧玲.信号个体特征的检测和识别技术研究[D]. 西安:西安电子科技大学,2013.

[2]Yi W.A novel method for sorting unknown radar emitter[J].Microcom-puter Information,2010,4(1):85 -86.

[3]Zhixiang Y, Zhu Y Q, Xiaoning L,et al. Sorting radar emitter signal based on wpt6 and cr1[C]. Tianjin: 2009 2nd International Congress on Image and Signal Processing, CISP’09, 2009.

[4]阎向东,张庆荣.脉压信号脉内调制特征提取[J].电子对抗,1991(4):23-32.

[5]Kumar P K,Prabhu K M.Classification of radar returns using Wigner-Ville distribution[C].KL,USA: Proceedings of International Conference on Acoustics, Speech,and Signal Processing,1996.

[6]Moraitakis I,Fargues M P.Feature extraction of intra-pulse modulated signals using time-frequency analysis[C].NM,USA: Proceedings of 21st Century Military Communications Conference,2000.

[7]Milne P R,Pace P E.Wigner distribution and analysis of FMCW and P-4 polyphase LPI waveforms[C].Orlando,EL: IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP’02),2002.

[8]Christophe De Luigi,Claude Jauffret.Estimation and classification of FM signals using time-frequency transforms[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(2):421-437.

[9]Gustavo L R,Jesus G,Alvora S O.Digital channelized receiver based on time-frequency analysis for signal interception[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(3): 879-898.

[10] Gustavo L R,Jesus G. Multiple signal detection and estimation using atomic decomposition and EM[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):84-102.

[11] 朱明,金炜东,普运伟,等.基于Chirplet原子的雷达辐射源信号特征提取[J].红外与毫米波学报,2007,26(4):302-306.

[12] Huadong L,Jianghong H.Sorting radar signal based on wavelet characteristics of wigner-ville distribution[J].Journal of Electronics(China),2013, 5(2): 1-5.

Time-frequency Analysis in Radar Signal Recognition

YANG Hongfei, HE Zhengri

(School of Electronic Engineering, Xidian University, Xi’an 710071, China)

The application of frequency analysis in signal recognition for sorting radar signal is discussed. This method offers better efficiency in the analysis of non-stationary signals than other radar signal recognition method. Signal feature extraction by the short-time Fourier analysis (STFT) transformation and the Wigner-Ville Distribution (WVD) is studied respectively and compared by simulation, which shows that STFT can analyze partial frequency domain characteristics of the signal, while at the same SNR, WVD enjoys a smaller noise ratio and a higher degree of polymerization, hence better reflecting the relationship between time and frequency; both methods are able to distinguish the characteristics of modulated signals.

time-frequency analysis; short time Fourier; Wigner-Ville distribution

10.16180/j.cnki.issn1007-7820.2016.08.017

2015-11-24

杨宏飞(1985-)，男，硕士研究生。研究方向：电子对抗。何正日(1990-)，男，硕士研究生。研究方向：电子对抗。

TN97

A

1007-7820(2016)08-058-04