星载BDS/GPS低轨卫星自主定轨精度分析

熊　超，贾小林，朱　俊，卢传芳

(1.西安航天天绘数据技术有限公司，陕西　西安　710100；2.地理信息工程国家重点实验室，陕西　西安　710054；3.西安测绘研究所，陕西　西安　710054；4.宇航动力学国家重点实验室，陕西　西安　710043；5.中国西安卫星测控中心，陕西　西安　710043)



星载BDS/GPS低轨卫星自主定轨精度分析

熊超1，贾小林2，3，朱俊4，5，卢传芳1

(1.西安航天天绘数据技术有限公司，陕西西安710100；2.地理信息工程国家重点实验室，陕西西安710054；3.西安测绘研究所，陕西西安710054；4.宇航动力学国家重点实验室，陕西西安710043；5.中国西安卫星测控中心，陕西西安710043)

为了进一步研究低轨卫星搭载BDS/GPS接收机实现自主定轨的热点问题，讨论了基于星载BDS/GPS自主定轨需要考虑的数学模型，提出了顾及动力学模型的Helmert方差分量估计实现基于星载BDS/GPS自主定轨的方法，并阐述了方法的原理及自主定轨的过程；然后基于自主研发程序，利用高动态信号仿真器仿真的星载BDS/GPS数据验证了基于星载BDS/GPS自主定轨的可行性及其能达到的精度。结果表明，顾及动力学模型的Helmert方差分量估计既可以较好地解决BDS/GPS观测值的合理定权问题，又可以有效地减弱粗差的影响，提高定轨精度。

自主定轨；扩展卡尔曼滤波；方差分量估计

0　引言

北斗卫星导航系统(BeiDou navigation satellite system，BDS)是我国自主研发、独立运行的全球卫星导航系统。其空间星座由5条地球静止轨道(geostationary Earth orbit，GEO)卫星、27条中圆地球轨道(medium Earth orbit，MEO)卫星和3条倾斜地球同步轨道(inclined geosynchronous satellite orbit，IGSO)卫星组成。截止到2012年底，在轨工作卫星有5颗GEO卫星、4颗MEO卫星和5颗IGSO卫星共计14颗卫星，已具备区域服务能力[1]。

长期以来，基于卫星导航系统的低轨卫星高精度定轨主要依靠全球定位系统(global positioning system，GPS)，围绕各种不同需求，低轨卫星的星载GPS定轨技术取得了迅速发展。首次用星载GPS测量获得cm级定轨精度的成功范例是TOPEX/POSEIDON海洋测高卫星(简称为T/P卫星)。美国航空航天局(National Aeronautics and Space Administration，NASA)下属的喷气推进实验室(Jet Propulsion Laboratory，JPL)用星载GPS测量数据作精密定轨数据处理，结果表明：T/P卫星径向轨道精度达到3 cm，切向和法向的轨道精度优于10 cm。星载GPS测量在卫星精密定轨方面取得巨大成功的同时，世界各国也在积极开展自主定轨的研究和试验工作。JPL在其研制的高精度定位定轨软件GIPSY的基础上，研制出一套实时版GIPSY软件(real-time GIPSY，RTG)[2]。该软件不仅可用于低轨卫星的自主定轨，也可用于地面飞机的实时定位。用T/P卫星实测数据验证表明，在有选择可用性(selective availability，SA) 的影响下，经过约4 h的滤波收敛时间后，3维数据求得的实时定轨轨道均方根(root mean square，RMS)为3～5 m。文献[3]将RTG软件用于SAC-C卫星的自主定轨，结果表明：自主定轨精度可达到1.5 m。文献[4]于2006年研制成功了星载GPS自主定轨软件SATODS，并用大量的星载GPS实测数据进行模拟自主定轨的试验，试验结果表明：自主定轨精度可以达到±1.5～3.0 m轨道精度和±3 mm/s的速度精度[4]。

低轨卫星及星座作为高精度对地观测系统的传感器搭载平台，已广泛应用于资源遥感、大气探测、海洋开发、军事侦察等领域，在科学研究、经济建设、社会发展及国家安全中具有不可替代的作用。作为我国新一代自主导航系统，BDS区域导航系统的建成将改变我国对GPS依赖的局面提供可能；同时BDS/GPS组合卫星导航系统可以使可视卫星数显著增加，并改善卫星的几何分布结构，提高系统的可用性和可靠性[1]；因此低轨卫星搭载BDS/GPS接收机实现自主定轨将成为定轨领域的热点问题。

本文研究讨论基于星载BDS/GPS自主定轨相关问题，并实验验证基于星载BDS/GPS自主定轨的可行性及其能达到的精度。

1　数据处理策略

1.1数据处理

1.1.1状态方程和观测方程

星载BDS/GPS自主定轨是根据带有随机误差的一系列观测信息和卫星轨道的动力学信息，依照一定的准则，对卫星运行状态参数、动力学模型参数、观测模型参数等进行最优估计的过程。自主定轨常以序贯或者递推方式进行数据处理和参数估计，一般采用扩展卡尔曼滤波(extended Kalman filter，EKF)估计方法[4-5]。建立星载BDS和GPS自主定轨的数学模型，必须建立自主定轨扩展卡尔曼滤波的状态方程和观测方程。

对于低轨卫星来说，大气阻力和太阳光压这2种非保守力对卫星轨道影响较大，同时又是难以精确模型化的摄动力，在动力学定轨时常将大气阻力系数CD和太阳光压系数CR作为状态参数进行估计[6-8]。相比于单一导航卫星系统，由于不同导航系统间信号延迟的存在，在观测方程中需顾及BDS/GPS系统间信号延迟，一般采用GPS接收机钟差作为基准，将BDS接收机钟差表达成GPS接收机钟差的形式。因此自主定轨系统状态向量确定为

(1)

采用消电离层伪距非差线性组合PC观测值，同时顾及BDS/GPS的系统时间偏差δtG-C，其观测方程可表示为：

(2)

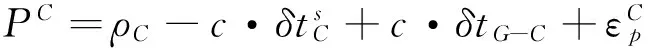
(3)

(5)

对于BDS卫星可表示为

(6)

1.1.2观测模型和动力学模型

本文在自主定轨时，处理的是消电离层伪距非差线性组合PC观测值。表1给出了具体的观测模型。

对于低轨卫星来说，大气阻力和太阳光压这2种非保守力对卫星轨道影响较大，同时又是难以精确模型化的摄动力。在动力学定轨时常将大气阻力系数和太阳光压系数作为状态参数进行估计。详细的动力学模型见表2。

表1　观测模型和估计参数

表2　动力学模型和估计参数

1.2定权策略

由于BDS星座的分布、频率特征、轨道精度、观测数据质量等方面和GPS等都存在差别，如何对观测资料进行合理加权是星载BDS和GPS自主定轨中的一个重要问题。在实际定轨过程中，观测资料有3种途径定权：1)利用观测文件中提供的标准偏差；2)根据经验定权；3)利用方差分量估计。由于观测数据文件中观测值的标准偏差只代表观测的内符合情况，而经验加权法也不能很好地反映观测资料的实际精度，低轨卫星不断运动造成随机噪声改变进而影响固定权比，会导致自主定轨精度下降。Helmert方差分量估计是一种通过迭代计算自适应确定不同类观测值权比的验后方差分量估计方法，能够在计算过程中自动地调整不同类观测值的权比，合理分配不同类观测值对整个解的贡献大小；因而在数据处理领域得到了广泛的应用。数据处理过程中，观测信息难免有粗差以及轨道预报值难免有异常，为减弱粗差和轨道预报值异常对自主定轨结果的影响，采用顾及动力学模型的Helmert方差分量估计方法[9]对仿真数据进行星载BDS/GPS自主定轨实验。

首先可构造极值条件为

(7)

(8)

然后顾及动力学模型信息，采用自适应估计原理[10]，其原理为

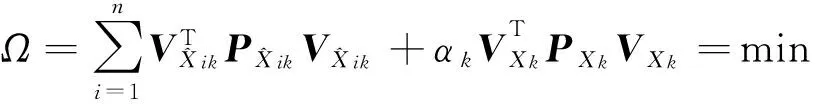
(9)

则自适应融合解为：

(10)

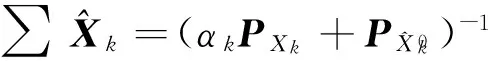
(11)

(12)

2　实验与结果分析

2.1数据准备及处理流程

目前尚无法获取星载BDS/GPS接收机实测数据，本文通过模拟数据来进行试验，试验数据是由高动态信号仿真器产生。高动态信号仿真器根据BDS和GPS卫星的精密轨道和钟差以及在轨卫星的运动轨迹，模拟产生射频信号。接收机通过接收模拟射频信号获取各卫星的观测值。

自主定轨仿真验证软件通过解算接收机的观测值得到自主定轨结果，定轨结果与仿真器输出的卫星轨道比较可以综合分析利用低轨卫星高动态BDS/GPS接收机的自主定轨能力。图1是星载BDS/GPS自主定轨仿真验证的流程图。

本文使用的试验数据为：2014-09-05的BDS精密星历和钟差、2014-09-05的GPS精密星历和钟差。数据来源为由地球科学研究中心(DeutschesGeoForschungsZentrum，GFZ)提供的BDS和GPS双系统的轨道钟差产品，文件名为gbm18085.sp3和gbm18085.clk。广播星历采用包含BDS和GPS的多系统混合的广播星历产品，文件名为brdm2480.14p。观测数据采用由高动态信号仿真器生成的2014-09-05的BDS/GPS仿真观测数据。

本文以重力反演与气候实验卫星(gravityrecoveryandclimateexperiment，GRACE)为背景模拟1颗具有星载BDS/GPS接收机的低轨卫星GRACE-A。GRACE-A轨道真值取JPL提供的GRACE-A精密轨道。本文采用2014-09-05全天24h的星载BDS/GPS模拟观测数据进行数据处理。

2.2不同定权策略的自主定轨精度分析

由于BDS与GPS的卫星星历精度不同，观测数据噪声也不同，为分析这些不同对BDS/GPS自主定轨结果的影响，在试验中分别对BDS和GPS进行不同定权策略的自主定轨。经验定权采用BDS和GPS按照1:3的权比来定权。采用2014-09-05的BDS/GPS仿真观测数据采用不同定权策略进行BDS/GPS自主定轨精度分析。

采用上述仿真数据，按照以下方案进行数据处理，测试不同定权策略的联合自主定轨的精度及其性能。数据处理方案包括：1)方案1，经验定权的自主定轨的精度分析；2)方案2，Helmert方差分量估计的自主定轨的精度分析；3)方案3，顾及动力学模型的Helmert方差分量估计的自主定轨的精度分析。不同策略的定轨结果如图2所示。

图2　不同定权策略BDS/GPS自主定轨结果

方案1和方案2不考虑动力学模型。从图2可以看出，采用经验定权方法进行自主定轨波动较大，径向、切向和法向方向均呈现明显的“尖刺”状。采用Helmert方差分量估计后，误差曲线较之经验定权平缓些，这是因为Helmert方差分量估计合理调整了BDS和GPS观测信息的权比，保证了BDS和GPS观测信息在联合自主定轨中的合理贡献；但从图2中可以看出，误差曲线仍然存在部分“尖刺”状。对于星载高动态观测数据来说，观测信息存在粗差不可避免，存在部分异常观测数据，导致估计的方差分量不可靠。而采用顾及动力学模型的Helmert方差分量估计，误差曲线比采用Helmert方差分量估计的误差曲线更为平缓；不仅合理地分配了BDS和GPS观测信息在自主定轨中的贡献，而且自适应地合理利用了动力学模型信息，联合自主定轨结果误差曲线平稳。

为了进一步分析不同定权策略对BDS/GPS联合自主定轨结果的影响，我们对3种方案进行了位置和速度的径向、切向、法向和3维定轨结果的RMS统计，具体详见表3和表4。

表3　不同定权策略BDS/GPS自主定轨位置结果　m

表4　不同定权策略BDS/GPS自主定轨速度结果　mm·s-1

从表3和表4的位置和速度结果表明：Helmert方差分量估计自主定轨位置结果比经验定权法在径向、切向、法向和3维方向提高了0.66、0.75、0.91和1.34 m；顾及动力学模型的Helmert方差分量估计自主定轨位置结果比Helmert方差分量估计自主定轨结果各方向分别提高了0.27、0.04、0.11和0.25 m；对于速度结果来说，Helmert方差分量估计和顾及动力学模型的Helmert方差分量估计相比经验定权法在切向、法向方向改善较大，主要是因为BDS卫星目前主要分布在亚太地区，部分区域观测信息质量较差，采用方差分量估计方法可以提高GPS观测信息在联合自主定轨的贡献；顾及动力学模型的Helmert方差分量估计自主定轨位置3维RMS为1.188 m，速度3维RMS为2.345 mm/s。表3和表4表明顾及动力学模型的Helmert方差分量估计既较好地解决了BDS/GPS观测值的合理定权问题，又有效地减弱了粗差的影响，从而提高了定轨精度。

2.3BDS、GPS和BDS/GPS自主定轨精度分析

BDS的区域系统空间部分由5颗GEO卫星、5颗IGSO卫星和4颗MEO卫星星座构成，其中5颗GEO卫星分别定点于58.75°E、80°E、110.5°E、140°E、160°E；5颗IGSO卫星分布于3个轨道面上，其中I1、I2和I3星下点轨迹重合，交点地理经度处于118°E，I5和I6分别和I1、I2处于同一轨道面，与I1、I2各自相差23°，交点地理经度处于95°E；4颗MEO卫星轨道高度21 528 km，为7 d 13圈回归，4颗卫星分别位于WALKER24/3/1星座的第一和第二轨道面上，星下点轨迹见图3。

图3　BDS区域卫星导航系统(5GEO/5IGSO/4MEO)星下点轨迹

为了评价BDS/GPS联合自主定轨的性能，通常可以将BDS/GPS联合自主定轨的结果与BDS、GPS自主定轨的结果进行比较分析。采用2014-09-05的BDS/GPS仿真观测数据进行GPS、BDS和BDS/GPS自主定轨精度分析。

采用上述仿真数据，按照以下方案进行数据处理，测试联合自主定轨的精度及其性能。数据处理方案包括：1)方案1，GPS自主定轨的精度分析；2)方案2，BD2自主定轨的精度分析；3)方案3，GPS/BD2联合自主定轨的精度分析。

统计试验数据的可见卫星数如图4所示。GPS可见卫星数为7～11颗；BDS可见卫星数为3～7颗；BDS和GPS联合可见卫星数为12～16颗。加入BDS后历元可见卫星数增加了5颗左右。

图5为试验数据BDS、GPS和BDS/GPS的位置精度衰减因子(position dilution of precision，PDOP)值统计图。

图4　可见卫星数

图5　PDOP统计

由图5可以看出，GPS和BDS/GPS的PDOP值相差很小，均值分别为0.87和0.82，GPS加入BDS后，PDOP减小了0.05；而BDS的PDOP值则出现较大波动，均值为4.96，主要是因为BDS为区域系统，卫星主要分布在亚太区域(见图3)，当低轨卫星运行到覆盖区域内，可以观测到多于5颗卫星，几何分布结构好，当低轨卫星运行到覆盖区域之外时，几何分布结构差。

采用星载BDS/GPS试验数据中的GPS观测数据进行自主定轨的结果如图6和图7所示。

图6　GPS自主定轨位置误差

图7　GPS自主定轨速度误差

经过统计，仅采用GPS观测数据进行自主定轨径向、切向和法向的位置误差分别为0.64、0.64和0.86 m；3维位置误差为1.25 m；径向、切向和法向的速度误差分别为1.44、1.28和1.44 mm/s；3维速度误差为2.41 mm/s。

采用星载BDS/GPS试验数据中的BDS观测数据进行自主定轨。结果如图8和图9所示。

图8　BDS自主定轨位置误差

图9　BDS自主定轨速度误差

从图8中可以看出，仅用BDS数据的自主定轨结果的径向、切向和法向的轨道位置和速度误差很不稳定，起伏较大。主要是因为BDS为区域系统，主要覆盖亚太区域，当低轨卫星运行到覆盖区域内，可以观测到多于5颗卫星，定轨精度较为稳定；当低轨卫星运行到覆盖区域之外，观测卫星数减少，无法进行单点定位，自主定轨处于预报中，轨道精度较差。经过统计，仅用BDS的自主定轨结果径向轨道误差在5 m以内，统计RMS值为2.23 m，切向和法向的RMS值分别为2.22和1.99 m；3维位置误差为3.73 m；径向、切向和法向的速度误差分别为3.35、3.68、2.19 mm/s；3维速度误差为5.44 mm/s。

采用星载BDS/GPS试验数据进行联合自主定轨，轨道位置误差如图10所示，速度误差如图11所示。

图10　BDS/GPS自主定轨位置误差

图11　BDS/GPS自主定轨速度误差

经过统计，BDS/GPS联合自主定轨位置误差径向、切向和法向分别为0.62、0.60和0.81 m；3维位置误差为1.19 m；径向、切向和法向的速度误差分别为1.41、1.23和1.41 mm/s；3维速度误差为2.35 mm/s。

统计GPS、BDS和BDS/GPS自主定轨3种方案的位置误差如表5所示，速度误差如表6所示。

表5　不同方案自主定轨的位置误差　m

表6　不同方案自主定轨的速度误差　mm·s-1

将GPS、BDS和BDS/GPS自主定轨3种方案的位置误差进行统计，结果如图12所示。

图12　BDS/GPS自主定轨3种方案的位置误差

从表5和表6以及图12中可以看出：仅采用GPS观测数据的自主定轨和BDS/GPS联合自主定轨的精度相当；而仅采用BDS观测数据的自主定轨精度较差。主要是由于GPS卫星星座是全球均匀分布，从图4可以看出可见卫星数较多而且变化较为平稳，图5中GPS观测数据的PDOP均值为0.87与BDS/GPS的PDOP均值0.82相差很小；而BDS为区域系统，从图3中可以看出BDS的GEO卫星和IGSO卫星主要分布在亚太区域，图4中显示BDS可见卫星数变化较大，图5中显示BDS的PDOP值波动较大。GPS加入BDS观测数据后，自主定轨径向、切向和法向的位置误差分别提高了3.42%、5.09%和5.44%，3维位置误差提高了4.81%。GPS信号发生中断时即仅采用BDS观测数据进行自主定轨时，3维位置误差达到3.73 m，可以满足部分领域轨道位置的应用需求，为改变我国对GPS依赖的局面提供可能。

3　结束语

本文采用高动态信号仿真器生成的星载BDS和GPS仿真数据进行了不同定权策略的BDS/GPS自主定轨精度分析，并进行了BDS、GPS和BDS/GPS自主定轨精度分析，得出以下几点结论：

1)Helmert方差分量估计和顾及动力学模型的Helmert方差分量估计相比经验定权法在切向、法向方向改善较大。顾及动力学模型的Helmert方差分量估计既较好地解决了BDS/GPS观测值的合理定权问题，又有效地减弱了粗差的影响，从而提高了定轨精度。

2)GPS可见卫星数为7～11颗；BDS可见卫星数为3～7颗；BDS和GPS联合可见卫星数为12～16颗。加入BDS后历元可见卫星数增加了5颗左右。GPS和BDS/GPS的PDOP值相差很小，均值分别为0.87和0.82，加入BDS后，PDOP减小了0.05；而BDS的PDOP值则出现较大波动，均值为4.96。

3)仅采用GPS观测数据的自主定轨和BDS/GPS联合自主定轨的精度相当，加入BDS观测数据后，BDS/GPS联合自主定轨径向、切向和法向的位置误差分别提高了3.42%、5.09%和5.44%，3维位置误差提高了4.81%。BDS/GPS联合自主定轨3维位置误差为1.19 m，速度误差为2.35 mm/s。

4)GPS信号发生中断时即仅采用BDS观测数据进行自主定轨时，3维位置误差达到3.73 m，可以满足部分领域轨道位置的应用需求，为改变我国对GPS依赖的局面提供可能。

随着我国BDS系统的快速建设与不断完善，将形成全球分布的卫星导航系统，届时BDS可见卫星数将增多，几何分布结构改善，BDS自主定轨精度将大幅度提高；同时也将进一步体现BDS/GPS自主定轨的优势与更广泛的应用前景。

[1]YANG Yuanxi，LI Jinlong，XU Junyi.Contribution of the Compass satellite navigation system to global PNT users[J].Chinese Science Bulletin，2011，56(26): 2813-2819.doi:10.1007/s11434-011-4627-4.

[2]BERTIGER W，HAINES B，KUANG D，et al.Precise real-time low-Earth-orbiter navigation with the global positioning system(GPS)[EB/OL].(1999-05-26)[2015-08-26].http://ipnpr.jpl.nasa.gov/progress_report/42-137/137B.pdf.

[3]REICHERT A，MEEHAN T，MUNSON T.Toward decimeter-level real-time orbit determination: a demonstration using the SAC-C and CHAMP spacecraft[C]//The Institute of Navigation.Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002).Portland，Oregon:The Institute of Navigation，Inc.，2002:1996-2003.

[4]王甫红.星载GPS自主定轨理论及其软件实现[D].武汉：武汉大学，2006:27-32.

[5]ASHKENAZI V，CHEN W，HILL C J，et al.Real-time autonomous orbit determination of LEO satellites using GPS[C]//The Institute of Navigation.Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997).Kansas City，Missouri:The Institute of Navigation，Inc.，1997:755-761.

[6]MONTENBRUCK O，GILL E.Satellite orbits-models，methods，and applications[M].Springer:Verlag Berlin Heidelberg，2000:123-126.

[7]TAPLEY B D，RIES J C，DAVIS G W，et al.Precise orbit determination for Topex/Poseidon [J].Journal of Geophysical Research Oceans，1994，99 (12): 24383-24404.

[8]赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉：武汉大学，2004-11:36-42.

[9]杨元喜.自适应动态导航定位[M].北京：测绘出版社，2006:303-306.

[10]YANG Y，HE H，XU G.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy，2001，75(2/3):109-116.

Precision analysis on autonomous orbit determination with spaceborne BDS and GPS measurements for LEO satellite

XIONG Chao1，JIA Xiaolin2，3，ZHU Jun4，5，LU Chuanfang1

(1.Xi’an Aerospace Remote Sensing Data Technology Co.，Ltd.，Xi’an，Shanxi 710100，China；2.State Key Laboratory of Geo-information Engineering，Xi’an，Shanxi 710054，China；3.Xi’an Research Institute of Surveying and Mapping，Xi’an，Shanxi 710054，China；4.State Key Laboratory of Astronautic Dynamics，Xi’an，Shanxi 710043，China；5.Xi’an Satellite Control Center，Xi’an，Shanxi 710043，China)

In order to further study on the autonomous orbit determination of LEO satellite with BDS and GPS receiver，the paper discussed the mathematical models of autonomous orbit determination with spaceborne BDS and GPS measurements，presented a method of Helmert variance component estimation considering dynamical model，and then put forward the principle and the process of autonomous orbit determination in details.Based on the self-developed program，the feasibility and precision of autonomous orbit determination were analyzed using the stimulated BDS and GPS measurements generated by high dynamic signal simulator.Result showed that Helmert variance component estimation considering dynamical model could not only resolve the optimal weight of BDS and GPS measurements successfully，but also weaken the impact of gross errors effectively，thus to improve the precision of orbit determination.

autonomous orbit determination；extended Kalman filter；variance component estimation

2015-10-22

国家自然科学基金项目(11503096)；中国博士后科学基金项目(2015M572691)；地理信息工程国家重点实验室基金项目(SKLGIE2014-M-2-3)。

熊超(1986—)，男，湖北麻城人，工程师，研究方向为卫星精密定轨和精密定位。

10.16547/j.cnki.10-1096.20160315.

P228

A

2095-4999(2016)03-0069-08

引文格式：熊超，贾小林，朱俊，等.星载BDS/GPS低轨卫星自主定轨精度分析[J].导航定位学报，2016，4(3):69-76.(XIONG Chao，JIA XiaoLin，ZHU Jun，et al.Precision analysis on autonomous orbit determination with spaceborne BDS and GPS measurements for LEO satellite[J].Journal of Navigation and Positioning，2016，4(3):69-76.)