平板折叠桌的设计参数模型分析

李海燕，王　彦，晏祥高，张梦晨，黄亚群

(云南大学　信息学院，昆明　650091)



平板折叠桌的设计参数模型分析

李海燕，王彦，晏祥高，张梦晨，黄亚群

(云南大学信息学院，昆明650091)

论文建立模型求解创意平板折叠桌的动态变化过程以及设计加工参数。首先，利用平面几何的知识求出不同位置木棒可转动部分和不可转动部分的长度；其次，建立空间直角坐标系，运用立体几何分析的方法表示出每一根木棒两端点的坐标；然后，选择平板状态以及转动最终结束状态对数据进行分析，利用距离公式求出卡槽的长度；最后，用空间直角坐标系表示出木棒末端的坐标及木棒末端与地面的夹角，利用三维空间曲线拟合求出桌角边缘线，并通过夹角与桌角边缘线描述折叠桌运动变化过程。

折叠桌参数；立体几何分析；曲线拟合；Matlab 软件；全国大学生数学建模竞赛

创意平板折叠桌的桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板。桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上，并且沿木条有空槽以保证滑动的自由度。桌子外形由直纹曲面构成，造型美观。

给定长方形平板尺寸为120 cm×50 cm×3 cm，每根木条宽2.5 cm，连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置，折叠后桌子的高度为53 cm。本文试建立模型描述该折叠桌的动态变化过程，并给出该折叠桌的设计加工参数和桌脚边缘线的数学描述。

1　创意平板折叠桌参数求解

1.1转动与非转动部分长度

长方形木板宽度为50 cm，每根木条宽2.5 cm。假设木棒与木棒之间没有间隙，可以得出桌板每一侧存在20根木棒。由于两侧是对称的，所以我们仅研究一侧的情况，每一侧关于宽度中线对称，故仅研究1/4侧的数据[1-2]，即10根木棒，如图1所示。

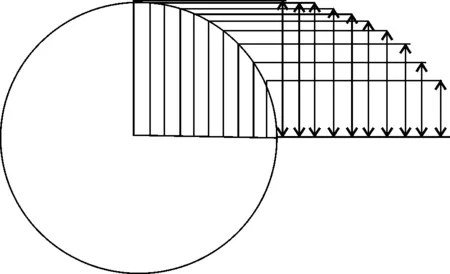
图1　折叠桌支撑木棍平面图

根据圆形的半径及勾股定理，列出方程：

li=60-ri

式中：桌面半径R为50 cm；ri和li分别表示支撑木棍不可移动及可移动部分长度。求解结果如表1所示。

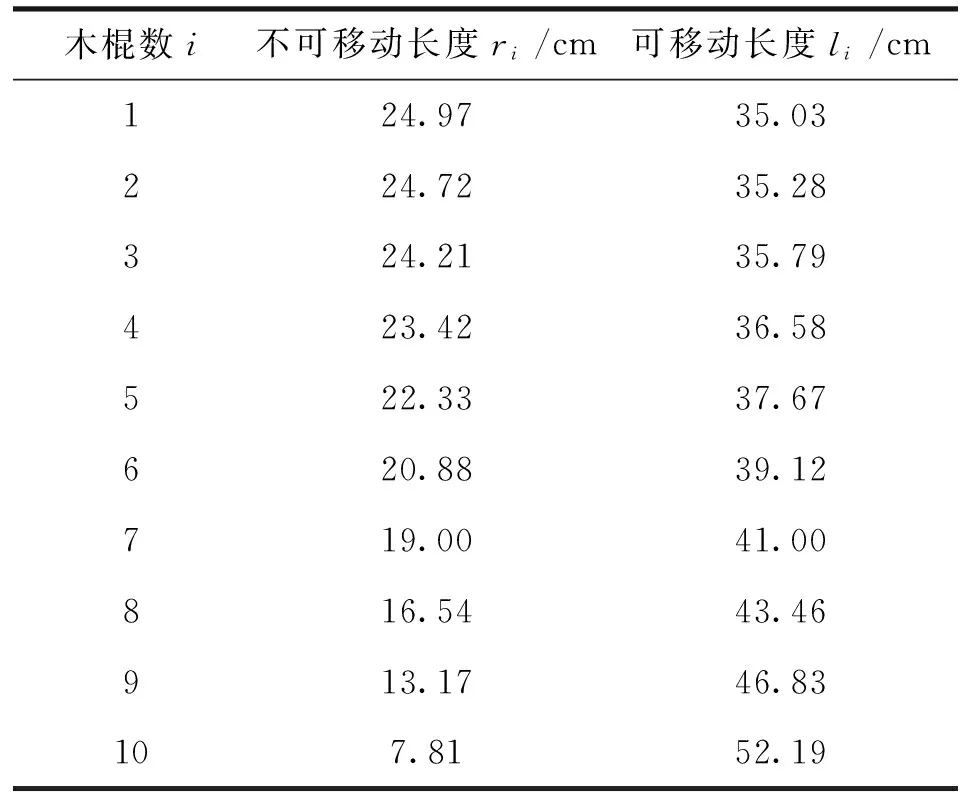
表1　支撑木棍不可移动及可移动部分长度

1.2木条开槽长度

如图2所示，建立空间直角坐标系：以两条钢筋所在的平面为XY平面，X轴在两条钢筋中点连线上，Y轴平行于两条钢筋且到两条钢筋之间的距

离相等，Z轴垂直于XY平面，且穿过桌面的圆心，PiQi为木棒顶端到卡槽最低端的距离，θi是木棒与XY平面的夹角[3-4]。

图2　折叠桌平面坐标系

设O(x，y，z)=(0，0，0)，点P坐标中x与上文r长度对应相同，y坐标可以用1.25(2i-1)确定，z=25。同理，点Q坐标x不变，y随P变化，z=0。根据空间两点距离公式有：

(1)

开槽长度ki=PiQi+ri-30，利用Matlab可以算出所有卡槽长度ki[5]，如表2所示。

表2　折叠桌开槽长度

1.3木棒与地面夹角及动态描述

表3　木棒与XY平面的夹角

从以上数据可以看出，在变化过程中，木棒越短，运动过程中转过的角度越大，同时钢筋在木条卡槽内移动的距离越大，移动的角速度也越快。平板折叠桌开始时与地面所成角度为0，达到稳定状态即钢筋到达木棒卡槽最低端，木棒转到自身可达到的最大角。

2　桌角边缘线数学描述

桌角边缘线上单个点的移动过程可以描述为：当桌子被折叠后，某一桌腿与地面呈一定夹角θ[6-7]。地面水平，过木条与桌面的接触点作垂直于地面的垂线h。根据勾股定理可得：

过木条与钢筋的连接点作垂直于地面的垂线h′，与地面构成一个直角三角形；木条与h和地面构成另外一个直角三角形。两个三角形相似，则有：

该桌脚边缘线的方程表达式为：

求出一侧的20个点的坐标：zi=(li-PiQi)sinθi，y坐标每次增加2.5，xi=15.3-(li-PiQi)cosθi，求出最后状态木条末端坐标见表4。

利用1stOPT进行拟合，得到拟合方程为：

z=1.385-4.383x+0.777x2-0.057x3+

0.002x4-0.027y2

(5)

利用Matlab画出三维图像，如图3所示。

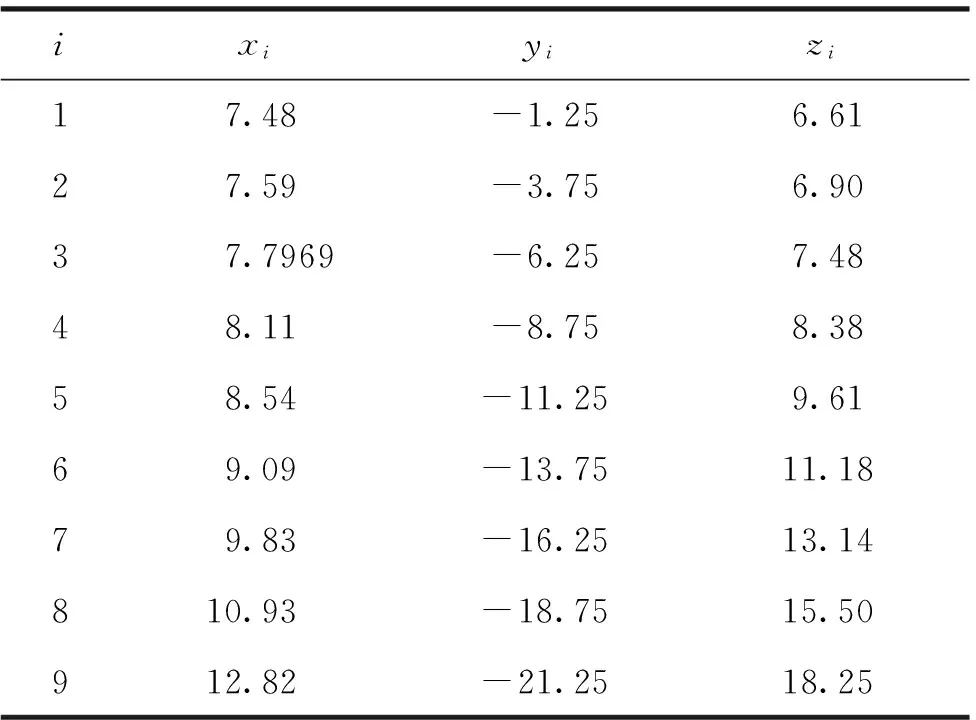
表4　折叠桌稳定时木条末端坐标

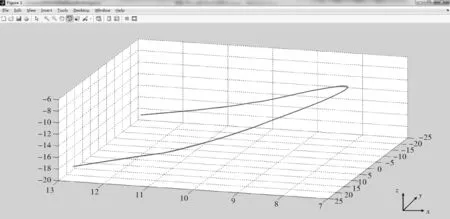
图3　桌角边缘线

3　结束语

文中建立模型求解创意平板折叠桌的动态变化过程以及设计加工参数，包括不同位置木棒可转动部分和不可转动部分的长度，每一根木棒两端点的坐标，卡槽的长度和三维空间曲线。文中建立的平面直角坐标系模型能从数学的角度解决问题，容易完成构建，不但将问题简单化，而且使计算方便。但是在平板折叠桌设计参数模型的最优设计加工参数的求解过程中，没有充分考虑到未知桌子高度和半径的情形。空间直角坐标系模型很容易计算两个点以及数据点之间的距离等参数，但却很难反映数据之间的关系，脱离开三维空间使用时优势不明显。这些问题将在后续研究中解决。

[1]韩中庚. 数学建模方法及其应用[M]. 北京：高等教育出版社，2005.

[2]杨启帆. 数学建模[M]. 北京：高等教育出版社，2006.

[3]曹弋. Matlab教程及实训[M]. 北京：机械工业出版社，2008.

[4]张志涌，杨祖樱. Matlab教程R2008a[M]. 北京：北京航空航天大学出版社，2010.

[5]同济大学数学系. 高等数学[M]. 北京：高等教育出版社，2010.

[6]陈锦昌，刘桂雄，梁利东.自由曲面造型中曲面信息的表示与分析[J].华南理工大学学报:自然科学版，2002，(30)4：26-28.

[7]秦荣. 计算结构力学[M]. 北京：科学出版社，2001.

Analysis on Parameter Model of a Flat Folding Table

LI Haiyan，WANG Yan，YAN Xianggao，ZHANG Mengchen，HUANG Yaqun

(School of Information Science and Engineering，Yunnan University，Kunming 650091，China)

A mathematical model is established to solve the dynamic change process and parameter design of a creative flat folding table. Firstly，the length of the rotated part and un-rotated part of the table stick is computed based on plane geometry. Then a space rectangular coordinate system is built to represent the coordinate points of the two ends of each stick by using the method of three-dimensional geometric analysis. Thereafter，the flat state and the final rotation state are analyzed to calculate the length of slot. Finally，the coordinate of the stick end and the angle between the stick end and the ground are represented by the space rectangular system. The corner of the table edge is drawn by using three-dimensional space curve fitting. Therefore，the dynamic process of the folding table is described by using angle and the table edge line.

folding table parameter; three dimensional geometry analysis; curve fitting; Matlab software; contemporary undergraduate mathematical contest in modeling

2015-01-15；修改日期:2015-07-04

云南大学教改基金资助。

李海燕(1976-)，女，博士，副教授，主要从事人工神经网络方面的研究。

O242.1

A

10.3969/j.issn.1672-4550.2016.01.015