电测法在测量构件力学性能中的应用分析

陈亮亮，张凌凯，乔　箭

(新疆农业大学　水利与土木工程学院，乌鲁木齐　830052)



电测法在测量构件力学性能中的应用分析

陈亮亮，张凌凯，乔箭

(新疆农业大学水利与土木工程学院，乌鲁木齐830052)

电测法是对构件进行应力分析常用的实验方法之一，具有灵敏度高、传感元件小、适应性强等特点，已经成为实验应力分析中应用最广和最有效的方法之一，并在实际工程中得到广泛的应用。依据电测法的基本原理及分析方法，以不等边角钢和工字钢为例，研究分析了在测量轴力、弯矩、扭矩等物理量时的贴片方法、理论推导及实验数据处理。为其他构件进行力学性能参数测量提供一些实验测量方法及技巧，使电测法在实际测量中得到更好的应用。

电测法；构件；力学性能；应用分析

电阻应变测量技术(以下简称电测法)是用电阻应变片测定构件表面的应变，再根据应力、应变的关系式，确定构件表面应力状态的一种应力分析方法，也是当前大学材料力学试验中的重要环节[1-5]。基本原理是:将电阻应变片牢固地粘贴在被测构件上，当构件变形时，应变片的阻值也将随之发生相应的改变；然后通过电阻应变测量装置(即电阻应变仪)将这电阻的改变测出来，并换算成对应的应变值指示出来；最后依据胡克定律计算出被测点应力值的大小。

从应用的角度来看，电阻应变仪实质上是由一个惠斯登电桥组成，其基本关系式表明各桥臂电阻的相对增量(或应变ε)对电桥输出电压的影响是线性叠加的。根据关系式对其恰当地布片与接桥，能够消除荷载偏心与温度变化等因素造成的影响，将不需要的应变成分从结果中排除，测出较准确的物理量值[6-9]。本文以工字钢和不等边角钢为例，研究分析了在测量轴力、弯矩、扭矩等物理量时的贴片方法、理论推导及实验数据处理。

1　分析方法

应用电测法进行实测时，首先，应根据构件表面的应力状态，选择测定点和布置应变片。应力状态有单向应力状态、平面应力状态(主应力方向已知与主应力方向未知两种)两大类。测量点的选择，主要考虑应力集中区和边界上的危险点，同时利用结构和荷载的对称性布点，并在应力已知的部位安排测点，以便测量时监视和检查实验结果的可靠性。其次，要根据电桥的基本特征，选择电桥的最佳接线方式和补偿方法，常用测量电桥的接线方式有半桥接法与全桥接法，补偿方法有温度自补偿应变法、桥路补偿法(补偿块法和工作片补偿法)。恰当合理的布片和接桥，不仅可以消除因荷载偏心造成的影响，也可以消除由于温度变化等因素带来的影响，提高测量精度，从而得出较准确的测量值。根据所需的测量值及相应应力情况，综合分析，确定合理的接桥方式与补偿方法，运用实验的方法测量其大小。

2　实例分析

2.1实例1

壁厚为0.9 mm的薄壁不等边角钢，如图1所示，为了方便加载，在其两端焊接两块对称的连接板，板上分布4个螺孔可以作为加载点，如图2所示。假设C点为该角钢的形心位置(实际加工中有微小位置偏差)，请采用电阻应变测量方法进行如下测量:1)测量该角钢材料的弹性模量和泊松比；2)若B点在该角钢的形心主惯性轴上，试确定B点到C点的距离；3)假设A-A点加载时所产生的弯曲符合平面弯曲条件，请实验确定该角钢的形心主轴方位；4)两端沿D点拉伸力F=1 000 N时，比较角钢长边内，外表面E处主应力(注意加载装置的最大载荷为5 000 N，且只能进行拉伸)。

图1　不等边角钢示意图

由于所测量的构件为薄壁不等边角钢，给出一些基本尺寸，根据截面的主惯性轴的公式计算该构件的形心主惯性轴，并确定其位置，如图2所示。为加载方便在两端焊接的两块对称板，加载时可能造成两端处发生应力集中，所以在选择贴片的位置时应尽量选择在中间部位(特殊固定点除外)。由于该加载装置的最大载荷为5 KN，且只能进行拉伸，当所求的量与加荷载大小无关时采用等量增载法。此处荷载分级为1 KN、2 KN、3 KN、4 KN。同时，可以在应力相同的部位增贴一些应变片，应用串联的方法来减少一些偶然性误差。

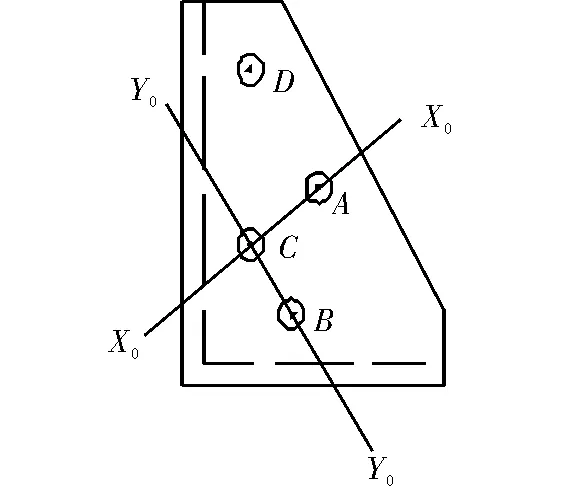
图2　不等边角钢示意图

2.1.1测量该角钢的弹性模量E与泊松比ν

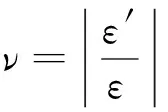
首先，用划针轻轻地在构件地外表面画出主惯性轴的位置，在形心点C加载时，由于加工中可能有微小位置偏差，可能带来弯矩造成的影响。在主惯性轴Y0-Y0，所对应的两侧高度相同的位置粘贴应变片，短边侧贴应变片R1和R2，长边侧为R3和R4，如图1所示。同时也在公共温度补偿块上贴应变片R0与R0′，

本方案采用温度补偿的方法，短边R1和R2，长边R3和R4各自串联的方式，按等量增载法进行加载测量，记下所测的应变值，然后对其结果进行数值处理。求得泊松比为：

2)测量该角钢弹性模量E值的大小。将R1、R2、R3、R4按半桥串联的方式连接，由于加工中造成位置偏心产生弯矩的误差，虽然两侧产生的大小不同，但这样接桥仍然可以抵消一部分弯矩造成的影响，剩余的相对更小可以忽略不计。理论推导关系式如下:εY=ε1.3-ε2.4=(εP+εT)-(-vεP+εT)=εP(1+v)。εP为R1与R3串联，抵消一部分弯矩影响后的应变，-νεP为R2与R4串联，抵消一部分弯矩影响后的应变，εT为对应的各自温度变化造成的应变。由于E=σ/ε，σ=P/A则对应的关。按等量增载法进行加载，实验后记下所测的应变值，然后对其进行数值处理，取其平均值:

即:

2.1.2试确定B点到C点的距离

由于B点在该角钢的形心主惯性轴上，在B点等量加载可产生在主惯性轴Y0-Y0弯矩。设B点到C点的距离为L，即M=P·L。在R1与R3所在主惯性轴的下部等高位置分别贴上R1′与R3′，其接桥方式仍然采用串联的方法，这样可以尽可能地减小误差。

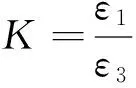
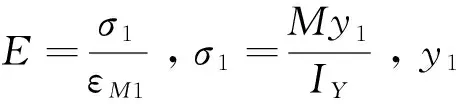
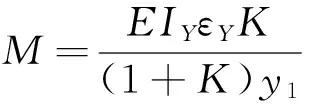
(3)

由于

M=PL

(4)

将式(4)带入式(3)得:

(5)

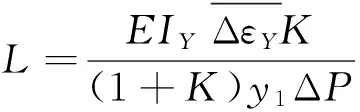
2.1.3在A点加载，确定该角钢的形心主轴位置

在另一主惯性轴X0-X0上贴一对应变片R5和R5′，贴片的位置如图1所示。由于A点不在任一主惯性轴上，加载后产生的弯矩在X0与Y0主惯性轴的分量必不为零，通过测量两主惯性轴上的应变，建立应变量与对应坐标上的弯矩的关系式，推出A点加载引起MX、MY的大小。AC与另一主惯性X0-X0轴的夹角为α=arctan(MX/MY)。接桥方式为半桥串联式。

设在A点加载时，引起的弯矩在X0与Y0主惯性轴上的分量为MX、MY，根据关系式E=σ3/ε3，E=σ5/ε5，σ3=MYy3/IX，σ5=MXy5/IY，y3、y5分别为点3和点5到形心的水平距离，则根据以上公式推得:

(6)

同样应用等量增载法进行加载，处理数据后取平均值，代入式(6)求解出角度，即：

2.1.4采用等量加载法的数据记录和处理

当两端沿D拉伸力F=1 000 N时，E点处于一般的平面应力状态(主应力方向未知)，由于主应力的方向难以确定，所以需要在E点内外两侧分别贴应变化。根据应变测量的普通规律求其主应力的大小和方向，经常运用的应变花有三片直角﹑三片等角﹑四片直角﹑四片等角4种。四片直角式优点是比三片直角多一片，这使的它能核对测量值，因为互为垂直的应变之和是一常数，即ε1+ε3=ε2+ε4。四片等角应变花的优点是，如果知道某测点的主应力方向时，可使第4片沿着假设的主应力方向贴片，

测得数据代入公式，可以得到很大的简化。结合测量点E的应力情况，选择四片直角式应变花较好。测得数值后，代入公式中计算求得主应力的大小与方向。然后比较E点内外主应力的大小，分析其原因。其贴片方式如图3所示。主应力大小求解公式为:

(7)

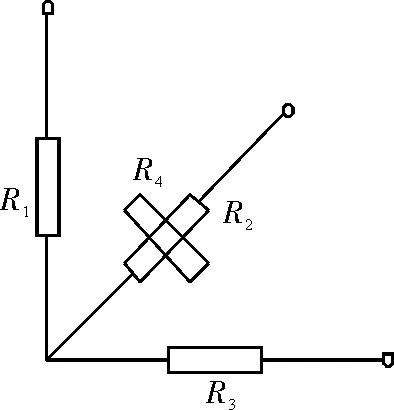
图3　电桥接线方式

2.2实例2

某工字钢结构承受复杂载荷，在其横截面上，同时存在着轴力FX、剪力FY、扭矩MX、铅垂弯矩MZ和水平弯矩MY。已知材料的弹性模量为E，泊松比为ν。试用电测法分别测出这五个内力分量各自引起的最大应力(不计扭矩MX引起的扭矩约束正应力)，给出各个应力分量与应变仪读数应变之间的关系式。

2.2.1求解与轴力FX、铅垂弯矩MZ和水平弯矩MY相应的最大正应力σFx、σMy和σMz

根据工字钢的各个应力分布分析，确定最大应力的位置。应用最大正应力法求解，其贴片位置在如图4所示的R1、R2、R3处，由于剪力FY扭矩MX在3个顶角处产生的应力为零，在应变片上不产生相应的应变，故不予考虑。其接桥方式采用串联方式。

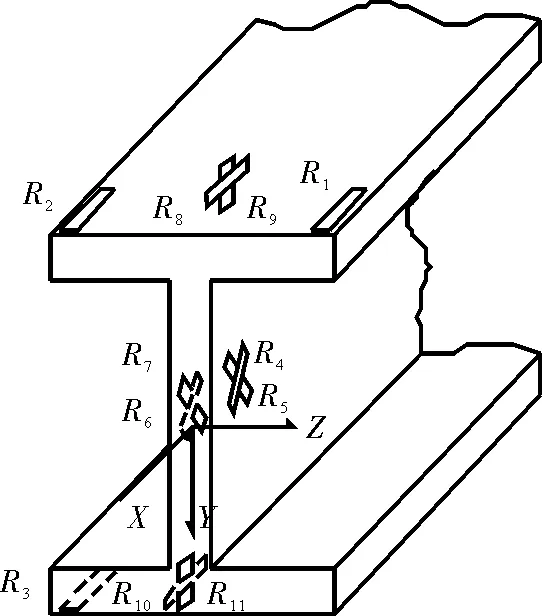
图4　工字钢示意图

列应变方程组如下:

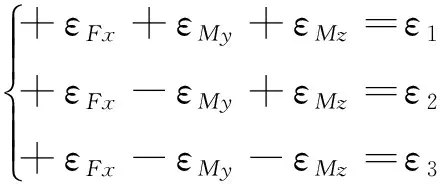
(8)

式(8)中三式联立可求得εFx、εMy、εMz的大小，即：

εFx=ε1+ε3/2

εMy=ε1-ε2/2

(9)

εMz=ε2-ε3/2

由于各点都处于单向应力状态，即最大正应力σFx、σMy和σMz与应变仪读数的关系式为:

(10)

2.2.2求解剪力FY产生的最大切应力τY

根据工字钢在剪力FY作用下的应力分布分析，最大切应力在X-Z轴所在的平面内，在其平面内，贴两对应变片分别为R4和R5、R6和R7，如图4所示。在应变片上产生应变外荷载有轴力FX、剪力FY、水平弯矩MY、扭矩MX，铅垂弯矩MZ的数值为零，因为弯矩MZ在轴线上产生应变。接桥方式为全桥式。

(11)

依据接桥方式，应变仪的读数与各应变片的关系式为:

εY=ε4-ε5+ε6-ε7=4(εFy-εMz)

然后应用上式求得εMz=ε2-ε3/2联立求解εFy的大小，建立应力与应变的关系。

2.2.3求解扭矩MX产生的最大切应力τX

在X-Y轴的所在的平面内，工字钢上下两表面贴两对应变片分别为R8和R9，R10和R11，如图4所示。在该应变片上，水平弯矩MY产生的应变为零，其余都产生相应的应变。列应变方程式如下(接桥方式为全桥式):

(12)

依据接桥方式，应变仪的读数与各应变片的关系式为:εY=ε8-ε9+ε10-ε11=4εMx。根据几何变形关系及广义胡克定律推得:τX=2GεMx。

则τX=GεY/2，即扭矩MX产生的切应力与应变仪读数的关系式为τX=GεY/2。

3　结束语

电测法不仅用于验证材料力学的理论，而且作为一种重要的工程测试手段，为解决工程实际问题及从事科学研究提供了良好的实验手段。本文从介绍电阻应变测量技术的原理出发，对不等边角钢和工字钢进行了详细的叙述分析，探讨了应用电测法测量的基本思路，对构件如何进行应力分析、布片、接桥，如何能够减小误差以及相应数据的处理方法等等问题的探索，对相关力学性能参数进行了测量，重要的是对于其他构件的力学性能值的测量在理论分析与实验测量方法方面提供一些参考方法。但是也遇到一些问题，如应变片的粘贴位置、测试环境的变化以及粘贴技术的水平等等，都会直接影响到测量的结果。如何解决这些不利因素所产生的影响，完善电测法的应用，也是我们值得考虑的问题。

[1]孙训方，方孝淑.关来泰.材料力学(Ⅰ)[M].北京:北京教育出版社，2002.

[2]刘鸿文.高等材料力学[M].北京:高等教育出版社，1985.

[3]张如一，陆耀桢.实验应力分析[M].北京:机械工业出版社，1981.

[4]熊丽霞，吴庆华.材料力学实验[M].北京:科学出版社，2006.

[5]王育平，边力，腾桂荣等.材料力学实验[M].北京:北京航空航天大学出版社，2004:2.

[6]梁立凯.电阻应变片测量中温度为误差的补偿方法[J].呼伦贝尔学院学报，2001(2):72～73.

[7]郑秀瑶，谢大洁.应力应变电测技术[M].北京:国防工业出版社，2003.

[8]王琦.电测法在应变测量中的应用简述[J].潍坊高等职业教育，2009，5(4):67-68.

[9]夏祁寒.应变片测量原理及在实际中的应用[J].山西建筑.2008，34(28):99-100.

Analysis on Mechanical Properties of Materialsin Using Resistance Straingauge Method

CHEN Liangliang，ZHANG Lingkai，QIAO Jian

(College of Water Conservancy and Civil Engineering，Xinjiang Agricultural University，Urumqi 830052，China)

The resistance straingauge method is commonly used in the actual components of the stress analysis of the experimental method，because of its high sensitivity，small sensors and high adaptability.The testing way has became one of the most extensive and effective methods in the practical engineering.This paper introduces the composition and the working principle of the resistance straingauge method，analysing the method of attaching resistance straingauges and dealing with data.What’s more，it can provide some skills and theoretical principle to solve some questions in other materials，which is important to the application in practice.

resistance straingauge method; components; mechanical properties of meterials; analysis

2014-11-20；修改日期: 2015-01-19

新疆维吾尔自治区水利水电工程重点学科基金(xjslgczdxk20101202)；新疆农业大学实验室建设与管理改革项目——基于大学生创新项目的实验室开放的研究与实践。

陈亮亮(1981-)，男，博士生，副教授，实验室主任，主要从事固体力学理论方面的研究和实验教学。

TP301;TM93

A

10.3969/j.issn.1672-4550.2016.01.006