电场对非平整基底上液滴铺展特性的影响

赵盼盼，戴宇晴，叶学民，李春曦

(华北电力大学 能源动力与机械工程学院，河北保定071003)



电场对非平整基底上液滴铺展特性的影响

赵盼盼，戴宇晴，叶学民，李春曦

(华北电力大学 能源动力与机械工程学院，河北保定071003)

基于润滑理论和漏介电质模型，通过建立电场作用下非平整基底上液滴铺展的演化模型，利用PEDCOL程序模拟了导电液滴在非平整基底上的铺展特征。结果表明：非平整基底有助于加快液滴的铺展速度，其中，锯齿状基底下液滴的铺展速率最大；底部电势为恒定值时，电场对液滴铺展起抑制作用；线性底部电势将诱导液滴中心出现偏移现象，且液膜轮廓呈现与基底外形相似的特征；增加基底波数或高度，均有利于液滴铺展，但其影响总体较小。

电场；液滴；铺展；非平整基底

0　引言

放置在固体表面或预置液膜上的导电液滴，在电场作用下呈现铺展、破裂、重组或电润湿等现象，其影响因素包括麦克斯韦应力、电毛细力和分离压等，通过改变电场可显著改变导电液滴的运动学特征，这一过程在矿物浮选、湿式电除尘优化及医疗等领域有着广泛的应用和前景[1-3]。

带电液滴与壁面接触面间的相互作用引出许多值得探讨的电水动力学问题，有研究者通过在基底表面人为设置凹坑或倾斜基底来研究液膜在基底表面的热质传递性能。文献[14]研究了零雷诺数时液膜在电场作用下沿倾斜波纹状基底上的铺展，发现随韦伯数增大，液膜铺展速度加快且铺展愈加稳定。在此后研究，文献[15-17]进一步提出了描述小幅度甚至是中幅度阶跃基底上的渐进模型，分析了重力驱动液膜沿电场存在且有周期性缺口的倾斜基底的铺展过程；其结果表明，可采用长波近似法分析电场对液膜自由表面毛细状隆起的影响，导电液膜进入凹槽前毛细隆起高度与电场强度成反比，由此指出稳定条件下可通过调节电场强度来控制液膜表面变形及与相对波纹基底的相位差，进而消除下台阶区域薄膜出现的毛细状隆起结构。文献[18]比较了电场作用下理想导体和漏介电质液膜在不同基底上的动力学特性，指出理想导体的平滑曲面出现不稳定现象，而漏介电质液膜依然稳定铺展。文献[19,20]对两相不相溶液体中的液滴在直流电场中的变形进行了模拟，表明外加电场较小时液滴随时间呈现振荡状态，过强的电场则使液滴挣脱表面张力，失去稳定进而导致液滴破裂。文献[21]研究了径向电场作用下粘性流体在垂直纤维制品上的动态特征，指出电场不改变振幅和流动速率、长波速度在外电场作用下随振幅增加而减小。

综上所述，针对电场作用下平整壁面上的液滴运动特征已开展了大量研究，而非平整壁面上的液滴运动研究尚不完善，且多数研究是针对定常流动，而关于电场和基底对液滴的非定常运动影响的研究还较少。为此，下文开展恒定电势作用下液滴在不同基底上的动力学特性，分析不同电场和基底形态对铺展特征的影响。

1　理论模型和特征演化方程

1.1理论模型

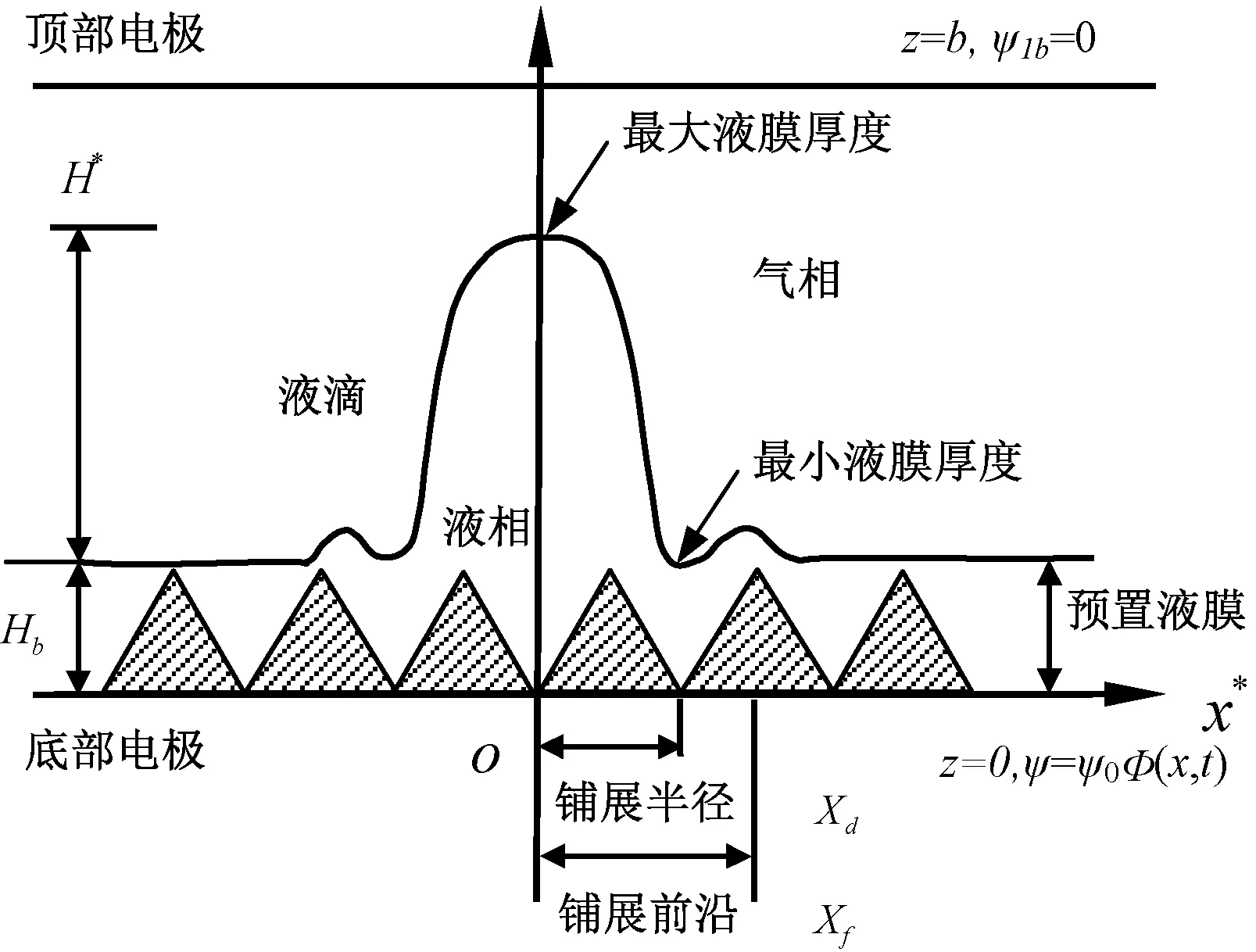
图1　非平整基底上液滴的铺展示意图

如图1所示，基底函数为s(x)，基底高度为D，基底上预置一层厚度均匀为Hb-s(x)的液膜。液滴铺展而成的液膜与预置液膜交界处，形成铺展前沿，最大液膜厚度Hmax、铺展半径Xd和铺展前沿Xf是描述铺展特征的重要参数。假设液滴为不可压缩牛顿流体，壁面为无滑移无渗透界面，液滴自由表面外为无粘性气体。液滴初始最大厚度H与流动方向尺度L相比非常小，即∈=H/L<<1，适用润滑理论[22]。

1.2控制方程

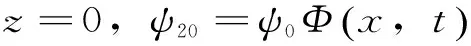
获取分析信息能力作为考纲要求的四种能力之一，常常是学生的薄弱能力。如果，教师一方面能充分挖掘教材中的各种信息素材，另一方面利用试题素材充分训练学生获取信息，利用信息解决问题的能力，那么也许学生在面对新情境的信息试题时，会更加有信心与方法！

描述界面电荷密度q的方程[22]93为

(1)

无量纲水动力学[23]控制方程组为

(2)

(3)

(4)

无量纲边界条件为

(5)

(6)

(7)

(8)

(9)

结合式(1)～式(9)，通过积分运算可得液膜厚度和界面电荷密度的演化方程组为

(10)

(11)

2　数值模拟

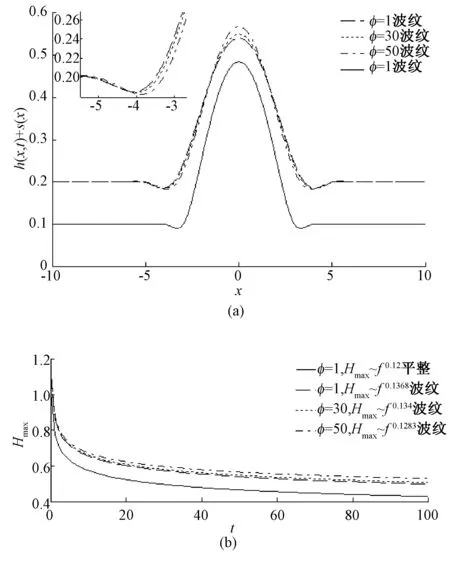
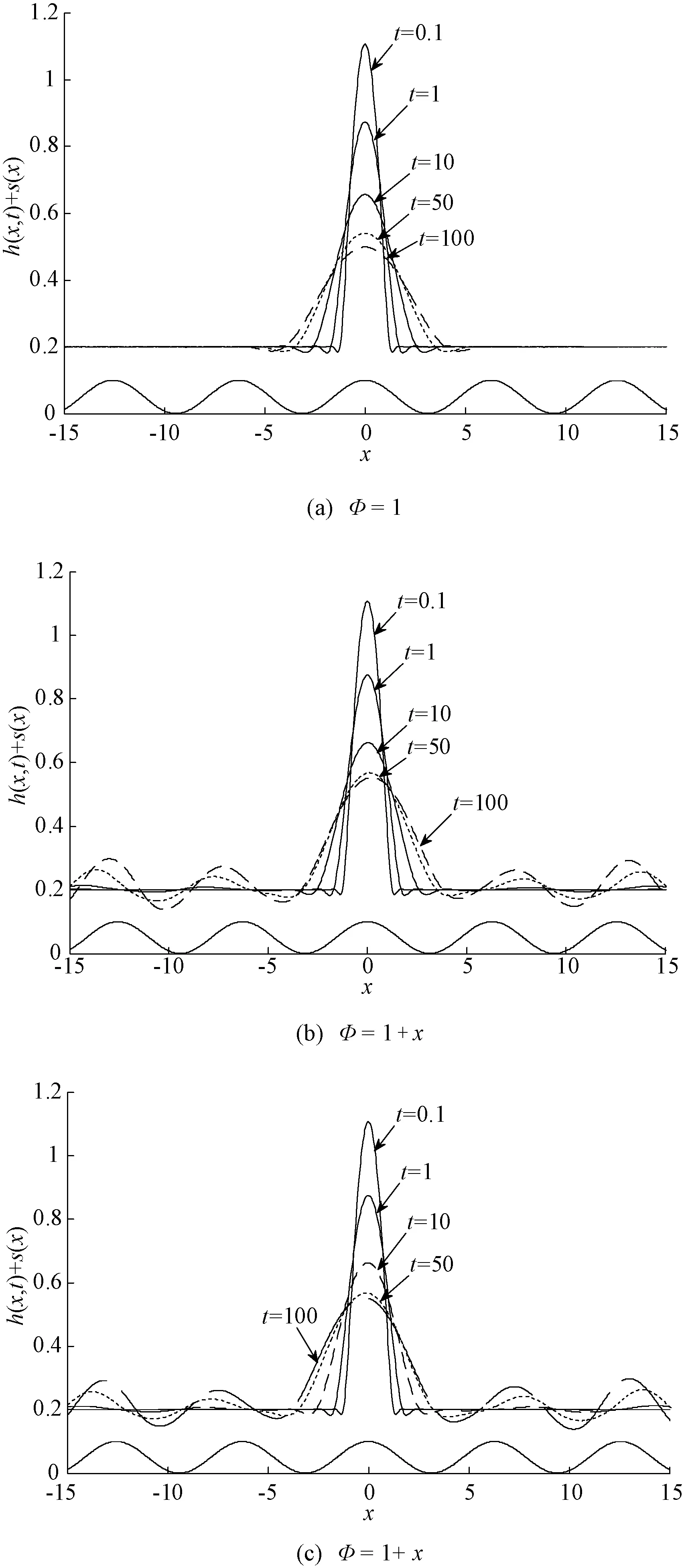
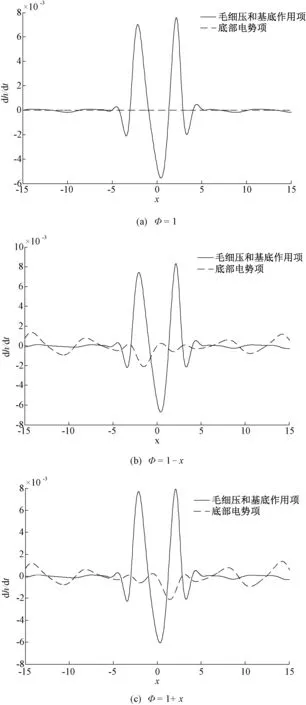
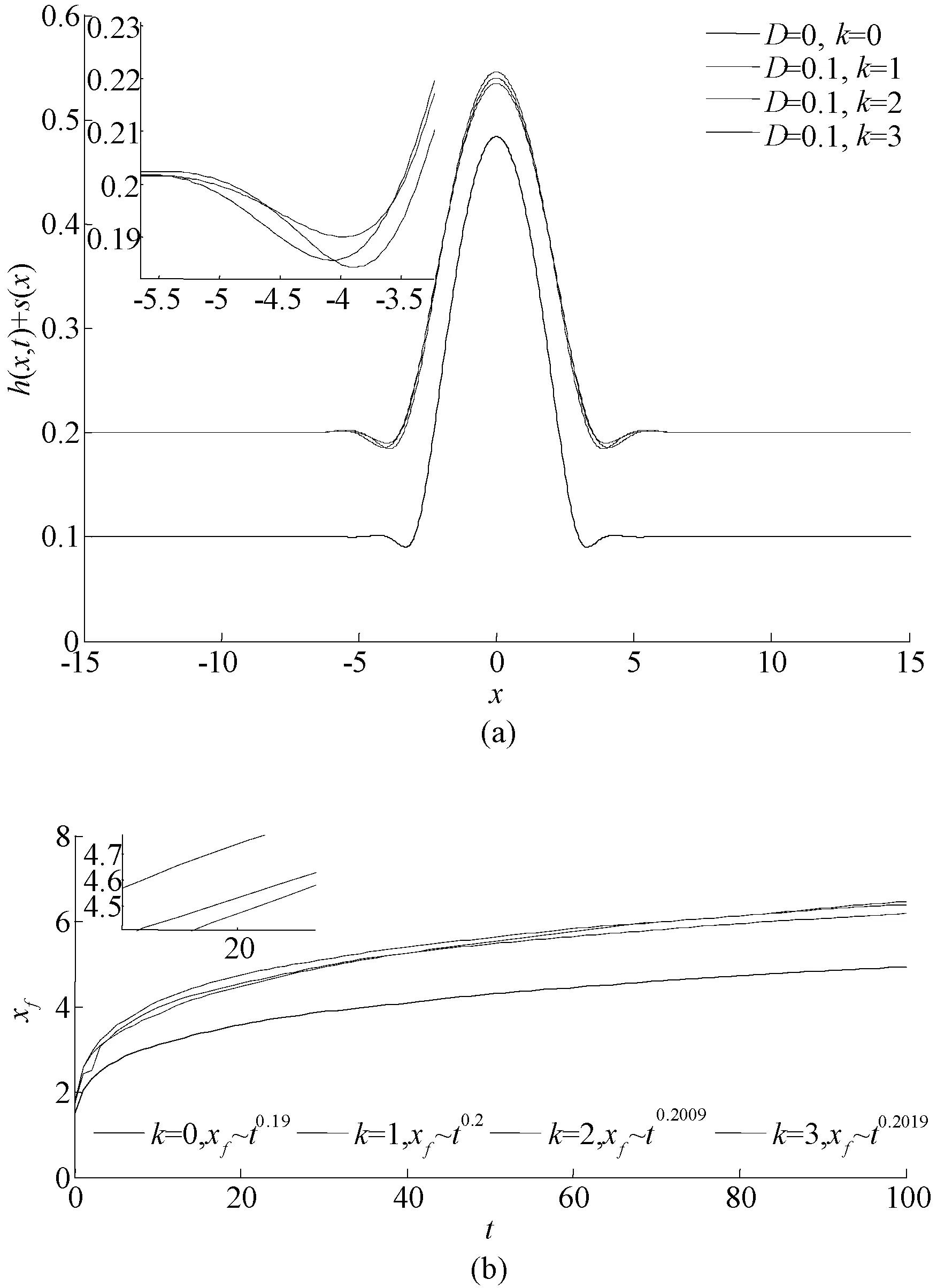
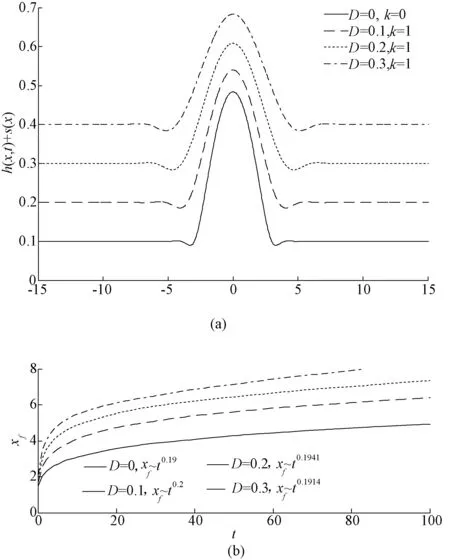
采用PEDCOL程序[24,25]求解演化方程式(10)和式(11)，该程序为基于Petrov-Galerkin有限元法和非均匀网格Gear时间分析法的高效数值计算程序，可有效求解非线性抛物型偏微分方程，已广泛应用于相关领域研究中。选取-15

程序中的初始条件为：

(12)

(13)

波纹状基底函数为：

(14)

锯齿状基底函数为：

(15)

三角状基底函数为：

(16)

梯形状基底函数为：

(17)

式中：F(x)=0.5[1+tanh(100x)]为海氏阶跃函数；s(x)为基底函数，由于s(x)是关于x的任意函数，通过改变s(x)，可得不同特征的基底表面。其中，无特殊说明时无量纲预置液膜厚度Hb=0.2。

程序中的边界条件

(18)

3　结果分析

3.1不同基底的影响

对基底施加恒定底部电势Φ=1，不同基底上导电液滴铺展过程的特征参数变化如图2所示。图2(a)表明，平整基底上最大液膜厚度随时间的减小率为Hmax～t-0.12，与此相比，非平整基底上Hmax的减小率均有所增加，其中锯齿状基底下的Hmax～t-0.16减小速率最快，其次为梯形状和波纹状基底下的Hmax～t-0.14，最次为三角状基底下的Hmax～t-0.13，由此表明，基底表面的不平整性对液滴铺展过程有明显影响。

图2　不同基底上液滴特征参数的变化

由图2(b)和2(c)可知，基底的外形结构也显著影响液滴的铺展半径Xd和铺展前沿Xf。与平整基底的Xd～t0.17相比，锯齿状基底下液滴铺展稍有加快，为Xd～t0.18；波纹状和梯形状基底同锯齿状相比，其不平整度有所增加，因而液膜局部压力变化幅度增大，所以液滴向两侧铺展的速度比锯齿状基底快，为Xd～t0.19；三角状基底下液滴向两侧铺展的速度增加最快，为Xd～t0.20。铺展前沿的变化率依次为：锯齿状Xf～t0.215，三角状Xf～t0.203，波纹状和梯形状Xf～t0.200，均比平整基底时的Xf～t0.190要快。这是因基底表面的不平整度将影响液滴铺展速率，与三角状、波纹状和梯形状基底相比，锯齿状基底的不平整度最大，由此使液滴铺展成的液膜表面变形显著增大，进而其铺展前沿随时间的变化速率最快。

3.2不同电场强度的影响

为研究电场强度对液滴铺展特征的影响，以波纹基底为例，对液滴施加恒定电势Φ=1、30和50进行对比。图3(a)为t=50时液滴铺展示意图，观察x=0处h(x，t)+s(x)可知，随底部电势增大，Hmax下降幅度减小；相对于平整基底上铺展过程，波纹状基底时，液滴向两侧铺展有所加快，但不同电场强度下的液滴铺展半径和铺展前沿基本保持不变。图3(b)表明，随底部电势值增加，Hmax随时间的变化率减小；其中，Φ=1时Hmax～t-0.1368减小得最快，其次为Φ=30的Hmax～t-0.134，当Φ=50时，为Hmax～t-0.1283。

图3　不同恒定电势对液滴铺展的影响

3.3不同电势形式的影响

实际应用中，液滴所处电场不仅仅局限于恒定电场，还可根据不同应用场合，通过改变电场形式进而控制液滴铺展过程。如图4(a)所示，Φ=1时，液滴向两侧对称铺展，与平整基底上的铺展特征类似。当改底部电势形式为Φ=1+Sx，图4(b)和4(c)分别为S=-1和1时液滴的铺展形态。由图可知，在基底波谷处形成凹陷，波峰处形成隆起，这是因在电场力和基底共同作用下波峰/波谷处液膜表面压力不同所致。随时间持续，液膜变形区域逐渐扩大、且变形愈加明显，并逐渐呈现与基底轮廓类似的表面波形。观察最大液滴高度所在位置可知，在线性电势作用下，液滴分别呈现右移和左移现象，这与文献[26]所得模拟结果一致。

图4　不同电势下波纹状基底上液滴的铺展

图5　不同作用力分析图

为进一步探讨液滴呈现上述不同形态的内在原因，图5给出了液滴铺展过程中的各作用力变化。由式(10)可知，方程右侧第1项为底部电势作用项，第2项为毛细压和基底共同作用项。在恒定电势Φ=1下，液滴受电毛细压和基底的共同作用，作用力主要集中在液滴上，预置液膜区域受影响很小，因此液滴向两侧均衡铺展而成的液膜未出现任何波动。当S=-1和1时，因液滴铺展半径处于基底第一波谷处，毛细压和基底及底部电势作用明显，加快了液滴向两侧铺展的速率，并在此处出现凹陷。当S=-1时，液滴中心左侧底部电势作用强于右侧，此时左侧底部电势起减小液膜厚度而右侧起增大液膜厚度的作用，表现为液滴整体右移；受基底影响，表面呈现波纹状特征；S=1时电势作用方向与S=-1相反，液滴向左偏移。

3.4不同基底参数的影响

为分析基底波数k和高度D对铺展过程的影响，图6给出了t=50时液滴的铺展特征。图6(a)表明，当D=0.1，k=0，1，2，3时，在相同铺展范围内，液膜经过的基底波数增多，从而抑制了液滴铺展过程，最大液膜厚度的减小率降低并接近平整基底情形。图6(b)表明，随波数k增大，铺展前沿的变化率依次减小，当k=3时，非平整基底上的铺展前沿变化率已接近平整基底时的Xf～t0.19。由此表明，增加基底波数可能抑制液滴铺展，对液滴铺展速度影响较小。

图6　不同波数下的铺展特征

图7给出了k=1，D=0，0.1，0.2，0.3时的铺展特征。该图表明，随基底表面的不平整度增大，液滴高度不断减小并始终保持对称形状向两侧铺展，且铺展前沿逐渐增大；非平整基底上的铺展前沿变化率略高于平整基底时的Xf～t0.19，表明增大D有助于加速液膜铺展过程。

图7　不同基底高度下的铺展特征

4　结论

(1) 基底形式的改变对液滴的铺展速度有显著影响，锯齿状基底最大液膜厚度Hmax减小速度最快，梯形和波纹状基底次之，三角状基底最慢，但均明显快于平整基底。

(2) 恒定电势对液滴铺展过程有明显的抑制作用，增大Φ值时，电场力对液滴铺展的作用加强，最大液膜厚度减小速率变慢；恒定电场对液滴的影响体现在垂直方向上，铺展半径和铺展前沿无明显变化。

(3) 底部电势形式为Φ=1+Sx，当S=-1和1时液滴的铺展形态整体呈基底轮廓状，液滴铺展中心分别呈现右移和左移特征。

(4) 增加基底波数或基底高度，有利于液滴铺展过程，铺展前沿变化率均高于平整基底情形，但其影响总体较小。

[1]SAVILLE D A. Electrohydrodynamics: The taylor-melcher leaky dielectric model[J]. Journal of Fluid Mechanics, 1997, 29: 27-64.

[2]叶学民, 李春曦, 曹罕, 等. 表面活性剂溶液铺展过程中的分离压特性[J]. 电力科学与工程, 2012, 28(5): 21-27.

[3]张军, 何宏舟. 高压静电破乳中离散液滴的动力学分析[J]. 化工学报, 2013, 64(6): 2050-2057.

[4]王玮, 李志信, 过增元. 粗糙表面对微尺度流动影响的数值分析[J]. 工程热物理学报, 2003, 24(1): 85-87.

[5]张程宾, 陈永平, 施明恒, 等. 表面粗糙度的分形特征及其对微通道内层流流动的影响[J]. 物理学报, 2009, 58(10): 7050-7056.

[6]GERBIG Y B, PHANI A R, HAEFKE H. Influence of nanoscale topography on the hydrophobicity of fluoro-based polymer thin films[J]. Applied Surface Science, 2005, 242(3-4): 251-255.

[7]朴明日, 胡国辉. 壁面结构对非定常薄膜流动表面波特性的影响[J]. 计算物理, 2011, 28(6): 843-852.

[8]叶学民, 姜凯, 李春曦. 含胶束结构的活性剂溶液非均匀铺展演化模型研究[J]. 华北电力大学学报(自然科学版)， 2012, 39(3): 88-93.

[9]BONTOZOGLOU V, PAPAPOLYMEROU G. Laminar film flow down a wavy incline[J]. International Journal of Multiphase Flow, 1997, 23(1): 69～79.

[10]ORON A, HEINING C. Weighted-residual integral boundary-layer model for the nonlinear dynamics of thin liquid films falling on an undulating vertical wall[J]. Physics of Fluids, 2008, 20(8): 082102.

[11]D’ALESSIO S J D, PASCAL J P, JASMINE H A. Instability in gravity-driven flow over uneven surfaces[J]. Physics of Fluids. 2009, 21(6): 853-857.

[12]朴明日, 胡国辉. 均匀电场对沿波纹壁面下落液体薄膜稳定性的影响[J]. 水动力学研究与进展, 2011, 26(3): 368-376.

[13]TSELUIKO D, BLYTH M G, PAPAGEORGIOU D T, et al. Effect of an electric field on film flow down a corrugated wall at zero Reynolds number[J]. Physics of Fluids, 2008, 20(4): 2103-2123-19.

[14]TSELUIKO D, BLYTH M G, PAPAGEORGIOU D T, et al. Electrified viscous thin film flow over topography[J]. Journal of Fluid Mechanics, 2008, 597(6): 449-475.

[15]TSELUIKO D, BLYTH M G. Effect of inertia on electrified film over a wavy wall[J]. Journal of Engineering Mathematics, 2009, 65(3): 229-242.

[16]TSELUIKO D, BLYTH M G, PAPAGEORGIOU D T. Electrified film flow over topography at zero Reynolds number: at analytical and computational study[J]. Journal of Engineering Mathematics, 2011, 69(2): 169-183.

[17]ARUNA R, SATISH K. Electrohydrodynamics deformation of thin liquid films near surfaces with topography[J]. Physics of Fluids, 2014, 26(12):159-221.

[18]张军, 何宏舟, 黄冠星. 均匀电场中液滴变形特性的耗散粒子动力学模拟[J]. 化工学报, 2014, 65(10): 3872-3877.

[19]白莉, 倪玲英, 郭长会, 等. 乳状液液滴在高压直流电场中的变形与破裂分析[J]. 应用力学学报, 2013, 30(1): 76-79.

[20]DING ZIJING, XIE JINLONG, TECK N W, et al. Electrohydrodynamics deformation of thin liquid films near surfaces with topography[J]. Physics of Fluids, 2014, 26(12): 1-18.

[21]ZHAO Y. Physical mechanics of surface and interface [M]. Beijing: Science Press, 2012:185-186.

[22]CRASTER R V, MATAR O M. Electrically induced pattern formation in leaky dielectric films [J]. Physics of Fluids, 2005, 17(17):93-106.

[23]赵盼盼. 电场作用下液滴的铺展特性[D]. 保定：华北电力大学, 2016.

[24]CONROY D T, MATAR O K. Thin viscous ferrofluid film in a magnetic field[J]. Physics of Fluids, 2015, 27(9): 437-463.

[25]KOVALCHUK N M, MATAR O K, CRASTER R V, et al. The effect of adsorption kinetics on the rate of surfactant-enhanced spreading[J]. Soft Matter, 2016, 12(4): 1009-1013.

[26]YEO L Y, CRASTER R V, MATAR O K. Drop manipulation and surgery using electric fields[J]. Journal of Colloid and Interface Science, 2007, 306(2): 368-378.

Effect of Electric Field on Droplet Spreading on Uneven Substrate

ZHAO Panpan, DAI Yuqing, YE Xuemin, LI Chunxi

(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

An evolution model on uneven substrate is established, based on the leaky dielectric model and theory of lubrication, to analyze the spreading of a conductive droplet in the presence of electric field. The PEDCOL program is applied to the numerical simulation during modelling. Results show that the uneven substrate can accelerate the speed of spreading, and the maximum rate occurs when the droplet spreads on serrated basement. The spreading of droplet is suppressed in the constant electric field. When the electric potential becomes linear, deviation from the droplet centre appears with its spreading profile similar to that of uneven substrate. Increasing the wave number or height of the substrate facilitates the droplet spreading, but the effect is relatively weak.

electric field; droplet; spreading; uneven substrate

2016-04-17。

国家自然科学基金(11202079)；河北省自然科学基金(A2015502058)。

赵盼盼(1989-)，女，硕士研究生，研究方向为微观流体力学理论与应用，E-mail:huadianzhaopanpan@126.com。

O361；TQ021

A

10.3969/j.issn.1672-0792.2016.08.009