修船厂移泊作业优化方法研究

唐伟炜，杨坤荣，艾志兴（.华南理工大学 土木与交通学院，广东 广州 5064；.中船澄西船舶（广州）有限公司，广东 广州546；.中船黄埔文冲船舶有限公司，广东 广州 5075）



修船厂移泊作业优化方法研究

唐伟炜1，杨坤荣2，艾志兴3
（1.华南理工大学 土木与交通学院，广东 广州 510641；2.中船澄西船舶（广州）有限公司，广东 广州511462；3.中船黄埔文冲船舶有限公司，广东 广州 510715）

船舶泊位调度是修船厂作业的重要组成部分，本文基于动态规划和图论的相关理论，对修船厂码头移泊调度问题进行了研究，阐述了移泊系统的马尔科夫特性，并将船厂码头移泊问题就转化为求解其所对应的赋权网络最优路问题，通过对问题网络结构图的逆向推进，把一个最优路径问题转化为多段决策问题，最终获得该问题的最优路径。最后用算例证明了本文研究的方法对于处理修船码头移泊问题，有着非常好的寻优性。

修船厂移泊调度；马尔科夫链；图与网络模型；最优路径

引　言

船舶泊位调度是修船企业码头作业的重要组成部分，随着修船行业的发展，各修船厂码头停靠船舶的数量以及多样性不断增加，人员工作量日益增大。事先对修船厂码头各个泊位的停泊计划进行合理安排，可以极大地提高修船码头的作业效率。通常情况下，船厂的船舶泊位问题可以定义为：在计划周期开始时，对计划周期内预计抵达的船舶合理地安排停泊时间和靠泊位置，并由于某些特定原因，对一艘或者多艘船舶进行位置调整，也就是泊位调整。由于修船厂码头泊位数量是有限的，船舶越靠近码头，起重机作业范围越佳，工程需求越能得到满足，当各泊位组同时停泊数艘船时，就需要不断的去移泊，调整泊位，使各船可以交替使用起重设备，满足不同船舶的工程要求。

依靠调度人员经验来管理的船舶调度系统在实际操作时，由于现场的局限性，计划表中的任务有时无法完成，并现场会有些突发状况使方案要随时更改，这就加大了工人工作量，降低了工作效率。而且由于方案边做边落实，未能直观的在停靠船舶数量以及多样性不断增加的情况下，难免会有重复工作的现象。

由此可见，这种由人力来制定移泊计划在码头船舶较多时已逐渐不能满足生产需求，以至于企业资源无法充分利用，运行成本过高。为了提高生产效率，降低生产成本，减轻工人作业量，亟需一套新的方法来解决问题。

本文依据船厂船舶停泊的特点，即移泊过程容易离散的特征，通过分析移船作业过程，抽象归纳问题的基本要素，逐步建立问题的数学模型，然后寻找解答问题的方法。

1　移泊问题描述

修船码头的泊位为一个二维泊位，分别由横向岸线与纵向档位组成一个二维空间，如图 1所示。

图1　码头泊位布置

每艘船舶都存在一个最佳工作泊位，最佳工作泊位即能最大限度的保障船舶在计划周期内完成作业的泊位，由于设备工作范围的局限性，一般越靠近码头岸线的泊位越能提前安排作业。在企业接到预定进厂船舶的船期表时，会给船舶制定停泊计划和作业计划，但当码头船舶较多时，新进厂船舶则需暂停其他泊位，在开始作业前经一系列移泊移到最佳工作泊位，其次，当船舶停泊到目标泊位后，若勘探的工作量与与其工作量有差别，因工作计划的调整也需要对船舶进行移泊，此外，需要移泊的情形通常还有：1）船舶因进出坞造成的泊位调整；2）因船舶的进出厂造成泊位的调整；3）发生干扰事件后，因预定靠泊位置被其他船舶占用造成的泊位调整。在实际生产中移泊原因通常不是单一的而是由各种因素复合而成的。

当船舶需要从一个泊位移动到另一个泊位时，制定移泊方案目标一般为移船次数最少，一般来说，船舶移动次数与移动时间成正比，船舶移动次数越少，移动路径越简单，所花费时间也就越少。这样既能确保船舶在计划周期内完成作业，又能使码头环境不那么复杂，降低安全事故的发生率。而船舶在水中被拖轮拖移的速度可认定为一常数。船厂的移泊任务按要求顺利完成首先取决于船厂码头移泊资源（泊位和拖轮），修船厂的泊位由岸线和沿航道宽度方向的档位构成，码头岸线的长度和航道的宽度决定着船舶可停靠数量；同时移船工具—拖轮的数量和马力，也对移泊进程和优化路径有着关键性的影响，往往拖轮的数量和马力大小决定着每次移泊的船舶数量，若拖轮数量不足或马力太小，可同时移动的船舶数量就会减少。另外，船厂码头的系泊能力和码头外航道的通行能力等，也会限制码头的容量，间接地影响了移泊的进程。所以求移泊最优路径的核心问题就是合理利用有的码头资源，寻找一个最佳的移船方案，对移泊过程进行优化，使船舶的移动次数最少，这也就是建立问题的模型以及求解的过程。

2　移泊问题的马尔科夫特性

马尔科夫过程一种典型的随机过程［1］。通过对不同状态的初始概率以及状态之间的转移概率的研究，来确定状态的变化趋势，从而达到对未来进行预测的目的。马尔科夫链是指时间和状态参数都是离散的马尔科夫过程，是最简单的马尔科夫过程。每个满足离散性、随机性、无后效性3个特点的系统，均可用马尔科夫链研究其过程，并预测未来。

从直观上看，船舶在码头停靠的形式似一个矩阵，假设初始状态为 A0，即船舶未开始移泊前的状态。该矩阵经过n次变化，变为矩阵An，即船舶移泊后的最终状态，也是目标状态。这时，我们可以将整个移泊过程离散成n个子系统，每个子系统对应着一次遵循着一定演化规则的船舶排列变化，而且每个子系统的状态只与其前后状态相关。此时，整个船舶移泊系统可以看成一个离散体系。

按照马尔科夫链的定义，可知由n个离散系统所组成的船厂码头移泊系统可以看成为一个马尔科夫链，它具有无后效性的特征，即在某个状态已经确定的情况下，它的后续状态只受当前状态的影响，跟以前的状态无关，换言之，当前状态就是后续状态的初始状态；具有离散性的特征，即整个船舶移泊作业过程可以看成由n个子系统构成，每一个子系统对应着一个船舶移动的方案。解决问题的关键就是寻找系统内各状态间的演化规则，从而得出系统的最优路径。

3　船舶移泊调度问题的图与网络模型

对于建立修船厂的船舶移泊模型问题，国内外研究很少涉猎，相关的内容主要集中在交通运输与车辆调度上，比较典型的有图与网络的最短路径问题［2］，其模型的建立也值得我们参考。面对的一个现实问题，到底什么样的方法建立数学模型，没有绝对的标准，不同的人可能使用不同的方法，另外，同样的问题，可以用几个阶段来完成模型，不同的阶段有不同的方法，组合起来形或完整模型，数学模型的形式可以是多种多样的，可以是表格形式，也可以以图形的形式，不一定非得有数学公式才算是数学模型［1］。

图与网络中所谓的“图”并不是通常意义下的几何图形或物体的形状图，而是指某类具体事物和这些事物之间的联系，是以一种抽象的形式来表达一些确定的事物之间的联系的数学系统［3］。借助于图论的概念、理论和方法，可以对任何一个包含了二元关系的离散系统的数学模型求解。

由网络图形成的特性，我们知道一个移泊作业方案的形成，就是寻找一系列从初始状态到目标状态的决策，而这些决策则对应着网络图中的某一条路径，所以我们可以把移泊作业问题转化为多阶段赋权单向网络模型。问题描述如下：假定有一网络，其顶点为移泊作业的某个状态，其S=｛s1，s2，…，sn｝是顶点集，E=｛eij｝是边集，eij=（si，sj）表示连接顶点si和sj的边，且称这两个顶点与边 eij相关联。顶点 s0为问题的初始状态，顶点st为问题的最终状态，每一个决策值对应着一条有向边，从状态si到状态sj时，所经过的每条路径都是所做的决策，即移泊的动作组合。由状态和路径所构成的网络图包含从初始状态到最终状态的所有路径，其中也包括了最优路径。这样，就将求船厂码头最佳移泊方案的问题转化为求解决其所对应的赋权网络最优路问题。移泊作业的决策过程是一个不可逆过程，具有单向的特征，所以其最优途径就是该网络最优路径［4］。

船舶码头多阶段赋值见图2。

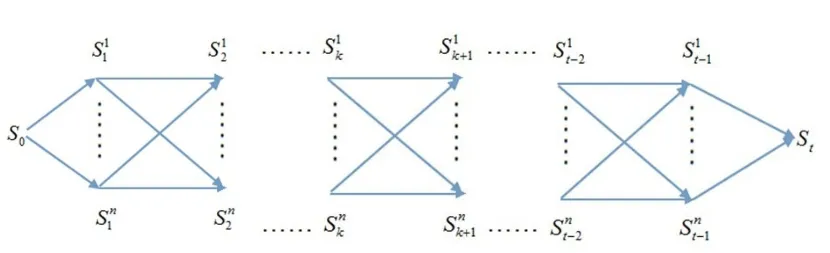
图2　船舶码头多阶段赋值

图2中要求从出发地s0到达目的地st，首先，可将图2划分为t个阶段，然后逆向依次寻求距离最小的最短路径。第一阶段，从st-11到st只有一条路线，同样从st-21到st-11也只有一条路线。到了第二阶段，从st-21到st有st-21-st-11-st，st-22-st-12-st，…，st-2n-st-1n-st共 n条路线，选择最优的一条。同理可知st-22到st之间的最短距离，第三阶段也依次继续进行下去，这样就把一个最优路径问题转化为了多段决策问题。求解过程如图3。

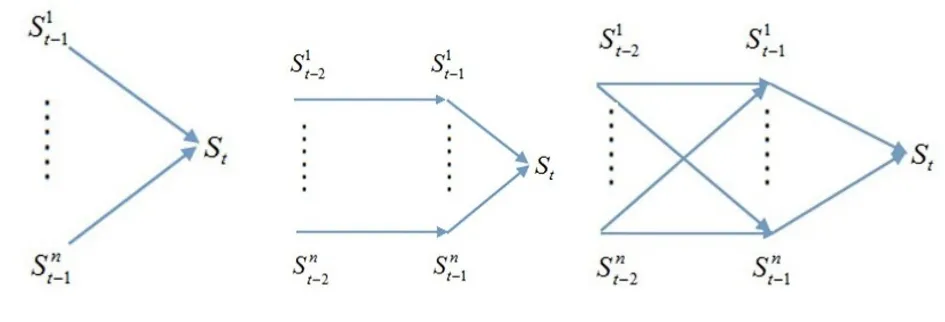
图3　动态规划求解过程

4　算　例

在t0时刻码头原始停泊布置如图4所示，在t0时刻码头共停靠16艘船，（3，4）处为目标泊位，（1，3）处为目标船舶，码头泊位为5×6的矩阵，要求将图中目标船舶移到目标泊位。

图4　原始泊位布置

用matlab按照上节求解步骤编写程序后最优移泊路径如图5。

图5　最优移泊路径

按照优化计算方法，总的移船艘次为3次。从结果看，该模型和求解方法有着很好的优化计算结果，与传统人工制定方案相比，能直观的提供移泊路线方案，这就避免了一些重复的动作，节省了作业时间，为企业节约了成本。

5　总　结

本文阐述了船厂码头移泊作业的马尔科夫特性，船舶移泊作业是一个逐渐演化的过程，具有无后效性，离散性的特征，针对这些特点，提出了码头移泊作业问题的图与网络模型，将移泊问题转化成多阶段决策问题，给出寻找最优路径方法，并给出了模型的一般算法思路和流程。最后通过实例的计算分析，证明了本文的研究方法对寻找移泊最佳路径问题有着很好的指导作用。

［1］陈光亭，裘哲勇.数学建模［M］.北京：高等教育出版社，2010：191-197.

［2］司守奎，孙玺菁.数学建模算法与应用［M］.北京：国防教育出版社，2011：37-39.

［3］王庚，王敏生.现代数学建模方法［M］.北京：科学出版社，2010：4-8.

［4］Jianping Chen，Jiawei Ye.The Graph Model and the Dijkstra Algorithmic of the Ship Shifting and Berthing Operation at the Dockyard［C］.ISOPE-2011，Vol.3：1207-1214.

Optimization Research of Berth Shifting Operation of Ship-repairing Dock

Tang Weiwei1，Yang Kunrong2，Ai Zhixing3
（1.Civil and Transportation Institute，South China University of Technology，Guangzhou Guangdong 510614，China； 2.CSSC Chengxi Shipyard （Guangzhou） Co.，Ltd.，Guangzhou Guangdong 511462，China；3.CSSC Huangpu Wenchong shipbuilding Co.，Ltd.，Guangzhou Guangdong 510715，China）

Ship berth adjustment is an important part of Ship-repairing dock operation.The berth shifting of ship-repairing dock is studied on the basis of dynamic programming and relevant content of graph theory.An introduction is given to markov property of berth shifting system，and the berth shifting problem is transformed into the solving process of the corresponding optimal path of empowerment network.Through the reverse propulsion of network structure，an optimal path problem is eventually converted into the multiple-stage decision problem so as to get the optimal path of the problem at last.The calculation example verifies that the above method can optimize the berth shifting process of ship-repairing dock well.

shifting of ship-repairing dock； markov chain； figure & network model； the optimal path

U673

A

1004-9592（2016）04-0056-04

10.16403/j.cnki.ggjs20160414

2015-05-13

唐伟炜（1983-），女，博士，主要研究方向为船舶与海洋结构物制造。