例谈“三角代换”法证明不等式

洪木山（福建省南安第一中学）

例谈“三角代换”法证明不等式

洪木山
（福建省南安第一中学）

变量代换是解决数学问题的常用技巧，在高考试卷特别是数学竞赛中出现频繁。对于一些结构比较复杂，变元较多而变化关系不太清楚的不等式，可以适当引进一些新变量替换（或者部分替换）原来的变量，从而简化结构，凸显特征，是转化与化归的数学思想的重要体现。三角代换是一种常用的代换方法，下面通过举例子来说明用“三角代换”法证明不等式。

例1.设x1，x2，y1，y2∈R，证明

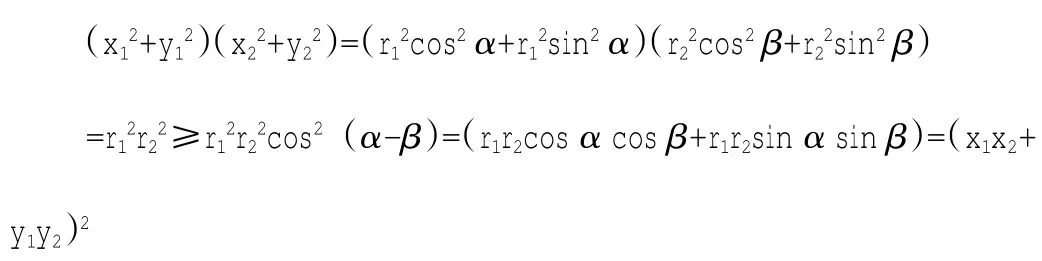
当x1，x2，y1，y2不全为零时，其中等号当且仅当cos（α-β）=±1时取得，

即当x1=λx2，y1=λy2时，等号成立。

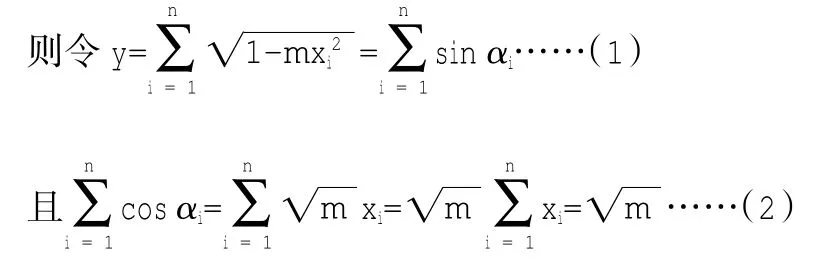
于是y2≤n2-m，即故原不等式得证。

说明：两道题的证明都采用了三角代换的技巧，事实上形如a2+b2≤r2的结构均可以考虑作类似的三角代换。三角代换不止于此，还可以将代数等式或不等式与三角恒等式进行类比，从而得到所需要的形式新颖的不同代换。

·编辑王团兰