动力总成悬置系统优化与减振分析*

陈　克， 李晓政， 周霜霜

(沈阳理工大学 汽车与交通学院， 沈阳 110159)



动力总成悬置系统优化与减振分析*

陈克， 李晓政， 周霜霜

(沈阳理工大学 汽车与交通学院， 沈阳 110159)

为了解决汽车动力总成悬置系统隔振问题，建立了某型号动力总成悬置系统的仿真模型.针对悬置系统无阻尼和有阻尼的情况，对支反力进行了对比分析；选取四个橡胶悬置的12个主方向刚度为设计变量，以动力总成悬置系统在各阶固有频率主振方向上的能量解耦程度为目标函数，利用Adams/Insight模块对动力总成悬置系统进行优化，结果显示优化后的悬置系统支反力明显降低，减小了动力总成振动的传递，解耦程度有了明显的提高，通过优化悬置系统的减振效果有了很大的改善.

动力总成； 悬置系统； 振动； 刚度； 阻尼； 支反力； Adams/Insight模块； 能量解耦； 优化设计

由于汽车市场发展越来越快，人们对汽车的乘坐舒适性越来越重视.其中，发动机的减振是急需解决的问题之一，动力总成悬置系统的设计研究也显得越来越重要，合理地匹配悬置系统参数是提高整车性能的关键.目前，多采用优化方法对悬置系统的刚度参数进行优化，匹配合理的悬置系统刚度，以减小发动机传递到支承系统的振动[1-3].但悬置系统的结构形式、几何位置及悬置系统的结构、刚度和阻尼等特性直接影响悬置系统的减振性能[4-5]，因此，在匹配悬置系统参数时不但要考虑悬置系统的刚度，还要考虑悬置系统的阻尼.

本文以某动力总成悬置系统为研究对象，基于振动微分方程理论，建立动力总成的多刚体动力学模型，分析悬置在有、无阻尼状态下的减振情况，进而在考虑悬置系统阻尼特性情况下，优化悬置的刚度参数来减小支反力大小，从而降低振动的传递，减小动力总成悬置系统的振动，并求解系统的固有频率和主能量分布方向上的解耦程度.

1　动力总成悬置系统

汽车在路上行驶时，主要的振源为发动机的激励和路面的不平度激励，然而随着道路条件越来越好，发动机激励对振动的影响就越来越明显，为了减小这种影响，需要动力总成悬置系统具有较好的减振性能.

动力总成的悬置系统中，通常用橡胶元件作为悬置装置来联接动力总成与车体，所以动力总成的固有频率不高(一般都低于30 Hz)，因此，可以把动力总成看作刚体.考虑阻尼和激励的工况下，动力总成悬置系统的振动微分方程[6]可表示为

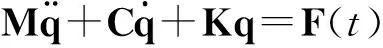
(1)

式中：M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；q为系统的广义坐标；F(t)为系统所受的广义力矩阵.

在考虑系统阻尼的情况下，令F(t)=0即可得到系统六自由度的自由振动微分方程.在系统阻尼和外激励都不考虑的情况下，令C=0、F(t)=0即可得到系统六自由度的自由振动微分方程.

能量解耦基本原理是在求得系统自由振动方程的基础上，求出系统的固有频率与固有振型，它每一阶的主振动动能和势能之和是保持不变的，不同阶的能量也是互不变换的.如果系统以第j阶模态振动来分析的话，它的能量分布矩阵可以表示为

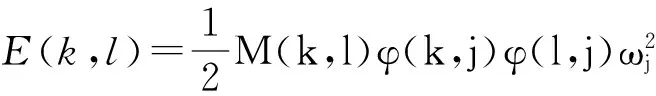
(k，l，j=1，2，…，6)

(2)

式中：M(k，l)为系统质量矩阵的第k行，第l列；φ(k，j)、φ(l，j)为系统第j阶振型第k、l个元素；ωj为系统六阶固有频率.

动力总成悬置系统的振动频率求解方程为

f=ni/60τ

(3)

式中：n为发动机转速；i为发动机气缸数；τ为冲程系数，两冲程为1，四冲程为2.

2　动力总成模型建立

在保证动力总成悬置系统的质心和各悬置相对位置不变、动力总成质量不变的情况下，把动力总成进行简化[8-9].在UG中建立动力总成悬置系统的几何模型，并导入Adams中建立的动力总成悬置系统6自由度的仿真模型如图1所示.动力总成悬置系统的惯性矩及悬置元件特性参数如表1、2所示(表1中，m为总成悬置系统质量，I为惯性矩).

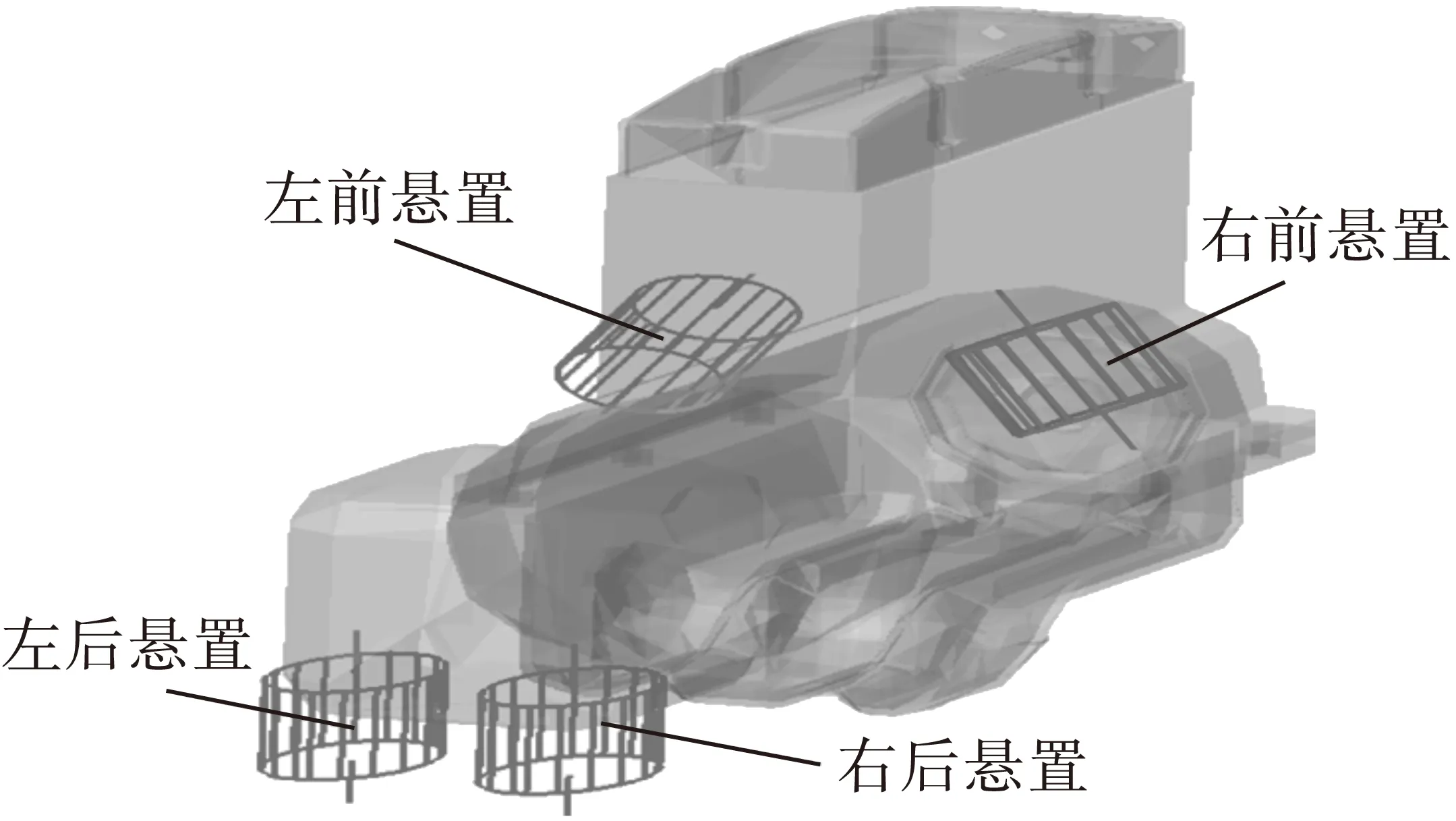
图1　动力总成悬置系统6自由度仿真模型

表1　动力总成惯性矩参数

表2　动力总成悬置元件特性参数

3　动力总成悬置系统仿真分析

在Adams的Vibration模块中，对模型进行频域振动仿真分析，在Vibration Analysis选项中进行求解设置并选择模态分析，启动能量解耦组件[10]，可获得动力总成在各阶模态下的振型，如图2所示.由图2可以看出三阶模态振型和五阶模态振型耦合程度较高，且动力总成存在一定的扭转振动.

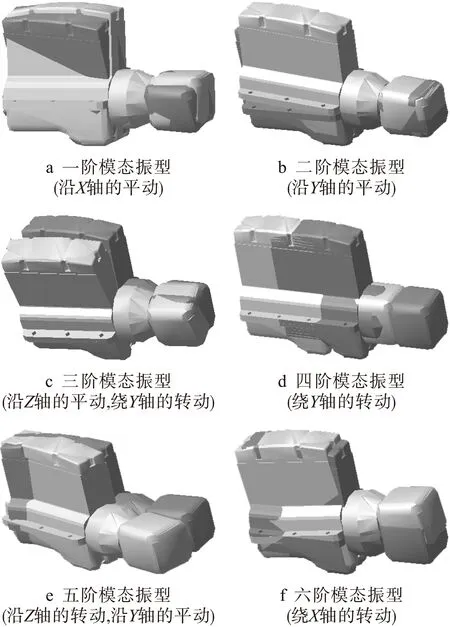
图2　动力总成悬置系统各阶模态振型

时域分析主要针对怠速工况(n=700 r/min)进行仿真分析，图3～10为系统在怠速工况下，悬置无阻尼和有阻尼时悬置垂直方向支反力随时间变化的曲线.

图3　无阻尼怠速工况下左前悬置支反力

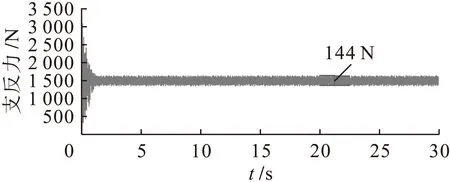
图4　有阻尼怠速工况下左前悬置支反力

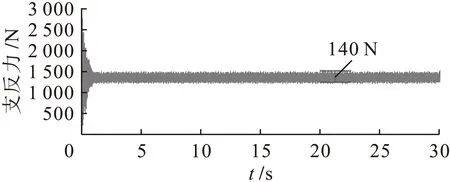
图5　无阻尼怠速工况下右前悬置支反力

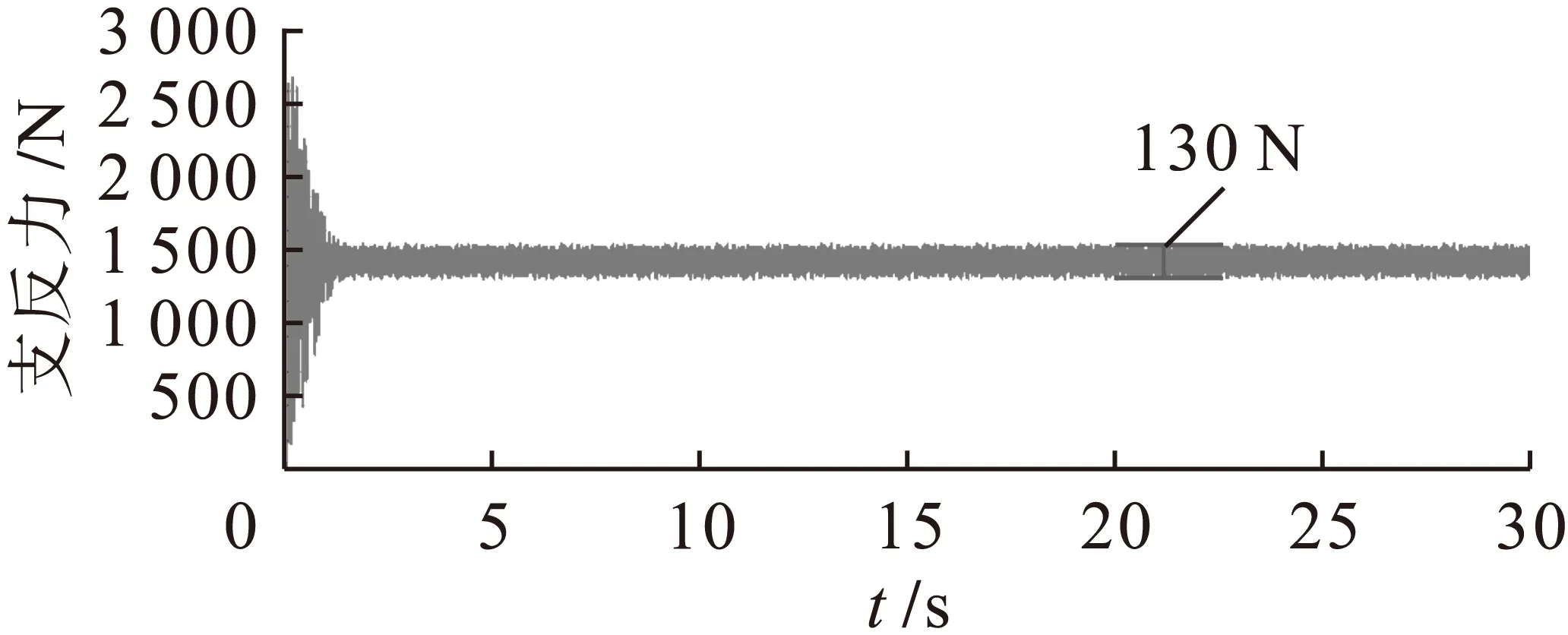
图6　有阻尼怠速工况下右前悬置支反力

图7　无阻尼怠速工况下左后悬置支反力

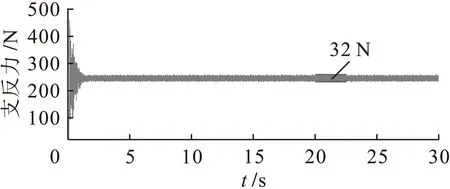
图8　有阻尼怠速工况下左后悬置支反力

由图3～10中可知，考虑阻尼时，在怠速工况下左前悬置垂直支反力稳定在1 510 N左右，其波动幅值由158 N减小为144 N；右前悬置垂直支反力稳定在1 400 N左右，其波动幅值由140 N减小为130 N；左后悬置垂直支反力稳定在250 N左右，其波动幅值由35 N减小为32 N；右后悬置垂直支反力稳定在230 N左右，其波动幅值由28 N减小为26 N.这说明振动在通过橡胶悬置时由于阻尼的存在而减小的更多，所以在减振分析时不能够忽略橡胶悬置的阻尼参数.

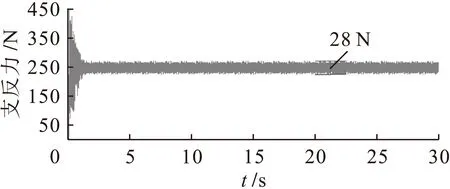
图9　无阻尼怠速工况下右后悬置支反力

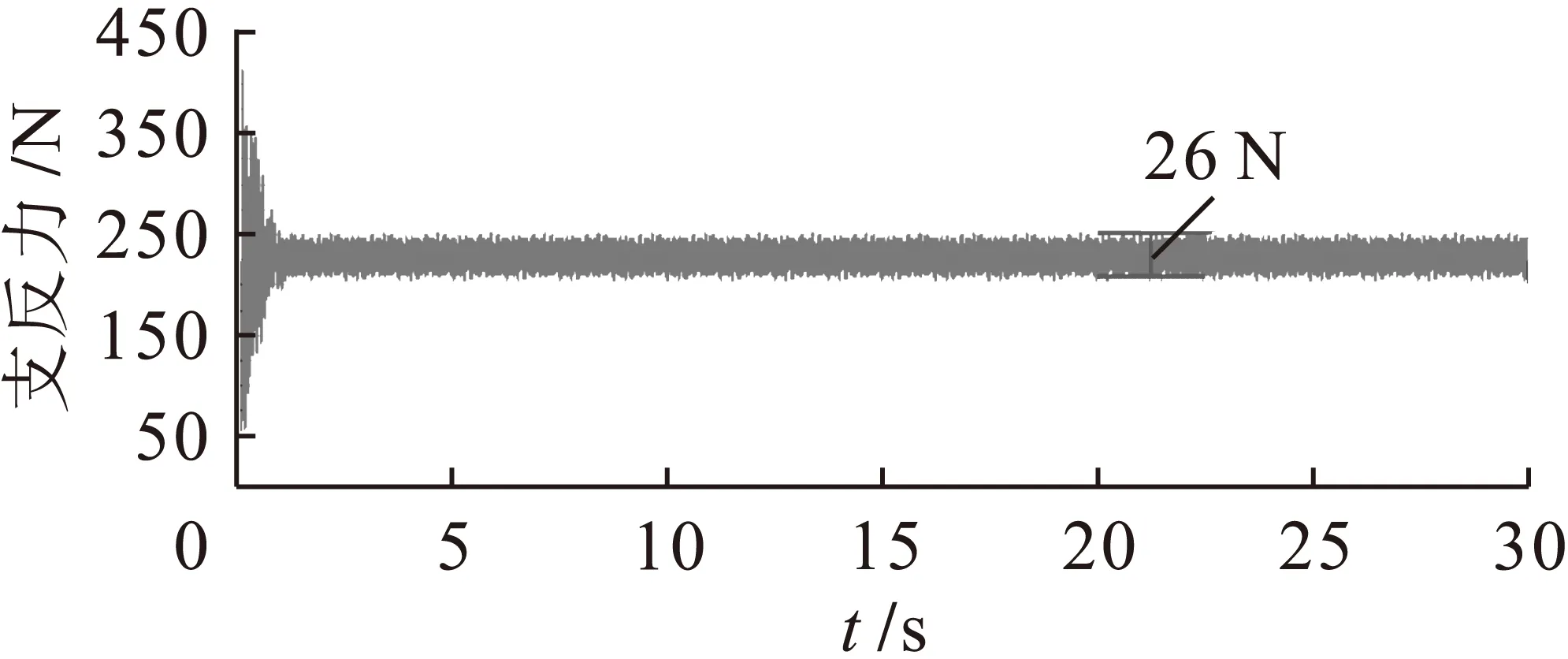
图10　有阻尼怠速工况下右后悬置支反力

4　动力总成悬置系统优化分析

本文对动力总成悬置系统采用insight模块进行优化分析，在怠速工况下对6自由度悬置模型进行参数优化设计.

4.1动力总成悬置系统优化

由于4个悬置主方向上的刚度对悬置系统的减振效果都有一定的影响，故选取设计变量为4个悬置的12个主方向刚度，取值范围为上下变动50%，即

59.5 N/mm≤DV_Fflx≤178.5 N/mm

376.3 N/mm≤DV_Ffly≤1 128.9 N/mm

266 N/mm≤DV_Fflz≤798 N/mm

59.5 N/mm≤DV_Ffrx≤178.5 N/mm

376.3 N/mm≤DV_Ffry≤1 128.9 N/mm

266 N/mm≤DV_Ffrz≤798 N/mm

141 N/mm≤DV_Frrx≤423 N/mm

26.05 N/mm≤DV_Frry≤78.15 N/mm

57 N/mm≤DV_Frrz≤171 N/mm

141 N/mm≤DV_Frlx≤423 N/mm

26.05 N/mm≤DV_Frly≤78.15 N/mm

57 N/mm≤DV_Frlz≤171 N/mm

对动力总成悬置系统来说，其约束条件主要是：约束刚度的变化范围为±50%，系统固有频率的约束变化范围为5～16.4 Hz.

若把能量在其各阶主振方向上的解耦情况作为动力总成悬置系统优化设计的目标，可把动力总成主振动能量分布的加权和最大设为目标函数.由式(2)可得当系统第j阶模态振动时，第k个广义坐标分配到的能量占系统总能量的百分比为

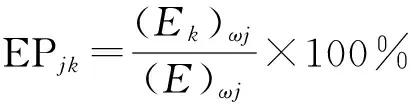
(4)式中，EPjk为系统的解耦程度，若其值为100%，即表示系统完全解耦，因此能量解耦目标函数Fi(x)为

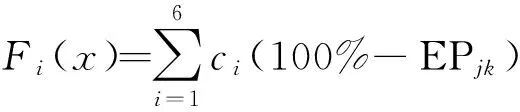
(5)

式中，ci为第i阶频率的加权因子.

利用Adams/View建立设计变量与目标函数，然后引入到Insight中，并设计一个试验.采用DOE Response Surface对试验结果进行Quadratic二次模型拟合，并利用D-Optimal有效地缩减设计矩阵，对灵敏度进行分析，然后优化求解动力总成悬置系统的刚度参数.

4.2动力总成悬置系统优化前后对比分析

通过对动力总成悬置系统进行优化求解，得到定阻尼条件下悬置系统刚度优化结果与之前结果对比如表3所示，表4、5为优化前后悬置系统的固有频率及解耦程度对比，表5中，X、Y、Z及R分别表示平动及转动方向.

表3　悬置元件刚度比较

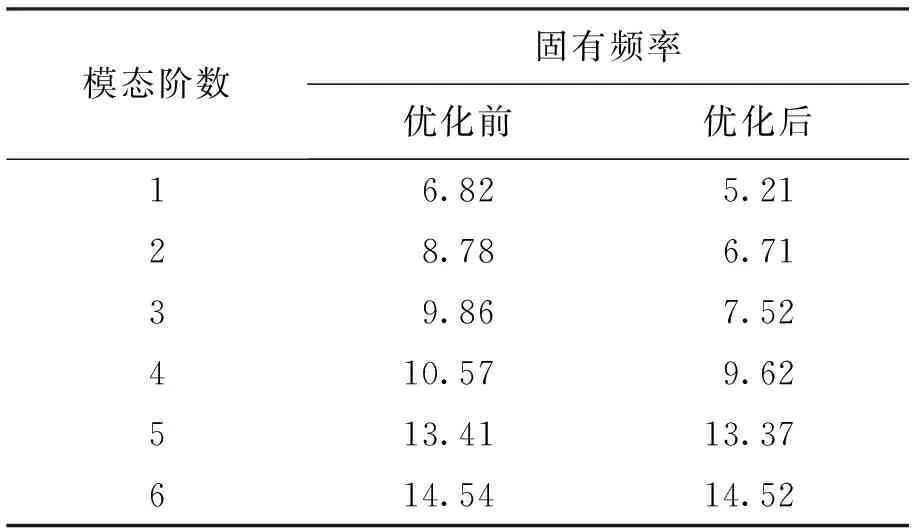
表4　悬置系统固有频率的比较

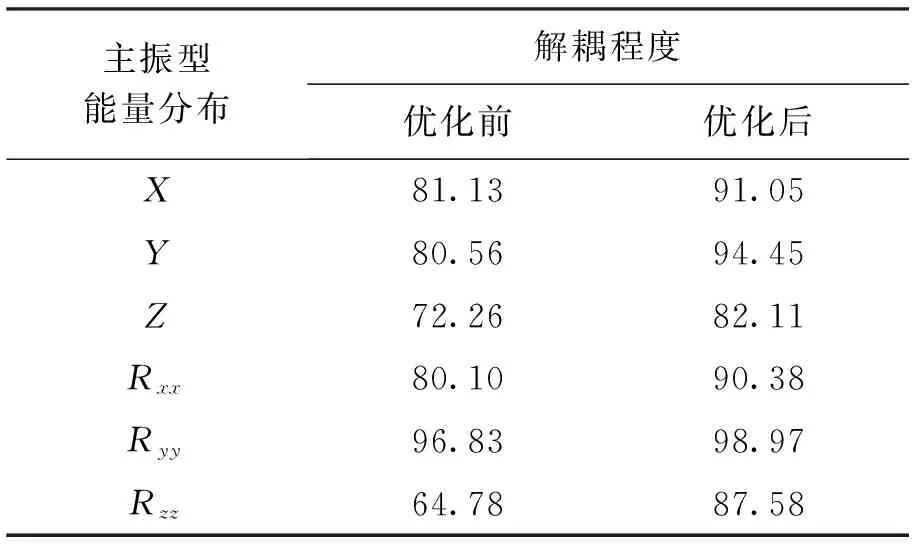
表5　悬置系统的解耦程度比较

从表3悬置刚度优化结果中可以看出，优化后X方向的刚度值普遍降低；Y方向上左前、左后悬置的刚度值有所增大，右前、右后悬置的刚度有所减小；Z方向上右前、左后悬置的刚度有所增大，左前、右后悬置的刚度有所减小，动力总成存在扭转振动现象，所以在讨论悬置刚度参数时要同时考虑每一个位置悬置刚度的变化规律.从表4中能够看出，优化前后悬置系统的6阶固有频率都小于16 Hz，避开了怠速时的共振频率；优化后悬置系统的固有频率有所降低，怠速工况时的共振问题能够很好地避免.通过表5比较优化前后的主振型能量分布情况发现，各阶模态上的主振型能量都有所提高，且除沿Z轴平动的振动能量分布是82.11%以外，其它各个自由度方向上的能量分布都超过了85%，振动耦合现象有了很大程度上的改善[11].

图11～14为系统在怠速工况下，有阻尼时优化后各悬置垂直方向支反力随时间变化的曲线.

通过优化后垂直方向支反力的响应曲线(图11～14)和优化前有阻尼情况(图4、6、8、10)对比分析发现，在怠速工况下，左前悬置垂直支反力稳定在1 500 N左右，其波动幅值由144 N减小为133 N；右前悬置垂直支反力稳定在1 390 N左右，其波动幅值由130 N减小为124 N；左后悬置垂直支反力稳定在230 N左右，其波动幅值由32 N减小为27 N；右后悬置垂直支反力稳定在220 N左右，其波动幅值由26 N减小为21 N.各悬置处的垂直支反力波动幅值普遍降低，减小了力的传递，减振效果有了很大改善.

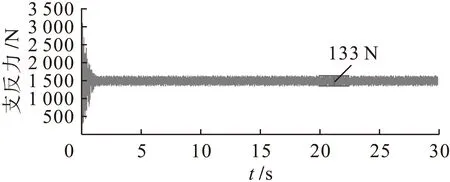
图11　优化后左前悬置支反力

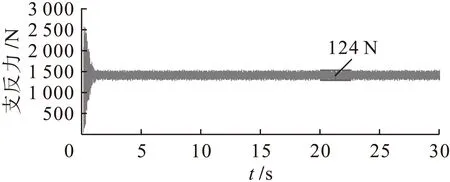
图12　优化后右前悬置支反力

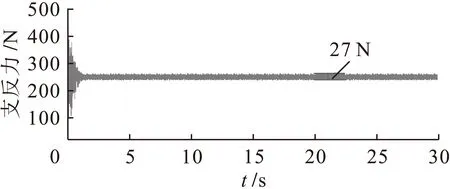
图13　优化后左后悬置支反力

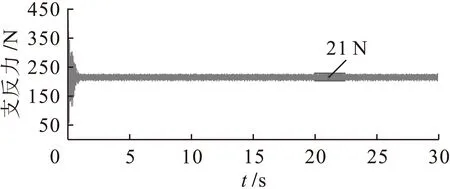
图14　优化后右后悬置支反力

图15为系统在怠速工况下，考虑阻尼时优化前后动力总成质心位移随时间变化的曲线.从图15可以看出，优化前动力总成的质心经过一段较大的波动后稳定在3.4 mm左右，优化后质心位移波动稳定在2.3 mm左右，质心的位移减小了很多，有效地降低了动力总成的振动幅值，悬置系统起到了减振的作用[12].

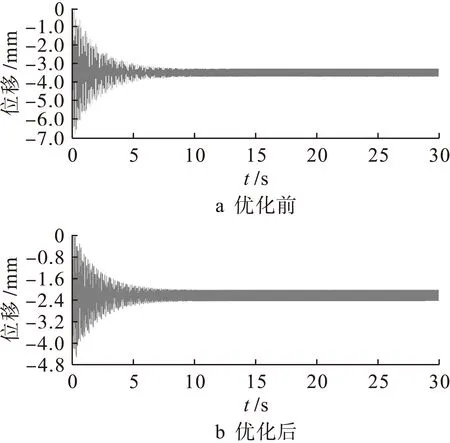
图15　优化前后动力总成质心位移

5　结　论

本文针对汽车普遍存在动力总成在怠速过程中的振动问题，对某型号动力总成及其悬置系统应用Adams/View构建了空间六自由度的动力学模型，利用Adams/Vibration模块分析得到了系统的固有频率，并就得到的问题借助Adams/Insight模块对系统进行了优化.优化后动力总成悬置系统左前、右前、左后、右后的垂直支反力波动幅值分别减小了7.6%、4.6%、15.6%、19.2%，动力总成的质心在平稳运行中的振动位移明显减小，降低了振动的传递，减小了动力总成悬置系统的振动，并且各阶固有频率值都有所降低，各阶次的解耦程度基本都达到了85%以上，有了明显提高.结果表明，采用以动力总成悬置系统在各阶固有频率主振方向上的能量解耦程度为目标函数，能很好地匹配悬置系统的参数，达到悬置系统的减振目的.

[1]Peter G，Klaus W，Kiran G，et al.NVH aspects of powertrain integration into the vehicle [J].MTZ Worldwide，2002，63(6)：14-17.

[2]张武，陈剑，高煜.基于粒子群算法的发动机悬置系统稳健优化设计 [J].农业机械学报，2010，41(5)：30-35.

(ZHANG Wu，CHEN Jian，GAO Yu.Robust optimal design of an engine mounting system based on particle swarm optimization [J].Transactions of the Chinese Society for Agricultural Machinery，2010，41(5)：30-35.)

[3]周洪威，李雪梅，刘夫云，等.叉车振动仿真及发动机总成悬置优化 [J].噪声与振动控制，2014，34(6)：65-70.

(ZHOU Hong-wei，LI Xue-mei，LIU Fu-yun，et al.Vibration simulation of a forklift truck and optimization of its engine mounting system [J].Noise and Vibration Control，2014，34(6)：65-70.)

[4]谢展，于德介，李蓉，等.基于区间分析的发动机悬置系统稳健优化设计 [J].汽车工程，2014，36(12)：1503-1507.

(XIE Zhan，YU De-jie，LI Rong，et al.Robust optimization design of engine mount systems based on interval analysis [J].Automotive Engineering，2014，36(12)：1503-1507.)

[5]张玉增，柴山，刚宪约，等.发动机悬置系统的研究综述 [J].农业装备与车辆工程，2012(1)：23-27.

(ZHANG Yu-zeng，CHAI Shan，GANG Xian-yue，et al.Study on engine mounting system [J].Agricultural Equipment & Vehicle Engineering，2012(1)：23-27.)

[6]Uys P E，Els P S，Thoresson M J.Suspension settings for optimal ride comfort of off-road vehicles travelling on roads with different roughness and speeds [J].Journal of Sound and Vibration，2004，275(3/4/5)：973-990.

[7]张子庆，倪计民，石秀勇，等.基于路面激励的动力总成受振特性分析及评价 [J].沈阳工业大学学报，2011，33(2)：159-165.

(ZHANG Zi-qing，NI Ji-min，SHI Xiu-yong，et al.Vibration characteristic analysis and evaluation of powertrain based on road excitation [J].Journal of Shen-yang University of Technology，2011，33(2)：159-165.)

[8]何洋志，陈吉清，兰凤崇.动力总成悬置系统隔振分析及优化 [J].现代制造工程，2012(2)：80-83.

(HE Yang-zhi，CHEN Ji-qing，LAN Feng-chong.Analysis and optimization of power assembly mounting vibration isolation [J].Modern Manufacturing Engineering，2012(2)：80-83.)

[9]陈克，吕品.汽车动力总成悬置系统隔振性能仿真方法 [J].中国机械工程，2014，25(20)：2830-2834.

(CHEN Ke，LÜ Pin.Simulation method for the vibration isolation performance of vehicle powertrain mounting system [J].China Mechanical Engineering，2014，25(20)：2830-2834.)

[10]李征，纪金亮，杨河洲，等.基于能量解耦的汽车动力总成悬置系统参数设计 [J].汽车科技，2011，7(4)：25-27.

(LI Zheng，JI Jin-liang，YANG He-zhou，et al.Para-meters design of vehicle powertrain mounts based on energy decoupling [J].Auto Mobile Science & Techno-logy，2011，7(4)：25-27.)

[11]何亚运，张代胜.基于能量解耦和传递路径分析的发动机悬置系统优化 [J].噪声与振动控制，2015，35(4)：65-70.

(HE Ya-yun，ZHANG Dai-sheng.Optimization of an engine mount system based on energy decoupling and transfer path analysis [J].Noise and Vibration Control，2015，35(4)：65-70.)

[12]Hu J F，Chen W W，Huang H.Decoupling analysis for a powertrain mounting system with a combination of hydraulic mounts [J].Chinese Journal of Mechanical Engineering，2013，26(4)：737-745.

(责任编辑：景勇英文审校：尹淑英)

Optimization and vibration reduction analysis for powertrain mounting system

CHEN Ke, LI Xiao-zheng, ZHOU Shuang-shuang

(School of Automobile and Transportation, Shenyang Ligong University, Shenyang 110159, China)

In order to solve the vibration isolation problem in the vehicle powertrain mounting system, the simulation model for a certain type of powertrain mounting system was established. For the mounting system with and without damping, the comparative analysis for the support reaction of mounting system was carried out. Through selecting 12 main direction stiffness of four rubber mounting systems as the design variable and the energy decoupling degree in the main vibration direction of each order natural frequency of powertrain mounting system as the objective function, the optimization of powertrain mounting system was performed with Adams/Insight module. The results show that the support reaction of optimized mounting system obviously reduces, and the transmission of powertrain vibration also decreases. Moreover, the decoupling degree gets obviously enhanced, and the vibration reduction effect of mounting system gets greatly improved.

powertrain; mounting system; vibration; stiffness; damping; support reaction; Adams/Insight module; energy decoupling; optimization design

2015-04-29.

辽宁省教育厅科学研究资助项目(L2012068).

陈克(1965-)，男，辽宁沈阳人，教授，博士，主要从事汽车动力学与控制等方面的研究.

10.7688/j.issn.1000-1646.2016.01.10

TB 123

A

1000-1646(2016)01-0057-06

*本文已于2015-12-07 16∶18在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20151207.1618.036.html