基于有限元仿真的形状记忆聚合物弓丝初始正畸力分析

仵健磊 刘云峰* 彭 伟 林文武 徐立新

1(浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州 310014)2(浙江工业大学材料科学与工程学院，杭州 310014)

基于有限元仿真的形状记忆聚合物弓丝初始正畸力分析

仵健磊1刘云峰1*彭 伟1林文武1徐立新2

1(浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州 310014)2(浙江工业大学材料科学与工程学院，杭州 310014)

正畸治疗过程中，临床常用镍钛金属弓丝对人体存在潜在的毒性作用，且缺乏美观性；相比之下形状记忆聚合物(SMP)材料因其良好的力学性能、易成形、美观性，在正畸中受到越来越多的重视。而形状记忆聚氨酯(SMPU)作为一种典型的SMP材料，其在正畸治疗效果方面的研究尚不充分，所能提供的矫治力大小有待进一步探究。在正畸矫治力研究中，临床口内检测非常困难，有限元分析技术是目前最主要的研究手段。针对上述问题，基于Tobushi一维SMP本构方程，参照粘弹性材料标准线性模型构建了SMP材料的三维本构方程，并利用FORTRAN语言编写了可用ABAQUS调用的UMAT子程序；参照正畸临床数据，利用三维建模软件建立了包括牙齿、托槽、弓丝在内的三维有限元模型，以侧切牙、尖牙为研究对象，通过对弓丝施加不同形式的变形，得出SMPU弓丝形变量为3 mm时产生的初始正畸力大小为0.06～0.55 N。结果表明， SMPU弓丝提供的初始正畸力与临床认为的最佳正畸力相比略为偏小，适合正畸治疗的第一阶段；但SMPU材料的力学性能还有进一步提升改善的空间，在正畸领域具有较高的潜在应用价值。

正畸力；形状记忆聚合物(SMP)；有限元；弓丝

引言

目前，正畸治疗过程中矫治器多采用金属弓丝矫治器，其中以镍钛弓丝矫治器最为常见。镍钛弓丝相比于其他金属弓丝具有很好的力学性能及生物相容性，且具有形状记忆功能，可以达到很好的治疗效果。然而，有研究表明镍钛合金中的镍元素在人体口腔复杂的环境下会发生腐蚀，释放有毒的镍离子，从而对人体产生毒性作用[1]，这引起了医生和患者的广泛关注；另一方面，金属弓丝由于不透明，难以满足人们在口腔正畸时对美学方面越来越高的要求。

为此，有学者提出将形状记忆聚合物(shape memory polymer,SMP)材料应用于弓丝，比如形状记忆聚氨酯(shape memory poly are thane, SMPU)[2]，其具有良好的力学性能[3]及生物相容性[4-5]，很容易通过注塑模、挤压等方式获得所需要的特殊形状[6]，并且SMP为无色透明材料，具有很好的美学效应。但SMP作为一种新型聚合物材料，其正畸治疗过程中所能提供的正畸力大小尚不明确。Yong等针对SMP材料在正畸领域的应用进行了相关的实验研究[2]，主要方式为基础材料实验和蜡模测试，实验中的不确定因素较多，SMP弓丝形变所能产生的正畸力尚需要进一步考证。在正畸矫治力研究中，口内检测非常困难，有限元分析技术是目前最主要的研究手段，为此本研究利用有限元的方法通过仿真正畸治疗过程中SMPU弓丝的变形，检测SMPU弓丝产生的初始正畸力，为临床治疗提供理论参考。

为探究新型SMPU弓丝在正畸过程中提供的初始正畸力大小，构建了包括上颌牙齿、托槽、弓丝在内的正畸有限元模型，并在Tobushi等在一维本构方程的基础上，建立了SMP材料的三维本构方程[7-8]。以上颌侧切牙、尖牙为研究对象，通过对弓丝施加不同形式的变形，分析在上颌侧切牙和尖牙存在唇舌向水平方向错位以及存在唇舌向与牙根冠向交叉方向错位时，SMPU弓丝由于形变所产生的初始正畸力。

1 材料和方法

1.1 SMPU的材料特性及本构模型

SMPU是一种典型的SMP材料，SMP材料的主要特性是具有形状记忆功能，即具有一定原始形态的SMP材料制品，在一定条件下改变其原始形态并固定之后，通过外界环境(如热、 电、光、化学感应等)的刺激又可以恢复其原始形态。SMPU属于热塑性形状记忆聚合物，其形状记忆功能主要受外界温度的影响，当外界温度达到其转变温度时，就会产生形状回复，其主要由硬质相(4,4-methylene bis)和软质相(poly(ε-caprolactone)diol)构成，通过改变其硬质相和软质相的比例，可以获得不同玻璃化转变温度的SMPU材料。研究中选用日本DIAPLEX公司型号为MM3520的SMPU材料，其玻璃化转变温度为35℃，与人体口腔温度相一致。

SMP材料的研究主要针对其材料的实验观察和新型应用上，关于SMP材料的热力学本构模型方面的研究尚不充分。为了更加准确地描述SMP材料的热力学特性，在Tobushi等一维本构方程的基础上，构建出了SMP材料的三维本构方程[9]，有

(1)

(2)

(3)

经验证，依据SMP材料三维本构方程的仿真结果与Tobushi等实验结果相一致。

在式(3)中，有

(4)

式中：σij(t)，εij(t)分别表示应力和应变；δij表示克罗内克符号(若i=j，δij=1，否则δij=0)，i,j=1,2,3；εkk表示体积应变，k=1,2,3；E表示弹性模量；μ表示黏度；λ表示延迟时间；K表示体积弹性模量；α表示热膨胀系数；T表示温度；εc表示蠕变应变；εL表示残余应变；C表示比例系数；εs表示残余蠕变应变；t表示时间。

ABAQUS作为功能强大的有限元分析软件，为用户提供了强大且灵活的用户子程序接口(user subroutine)和应用程序接口(utility sunroutine)，允许用户自行定义求解模型。用户材料子程序(UMAT)是ABAQUS提供用户自定义材料属性的FORTRAN程序接口，为用户解决一些非线性材料提供了很大的灵活性。利用FORTRAN语言，将式(3)进行编程，即得到SMP本构模型的UMAT子程序。

1.2 三维有限元模型的建立

1.2.1 上颌牙齿模型的建立

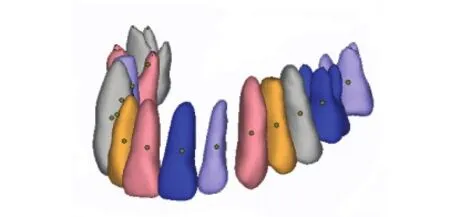
图1 上颌牙列几何模型Fig.1 Geometrical model of maxillary teeth

1.2.2 托槽模型的建立

托槽选取目前常用的自锁托槽，其尺寸参考直丝弓矫治器MBT托槽。托槽槽沟的高度H=0.56 mm，槽沟深度D=0.72 mm，且上颌不同牙位上的托槽上预置了不同的轴倾角、转矩角且有不同的托槽底形态与厚度。托槽的具体参数如表1所示。

表1 MBT托槽参数

自锁托槽结构比较复杂，为利于有限元分析进行了相应的简化。考虑到托槽的刚度、强度远远大于SMPU弓丝，故托槽的形变忽略不计，将托槽设置为刚体，托槽的单元类型采用R3D4R。当在ABAQUS/STANDARD中使用单纯的主-从接触算法模拟刚性表面的接触时，在接触相互作用中，刚性表面总是主控表面，故将托槽的表面设置为主控表面，SMPU弓丝的表面设置为从面。在有限元分析中，刚性表面必须足够大以保证从属节点不会滑出该表面和落到其背面，否则将会导致求解不收敛，为此将自锁托槽与弓丝的所有可能接触的表面进行相应的延伸，如图2所示，除非分析中发生穿透，否则该延伸面不参与接触。

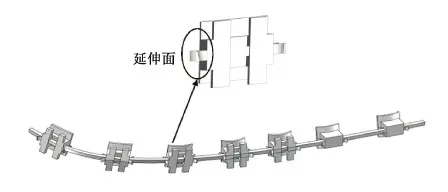
图2 自锁托槽几何模型Fig.2 Geometrical model of brackets

1.2.3 弓丝几何模型的建立

在正畸临床治疗过程中，弓丝的形态设计与应用对正畸治疗的效果有着重要的影响。根据对牙弓形态学的研究，学者提出了如幂函数模型、β函数模型、多项式模型、悬链线方程模型、抛物线方程模型和椭圆方程模型等牙弓形状量化数学模型[10-11]。采用比较符合中国人牙弓形状的幂函数模型[12]，幂函数牙弓模型[13]可表示为

(5)

式中，ρ与φ为模型的特征参数，有下面的拟合公式

(6)

式中：S、W、L分别表示半侧牙弓的弧长、宽度和高度；a、b和τ为拟合常数，且有a=10.889，b=0.88，τ=3。

如图3所示，根据幂函数模型建立了PU弓丝的数学模型，并利用三维建模软件UG建立了幂函数牙弓几何模型；如图4所示，弓丝为截面尺寸0.508 mm×0.762 mm的方形。

图3 弓丝数学模型Fig.3 Mathematical model of arch wire

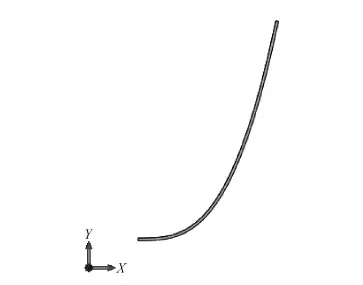
图4 弓丝几何模型Fig.4 Geometrical model of arch wire

SMPU弓丝形状规则，为精确计算采用单元形状六面体的实体单元，单元类型采用C3D8R，其材料特性参照构建出的SMP材料三维本构方程，本构方程的调用通过ABAQUS可供用户自定义的UMAT子程序。有限元中所用的SMPU弓丝材料参数由实验测得，具体参数如表2所示。其中，在玻璃化温度Tg下，Eg代表弹性模量，μg代表黏度系数，λg代表延迟时间，α代表热膨胀系数，Cg代表比例系数，εLg代表残余应变。SMPU弓丝只有在口腔环境(35℃)下，达到其玻璃化转变温度时才会产生形状回复，从而驱动牙齿移动，为此，主要在口腔温度下对SMPU弓丝进行有限元仿真，分析其由形变产生的初始正畸力。

表2 SMPU弓丝在Tg(35℃)时材料参数

Tab.2 Material parameters of SMPU arch wire inTg(35℃)

Eg/MPaμg/(GPa·s)λg/sα/K-1CgεLg/%15 462341 7265 1511 6×10-50 1120 3

1.3 有限元模型的约束设定

由于重点研究SMPU弓丝因形变产生的初始正畸力，并不考虑由于弓丝长期作用引起牙槽骨吸收重建的牙齿矫治过程，故本模型中不包含牙槽骨与牙周膜等组织。为了简化分析，假设上颌左右两边对称，取上颌牙列模型的一半作为研究对象，弓丝的近中端设置为对称约束。同时为使SMPU弓丝在模型装配过程中不产生预应力，参照标准形态弓丝对上颌牙列进行修正排齐，且所有托槽的中心位于同一平面上，如图5所示。

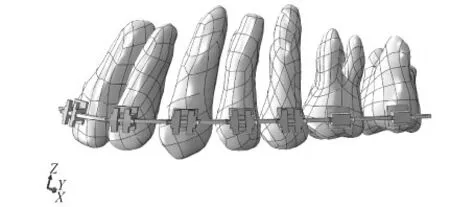
图5 正畸几何模型Fig.5 Orthodontic geometrical model

在有限元分析过程中，弓丝与托槽的接触状态会不断地发生变化，为简化有限元分析，增加模型的收敛性和可计算度，简化了弓丝与托槽之间的接触设置，对需要移动的的托槽与弓丝之间设置为绑定接触，其余托槽与弓丝之间的接触形式为有限滑动接触。另外，考虑到弓丝与托槽之间的摩擦力主要影响正畸治疗过程中由于牙齿移动而引起的托槽与弓丝的相对滑动，而对弓丝变形所产生的初始正畸力影响很小，故在仿真时设置弓丝与托槽之间为光滑无摩擦接触。

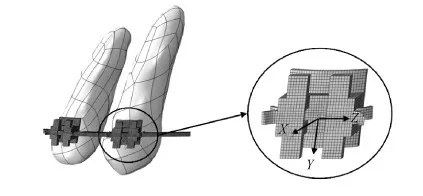
图6 托槽的局部坐标系Fig.6 Local coordinate system of brackets

1.4 弓丝形变的控制形式

2 结果

2.1 唇舌向错位的有限元分析

正畸有限元分析过程中，分别对22牙位侧切牙和23牙位尖牙沿X轴正方向和负方向施加3 mm的位移量，得到有限元模型的应力云图如图7所示。通过后处理可以获得牙齿位移与SMPU弓丝产生的初始正畸力的关系曲线，如图8所示。从图8中的四条牙齿位移与初始正畸力的关系曲线，可以看出SMPU弓丝的正畸力与牙齿位移量整体成正相关。22牙位切牙沿X轴正向(唇侧)位移量由0逐步增加到3 mm期间，正畸力随着牙齿位移量基本成线性增加，在位移量为3 mm时达到最大值，约为0.55 N；23牙位尖牙沿X轴正向(唇侧)移动时位移与正畸力曲线基本与22牙位切牙相似，相比于22牙位其斜率较小，位移量由0增加到3 mm过程中的最大正畸力为0.25 N；22牙位切牙沿X轴负向(舌侧)移动时，位移量与正畸力关系曲线与沿X轴正向(唇侧)移动时不同，在0～1.5 mm初级阶段正畸力基本随位移量的增加而增加，当位移量达到1.5 mm之后，正畸力则不再随其继续增加，在位移量达到2.5 mm时反而有下降的趋势，在位移量由0变化到3 mm时，正畸力在1.5～2.5 mm处达到最大值，为0.06 N；23牙位尖牙沿X轴负向(舌侧)移动时的位移量与正畸力曲线仍基本符合线性关系，正畸力随着位移量的增加而逐步增大，在位移量为1.7 mm时，关系曲线发生转折，斜率变大，牙齿移动过程中，最大正畸力出现在位移3 mm处，大小为0.18 N。由以上分析可以得知，牙齿沿唇舌向由0逐渐移动3 mm时，SMPU弓丝所能提供的最大正畸力大小为0.06～0.55 N。

图7 唇舌向牙齿错位有限元应力云图。(a)侧切牙沿X轴正方向移动3 mm；(b)尖牙沿X轴正方向移动3 mm；(c)侧切牙沿X轴负方向移动3 mm；(d)尖牙沿X轴负方向移动3 mmFig.7 Finite element stress nephogram when dislocation occur in ligula direction. (a)Lateral incisor move 3 mm along positive direction of X axis; (b)Canine tooth move 3 mm along positive direction of X axis; (c)Lateral incisor move 3 mm along negative direction of X axis; (d)Canine tooth move 3 mm along negative direction of X axis

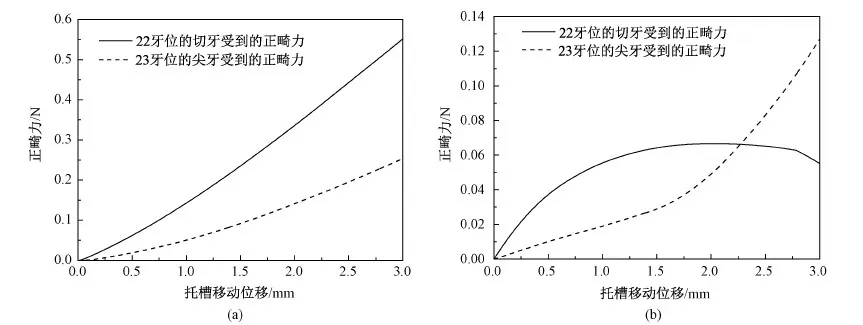
图8 牙齿沿唇舌向移动时位移与初始正畸力关系曲线。(a)牙齿沿X轴正方向(唇侧)移动时位移与初始正畸力关系曲线；(b)牙齿沿X轴负方向(舌侧)移动时位移与初始正畸力关系曲线Fig.8 Related curve between displacement and initial orthodontic force when teeth move along ligula direction. (a)Related curve between displacement and initial orthodontic force when teeth move along positive direction of X axis；(b)Related curve between displacement and initial orthodontic force when teeth move along negative direction of X axis

图9 交叉方向牙齿错位时的应力云图。(a)侧切牙沿X轴正向与Y轴负向夹角45°方向移动2.82 mm；(b)尖牙沿X轴正向与Y轴负向夹角45°方向移动2.82 mm；(c)侧切牙沿X轴正向与Y轴正向夹角45°方向移动2.82 mm；(d)尖牙沿X轴正向与Y轴正向夹角45°方向移动2.82 mmFig.9 Finite element stress nephogram when dislocation occur in crossed direction. (a)Lateral incisor move 2.82 mm along 45° angular direction of positive X axis and negative Y axis; (b)Canine tooth move 2.82 mm along 45° angular direction of positive X axis and negative Y axis; (c)Lateral incisor move 2.82 mm along 45° angular direction of positive X axis and positive Y axis; (d)Canine tooth move 2.82 mm along 45° angular direction of positive X axis and positive Y axis

图10 牙齿沿交叉方向移动时位移与初始正畸力关系曲线。(a)牙齿沿X轴正向与Y轴负向夹角45°方向移动时位移与初始正畸力关系曲线；(b)牙齿沿X轴正向与Y轴正向夹角45°方向移动时位移与初始正畸力关系曲线Fig.10 Related curve between displacement and initial orthodontic force when teeth move along crossed direction. (a) Related curve between displacement and initial orthodontic force when teeth move along 45° angular direction of positive X axis and negative Y axis；(b)Related curve between displacement and initial orthodontic force when teeth move along 45° angular direction of positive X axis and positive Y axis

2.2 唇舌向伴随牙根冠方向错位的有限元分析

临床正畸中，牙齿的错位不仅仅发生在唇舌向，往往伴随着牙根冠方向的错位。在有限元仿真过程中，同样选取侧切牙和尖牙为研究对象，分别对22牙位侧切牙和23牙位尖牙沿X轴正向与Y轴负向呈45°角方向移动2.82 mm，以及沿X轴正向与Y轴正向呈45°角方向移动2.82 mm，得到牙齿沿交叉方向移动时的有限元模型的应力云图，如图9所示。经后处理得到牙齿沿交叉方向移动时位移与初始正畸力关系曲线，如图10所示。由其位移与正畸力关系曲线可以看出，22牙位切牙和23牙位尖牙沿交叉方向移动时，其位移量与正畸力关系曲线仍基本符合线性关系，如图10(a)所示，牙齿沿X轴正向与Y轴负向夹角45°方向移动时，其正畸力随位移量呈线性增加，22牙位切牙的关系曲线斜率要大于23牙位尖牙的曲线斜率，在位移量为2.82 mm时正畸力达到最大值，其中22牙位切牙为0.5 N，23牙位尖牙为0.26 N；如图10(b)所示，22牙位切牙沿X轴正向与Y轴正向夹角45°方向移动时，正畸力在位移量为0.7～1.5 mm处出现一个平台，随后正畸力又随着位移量的增加而线性增加，在2.82 mm处达到最大值0.11 N；23牙位尖牙沿X轴正向与Y轴正向夹角45°方向移动的位移量与正畸力关系曲线同样成线性关系，在位移量为2.82 mm时，正畸力大小为0.18 N。可以看出，牙齿沿交叉方向移动3 mm时，SMPU弓丝所能提供的最大正畸力范围在0.11～0.5 N。

3 讨论

由牙齿唇舌向错位时有限元分析结果图8可知，牙齿沿唇侧向移动时相比于沿舌侧向移动时产生的初始正畸力更大，主要是由于为了简化分析，假设上颌左右两边牙齿对称的前提条件下，取上颌一半的模型作为研究对象，并且对该边界施加对称约束，因此弓丝不存在沿对称面的法向移动，而在托槽移动过程中，会引起弓丝长度变化，弓丝产生弯曲变形的同时，伴随着一定的轴向变形，因此托槽向唇侧移动时的正畸力比向舌侧的大，这也说明施加一定的轴向拉伸变形会增加弓丝的正畸力。另外，侧切牙沿舌侧方向移动时，所产生的正畸力并没有一直随着牙齿位移的增加而增加，这主要是由于侧切牙处的曲率半径较大，侧切牙向舌侧移动时伴随着弓丝在托槽内的滑动引起的，从结果中可以看出，对弓丝末端施加相应的固位约束，也可以提高弓丝的正畸力。牙齿沿唇舌向移动时产生的最小初始正畸力为0.06 N，最大初始正畸力为0.55 N。

与牙齿沿唇舌向移动时的位移与初始正畸力的关系曲线相似，牙齿沿交叉向移动时得到的位移与正畸力关系曲线仍整体呈线性关系。另外，可以看出牙齿沿唇侧偏牙根45°方向移动时，正畸力相比于牙齿沿舌侧偏牙冠45°方向更大，这主要是因为牙齿沿唇侧偏牙根45°方向移动时引起了弓丝更大的轴向拉伸。牙齿沿交叉方向移动时得到的最小初始正畸力为0.11 N，最大初始正畸力为0.53 N。

比较牙齿沿唇侧方向移动与牙齿沿唇侧偏牙根45°方向移动的位移与正畸力关系曲线，可以看出虽然牙齿沿着不同的方向移动，但得到的位移与正畸力关系曲线基本一致，说明牙齿同样沿弓丝外法线方向移动时，在小角度的范围内，不会对弓丝的正畸力产生太大的影响，其正畸力主要与牙齿位移大小相关。所以，在临床正畸治疗中，同样沿牙弓外法线方向但错位形式不同的牙齿，其在矫治过程中所需要的正畸力只与牙齿的偏移量相关，而与牙齿的偏移方向无关。

由以上讨论分析，在定义托槽与弓丝的接触形式为光滑无摩擦前提下，得出SMPU弓丝在变形量为3 mm(交叉移动方式下为2.82 mm)时初始正畸力大小范围为：0.06～0.55 N。临床治疗过程中认为最佳正畸力的范围在0.98～1.47 N之间[14]，所以SMPU弓丝相比于金属弓丝所能提供的正畸力是偏小的，在实际临床应用中可以对SMPU弓丝实施一定的预紧力，从而提高其正畸治疗过程中的正畸力。另外，有研究表明在牙齿矫治的第一阶段(排齐牙列)正畸治疗效果不依赖弓丝产生的正畸力大小，较柔和的正畸力同样可以达到很好的治疗效果[15]，因此SMPU弓丝可以应用在正畸治疗中的第一阶段。

4 结论

为了更加准确描述SMP材料的热力学特性，在Tobushi等一维本构方程的基础上，构建了SMP材料的三维本构方程；参照人体实际口腔数据建立了包括牙齿、托槽、弓丝在内的正畸有限元模型，以牙齿错位量为3 mm(交叉移动方式下为2.82 mm)为例，分析了上颌侧切牙和尖牙在不同错位方式下SMPU弓丝产生的正畸力，其大小为0.06～0.55 N，该力与临床治疗最佳正畸力(0.98 ～1.47 N)相比略为偏小，比较适合正畸治疗中的第一阶段(排齐牙列)。在临床应用中也可以通过对SMPU弓丝施加一定的预紧，从而提高其治疗过程中正畸力。

SMP材料由于其良好的生物相容性和美观性，在生物医学领域正受到越来越多的重视，在正畸领域具有很高的潜在应用价值。由于SMP材料可以添加增强剂等改性方法改善其力学性能，未来将继续对SMP弓丝材料进行深入研究，包括对新型SMP材料的探索以及现有SMP材料的改性，希望获得与现有金属弓丝性能相近的SMP弓丝。

[1] Aziz-Kerro M, Conroy KG, Fenelon AM, et al. Electrochemical studies on the stability and corrosion resistance of titanium-based implants materials [J]. Biomaterials, 2001, 22(12): 1531-1539.

[2] Jung YC, Cho JW. Application of shape memory polyurethane in orthodontic [J]. Journal of Material Science: Material Medicine, 2010, 21(10): 2881-2886.

[3] Ghosh P, Srinivasa AR. A two-network thermomechanical model of a shape memory polymer [J], International Journal of Engineering Science, 2011, 49(9): 823-838.

[4] Mccabe JF, Yan Z, Alnaimi OT, et al. Smart materials in dentistry-future prospect [J]. Dental Material Journal, 2009, 28(1): 37-43.

[5] Andreas L, Marc B, Bernhard H, et al. Shape-memory polymers as a technology platform for biomedical applications [J]. Expert Review of Medical Devices, 2010, 7(3): 357-379.

[6] Sun Li, Huang Weimin, Ding Zheng, et al. Stimulus-responsive shape memory materials: a review [J]. Materials and Design, 2012, 33: 577-640.

[7] Tobushi H, Hashimoto T, Hayashi S, et al. Thermomechanical constitutive modeling in shape memory polymer of polyurethane series [J]. Intelligent Material Systems and Structures, 1997, 8: 711-718.

[8] Tobushi H, Okumura K, Hayashi S, et al. Thermomechanical constitutive model of shape memory polymer [J]. Mechanics of Materials, 2001, 33: 545-554.

[9] 章巧芳，林文武，张钦，等. 热驱动形状记忆聚合物三维力学本构模型 [J]. 浙江工业大学学报, 2015, 43(1): 43-46.

[10] 张林，段沛沛，陈杨熙. 正畸弓丝形态的研究发展 [J]. 国际口腔医学杂志, 2012, 39(2): 273-276.

[11] 蒋济雄. 口腔正畸弓丝成形规划及弯制机器人研究 [D]. 哈尔滨: 哈尔滨理工大学, 2013.

[12] Zhang Yongde, Jiang Jingang, Lv Peijun, et al. Study on the multi-manipulator tooth-arrangement robot for complete denture manufacturing [J]. Industrial Robot: an International Journal, 2011, 38(1): 20-26.

[13] 吕培军，李国珍. 用数学构成法对牙弓、颌弓几何形态的研究 [J]. 中华口腔医学杂志, 1989, 34(2): 76-78.

[14] 钱英莉，樊瑜波，蒋文涛. 正畸力作用下牙齿移动的生物力学 [J]. 医用生物力学, 2003, 18(3): 189-192.

[15] Varela JC, Velo M, Espinar E, et al. Mechanical properties of a new thermoplastic polymer orthodontic archwire [J]. Materials Science and Engineering C, 2014, 42: 1-6.

[16] Ni Qingqing, Zhang Chunsheng, Fu Yaqin, et al. Shape memory effact and mechanical properties of carbon nanotube/shape memory polymer nanocomposites [J]. Composite Structures, 2007, 81(2): 176-184.

[17] Shahrul AA, Aidah J, Nik AR, et al. Determination of shape fixity and shape recovery rate of carbon nanotube-filled shape memory polymer nanocomposites [J]. Procedia Engineering, 2012, 41: 1641-1646.

[18] Byoung CC, Mi HC, Yong-Chan C. Effect of glycerol cross-linking and hard segment content on the shape memory property of polyurethane block copolymer [J]. Journal of Material Science, 2007, 42: 6524-6531.

Initial Orthodontic Force Analysis of Shape Memory Polymer Arch Wire Based on Finite Element Simulation

Wu Jianlei1Liu Yunfeng1*Peng Wei1Lin Wenwu1Xu Lixin2

1(KeyLaboratoryofE&M(ZhejiangUniversityofTechnology),MinistryofEducation&ZhejiangProvince，Hangzhou310014,China)2(CollegeofMaterialsScienceandEngineering,ZhejiangUniversityofTechnology,Hangzhou310014,China)

In orthodontic treatment, metallic arch wire may produce potential toxic effect to human and can not satisfy the aesthetic requirements. In contrast, shape memory polymer (SMP) arch wire has attracted more and more attention for its good mechanical properties and aesthetic appearance. However, shape memory polyurethane (SMPU) as a typical kind of material, its effect in orthodontic treatment, including the force supplied by SMPU wire still remains to be explored. In orthodontic research, the intra-oral evaluation of the force supplied by appliances is difficult to achieve, and finite element method (FEM) has been widely applied as an alternative method. Aiming at these problems, based on the one-dimensional SMP constitutive equation built by Tobushi, a 3D constitutive equation of SMP is derived reference to the standard model of viscoelastic material, and user-defined material mechanical behavior (UMAT) subroutine used for ABAQUS is written by FORTRAN language. From clinical orthodontics data, a 3D model including teeth, brackets and SMPU arch wire were constructed. Taking a maxillary lateral incisor and a canine as examples, through exerting different deformation on arch wire, the initial orthodontic force of arch wire was acquired by FEM simulation. When deflection is 3 mm, the value range is 0.06～0.55N. The results revealed that the initial orthodontic force of SMPU arch wire is somewhat smaller than the optimal orthodontic force required in clinic, and is suitable in the first phase of orthodontic treatment. But the mechanics performances of SMP are still needed to be improved, which will promote a very high potential value on medical application in the future.

orthodontic force；shape memory polymer(SMP); finite element; arch wire

10.3969/j.issn.0258-8021. 2016. 02.011

2015-06-20， 录用日期:2015-12-23

国家自然科学基金(51375453)；浙江省自然科学基金(LY13E050017)

R318

A

0258-8021(2016) 02-0202-09

*通信作者(Corresponding author)， E-mail: liuyf76@126.com