浸渍涂覆过程中液膜流动的数值模拟
2016-09-15陈蒙蒙张先明陈文兴冯连芳
陈蒙蒙,张先明,陈文兴,冯连芳
(1.浙江理工大学纺织纤维材料与加工技术国家地方联合工程实验室,杭州 310018;2.浙江大学,a.化学工程国家重点实验室;b.化学工程与物工程学系,杭州 310027)
浸渍涂覆过程中液膜流动的数值模拟
陈蒙蒙1,张先明1,陈文兴1,冯连芳2a,b
(1.浙江理工大学纺织纤维材料与加工技术国家地方联合工程实验室,杭州 310018;2.浙江大学,a.化学工程国家重点实验室;b.化学工程与物工程学系,杭州 310027)
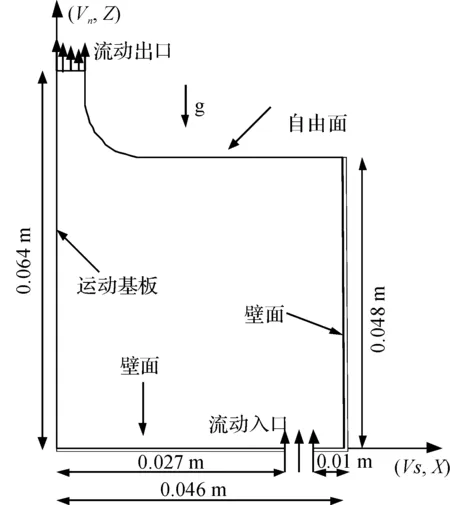
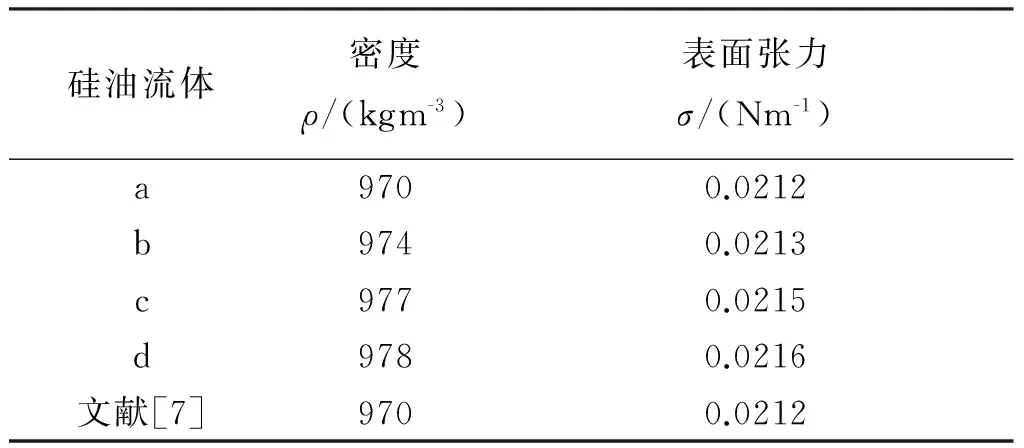
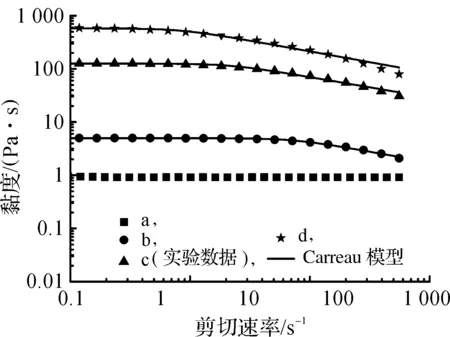
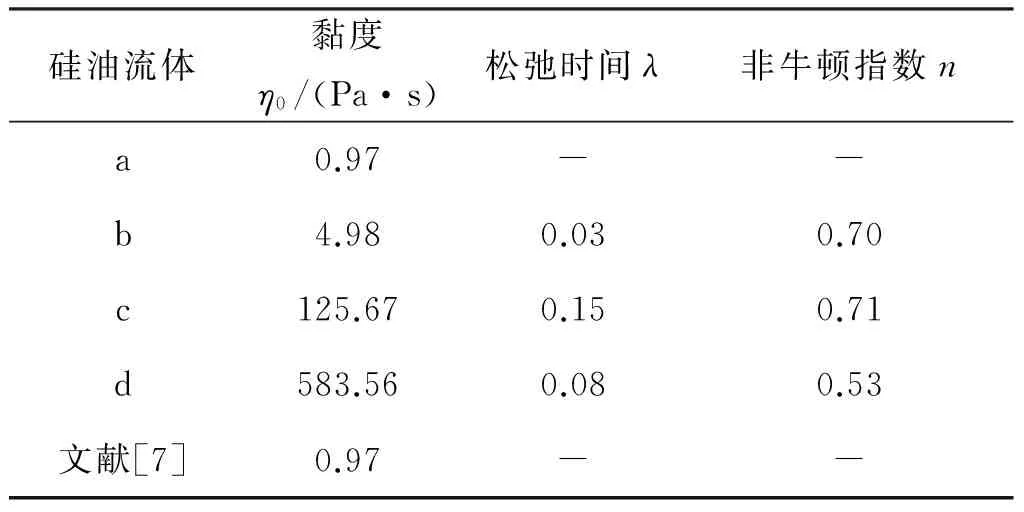
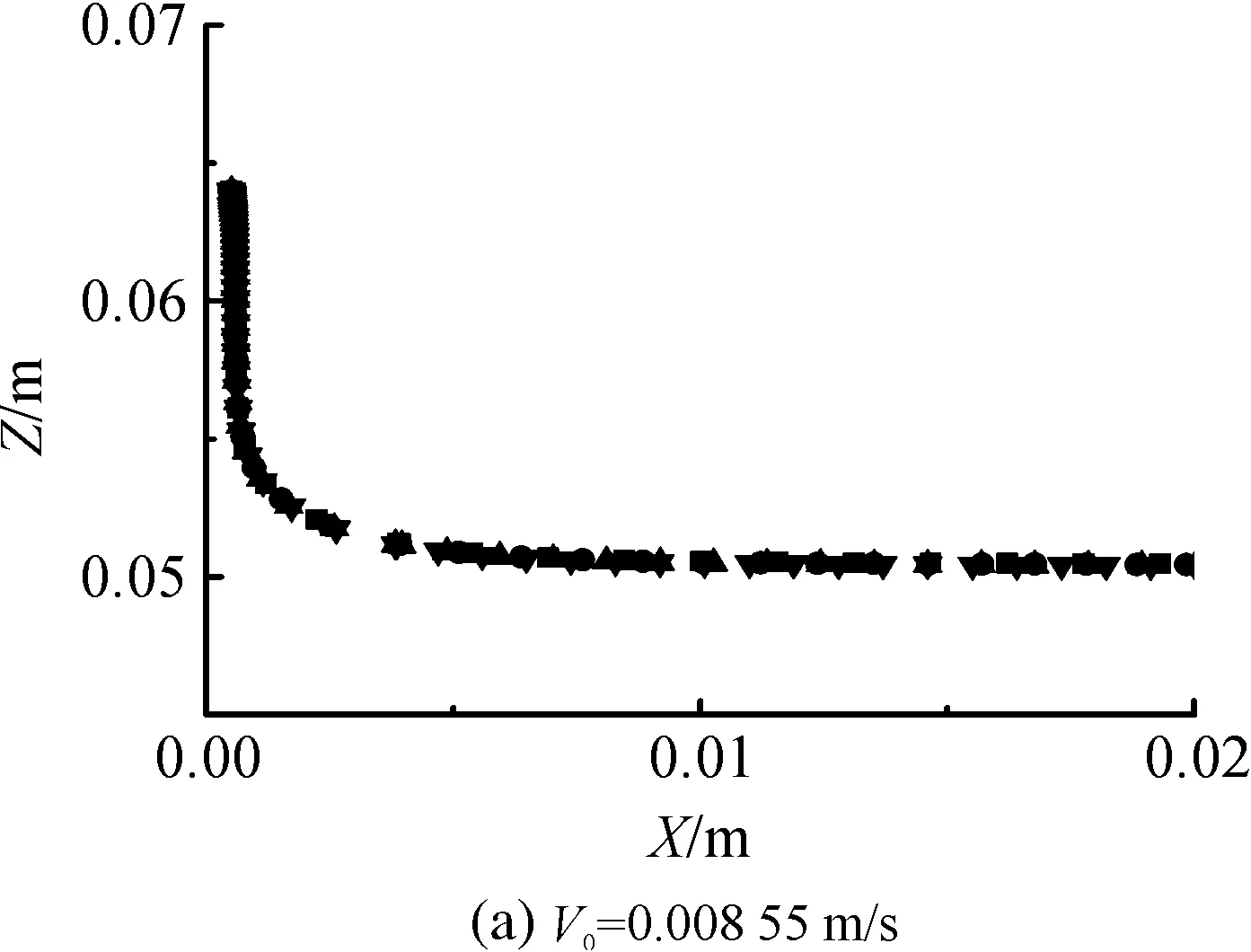
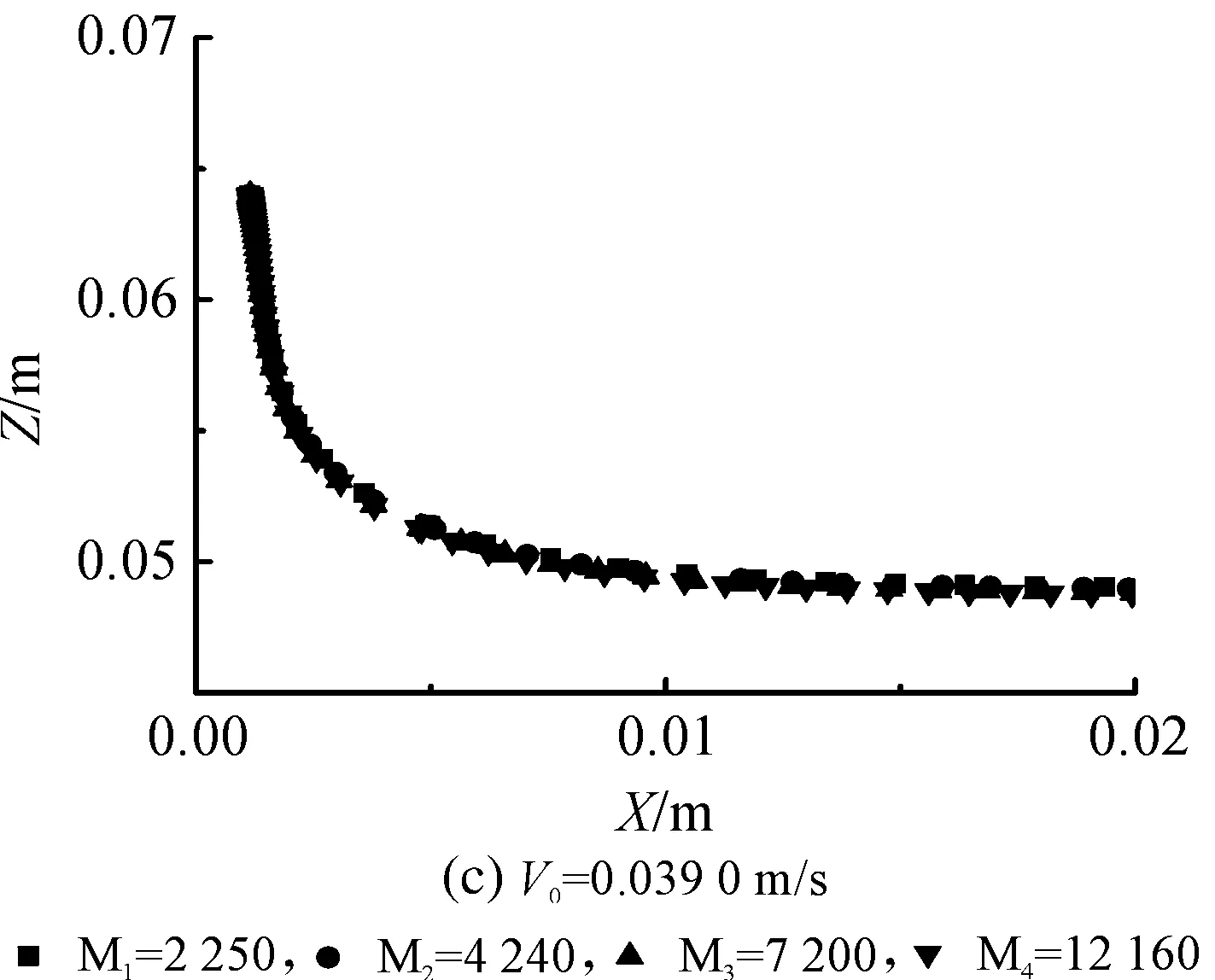
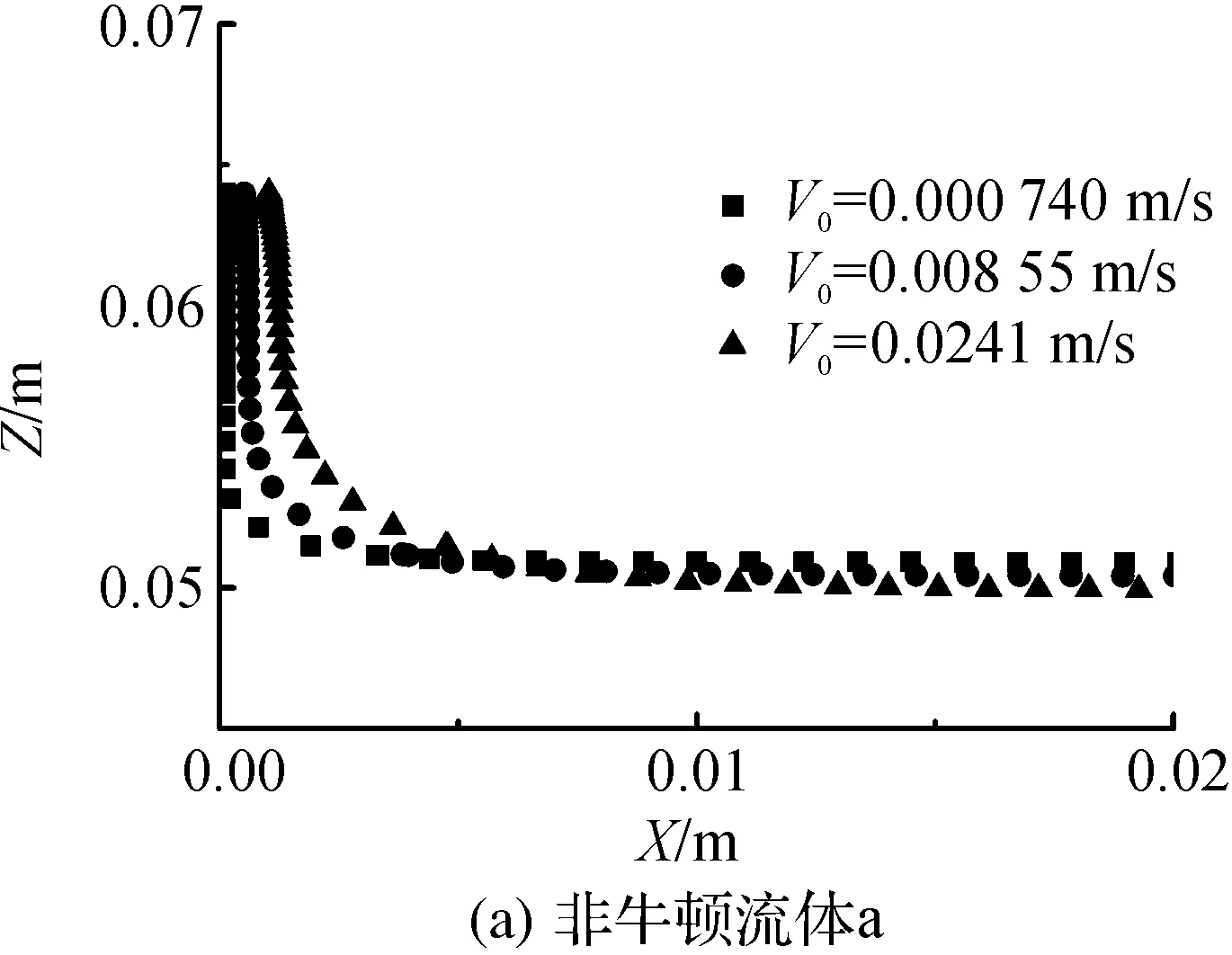
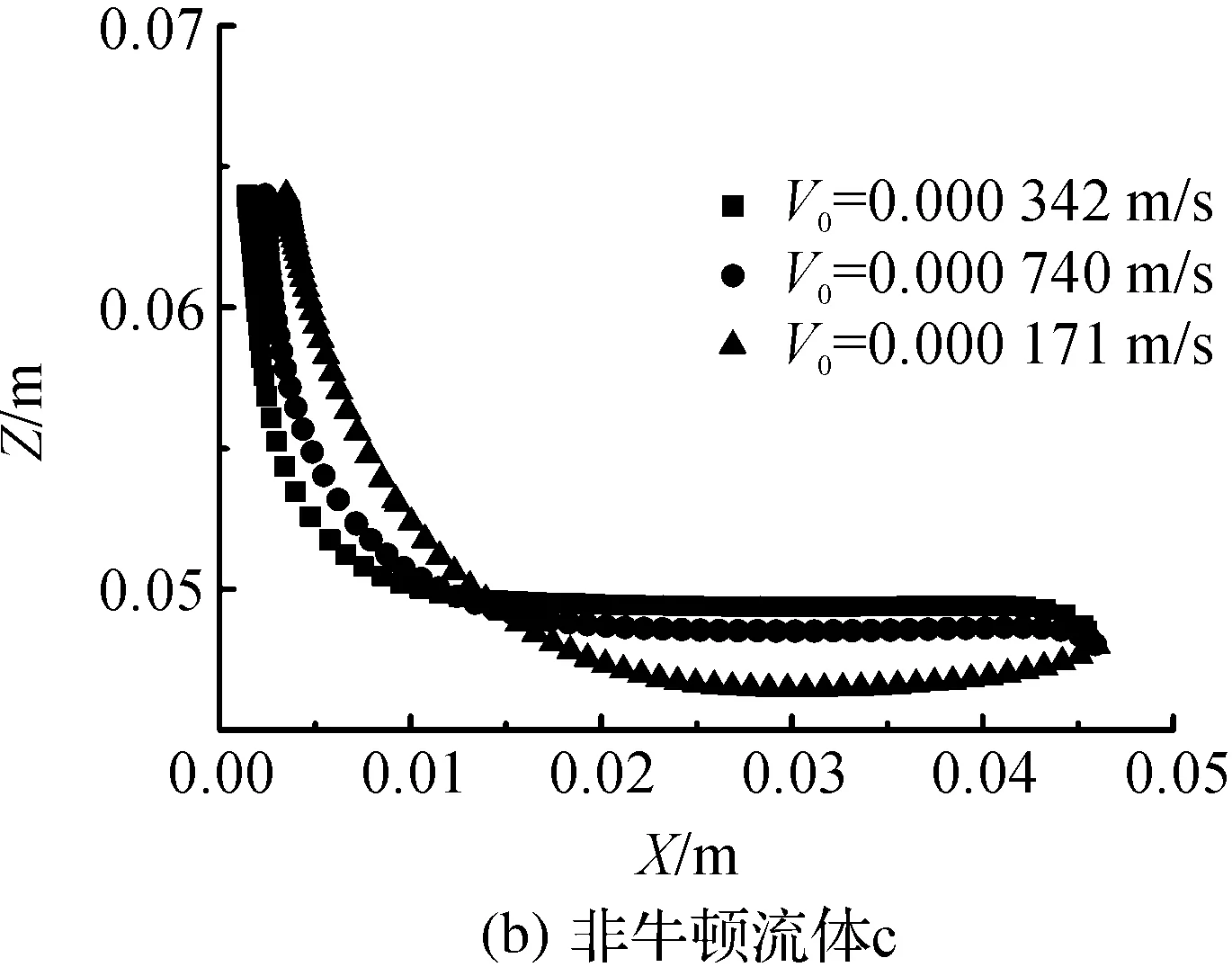
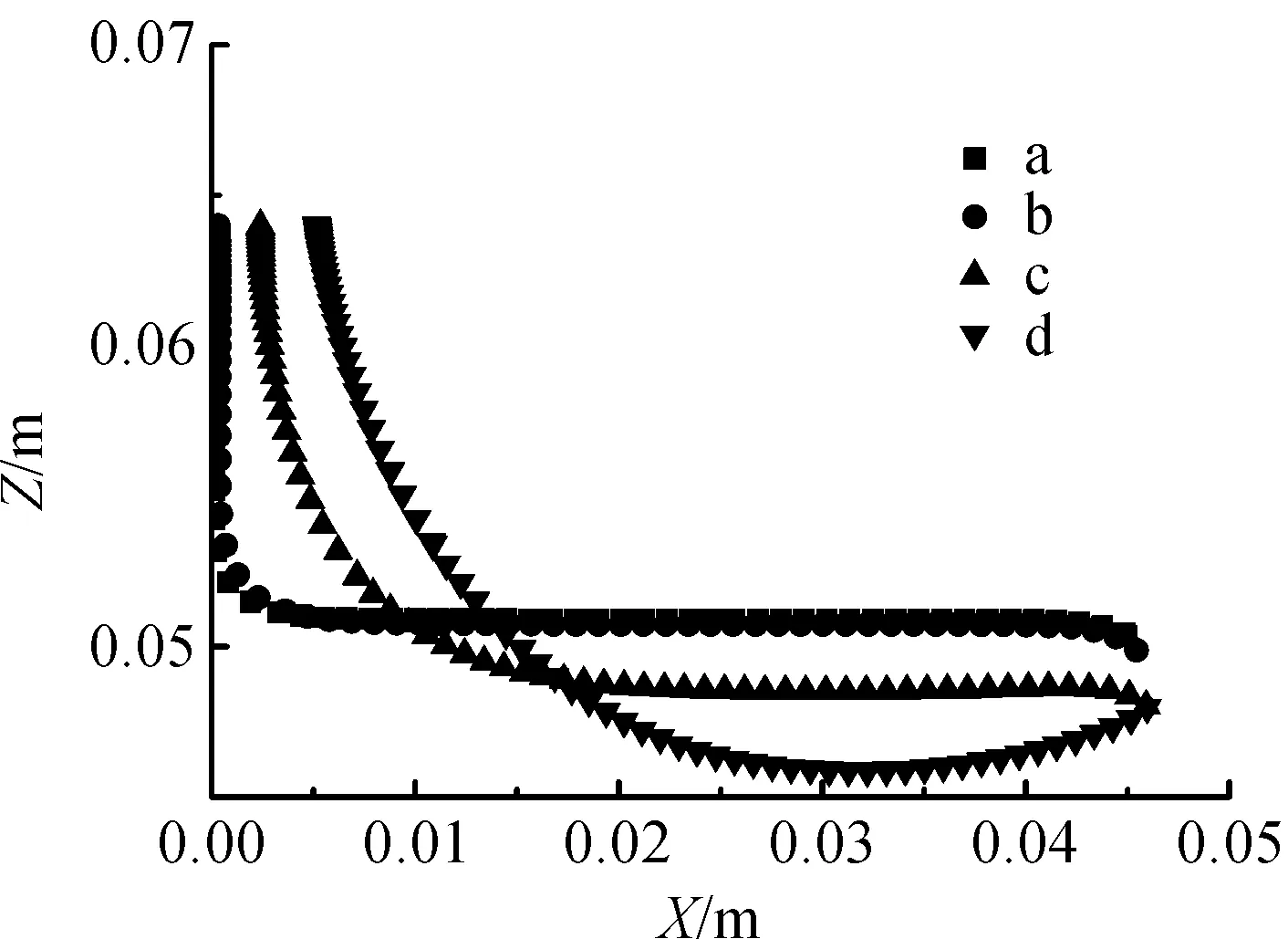
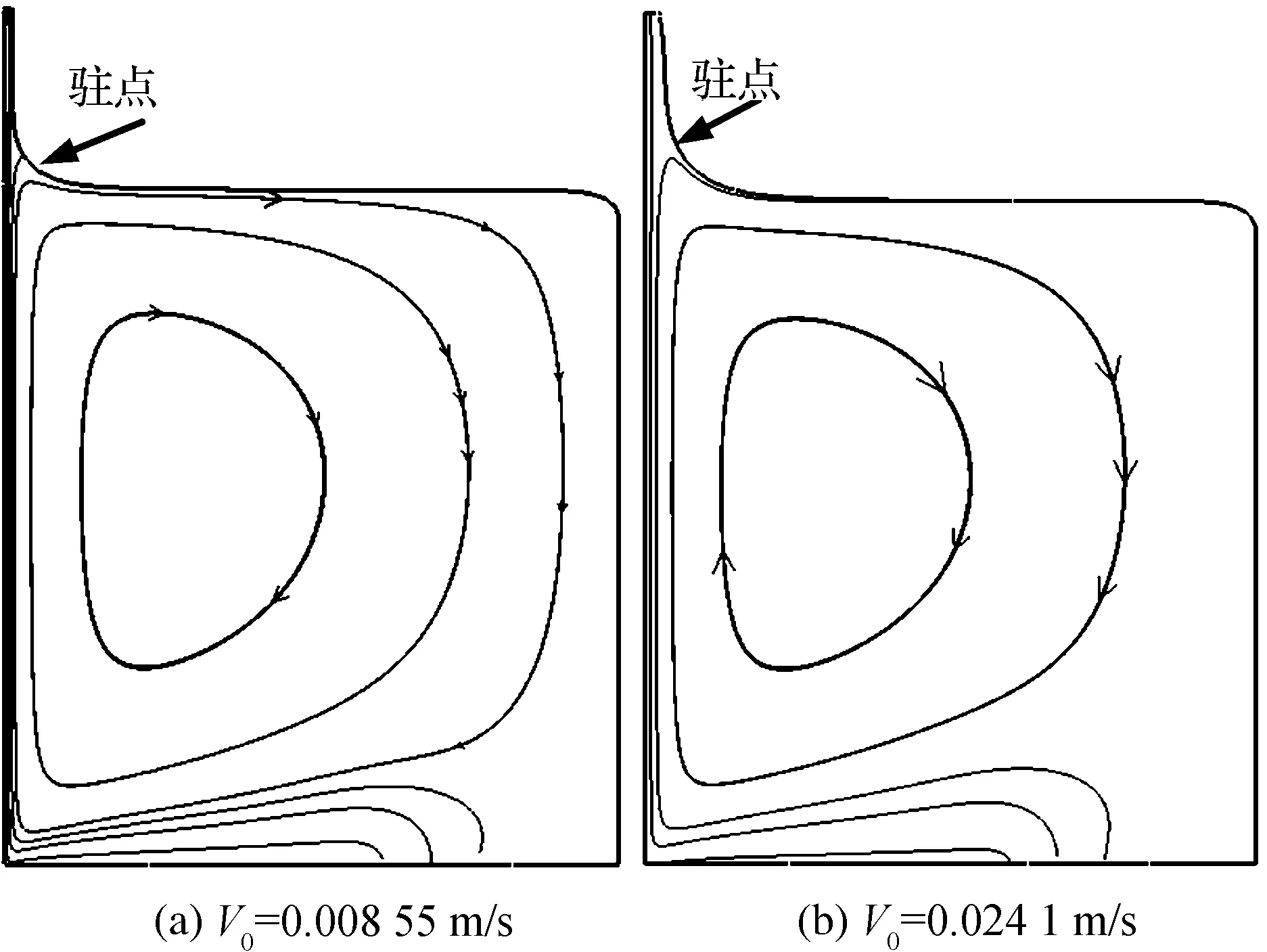
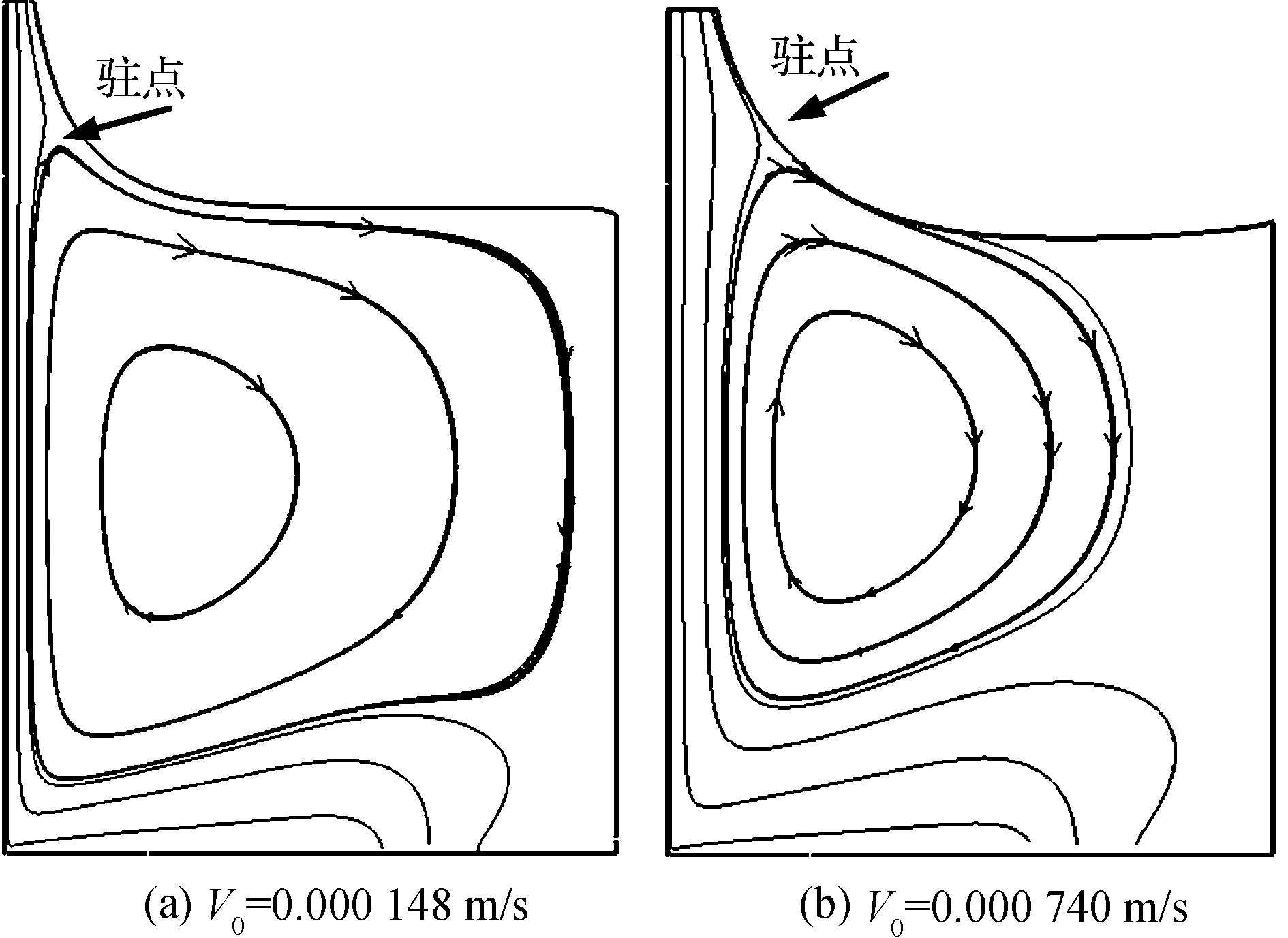
结合有限元法和网格重划分法,在毛细数(Ca)0.01 浸渍涂覆;液膜流动;数值模拟 浸渍涂覆过程是将洁净干燥的基材浸入到预先准备好的流体中,然后将其以一定的速度平稳地向上提拉,在黏性力、惯性力、表面张力和重力共同作用下,在基材表面附着一层均匀的液膜,经过干燥固化后得到均匀的膜产品的过程。浸渍膜通常用作装饰、保护膜和功能材料(如镀锌钢、磁信息储存材料和半导体组件)等[1]。 浸渍涂覆过程由于流体复杂黏弹特性、自由面演化和工艺参数影响,因此有着非常复杂的动力学行为。本文在0.01 1.1物理模型 图1是浸渍涂覆过程的示意,其中基板以一定的速度V0垂直向上提拉,液槽宽0.046 m,深0.064 m,初始液位在0.048 m处,而且是静止的。流体在惯性力、黏性力、表面张力和重力作用下处于稳定涂覆过程。为了补偿沿基板向上运动的流体,在液槽底部设置流体入口,使液位与初始液位相差小于20%。整个模拟过程均是在室温条件下进行的。 图1 浸渍涂覆过程示意 1.2流体物性 模拟流体为聚二甲基硅氧烷(蓝星化工新材料股份有限公司江西星火有机硅厂),其稳定性好,具有很高的抗剪切能力,可在-50~200 ℃下长期使用,其物理性质见表1。 表1 硅油流体的物理性质 注:a、b、c和d指4种性质不同的流体。 4种流体的流变曲线均在室温下通过Physica MCR 301型旋转式流变仪(Anton Paar GmbH)测得,其中硅油流体b、c和d的流变曲线符合Carreau模型,其拟合结果如图2所示,拟合参数见表2。对于流体a来说,随剪切速率的增大,其黏度不变,因此其为牛顿流体。图2显示,流体b、c、d,当剪切速率较小时,其黏度变化不大,而当剪切速率较大时,其黏度随剪切速率的增大而减小,这种流体的黏度受其剪切行为的影响很大,表现出明显的假塑性行为,因此是非牛顿流体。 图2 4种硅油流体的流变曲线 硅油流体黏度η0/(Pa·s)松弛时间λ非牛顿指数na0.97--b4.980.030.70c125.670.150.71d583.560.080.53文献[7]0.97-- 1.3数学模型 硅油流体具有一定的黏度和密度,且自由面上的空气可认为是无黏性的,压力为0,所以薄膜流动可看作不可压缩层流流动,其质量和动量守恒方程如下: Δ·u=0 (1) (2) 其中:u为速度矢量,p为压力,F为表面张力。 在等温条件下,牛顿流体的黏度为恒定值。 η=η0 (3) 非牛顿流体的黏度随剪切速率的变化用Carreau模型来描述: (4) 1.4边界条件 为了求解控制方程,必须对边界施加合理的边界条件:在固液交界面处,流体速率等于固体表面速率,所以假设流体粘在固体上,即无滑移条件;流动入口流率根据Wilson[8]建立的公式求得;当存在表面张力时,求解自由面时需在其起始点指定初始条件;假设流动出口处的膜厚已经达到平衡状态,其速度分布根据Hurez等[5]建立的公式求得。 1.5数值方法 由于非牛顿流体的流变行为复杂,且流动过程中自由面的形状和位置未知,因此不易进行数值计算。以Polyflow为求解器,利用FEM-Remeshing法来追踪自由面可克服这个问题。当存在表面张力效应时,采用二次坐标、二次速度的形函数插值方法以得到准确的结果,并采用Picard迭代法来提高计算的收敛性;时间步进算法采用隐式欧拉法;由于提拉过程中自由面网格变形比较复杂,所以在整个计算域选择Thompson转化法作为网格重划分方法。 2.1网格单元数量的选择 当基板从流体中以一定速度V0垂直向上提拉时,自由面上的一部分网格会因自由面的变化而受到影响,所以需要重新划分网格,根据边界上节点位置的变化重新定义内部的节点。为了说明网格单元数量对模拟结果的影响,在不同提拉速度时用4种不同数量的网格单元M1、M2、M3和M4来分别计算牛顿流体a的自由面,如图3(a)-(c)所示。图3可见,各自由面彼此重合,说明所选网格单元对计算结果影响较小。当V0较小时,膜厚较小,基板附近的网格需进一步细化来描述该区域内流体单元的运动,同时考虑到增加网格密度会大大增加计算内存,降低计算速度,所以为了在准确描述流体单元运动的前提下尽量减小计算内存,本文中网格单元数量选择M3。 图3 不同提拉速度时,网格数量对牛顿流体a的自由面的影响 2.2牛顿流体膜厚的模拟结果与实验结果的对比 图4 Kizito等[7]实验和本模拟的无量纲膜厚T0与Ca的关系 2.3提拉速度和黏度对自由面和膜厚的影响 图5 模拟流体的V0对其自由面的影响 图6是V0=0.000740 m/s时4种流体自由面的变化。由于同一提拉速度时,随流体黏度的增大,运动时相邻两层流体间的内摩擦剪切应力增大,使更多的流体沿运动基板向上运动,所以动态弯月区内自由面的曲率减小,而膜厚大大增加。 图6 V0=0.000740 m/s时,流体黏度对其自由面的影响 2.4流场分布 图7中显示了牛顿流体a在不同提拉速度时流动过程的流线图。图7可见,整个流场明显分为两个区域:在流场的上部,基板邻近的流体沿基板向上运动,而下部的流体远离基板返回液槽中,并在流体内部形成一个漩涡,在自由面上形成一个驻点,且随V0的增大,驻点沿自由面逐渐远离基板运动,与Landan等[2]的实验研究结果一致。黏度较小的非牛顿流体b的流场有相似的变化。 图7 牛顿流体a的提拉速度对其流线图的影响 非牛顿流体d在不同提拉速度时的流线图如图8所示,当提拉速度V0较小时,驻点在流体内部而不是在自由面上形成,随着V0的增大,驻点逐渐远离基板,同时流体内部的漩涡逐渐减小。黏度较大的非牛顿流体c的流场有相似的变化。 图8 非牛顿流体d的提拉速度对其流线图的影响 本文在合适的条件下,利用FEM-Remeshing法成功地模拟了硅油流体在浸渍涂覆过程中自由面和膜厚的变化,随着提拉速度或黏度的增大,动态弯月区内自由面的曲率减小,而膜厚增加,并且牛顿流体膜厚的模拟结果与Kizito等的实验结果相差小于20%。对提拉过程中流场的分析结果表明:黏度较小的牛顿流体a和非牛顿流体b的流场稳定后,整个流场明显可分为两个区域:在流场的上部,基板邻近的流体沿着基板向上运动,而下部的流体远离基板流回槽中,在其内部形成一个漩涡,在自由面上形成一个驻点,且随V0的增大,驻点沿自由面远离基板运动。而黏度较大的非牛顿流体c和d的驻点首先在流体内部形成,随V0的增大,远离基板,同时流体内部的漩涡逐渐减小。 [1] KISTLER S F, SCHWEIZER P M. Liquid Film Coating [M]. London: Chapman &Hall, 1997: 1-15. [2] LANDAU L D, LEVICH B V. Dragging of a liquid by a moving plate [J]. Acta Physicochim, USSR, 1942, 17: 42-54. [3] MAYER H C, KRECHETNIKOV R. Landau-Levich flow visualization: Revealing the flow topology responsible for the film thickening phenomena [J]. Physics of Fluids, 2012, 24(5): 1-33. [4] KRECHETNIKOV R, HOMSY G M. Experimental study of substrate roughness and surfactant effects on the Landau-Levich law [J]. Physics of Fluids, 2005, 17(10): 1-16. [5] HUREZ P, TANGUY P. Finite element analysis of dip coating with Bingham fluids [J]. Polymer Engineering and Science, 1990, 30(18): 1125-1132. [6] FILALI A, KHEZZAR L, MITSOULIS F. Some experiences with the numerical simulation of Newtonian and Bingham fluids in dip coating [J]. Physics of Fluids, 2013, 82: 110-121. [7] KIZITO J P, KAMOTANI Y, OSTRACH S. Experimental free coating flows at high capillary and Reynolds number [J]. Experiments in Fluids, 1999, 27(3): 235-243. [8] WILSON S D R. The drag-out problem in film coating theory [J]. Journal of Engineering Mathematics, 1982, 16(3): 209-221. (责任编辑: 张祖尧) Numerical Simulation of Liquid Film Flow in Dip Coating Process CHENMengmeng1,ZHANGXianming1,CHENWenxing1,FENGLianfang2a,b (1. National Engineering Laboratory for Textile Fiber Materials and Processing Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2a. Key Laboratory of Chemical Engineering; 2b.Department of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, China) Finite element method (FEM) was combined with remeshing method to simulate the film flow problem in dip coating for silicone oil fluids in the range of capillary numbers 0.01 dip coating; liquid film flow; numerical simulation 10.3969/j.issn.1673-3851.2016.01.008 2015-04-14 国家973前期研究专项(2014CB660801) 陈蒙蒙(1989- ),女,河南商丘人,硕士研究生,主要从事浸渍涂覆数值模拟方面的研究。 张先明,E-mail:zhangxm@zstu.edu.cn O357.1 A 1673- 3851 (2016) 01- 0047- 05 引用页码: 0102050 引 言
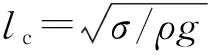
1 实验部分
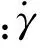
2 结果与讨论

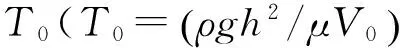


3 结 论
