Grötzsch环函数的几个不等式
2016-09-15马晓艳屠国燕
马晓艳,屠国燕
(1.浙江理工大学理学院,杭州 310018;2.同济大学浙江学院,浙江 嘉兴 314051)
Grötzsch环函数的几个不等式
马晓艳1,屠国燕2
(1.浙江理工大学理学院,杭州 310018;2.同济大学浙江学院,浙江 嘉兴 314051)
建立了Ramanujan模方程中Grötzsch环函数μ(r)与第二类完全椭圆积分ε(r)及拟共形理论中的Hübner函数m(r)之间的关系,并通过研究μ(r)与某些初等函数及特殊函数组合的单调性,获得了μ(r)的几个不等式,利用这些结果给出了μ(r)+logr的上下界,从而改进了已知的此类估计,同时给出了μ(r)形如Landen恒等式的不等式形式。所得结果有助于研究Ramanujan模方程理论。
Gauss超几何函数;Grötzsch环函数;Ramanujan模方程;不等式
0 引 言
对于实数a,b,c(c≠0,-1,-2,…),Gauss超几何函数定义为:
F(a,b;c;x)=2F1(a,b;c;x)
(1)
其中:当a≠0时,(a,0)=1;而当n=1,2,…时,
(a,n)=a(a+1)(a+2)(a+3)…(a+n-1)
(2)
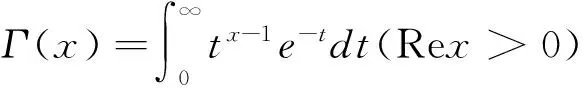
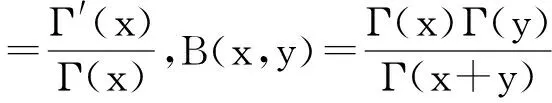
(3)
R(a,b)=-Ψ(a)-Ψ(b)-2γ,
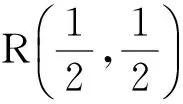
(4)
γ是Euler-mascheroni常数。
超几何函数在几何函数论、数论等数学分支中有着重要的作用,作为Gauss超几何函数的特殊情况,Legendre第一类、第二类完全椭圆积分为:

(5)
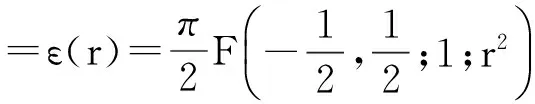
(6)
κ(r)满足Landen恒等式:
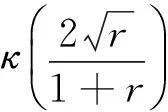
(7)
用B2表示平面上单位圆盘,μ(r)表示平面Grötzsch极值环B2[0,r](0 (8) 函数μ(r)在拟共形和拟正则理论中具有特殊重要性[1-2],它在解析函数论和数论等数学分支也有不少应用。 对任意的r∈(0,1),符号差为2的p(>1)次经典模方程[3]即为下面的方程: (9) 利用函数μ(r)可将方程(9)及其解(称为奇异值)s依次表示为: μ(s)=pμ(r)和s=φ1/p(r) (10) 其中φK(r)=μ-1(μ(r)/K)为Hersch-Pfluger偏差函数[1],因此可借助于μ(r)和φK(r)的性质来研究方程(10)及其解s。 由Landen恒等式(7)及定义(8),可得到模函数μ(r)的恒等式(参见文献[4]中5.2节): (11) 受这些恒等式的启发,本文通过研究拟共形映照理论中平面Grötzsch环μ(r)与特殊函数及某些初等函数的组合函数的单调性,获得了μ(r)满足的一些不等式,所得结果有助于进一步研究Ramanujan模方程理论。 (12) max{μ(r)-log2,Cμ(r)} (13) (14) 为了证明结论,需要用到下面几个公式及几个引理(参见文献[5]中定理4.1(1)-(5),式9和式1.11)。 引理3即为单调性洛比达法则(MonotoneI′Hpital′sRule),引自文献[4]中定理1.25;引理4引自文献[6]中定理2.4和2.5(4);引理5揭示了第一类、第二类完全椭圆积分的分析性质。结果如下: 的单调性也是如此。如果函数f′(x)/g′(x)的单调性是严格的,那么F和G的单调性也是严格的。 (15) (16) (17) 因此,由引理3、式(6)以及文献[5]中引理5.4(1),即可得到f的单调性。另外,利用I′Hpital法则可以得到以及f(1-)=0。 定理1的证明。 (18) 由引理3及引理5知,函数F单调递减。 根据I′Hpital法则,极限F(1-)=0可以得到。 (19) 由引理3及引理5,函数G单调递增。根据I′Hpital法则,可得极限值G(0+)=2/π。 定理2的证明。 (20) (21) (22) 便可以得到不等式(13)。 (23) 本文通过研究Grötzsch环函数μ(r)与第二类完全椭圆积分ε(r)及拟共形理论中的Hübner函数m(r)组合的单调性质,获得了数论中Ramanujan经典模方程中超几何函数比的一些不等式,改进了已有的结果,同时通过研究Grötzsch环函数μ(r)的分析性质,获得了μ(r)形如Landen恒等式的不等式形式,这些结果可用于Ramanujan经典模方程的进一步研究。 [1] QIU S L, VUORINEN M. Handbook of Complex Analysis: Special Function in Geometric Function Theory[M]. Elsevier B V, 2005: 621-659. [2] ANDERSON G D, VAMANAMURTHY M K. Rotation of plane quasiconformal mappings[J]. Thoku Math J, 1971, 23(2): 605-620. [3] BERNDT B C, BHARGAVA S, GARVAN F G. Ramanujan’s theories of elliptic functions to alternative bases[J]. Trans Amer Math Soc, 1995, 347: 4163-4244. [4] ANDERSON G D,VAMANAMURTHY M K, VUORINEN M. Conformal Invariants, Inequalities, and Quasiconformal Mappings [M]. New York: John Wiley & Sons,1997: 32-47. [5] ANDERSON G D, QIU S L, VAMANAMURTHY M K, et al. Generalized elliptic integrals and modular equations[J]. Pacific J Math, 2000, 192(1): 1-37. [6] 王淼坤,褚玉明,蒋月评,等. 零平衡超几何函数的一类二次变换不等式[J]. 数学物理学报, 2014, 34(A): 999-1007. (责任编辑: 康锋) Some Inequalities for Grötzsch Ring Function MAXiaoyan1,TUGuoyan2 (1. School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China;2. Tongji Zhejiang College, Jiaxing 314051, China) This paper establishes the relationship among the Grötzsch ring function μ(r), the complete elliptic integrals of the second kind ε(r) and the Hübner function m(r) in Ramanujan modular equation. By studying the monotonicity properties of μ(r) and some combinations of elementary functions and special funcitons, several inequalities are gained. The upper and lower boundaries of μ(r)+log (r) are given according to these results. Thus, known estimation is improved. Meanwhile, inequality form of μ(r) such as Landen identical equation is given. All results contribute to studying the theory of Ramanujan modular equation. Gaussian hypergeometric function; Grötzsch ring function; Ramanujan’s modular equation; inequality 10.3969/j.issn.1673-3851.2016.01.021 2015-02-06 国家自然科学基金项目(11171307);浙江省教育厅科研项目(Y201328799) 马晓艳(1979-),女,吉林梅河口人,副教授,主要从事Ramanujan模方程、特殊函数方面的研究。 O174 A 1673- 3851 (2016) 01- 0129- 04 引用页码: 010801
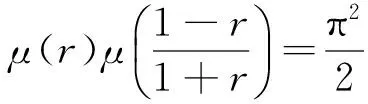
1 主要结果
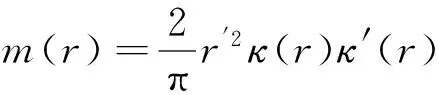

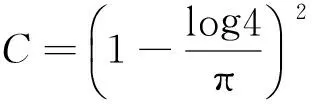
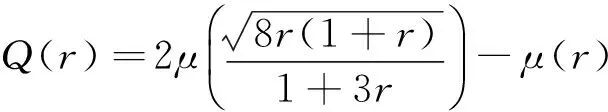
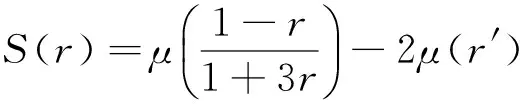
2 引 理

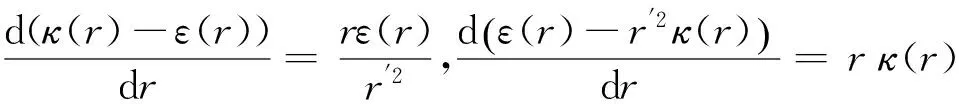
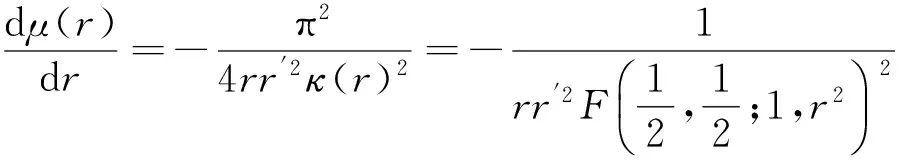
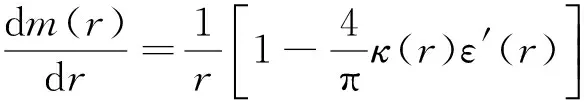
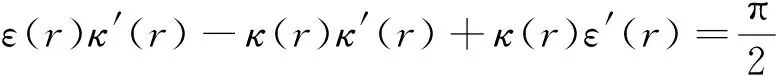
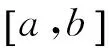
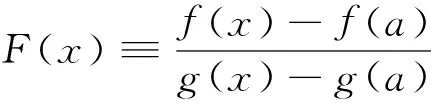

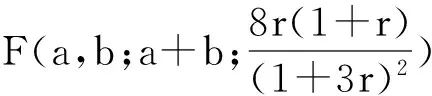
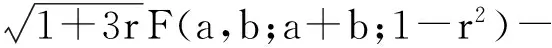

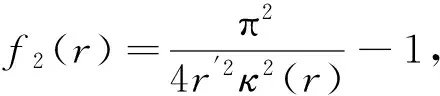
3 定理的证明
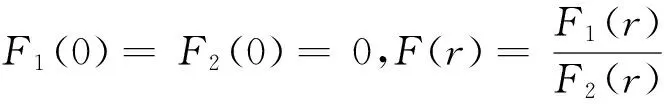
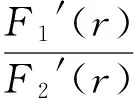
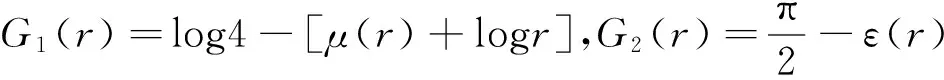
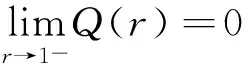
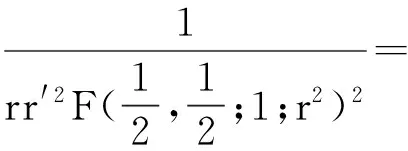
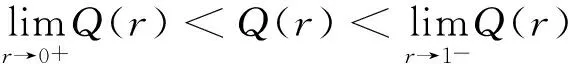

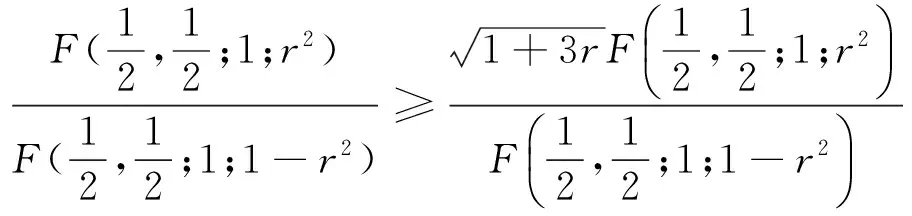
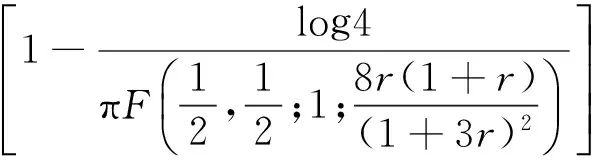
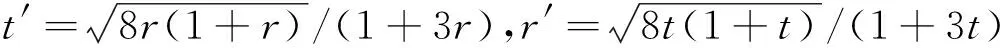

4 结 论
