2-UPR-RPU并联机构的静力学分析

王中林，张宁斌，李秦川，陈巧红

(浙江理工大学，a.机械与自动控制学院；b.信息学院，杭州 310018)



2-UPR-RPU并联机构的静力学分析

王中林a，张宁斌a，李秦川a，陈巧红b

(浙江理工大学，a.机械与自动控制学院；b.信息学院，杭州 310018)

2-UPR-RPU并联机构可以实现2个转动自由度及1个移动自由度，文章对该机构结构进行了静力学分析。通过构件矢量法分别对2-UPR-RPU并联机构分支杆件及动平台建立静力平衡方程，再由该并联机构杆件小变形原理建立变形协调方程，最后统一到动坐标系中求解该机构在不同运动算例下的驱动力、约束力随时间的变化曲线。结果表明，该机构绕u轴的转动自由度对驱动力的影响较大。研究结果可为2-UPR-RPU并联机构运动学分析、动力学分析及控制过程实现等后续研究提供静力学理论基础。

并联机构；少自由度；静力学分析

0　引　言

少自由度并联机构[1]的自由度少于6，与串联机构相比，少自由度并联机构刚度大、运动精度高、负载能力强；与6自由度并联机构相比，少自由度并联机构结构简单、驱动关节少、易于控制、成本较低，因此少自由度并联机构具有更好的应用前景[2-3]，已成为当下研究的热点。

机构静力学分析在实际的工业应用中非常重要，许多机械设备在实际应用中都需要很强的静承载力，如机床定点工作、天文望远镜等。并联机构静力分析是并联机构设计中重要内容，包括驱动力、运动副上约束力及机构最大载荷等，它是动力学分析、结构设计、强度校核等的基础。

目前并联机构的静力学分析研究已经取得一定的进展，文献中所涉及的机构静力分析方法有螺旋理论法、矢量法、影响系数法等。Hubert等[4]通过对机构静力学分析来判断机构奇异边界。赵燕等[5-6]分析了并联机构运动副上的主动力和约束力情况。李永刚等[7]在微分流形理论的基础上，指出了机械臂末端执行器的广义力空间。高峰等[8]提出了一种新型机器人五维力和力矩传感器，并分析其力学特性，发现它的解耦和各向同性。Lu[9]利用虚功原理求解空间并联机构的驱动力和被动力。周玉林等[10-11]通过拆杆法以及考虑机构微小变形建立并联机构的静力学模型，分析各运动副上受力情况。李永泉等[12]通过建立大量的变形协调方程对二自由度冗余驱动并联机构进行静力全解。艾青林等[13]论述了以刚性杆、柔性杆连接并联机构动定平台时机构的静力特性。

本文采用矢量法建立机构的静力学平衡方程，并利用构件小变形叠加原理建立变形协调补充方程，对3自由度并联机构2-UPR-RPU进行静力学分析，求得该机构的驱动力及运动副约束反力随时间的变化曲线，以期为该机构的运动学分析、动力学分析及控制过程实现等后续研究提供静力学理论基础。

1　2-UPR-RPU并联机构简介

2-UPR-RPU并联机构包含定平台、动平台以及3个分支，其示意图如图1所示。分支1、2为UPR分支，分支3为RPU分支(U表示万向铰，P表示移动副，R表示转动副)。动平台通过B1、B2处的R副以及B3处的U副与3分支连接在一起；定平台通过A1、A2处的U副以及A3处的R副与3分支连接在一起。3个分支的驱动副为P副，即图1中bi(i=1,2,3)。机构中动平台与定平台形状均为等腰直角三角形，即OA1=OA2=OA3=r1、oB1=oB2=oB3=r2。定坐标系原点O位于△A1A2A3斜边中点处，动坐标系原点o位于△B1B2B3斜边中点处。

图1　2-UPR-RPU并联机构示意图

固定坐标系中X轴与OA3重合，Y轴与OA1重合，Z 轴为垂直向下；动坐标系中u 轴与oB3重合，v 轴与oB1重合，w轴方向根据右手螺旋法则确定。对于分支1、2的分支坐标系，xi(i=1,2)轴与B1、B2处的R副轴线重合，方向如图1所示，zi(i=1,2)轴与分支1、2的杆件重合，方向如图1所示，yi(i=1,2)轴的方向根据右手螺旋法则确定。对于分支3的分支坐标系，x3轴与A3处的R副轴线重合，方向如图1所示，z3轴与分支3的杆件重合，方向如图1所示，y3轴方向根据右手螺旋法则确定。B1、B2处的R副轴线平行于u 轴，A3处的R副轴线平行于Y轴。此外，αi(i=1,2)表示zi(i=1,2)与w轴之间的夹角，α3表示z3与Z轴之间的夹角。

根据柴馨雪等[14]对2-UPR-RPU并联机构奇异性分析可知，该并联机构具有2转动1移动3自由度。在图1中，该机构的3个自由度分别为绕Y轴、u轴的转动以及沿移动副方向的移动。

3　2-UPR-RPU并联机构静力分析

作用在动平台上中心点处的力/力矩在动坐标系o-uvw中可表示为6维力/力矩形式：

Fh= (Thx,Thy,Thz,fhx,fhy,fhz)T

(3)

由于6维力/力矩的作用使得各分支杆件的上部(ui)和下部(si)所受到的力/力矩表示为下列形式：

(4)

其中：i表示分支；ui表示分支上部，即Aibi；si表示分支下部，即biBi；j为ui或si。

通过将分支杆件的ui和si受到的力/力矩简化到其质心处，得到：

(5)

其中：jc表示ui或si的质心位置。

由图1得分支坐标系向动坐标系的旋转矩阵，即：

(6a)

(6b)

(6c)

其中：s表示正弦函数sin；c表示余弦函数cos。

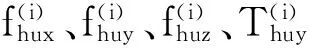
图2　分支静力/力矩示意图

图3　分支下部静力/力矩示意图

图4　动平台静力/力矩示意图

由图2可得AiBi(i=1,2,3)力平衡方程为：

(7)

(8)

A3B3的力矩平衡方程为：

(9)

(10)

si的力矩平衡方程为：

(11)

动平台处的力/力矩平衡方程为：

(12)

(13)

因此可以得到总共45个平衡方程，其中有17个方程中包含主动力及约束反力，写成矩阵形式为：

(14)

4　2-UPR-RPU并联机构数值算例

选取2-UPR-RPU并联机构尺寸参数时，需考虑该机构占地面积、机构平台之间及平台与杆件之间协调性(如定平台尺寸大于动平台尺寸)、实际的装配问题等。在本文算例中，参数值根据经验选取，参数值选取不同其静力学分析结果不同。为使2-UPR-RPU并联机构静力求解过程简单化、求解结果容易验证，文中假设该并联机构动平台只受到沿w轴方向的力，即FN=80N，其中动平台所受的力改变之后，该机构静力学求解结果也将随之变化。综上所述，2-UPR-RPU并联机构相关参数如表1所示。

表1　参数值

因为并联机构具有3个自由度，本文用z表示在Z轴上的移动，α表示绕u轴转动，β表示绕Y轴转动。在初始位型处，并联机构动平台与定平台处于平行位置，动平台中心点o处受到轴向力FN，沿w轴方向。由于机构低速运转，所以不考虑机构内部作用力，可得：

(15)

4.1算例1

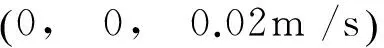
图　5　算例1示意图

如图5所示，在初始位型下该并联机构只作垂直向下运动，所以该机构各分支杆长长度一致，即：

(16)

及

(17)

图6　驱动力及约束反力

4.2算例2

机构处于初始位型，z=z0、β=0、α=30°，改变α的值，其中的变化范围为非全局的。算例2示意图如图7所示，令vz=0、ωα=6°/s、t= 10s 。

图7　算例2示意图

图8　驱动力与约束反力

4.3算例3

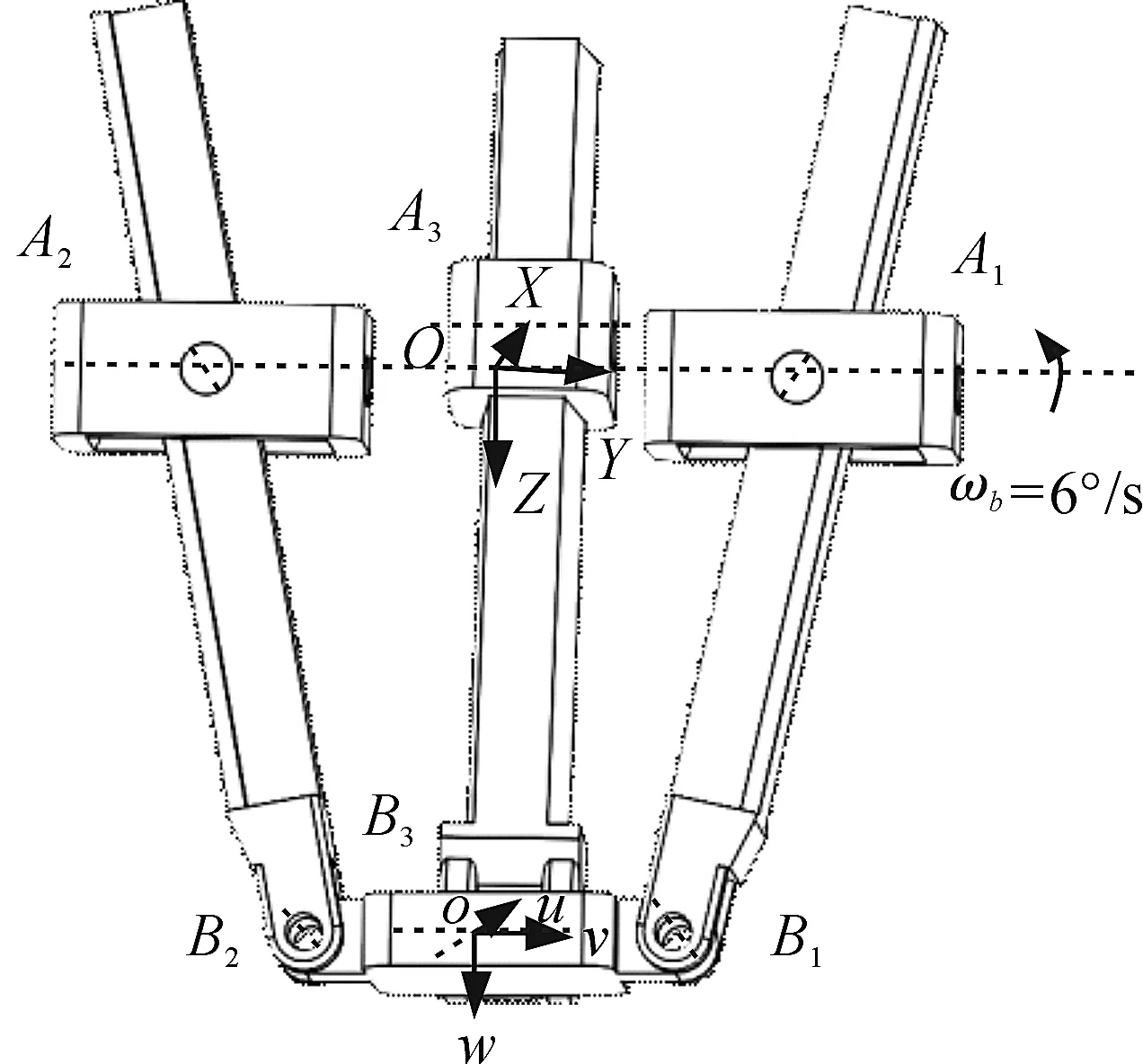
图9　算例3示意图

图10　驱动力与约束反力

4.4算例4

图11　驱动力示意图

5　结　论

a)绕u轴的转角α角对2-UPR-RPU并联机构驱动力的影响比绕Y轴的转角β、沿P副移动量z对其驱动力的影响更大；

b)在设计2-UPR-RPU并联机构时需要考虑该机构驱动力较大的情形，由于该并联机构运动副

中的约束反力可能会出现较大变化，因此该机构的强度校核显得尤为重要;

[1] 黄真,赵永生,赵铁石.高等空间机构学[M].高等教育出版社,2006:127-138.

[2] 黄真,李秦川.少自由度并联机器人机构的型综合原理[J].中国科学E辑:技术科学,2003,33(9):813-819.

[3] 路懿,胡波.少自由度并联机构研究进展[J].燕山大学学报,2011,35(5):377-384.

[4]HUBERTJ,MERLETJP.Staticofparallelmanipulatorsandclosenesstosingularity[J].JournalofMechanismsandRobotics, 2009, 1(1): 1-6.

[5] 赵燕,黄真.3-RPS并联机构的主动力和约束力分析[J].燕山大学学报,2008,32(4):299-303.

[6] 赵燕,黄真.含过约束力偶的少自由度并联机构的受力分析[J].机械工程学报,2010,46(5):15-21.

[7] 李永刚,宋轶民,黄田,等.少自由度并联机器人机构的静力分析[J].机械工程学报,2007,43(9):80-83.

[8] 高峰,陈玉龙,彭斌彬,等.新型解耦和各向同性五维力传感器性能分析[J].机械工程学报,2004,40(9):71-74.

[9]LUY.UsingvirtualworktheoryandCADfunctionalitiesforsolvingactiveforceandpassiveforceofspatialparallelmanipulators[J].MechanismandMachineTheory, 2007, 42(7): 839-858.

[10] 周玉林,刘磊,高峰.3自由度球面并联机构3-RRR静力全解[J].机械工程学报,2008,44(6):169-176.

[11] 周玉林,李波,杨龙,等.二自由度球面并联机构UP+R静力学分析[J].中国机械工程,2013,24(15):2081-2087.

[12] 李永泉,张立杰,郭菲,等.球面2-DOF冗余驱动并联机器人静力学全解[J].机械工程学报,2011,47(19):22-29.

[13] 艾青林,黄伟锋,张洪涛,等.并联机器人刚度与静力学研究现状与进展[J].力学进展,2012,42(5):583-592.

[14] 柴馨雪,项济南,李秦川.2-UPR-RPU并联机构奇异分析[J].机械工程学报,2015，51(13):144-152.

(责任编辑： 康锋)

Static Analysis of 2-UPR-RPU Parallel Manipulator

WANGZhonglina，ZHANGNingbina，LIQinchuana，CHENQiaohongb

(a. Faculty of Mechanical Engineering & Automation；b. School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)

2-UPR-RPU parallel manipulator has two rotational degrees of freedom and one translational degree of freedom. A static analysis is provided for the structure of mechanism. An equation of static equilibrium was built for the branch rod piece of 2-UPR-RPU parallel mechanism and mobile platform by means of component vector method. Then, a compatibility equation of deformation was established according to the principle of small deformation of such parallel mechanism rod piece. In the end, the change curve of driving force and the binding force of 2-UPR-RPU with time history in a unified moving coordinate system were calculated. The results of this paper show that the driving force of 2-UPR-RPU is greatly affected by the rotational degrees of freedom of the u axis. The research results can provide static theoretical bases for the following researches, such as kinematic analysis, dynamic analysis and control process realization of 2-UPR-RPU parallel mechanism.

parallel mechanism；lower-mobility；static analysis

10.3969/j.issn.1673-3851.2016.05.009

2015-08-30

国家自然科学基金项目(51275479)

王中林 (1989-)，男，江苏连云港人，硕士研究生，研究方向为并联机器人。

陈巧红，E-mail：chen_lisa@zstu.edu.cn

TP24

A

1673- 3851 (2016) 03- 0372- 07 引用页码： 050401