基于地震属性建模的数值模拟及其应用

李良泉, 熊晓军, 侯秋平, 杨瑞齐, 陈　琴

(1.地球探测与信息技术教育部重点实验室(成都理工大学),成都 610059;2.中国石油川庆钻探工程有限公司 地质勘探开发研究院，成都 610051)



基于地震属性建模的数值模拟及其应用

李良泉1, 熊晓军1, 侯秋平1, 杨瑞齐1, 陈琴2

(1.地球探测与信息技术教育部重点实验室(成都理工大学),成都 610059;2.中国石油川庆钻探工程有限公司 地质勘探开发研究院，成都 610051)

为了解决花岗岩潜山储层内部结构复杂、非均质性强、在数值模拟建模过程中模型参数填充误差大的问题，本文提出了一种基于地震属性建模的数值模拟技术。该技术首先优选地震属性建立储层模型；然后采用波动方程的数值模拟方法对模型进行“正演+偏移”计算，并对比分析模拟得到的偏移剖面与原始地震剖面，逐步修正观测系统参数，直至两者的主要特征一致；最后，结合其他地震属性(如裂缝检测属性)，综合分析目的层的地震响应特征。对渤海某区花岗岩储层的数值模拟结果表明，该方法有效地刻画了花岗岩“溶蚀孔隙+高角度裂缝”所形成的“串珠状”反射特征，为该区后续的勘探研究奠定了基础。利用本文提出的方法综合分析储层结构的地震波场特征是一种可行的方法，该方法除了应用于花岗岩储层的数值模拟外，还可以应用于其他复杂储层的数值模拟。

数值模拟；地震属性；花岗岩；储层模型

随着勘探的不断深入，勘探目标逐渐扩大到非沉积岩储层，其中基岩油气藏正是一个潜在勘探目标。目前世界范围内的基岩潜山油气田中，约40%产于花岗岩潜山储层。中国发现的花岗岩储层油气田大都属于多期变质的混合花岗岩，岩性复杂，地质年代不太准确[1]，对该类储层的评价存在较大困难，属于一个比较难的勘探领域。

本文的研究区是渤海某区的花岗岩储层，目前已有很多学者对该区的花岗岩储层做了大量的基础研究：王昕等[2]对渤海海域PL花岗岩潜山储层的发育机制和储层特征进行了仔细研究，并将潜山内部细分为土壤带、砂-砾质分化带、裂缝带和基质带；王霄[3]对潜山的构造演化、花岗岩储层特征、油源对比及成藏条件进行了剖析，分析潜山内部4个带的储层特性，建立了油气成藏模式；陈国成等[4]综合岩矿和测井资料，分析了花岗岩储层的岩性特征、储集空间类型及物性特征；等。

数值模拟作为勘探开发中一个必不可少的环节，尤其对于花岗岩这种复杂储层，更加显得重要。张华等[5]针对花岗岩裂隙储层各向异性进行了高阶有限差分数值模拟，并认为在实际勘探中可以将花岗岩裂隙介质等效为各向同性介质；黄继新等[6]探讨了一种综合运用地震、测井、地质资料的方法，以大港油田某区块为例建立了基于地质统计和地震反演的定量储层地质模型；龚再升[1]阐述了花岗岩储层油气藏的特点以及花岗岩储层的岩性与分类，总结了花岗岩潜山地震响应特征；等。

考虑到渤海某区花岗岩潜山储层结构复杂，内部物性不均匀，储集空间类型多为孔隙-裂缝型，储层在纵横向均具有较强的非均质性[7]，测井参数统计时精确度不够，且井间信息不足等因素，采用常规的储层建模方法难以准确地反映花岗岩储层的地质特征。因此，本文提出了一种基于地震属性建模的数值模拟技术，利用该技术得到研究区的数值模拟剖面，并总结花岗岩储层的地震反射特征。

1　方法原理

本文提出的基于地震属性建模的数值模拟技术，首先建立基于地震属性的储层模型；然后对储层模型采用波动方程方法进行数值模拟，得到模拟结果；最后综合其他地震属性进行分析。图1为基于地震属性建模的数值模拟技术流程图。

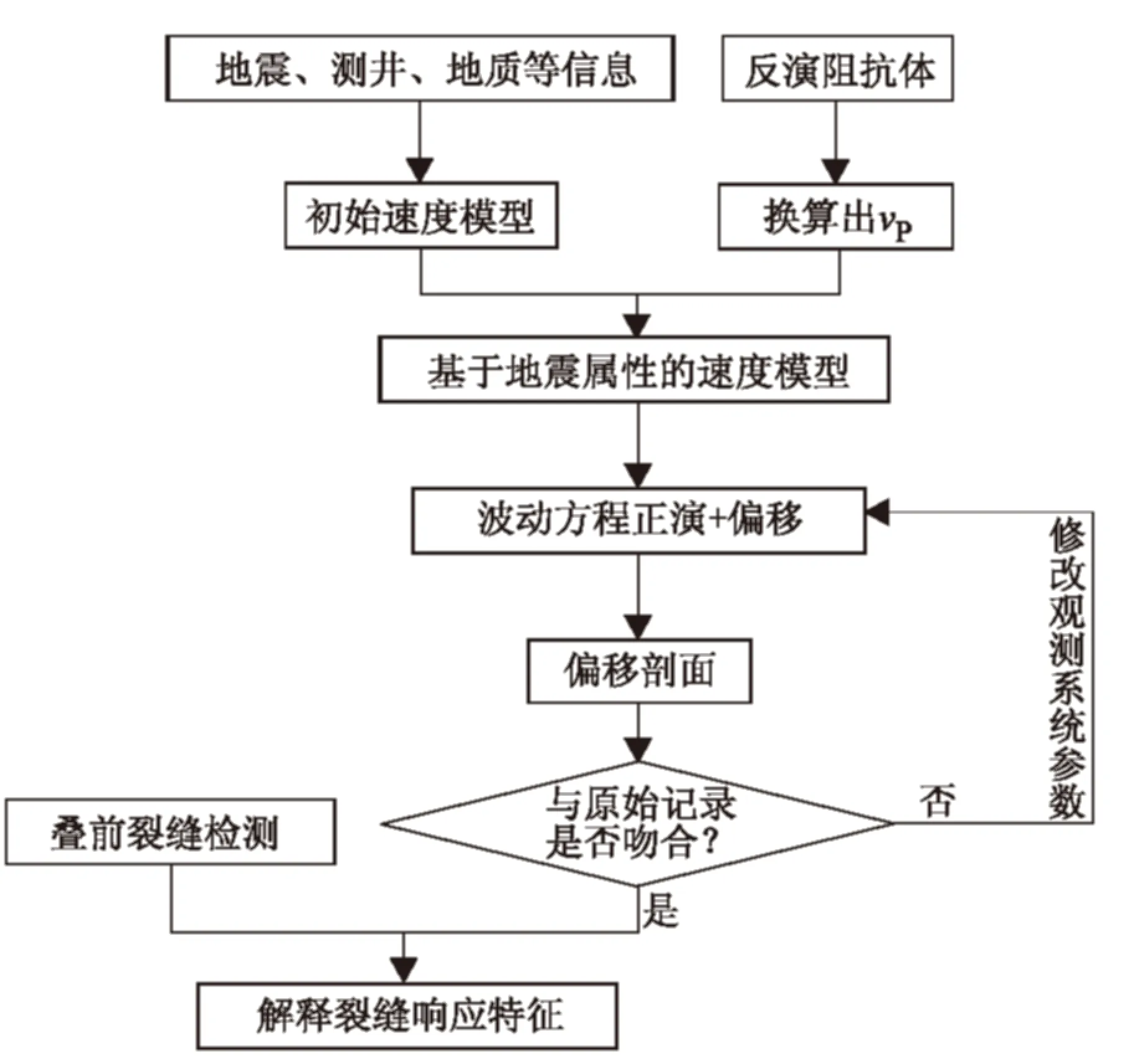
图1　技术流程图Fig.1　Technique flow chart for seismic attribution

1.1基于地震属性的储层建模

对于数值模拟，储层模型的建立至关重要，也是制约数值模拟结果的重要因素；此外，模型的精度也直接影响数值模拟的准确性。基于地震属性的建模技术包含下述3个步骤。

a.首先优选过井剖面，综合利用目的层位、断层发育，以及地质纵向分带等信息建立初始模型框架；然后整理和统计测井数据，对模型框架进行物性参数填充，从而建立参数模型。

b.利用叠前EI反演的纵波阻抗数据换算出纵波速度。

常用的密度、速度、波阻抗之间转换的经验公式有Gardner公式[8]、Lindseth公式[9]等，本文根据Gardner经验公式形式，利用最小二乘法进行系数拟合，得到波阻抗(Z)与速度(v)之间的换算关系式。Gardner经验公式如下[8]

ρ=a vm

(1)

对(1)式两边取对数可得

lnρ=mlnv+lna

(2)

根据测井曲线处密度(ρ)和速度(v)的值，采用最小二乘法对(2)式的系数a和m进行拟合。

通过对研究区的花岗岩储层的测井曲线统计分析，可得公式(2)中的系数为a=1.175 7，m=0.089 8。由此可得波阻(Z)抗与速度的转换公式

v=0.859Z0.917

(3)

c.根据层位控制，利用换算出的纵波速度对初始模型进行速度替换，建立最终模型。

1.2数值模拟方法原理

波动方程数值模拟可以分为单程波动方程数值模拟和双程波动方程数值模拟。为了模拟花岗岩储层的主要反射特征，正确模拟它的一次反射波已满足需要，因此本文采用单程波动方程数值模拟方法[10]。

对于各向同性介质，取二维标量声波方程作为延拓的基本方程

(4)

式中:P=P(x,z,t)为二维地震波场；t为时间；v(x,z)为纵、横向都可变的地震波传播速度。

对于波动方程数值模拟而言，波场延拓至关重要。目前常用的频率-波数域波场延拓方法有相移法(PS)[11]、相位移加插值方法(PSPI)[12]、裂步傅里叶方法(SSF)[13]、傅里叶有限差分方法(FFD)[14]、广义屏方法(GSP)等。综合考虑地震波场数值模拟的精度和计算效率等因素，本文选择裂步傅里叶方法进行频率-波数域的波场延拓计算。

首先定义速度的倒数为慢度，设地下介质每一点的慢度为s(x,z)，将慢度分解为横向可变和横向不变两部分[10]

s(x,z)=s0(z)+Δs(x,z)

(5)

将式(5)代入式(4)，并将波动方程变换到频率域，得

(6)

略去Δs2得

(7)

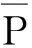
(8)

使用参考慢度s0(z)作相移延拓

(9)

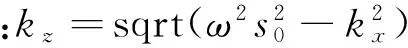
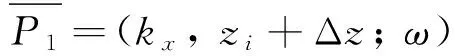
P1(x, zi+Δz; ω)=

(10)

在频率-空间域中，对慢度的扰动Δs(x,z)，使用第二次相移延拓

P1(x, zi+Δz; ω)·eiωΔs(x, zi)

(11)

在t=0时成像

(12)

式(9)、(11)构成分步傅里叶波场延拓的基本公式，式(9)在频率-波数域实现，式(11)在频率-空间域实现。

2　实例分析

本文研究区的花岗岩储层为中生界花岗岩，主要受表生喀斯特作用、有机酸溶蚀作用、构造变形作用及微古地貌作用的共同控制，由表及里随着风化淋滤作用的逐渐减弱，可以划分为土壤带、砂-砾质风化带、裂缝带和基岩带，储集空间由孔隙型→裂缝-孔隙型→孔隙-裂缝型→裂缝型呈现规律性的变化[2]。

2.1实际剖面与典型属性分析

图2是研究区原始地震资料，t8层位为潜山顶界面，向下依次是潜山顶往下30 ms, 60 ms, 150 ms层位。t8层(潜山顶界面)位于波峰，呈连续的强振幅反射特征，该波峰下波谷能量在横向上不连续；潜山内部没有出现连续反射波组，可见弱振幅、非连续或块状、空白状杂乱反射特征。

笔者对地震属性进行了优选，考虑到阻抗数据最能精细体现研究区纵横向的地质特征，且与速度关系密切，故选波阻抗作为建模过程中的约束条件。图3是叠前反演的纵波阻抗剖面，红色部分是波阻抗相对较低的区域，大多分布在潜山顶界向下60 ms范围内。

渤海A井完钻深度为潜山顶界面向下255 m，钻遇储层厚度为125.4 m。其中, t8-(t8+30 ms)内储层厚度为37.8 m，t8-(t8+60 ms)内储层厚度为85.7 m。图4是叠前裂缝检测剖面，红色代表裂缝发育体。根据测井数据统计：“土壤

图4　叠前裂缝检测剖面Fig.4　Fracture detection in pre-stack section

带+风化带”主要分布在t8-(t8+30 ms)范围内，以孔隙发育为主，裂缝欠发育；“裂缝带”主要分布在(t8+30 ms)-(t8+60 ms)范围内，大量发育高角度裂缝。图中叠前裂缝检测结果与测井信息相符。

2.2储层数值模拟

2.2.1储层建模

根据本文提出的基于地震属性的建模方法建立渤海某工区的最终地质模型(图5)。

由于风化带和裂缝带内孔隙、裂缝的存在，导致t8-(t8+60 ms)范围内低速体大量发育。图5中红色代表低速体，可见低速体多发育在t8-(t8+60 ms)之间，与测井信息相符。该速度模型的准确性为接下来的数值模拟提供了保障。

2.2.2数值模拟与分析

对建立的最终模型采用波动方程数值模拟，得到偏移剖面(图6)。

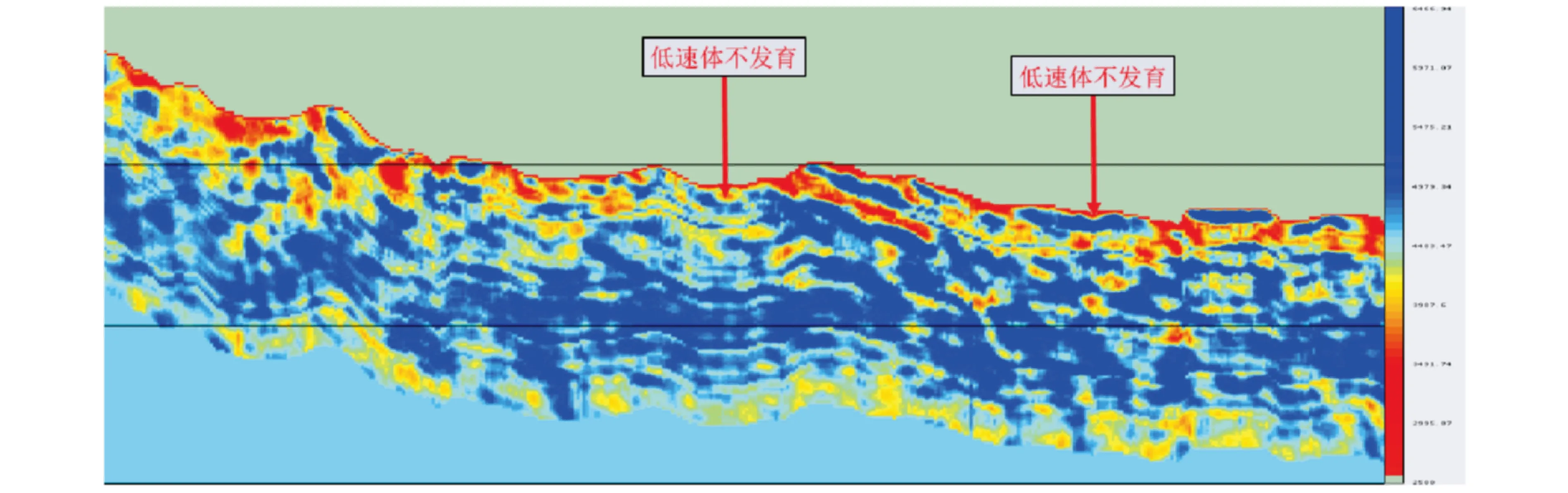
图5　速度模型Fig.5　Velocity model

图6　基于图5的数值模拟偏移剖面Fig.6　Numerical simulation of shifting section based on Fig.5

由图6可以看出，t8位于一个连续强波峰，其下方的波谷能量横向上变换较大，潜山顶界(t8)以下波形杂乱，与实际剖面特征一致；数值模拟剖面中出现“串珠状”特征，与典型的“串珠状”特征(短段的波峰波谷交替出现)相符合(图7)。

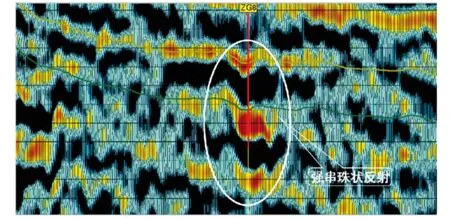
图7　塔中地区中古8井区典型“串珠状”地震反射特征Fig.7　Typical paternoster reflection characteristics in Tazhong area资料来源：塔中地区中古8井区

此外，综合地震属性剖面(图3、图4和图5)和数值模拟剖面(图6)可见：(1)通过速度模型(图5)和偏移剖面(图6)的对比分析可以看出：风化带内低速体不发育的区域对应较连续的波谷(t8波峰下的第1个波谷)特征；低速体发育区域对应的波能量呈中弱反射特征，并且横向连续性变差。(2)通过叠前裂缝检测剖面(图4)和偏移剖面(图6)的对比分析可以看出：裂缝大量发育区，正演记录上出现“串珠状”特征，波峰与波谷交替出现；随着裂缝纵向展布增大，波峰和波谷能量均增强(串珠3与串珠4对应的位置)。

3　结 论

a.对于花岗岩潜山储层，由于其内部结构复杂、非均质性强、内部物性不均匀，常规建模技术难以满足要求；利用本文提出的属性建模方法，有效避免了参数填充不准确的问题，提高了模型的纵横向精度。

b.基于波动方程数值模拟得到的偏移剖面能很好地反映潜山内部储层结构的主要波场特征。模拟结果表明渤海某区花岗岩潜山顶界面呈强反射特征，潜山内部由于物性不均匀导致反射特征杂乱。

c.通过模拟结果与叠前裂缝检测剖面的对比分析，总结了渤海某区花岗岩潜山储层“溶蚀孔隙+高角度裂缝”形成的“串珠状”地震响应特征，为后续储层预测奠定了基础。

d.本文研究表明，结合地震属性与数值模拟结果，综合分析储层结构的地震波场特征是一种可行的方法。该方法除了应用于花岗岩储层的数值模拟外，还可以应用于其他复杂储层的数值模拟，具有较强的实际应用价值。

[1] 龚再升.继续勘探中国近海盆地花岗岩储层油气藏[J].中国海上油气,2010,22(4):213-220.

Gong Z S. Continued exploration of granitic-reservoir hydrocarbon accumulations in China offshore basins [J]. China Offshore Oil and Gas, 2010, 22(4): 213-220. (In Chinese)

[2] 王昕,周心怀,徐国胜,等.渤海海域蓬莱9-1花岗岩潜山大型油气田储层发育特征与主控因素[J].石油与天然气地质,2015,36(2):262-270.

Wang X, Zhou X H, Xu G S,etal. Characteristics and controlling factors of reservoirs in Penglai 9-1 large-scale oilfield in buried granite hills, Bohai Sea [J]. Oil & Gas Geology, 2015, 36(2): 262-270. (In Chinese)

[3] 王霄.蓬莱9-1构造花岗岩古潜山油气成藏条件与成藏模式[D].成都:成都理工大学档案馆,2015.

Wang X. The Hydrocarbon Accumulation Conditions and Accumulation Mode of Granite Buried Hill in Penglai 9-1 Structure [D]. Chengdu: The Archive of Chengdu University of Technology, 2015. (In Chinese)

[4] 陈国成,陈华靖,田晓平.渤海PL油田花岗岩潜山储层发育特征及控制因素[J].海洋地质前沿, 2016,32(2):14-19.

Chen G C, Chen H J, Tian X P. Characteristics and controlling factors of granitic buried-hill reservoir in PL oilfield of Bohai Sea [J]. Frontiers of Marine Geology, 2016, 32(2): 14-19. (In Chinese)

[5] 张华,龚育龄.花岗岩裂隙储层各向异性高阶有限差分数值模拟[J].东华理工大学学报(自然科学版),2012, 35(4):416-421.

Zhang H, Gong Y L. Anisotropic numerical simulation of fracture reservoir in granite with high-order finite difference[J]. Journal of East China Institute of Technology (Natural Science Edition), 2012, 35(4): 416-421. (In Chinese)

[6] 黄继新,彭仕宓,黄述旺.河流相储层建模中测井和地震资料整合研究[J].中国矿业大学学报,2007,36(1):126-131.

Huang J X, Peng S M, Huang S W, Study of integrating seismic and logging data in fluvial reservoir modeling[J]. Journal of China University of Mining & Technology, 2007, 36(1): 126-131. (In Chinese)

[7] 谭伟雄,王俊瑞,邓强,等.花岗岩储层储集性能定量评价方法及应用[J].中国海上油气,2015,27(2):31-38.

Tan W X, Wang J R, Deng Q,etal. Quantitative evaluation method for granite reservoir properties and its applications[J]. China Offshore Oil and Gas, 2015, 27(2): 31-38. (In Chinese)

[8] Gardner G H F, Gardner L W, Gregory A R. Formation velocity and density-the diagnostic basics for stratigraphic traps[J]. Geophysics, 2012, 39(6): 770.

[9] Lindseth R O. Synthetic sonic logs — a process for stratigraphic interpretation[J]. Journal of Virology, 1994, 68(11): 7559-7565.

[10] 熊晓军.单程波动方程地震数值模拟新方法研究[D]. 成都:成都理工大学档案馆, 2007.

Xiong X J. Method Research of One-Way Wave-Equation Seismic Numerical Simulation [D]. Chengdu: The Archive of Chengdu University of technology, 2007. (In Chinese)

[11] Gazdag J. Wave equation migration with the phase-shift method[J]. Geophysics, 2012, 43(7): 1342-1351.

[12] Gazdag J. Migration of seismic data by phase shift plus interpolation[J]. Geophysics, 1984, 49(2):124-131.

[13] Stoffa P L, Fokkema J T, Freire R M D L,etal. Split-step Fourier migration[J]. Geophysics, 1990, 55(4): 410-421.

[14] Ristow D, Rühl T. Fourier finite-difference migration[J]. Geophysics, 1994, 59(12): 1882-1893.

Numerical simulation and its application based on modeling of seismic attribution

LI Liang-quan1, XIONG Xiao-jun1, HOU Qiu-ping1, YANG Rui-qi1, CHEN Qin2

1.KeyLaboratoryofEarthExploration&InformationTechniquesofChinaMinistryofEducation,ChengduUniversityofTechnology,Chengdu610059,China;2.GeophysicalProspectingCompany,ChuanqingDrillingEngineeringCompany,CNPC,Chengdu610051,China

A numerical simulation method based on modeling constrained by seismic attribution is proposed to cope with the complex structure, strong heterogeneity and inhomogeneity in exploration of granite buried hill reservoirs. Firstly, reservoir model is established by selecting preferred seismic attribution followed by simulation by wave equation to get a satisfied result; then, the simulated cross section and original cross section are correlated and the observation parameters are revised until the major characteristics of the two cross sections reach unanimous. The numerical simulation on granite reservoir in Bohai area indicates that this method can efficiently describe “the string of beads-like” reflection characteristics caused by high angle fractures and corroded fissures in granite, which is very important to subsequent exploration of oil and gas. The numerical simulation method can apply to granite reservoirs and other complex reservoirs.

numerical simulation; seismic attribution; granite; reservoir model

10.3969/j.issn.1671-9727.2016.04.09

1671-9727(2016)04-0454-06

2016-04-30。

国家自然科学基金项目(41274130)。

李良泉(1993-),男,硕士研究生,研究方向:复杂储层地震波场数值模拟, E-mail:452484842@qq.com。

P631.4

A