随机需求下横向并购供应链网络整合优化策略研究

康　凯　卢山山　张庆红

1(河北工业大学，天津　300401)　2(石家庄铁道大学，石家庄　050043)

随机需求下横向并购供应链网络整合优化策略研究

康凯1卢山山1张庆红2

1(河北工业大学，天津300401)2(石家庄铁道大学，石家庄050043)

〔摘要〕本文从系统优化视角，针对增设集散中心的横向并购供应链网络整合策略，利用变分不等式建立了随机需求下的整合优化模型。以市场链为主线，以供应链网络均衡理论为基础，构建了以横向并购供应链网络活动总成本最小为目标的数学模型，通过转换成变分不等式采用改进的欧拉算法进行模型求解。通过数值算例进一步说明了模型的适用性和灵活性，得出了增设集散中心的并购整合策略能够降低供应链网络的平均运营成本的结论，通过对比不同市场紧密程度下产生的供应链网络平均成本协同效应，发现随着市场紧密程度的增加其协同效应更明显，为横向并购供应链网络整合优化提供理论依据与方法。

〔关键词〕横向并购供应链网络集散中心随机需求变分不等式

引言

随着全球化竞争趋势的加剧，并购已成为企业适应复杂多变的市场环境并实现快速成长的重要途径。企业间的竞争已转化为供应链间的竞争[1]，现在供应链的有效整合已成为企业并购成功的重要标志之一[2]。并购之后供应链整合优化策略依然是并购整合的重要实践课题。

企业并购的供应链网络整合本质是供应链网络结构的再设计。Anna Nagurney利用变分不等式方法研究了横向并购的供应链网络整合问题，探究了横向并购供应链网络整合产生的成本协同问题[3]，并基于该思路，研究了多产品情形[4]和多目标情形下供应链网络整合的协同效应(成本协同和环境协同)[5]。Anna Nagurney一系列的研究成果为横向并购供应链网络整合奠定了理论基础，其研究成果仅考虑了需求确定和集中决策条件下供应链整合优化问题，未涉及需求随机情形和供应链节点企业利益均衡问题。姚锋敏和滕春贤等人基于Anna Nagurney研究思路探究了需求随机情形下供应链网络均衡问题[6]，利用二层规划方法探讨了利益协调问题[7]。黄青紫利用混合整数规划模型研究了核心企业发生横向并购后供应商和分销商的整合问题[8]；曾敏刚探究了数量折扣、规模效应和学习曲线对横向并购整合前后利润产生的影响及分销商和零售商的选择问题[9]；陈静基于二级供应链网络构建了差异化产品供应链横向并购模型，对比了不同决策机制下横向并购模式产生的效应[10]。蒋铁生和彭永涛利用变分不等式分别研究了需求随机情况下的供应链网络节点能力和流量设计问题[11]以及具有随机供需特征的物流超网络优化设计问题[12]。

上述研究探究了供应链网络阶层不变策略下的供应链网络整合优化再设计问题。基于现实考虑横向并购供应链网络整合问题，增设供应集散中心和分销集散中心作为横向并购后供应链网络整合的重要方式，可以达到节约成本、改变服务、增加灵活性的目的，使核心企业专注于核心业务[13]。于此，本文试图研究供应链网络阶层增加策略的横向并购供应链网络优化模型，为横向并购供应链网络整合优化提供理论依据与方法。

1　问题描述和假设

1.1问题描述

本文以横向并购供应链网络阶层增加策略下的供应链网络整合优化为研究对象，并购企业A和被并购企业B在横向并购之前，各自拥有以制造活动为起点、经过分销中心、以零售活动为终点的供应链网络，生产同质产品，面对随机需求市场。

图1　横向并购前A、B两企业的供应链网络拓扑结构图

并购之前A、B两企业的供应链网络拓扑结构图如图1所示，其中网络图中的节点表示企业，边表示节点企业的经济活动，如制造、运输、存储和分销等活动，每条边上的流量表示节点企业的经济活动所涉及到的产品数量。A、B两企业并购后，采取供应链网络融合策略，即两企业的制造中心和分销中心在网络优化过程中具有同等地位，同时在制造中心和分销中心间建立分销集散中心，并在制造中心和集散中心之间、集散中心和分销中心之间、分销中心和零售商之间新增交叉运输路径，其并购后的供应链网络拓扑结构图如图2所示。

图2　横向并购后并购企业的供应链网络拓扑结构图

基于图2所示的供应链网络拓扑结构图，本文将供应链网络活动划分为以制造中心、集散中心、分销中心为核心的两阶段三层级活动，并定义了每个层级活动的成本构成。本文从系统优化视角，构建以网络产品流量、产品销售价格为决策变量，在随机需求情景下整个供应链网络活动总成本最小化为目标函数的数学模型，通过构建变分不等式求解最优平衡状态下的产品流量和产品销售价格，并对流量为零的边和节点予以剔除，最终实现对供应链网络结构的整合优化。

对横向并购供应链网络两阶段三层级网络成本的定义为：第一层网络活动为制造中心的制造活动及与集散中心的交易活动，相应成本包括：生产成本，交易成本；第二层网络活动为集散中心的外包或者建设活动及与分销中心的交易活动，相应成本包括：外包成本，交易成本；第三层网络活动为分销中心的存储活动及与零售商的交易活动，相应成本包括：存储成本，交易成本。通过运用市场链的概念可以将上述三层级成本统一表示，同时将零售商的产品处理成本和由于随机需求产生的惩罚成本纳入到供应链网络成本中。

1.2符号变量

fa表示边a上的产品流量，∀a∈L；

xp表示市场链p上的产品流量，∀p∈Pwk∈P；

sk表示供应链网络提供给零售商k的产品供应量，k=1，…，K；

dk表示零售商k的市场需求量，k=1，…，K；

ca(fa)表示边a的活动成本函数，∀a∈L；

ρk表示零售商k的产品销售价格，k=1，…，K；

ρ表示包含各零售商产品销售价格的集合向量，即ρ=[ρ1，…，ρk，…，ρK]，k=1，…，K；

1.3假设条件

(1)假设并购前后两企业生产同一种产品；

(2)分销集散中心的设立采取外包给3PL、4PL的形式产生外包成本，采取核心企业自建形式会产生建设成本、产品的存储成本和集散成本，本文为统一均定义为外包成本；

(3)仅考虑分销中心有库存，其他节点的库存不予以考虑，产品直接向下游移动；

(4)假设各市场需求随机，其参数设定为各需求市场的产品销售价格集合ρ；

(5)假设各成本函数均为连续可微的凸函数。

2　模型构建

2.1建模分析

由市场链的概念，供应链网络中边流量与市场链流量之间存在一一对应的关系，当δap=1表示市场链p包含边a，否则δap=0，具体表示如下：

fa=∑p∈Pxpδap，?其中，?δap={0，1}，?∀a∈L

(1)

每个零售商k对需求市场的总供应量等于汇集到该零售商的所有市场链流量之和，可表示为：

sk=∑p∈Pwkxp，?k=1，…，K

(2)

根据供应链网络两阶段三层次成本定义，用ca表示供应链网络边上的活动总成本函数，其变量为流经边的产品流量fa，从系统优化的角度出发，根据Wordrop在交通网络中对成本的定义，其边的总成本函数应表示为：

(3)

(4)

在供应链网络中，与需求市场的实际交易量不应该超过供应量和需求量的最小值，即不超过min{sk，dk}。对应的供大于求和供小于求产品流量的期望值设为：

(5)

(6)

(7)

所以在需求随机情形下以整个供应链网络的总成本最小为目标，具体目标函数表示如下：

(8)

St．xp≥0

(9)

在供应链网络优化设计过程中，根据空间价格均衡理论，企业为实现总成本最小或者收益最大，一般而言要使供应链网络活动的边际成本要等于产品定价，各需求市场的市场链流量集合应等于该市场需求，即在集中决策下供应链网络均衡应满足以下条件：

(10)

(11)

在各个零售商的需求市场空间中，当各需求市场的市场链集合均达到均衡状态时，即在满足总成本最小目标的条件下其各市场链的最优流量和最优价格应该满足(10)式和(11)式，也就是在整个供应链网络最优状态下市场链的边际成本一定等于需求市场中的顾客愿意支付的产品价格，市场链的产品供应总量一定等于其需求量。

2.2总优化模型及均衡条件的变分不等式表示

(12)

将(1)～(8)式带入(12)式可得：

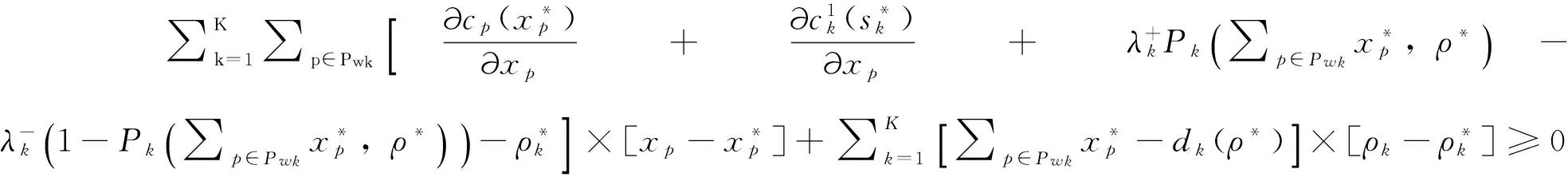
(13)

证明(13)式最优解的存在性和唯一性见文献[16]，这里不予以赘述。

2.3随机需求下横向并购供应链网络平均成本协同表示

为验证供应链网络整合的有效性和必要性，对横向并购整合前后的供应链网络进行成本协同评价，由于探究随机需求视角下的供应链网络整合效果评价，本文以平均成本协同(θ)作为衡量标准对比并购整合前后单位产品的平均成本，其表示形式如下：

(14)

3　求解算法

为解决变分不等式(13)的均衡解问题，本文采用欧拉算法求解，其数学表达式为：

Xτ+1=Pκ(Xτ-ατF(Xτ))

(15)

为提高计算精度，本文采用改进的欧拉算法解决变分不等式(13)的均衡解问题，如下：

Xτ+1=Pκ(Xτ-ατF(Xτ+1))

(16)

具体步骤如下：

3.1初始化

3.2计算

3.3改进

3.4收敛性判断

4　算　例

4.1横向并购前供应链网络的均衡优化解

为了便于计算和分析，假定在并购之前的A、B两企业分别包含2个制造中心，1个分销中心，同时面对2个零售商，其供应链网络结构如图3所示。

在供应链网络中每条边都具有特定的经济活动含义，其相应经济活动及成本函数如表1所示。假设两个零售商面对市场的产品需求量在研究的特定时间段内均服从均匀分布，则有

d1(ρ)∶U[460-ρ1+0.5ρ2，480-ρ1+0.5ρ2]，

d2(ρ)∶U[460-ρ2+0.5ρ1，480-ρ2+0.5ρ1]

根据上述信息，使用改进的欧拉算法，设其

图3　横向并购前A，B两企业的SCN结构

表1　供应链网络的成本函数及最优决策边流量

表2　供应链网络最优决策市场链流量

4.2采取共享分销渠道，增加集散中心策略的横向并购供应链网络均衡优化解

A、B两企业进行并购后，改造横向并购供应链网络，实行共享分销渠道和增设集散中心整合策略的供应链网络结构如图4所示。新增集散中心会增加制造中心和集散中心的交易活动(如边5、6、7、8、9、10、11、12)，集散中心的建设或外包活动(如边13、14)，集散中心与存储中心的交易活动(如边15、16、17、18)，相应活动成本函数如表3所示。新增集散中心对下游分销中心而言，进行集中订货，基于规模效应，交易成本降低，并及时满足零售商需求，存储成本和交易成本也降低。在本算例中为不失一般性，加入集散中心之后供应链活动成本降低程度随机，其成本函数如表3所示，面对同算例5.1具有同样均匀分布的随机市场需求，同时零售商的处理成本函数和惩罚成本也如上例所示，运用改进欧拉算法对网络结果进行优化求解，其优化结果如表3、表4所示。

图4　采取增设集散中心整合策略SCN结构

边a含 义^Ca(fa)f*a1234生产成本函数0.5f21+f1204.0860.1f22+0.5f2335.631f23+0.25f3146.4802f24+f494.01756789101112交易成本函数0.2f25+0.2f599.4460.04f26+0.02f6104.6400.04f27+0.04f7187.2550.02f28+0.08f8148.3760.1f29+0.04f975.9150.12f210+0.1f1070.5650.01f211+0.04f1148.0090.02f212+0.06f1246.008

续　　表

表4　供应链网络最优决策市场链流量

4.3市场紧密程度对增加集散中心整合策略产生协同效应的影响

为探究在改变影响供应链网均衡的外部条件情况下，加入集散中心对协同效应产生的影响，在本文算例中，假设市场需求不仅受到本市场产品价格的影响，还受到其他市场相关产品价格的影响，假定需求市场的需求量呈均匀分布即

d1(ρ)∶U[460-ρ1+φρ2，480-ρ1+φρ2]，

d2(ρ)∶U[460-ρ2+φρ1，480-ρ2+φρ1]

φ表示其他市场产品价格对该市场需求量的影响程度，本文称之为市场紧密程度，其中0≤φ≤1。影响φ取值大小的相关因素包括市场距离、消费者选择偏好等，φ越接近1表明该市场受其他市场的影响程度越大，即市场越紧密。表5展现不同市场紧密程度下的增设集散中心之后较并购之前供应链网络活动的平均产品销售价格、供给量、平均成本及其协同效应。

表5　在不同市场紧密程度下的并购前后供应链网络平均成本及协同效应

续　　表

为充分说明需求随机情形下采取增设集散中心的并购整合策略，市场紧密程度对横向并购前后产品销售价格、对产品供应量、对供应链网络平均成本、对协同效应产生的影响，通过图6～9可以得到以下结论：

图6　并购前后市场紧密程度对产品销售价格的影响

图7　并购前后市场紧密程度对产品供应量的影响

(1)并购后随着市场紧密程度的增加，产品销售价格有所上升但其数值及上升程度要低于并购前，说明采取增设集散中心供应链网络整合策略有利于产品价格的稳定。

(2)由图7可以看出产品价格下降带来了产品供给量的提升，随着市场紧密程度的增加，并购后的产品供给量的变化范围也低于并购前，便于供应链网络预测产品供给量，降低了由于市场需求随机带来的损失。

图8　并购前后市场紧密程度对供应链网络平均成本的影响

图9　市场紧密程度对并购后供应链网络平均成本协同的影响

(3)随着市场紧密程度的增加，并购前后供应链网络的平均成本均呈上升趋势，但并购后平均成本的数值及其上升程度要远低于并购之前，说明采取增设集散中心的并购整合策略能够有效控制供应链网络成本。

(4)随着市场紧密程度的增加，供应链网络的平均成本协同效应呈上升趋势，说明两个需求市场紧密程度越大，越易产生规模效应，采用增设集散中心的并购整合策略越有效。

5　结　论

本文构建了供应链网络阶层增加策略下的横向并购供应链网络拓扑结构图，建立了随机需求情景下以供应链网络活动总成本最小为目标函数和空间价格均衡理论为优化条件的横向并购供应链网络整合优化模型，运用变分不等式进行模型求解。通过数值算例，比较了横向并购前后供应链网络整合策略的协同效应，表明增设集散中心的并购整合策略是能够产生协同效应的，并发现其效果受到需求市场紧密程度的影响。另外，本文还需要进一步补充完善，在以后的研究中应考虑到随机成本或多产品、多销售渠道等情景因素，对横向并购供应链网络整合策略和优化模型做进一步改进。

参考文献

[1]倪文斌,张怀修.供应链整合研究综述[J].商业经济，2010，(10):68～70

[2]Langabeer,J.,Seifert,D.Supply Chain Integration:The Key to Merger Success(Synergy)[J].Supply Chain Management Review,2003，(7):58～64

[3]Nagurney A.A System-optimization Perspective for Supply Chain Network Integration:The Horizontal Merger Case[J].Transportation Research Part E:Logistics and Transportation Review,2009,45(1):1～15

[4]Nagurney A,Woolley T,Qiang Q.Multiproduct Supply Chain Horizontal Network Integration:Models,Theory,and Computational Results[J].International Transactions in Operational Research,2010,17(3):333～349

[5]Nagurney A,Woolley T.Environmental and Cost Synergy in Supply Chain Network Integration in Mergers and Acquisitions[M].Multiple Criteria Decision Making for Sustainable Energy and Transportation Systems.Springer,2010:57～78

[6]姚锋敏,徐素波,林琳,等.随机需求下的多条竞争供应链的网络均衡模型[J].数学的实践与认识,2015,45(2):97～105

[7]滕春贤,姚锋敏,胡宪武.具有随机需求的多商品流供应链网络均衡模型的研究[J].系统工程理论与实践,2007,14(2):77～83

[8]黄青紫.企业横向并购中供应链的整合[D].南京：南京航空航天大学,2007

[9]曾敏刚,张贵萍,王旭亮,等.企业横向供应链整合的建模与优化[J].华南理工大学学报(社会科学版),2012,14(5):57～63

[10]陈静,计国君.差异化产品供应链横向并购的决策机制与效应分析[J].商业研究,2014,(3):159～168

[11]蒋铁生,李波.基于网络图需求随机的供应链网络设计研究[J].工业工程,2012,15(6):102～107

[12]彭永涛,张锦,王坤.具有随机供需特征的物流超网络优化模型研究[J].交通运输系统工程与信息,2014,14(2):184～191

[13]徐明川.基于4PL的集散中心集中决策供应链库存控制策略研究[J].生产力研究,2008,20:63～65

[14]张瑞昕，王恒山．基于价值增值的复杂供应链网络动态合作联盟研究[J]．工业技术经济，2013，(2)：56～60

[15]Zhang D.A Network Economic Model for Supply Chain Versus Supply Chain Competition[J].Omega:The International Journal of Management Science,2006,34:283～295

[16]June Dong,Ding Zhang.A Supply Chain Network Equilibrium Model With Random Demands[J].European Journal of Operational Research,2004，(156):194～212

(责任编辑：王平)

The Strategy of Supply Chain Network Integration and Optimization in Horizontal Mergers and Acquisitions(M&A)with Stochastic Demand

Kang Kai1Lu Shanshan1Zhang Qinghong2

(1．Hebei University of Technology，Tianjin 300401，China；2．Shijiazhuang Tiedao University，Shijiazhuang 050043，China)

〔Abstract〕From the perspective of system optimization,the paper established the integration and optimization model of supply chain network in horizontal M&A with stochastic demand by using the the variational inequality.And the supply chain network integration strategy of horizontal M&A was constructing distribution centers.Based on the definition of market chain and the theory of supply chain network equiilibrium,the mathematic model was optimized to minimize the total cost of supply chain activities and solved by the improved Euler algorithm.Numerical examples were given to illustrate the applicability and flexibility of the model,and found that the horizontal M&A integration strategies of constructing distributions can reduce the average operating cost of supply chain network.By comparing the average cost synergies under the different market tightness,it found that synergistic effects showed more obvious with market tightness increasing,and provided a theoretical basis and methods for horizontal M&A supply chain network integration and optimization.

〔Key words〕horizontal M&A;supply chain network;distribution center;stochastic demand;variational inequality

〔中图分类号〕F273

〔文献标识码〕A

DOI：10．3969/j．issn．1004-910X．2016．09．006

作者简介：康凯，河北工业大学经济管理学院教授，博士。研究方向：企业网络与协作运营，物流与供应链管理。卢山山，河北工业大学经济管理学院硕士研究生。研究方向：物流与供应链管理，供应链网络优化。张庆红，石家庄铁道大学信息科学与技术学院讲师，博士。研究方向：物流与供应链管理，供应链网络优化。

基金项目：国家社科基金(项目编号：14BGL055)。

收稿日期：2016—05—13