磁悬浮球系统的自适应反演滑模控制

郑建英，于占东

（渤海大学 辽宁 锦州 121013）

磁悬浮球系统的自适应反演滑模控制

郑建英，于占东

（渤海大学 辽宁 锦州 121013）

磁悬浮球系统是一种典型的开环不稳定系统，为了实现磁悬浮球系统的精确控制，而且使系统更具有实际意义，设计了一种自适应反演滑模控制器。在实际控制系统中，不确定性及外加干扰是未知的，本文基于实际应用，利用该系统的线性化模型，来设计此控制器。实验结果表明：所设计的自适应反演滑模控制器与普通滑模控制器相比，能减小系统的抖振，能较好的实现小球的稳定悬浮并具有良好的动态跟踪性能，与自适应滑模控制器相比，能更好的在实践中应用。

磁悬浮球系统；滑模控制器；自适应；反演

磁悬浮系统具有非接触、无摩擦、速度快、寿命长的优点，所以磁悬浮技术在实际中取得了广泛的应用。磁悬浮系统为非线性开环不稳定系统，对其控制方法的研究非常具有典型意义［1］。磁悬浮球系统作为研究磁悬浮特性，掌握其相应建模与控制方法的研究对象，在学习与研究中得到了广泛应用［2］。由于磁悬浮系统的非线性以及外部干扰引起的不确定性，很难建立准确的系统模型，因此，对于系统的非线性部分，采用非线性系统线性化的方法达不到想要的效果。现阶段，磁悬浮系统的非线性控制方法的研究得到了广泛的研究，如自适应控制、鲁棒控制等，都在一定程度上对磁悬浮系统的非线性部分有相应的控制作用［3］。

此外，滑模变结构控制算法也是一种有效的控制方法，它最大的优点是对系统参数波动和外扰动具有良好的鲁棒性，文献［4］中体现了这一点。但一般传统滑模变结构控制具有不连续性的缺点，导致其在实际控制中有严重的抖振，如何减小控制系统所引起的抖振，是目前研究的重点课题。针对此种问题的出现，文献［5］中将模糊控制与滑模控制结合应用于磁悬浮球系统中，有效地降低了抖振。文献［6］中采用的二阶动态滑模控制方法，文献［7］提出的趋近律滑模控制方法，文献［8］的神经网络滑模控制方法，都在一定程度上减少了系统的抖振情况，但是都没有考虑系统的不确定性及外加干扰。文中设计的自适应反演滑模控制器，考虑了实际控制中的情况，能更好地使磁悬浮球系统应用于实践中。文中将自适应反演滑模控制律应用于磁悬浮球系统的仿真分析与实时控制，控制器实现容易，并能确保系统的稳定性与动态性能。实验结果表明该方法具有较好的动态跟踪性能，并能有效的降低滑模控制给系统产生的抖振。

1　磁悬浮球系统的建模与分析

1.1磁悬浮球系统的工作原理

磁悬浮球系统结构如图1所示，主要包括电磁铁、传感器、控制部分、驱动部分、小球等。

系统的工作原理：首先采用位置传感器检测出小球位置的变化，然后通过AD转换器将模拟的位置信号转换为数字信号传给自适应反演滑模控制器，控制器根据已经设定好的控制律输出相应信号，信号经过 H桥驱动电路，改变线圈中的电流，进而改变小球所受的电磁力。最终使小球回到平衡位置。系统采用闭环控制，就能实时地改变电磁力的大小，保证小球处于平衡位置，从而使小球稳定的悬浮。

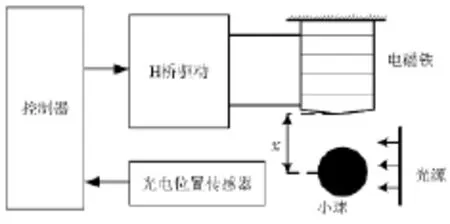
图1　磁悬浮球系统的系统结构图Fig．1　The structure diagram of the system

1.2磁悬浮球系统的数学模型

研究图1所示的磁悬浮球系统，在只考虑气隙磁通均匀，忽略铁心磁阻、漏磁及涡流损耗等情况下，小球受到的力可表述为

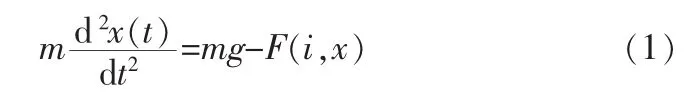
此外，对系统进行机理分析，可得系统的电磁力方程：

电学方程：

边界方程：

其中F为电磁吸力，i为线圈电流，m为小球的质量，g为重力加速度，L为线圈电感，R为线圈电阻，A为铁芯面积，N为线圈匝数，空气磁导率μ0=4π×10-7H/m。U（t）为电磁铁线圈绕组中的电压，x为小球的高度，此外，i0和x0分别为系统平衡时线圈电流和小球的高度。

由式（2）可知，此系统是非线性的。将其在平衡位置处进行线性化，即将式（2）进行泰勒展开并忽略二阶项，可得小球的运动方程为

选取状态变量x1=x，x2=x，则磁悬浮球系统的状态空间数学模型为

1.3磁悬浮球模型的数值化

本实验系统实际的物理参数如表1所示。

表1　磁悬浮球系统的物理参数Tab.1　The physical parameters of magnetic levitation ball system

系统的最终状态方程为：

2　自适应反演滑模控制器的设计

考虑到实际控制中，系统参数的不确定性及存在外加干扰，可以把式（6）写成如下形式：

假设参数不确定部分及外加干扰项变化缓慢，取

假设位置指令为xd，跟踪误差为e1=x1-xd，则

定义Lyapunov函数

定义x2=e2+xd-c1e1，其中c1为正的常数，e2为虚拟控制项，e2=x2-xd+c1e1，则

定义切换函数为

其中，k1＞0。

由于e1=e2-c1e1，则

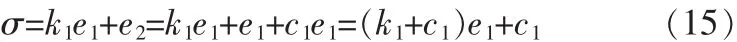
由于k1+c1＞0，显然，如果σ=0，则e1=0，e2=0且V1≤0。为此，需要进行下一步设计。

定义Lyapunov函数

则

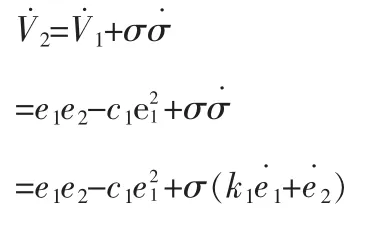
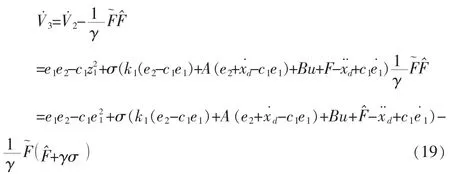
设计自适应控制器为

其中，h和β为正的常数。

设计自适应率为

将以上两式带入，得

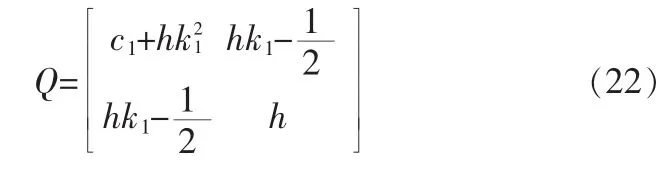
由于

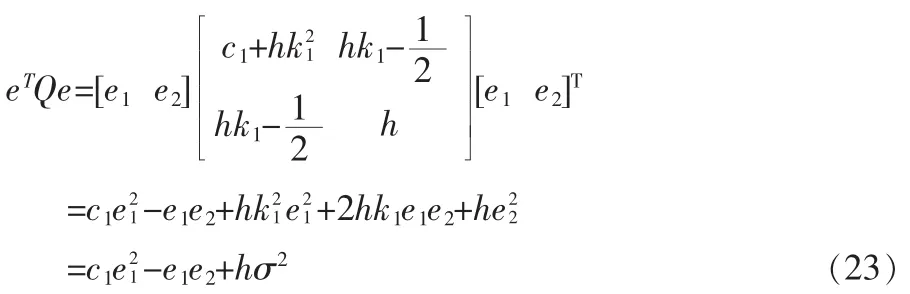
其中，eT=［e1e2］。

将（23）代入，V˙3可写为

如果保证Q为正定矩阵，有

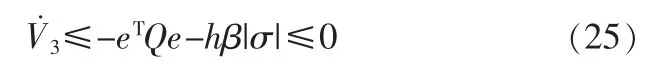
由于

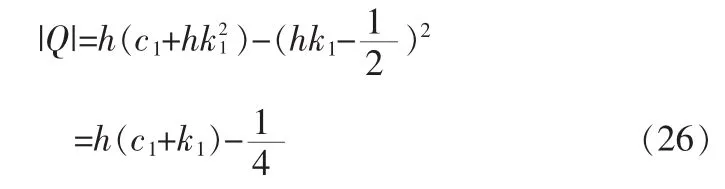
通过取h、c1和k1的值，可使|Q|＞0，从而保证Q为正定矩阵，从而保证V˙3≤0。

3　系统仿真

由式（7）和式（8）可知，A=2 000．9、B=-9．804 4。取F（t） =-3sin（0．01t），位置指令取xd=sint。取c1=100，k1=150，h=200。仿真结果为图2至图4。

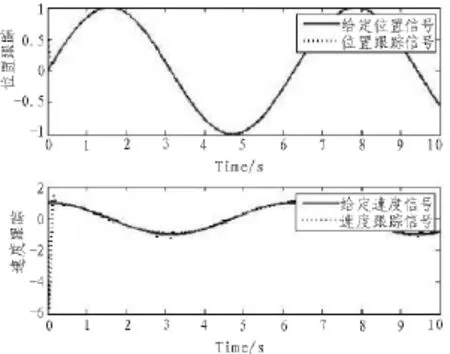
图2　位置和速度跟踪Fig．2　The position and velocity tracking

图3　控制输入Fig．3　Control input

通过图2可以看出，文中所设计的控制器对位置和速度跟踪比较精确，图4表明所设计的控制器可使输出响应有着较小的超调量与较快的响应时间，且在稳定状态下无稳态误差。

图4　控制输出Fig．4　Control output

4　结　论

文中设计了一种磁悬浮系统的自适应反演滑模控制器。与普通的滑模控制器相比，有效地减小了系统的抖振，与鲁棒反演滑模控制相比，更具有实际意义。因为鲁棒反演滑模控制对于总的不确定性的上界已知的情况下设计的。然而，在实际控制中，不确定性及外加干扰通常是未知的。在接下来的工作中，将进一步减少系统的理想条件进行研究，使设计的控制器能更好的应用于实践中。

［1］张耿．基于超导的磁悬浮列车磁悬浮系统的设计与分析［D］．长沙:国防科技技术大学，2007．

［2］俞坚才．人工心脏磁悬浮系统的开发［D］．浙江:浙江大学，2013．

［3］Elgammal A T．Fuzzy logic-based gain scheduling of Exact FeedforwardLinearizationcontrollerformagneticball levitation system［C］//Control（CONTROL），2014 UKACC International Conference on．Loughborough，UK:IEEE， 2014:531-536．

［4］Al-Muthairi N F，Zribi M．Sliding mode control of a magnetic levitation system［J］．Mathematical Problems in Engineering，2004，2004（1）:93-107．

［5］秦红玲，李志雄，袁松．磁悬浮轴承系统的模糊滑模变结构控制研究［J］．计算机仿真，2011，28（4）:185-188．

［6］黎恒，肖伸平．磁悬浮球系统的滑模变结构鲁棒控制器设计［J］．湖南工业大学学报，2014，28（1）:58-61．

［7］宋荣荣．单电磁铁悬浮系统的指数趋近律滑模控制［J］．重庆理工大学学报，2012，26（1）:11-16．

［8］赵石铁，高宪文，车昌杰．基于RBF神经网络的非线性磁悬浮系统控制［J］．东北大学学报，2014，35（12）:1673-1677．

Adaptive back-stepping sliding mode control of magnetic levitation ball system

ZHENG Jian-ying，YU Zhan-dong
（Bohai University，Jinzhou 121013，China）

Magnetic levitation ball system is a typical open-loop and unstable system，in order to achieve precise control of the magnetic levitation ball system，and make the system more practical，we design an adaptive back-stepping sliding mode controller．In the actual control system，uncertainties and external disturbances are unknown，we base on the practical application of this system，use a linear model of the system，to design the controller．The results show that:compared with the normal mode controller，the design of adaptive back-stepping sliding mode controller can reduce chattering of the system，can better achieve a stable suspension of the ball and has good dynamic tracking performance，and compared to the adaptive sliding mode controller，the controller we design in this paper can better applied in practice．

magnetic levitation ball system；sliding mode control；adaptive；back-stepping

TP13

A

1674－6236（2016）02-0076-03

2015-03-15稿件编号：201503195

郑建英（1990—），女，河北邢台人，硕士。研究方向：复杂系统运动控制。