基于GPU的受限玻尔兹曼机并行加速

张立民，刘 凯，范晓磊

（1．海军航空工程学院 山东 烟台 264001；2．第二炮兵工程大学 士官职业技术教育学院，山东 青州 262500）

基于GPU的受限玻尔兹曼机并行加速

张立民1，刘 凯1，范晓磊2

（1．海军航空工程学院 山东 烟台 264001；2．第二炮兵工程大学 士官职业技术教育学院，山东 青州 262500）

为针对受限玻尔兹曼机处理大数据时存在的训练缓慢、难以得到模型最优的问题，提出了基于GPU的RBM模型训练并行加速方法。首先重新规划了对比散度算法在GPU的实现步骤；其次结合以往GPU并行方案，提出采用CUBLAS执行训练的矩阵乘加运算，设计周期更长、代码更为简洁的Tausworthe113和CLCG4的组合随机数生成器，利用CUDA拾取纹理内存的读取模式实现了Sigmoid函数值计算；最后对训练时间和效果进行检验。通过MNIST手写数字识别集实验证明，相较于以往RBM并行代码，新设计的GPU并行方案在处理大规模数据集训练上优势较为明显，加速比达到25以上。

受限玻尔兹曼机；GPU；CUDA；加速比；并行加速

基于能量模型的受限玻尔兹曼机 （Restricted Boltzmann Machine，RBM）［1］以其简单的人工神经网络形式和快速的学习算法，越来越受到机器学习的关注，目前已经广泛应用于数据降维、语音识别、3D物体识别、图像转换以及高维时间序列建模等机器学习问题，进而催生出机器学习一个新的领域，深度学习［2］，并使之得到了迅猛发展。

但随着大数据时代的到来，模型训练需要的数据越来越多，单纯通过CPU进行计算已经逐渐失去优势，自2008年Paprotski等人研究了通过CUDA对RBM训练的加速方法［3］，并且取得了较好效果之后，利用GPU的高速运算能力以加快RBM训练，从而构建深度学习模型，已经成为了RBM训练的研究热点［4-6］。目前RBM的CUDA加速方法主要体现在两种方式，一种是基于相对成熟的CUDA并行库，例如CUBLAS库，另一种是根据RBM结构特点和训练步骤设计Kernel函数，对于RBM训练过程中目标不同的矩阵运算定义不同的Block和编写Kernel函数。第一种方法的优点在于，加速方式较为通用，不仅适用于RBM训练，还可应用于其他与矩阵运算相关的模型训练；代码运算稳定，较为健壮，不容易出现溢出问题；但是缺点在于针对性不强，不能高效利用GPU计算资源；第二种方法的优点是能够针对RBM模型，加速比好，但是缺点为设计较为复杂，扩展性不强。因此，设计一种能够结合两种方式的RBM并行加速方法，既保证算法的有效性，也使得扩展性增强。

1　受限玻尔兹曼机

1.1受限玻尔兹曼机模型

玻尔兹曼机 （Boltzmann Machine，BM）是 1985年由Hinton等提出的一种起源于统计物理学的随机递归神经网络。作为一种随机生成的Hopfield网络，BM由可见层和隐单元层组成，用可见单元和隐单元来表示随机网络和随机环境的学习模型，通过权值表示单元之间的相关性。

为克服BM训练时间过长、难以确切计算模型分布等问题，研究人员设计了受限玻尔兹曼机。RBM通过限制BM中的层内单元连接，使得在给定同层单元状态下临近层单元激活概率条件独立，其结构如图1所示。作为无向图模型，RBM中的V为可见单元层，表示观测数据；H表示隐单元层，表现为特征检测器，层内隐单元状态组合等价于观测数据的特征组合。文献［7］指出RBM的隐单元和可见单元可为任意指数族，如泊松单元、高斯单元和Sofmax单元等。文献［8］从理论方面对RBM的数据泛化能力进行了证明，得出了在足够多数目隐单元的情况下RBM可以表征任意离散分布的结论。

图1　RBM单元连接图Fig．1　RBM unit connection diagram

以包含N个二值可见单元和M个二值隐单元的RBM为例，设定vi表示第i个可见单元的状态，hj表示第j个隐单元状态。给定状态（v，h），模型的能量定义如式（1）所示。

其中，Wij表示可视单元i与隐单元j之间的连接权值，bi表示可视单元i的偏置，cj表示隐单元j的偏置，则RBM处于状态（v，h）的概率如式（2）所示。

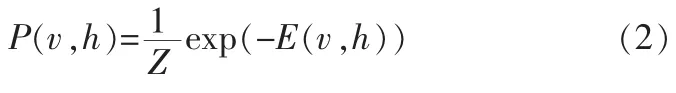
由于层间单元是无连接的，所有单元的激活状态都是条件独立的，则隐单元和可见单元的后验激活概率，如式（3）、（4）所示。

其中σ（x）=1/（1+exp（-x）），在本文中也写为Sigmoid函数。

1.2CD算法

RBM通过极大似然法则对数据进行无监督学习，即最大化训练数据出现概率。假设训练样本个数为K，则RBM对数据的学习即为最大化以下目标函数，如式（5）所示。

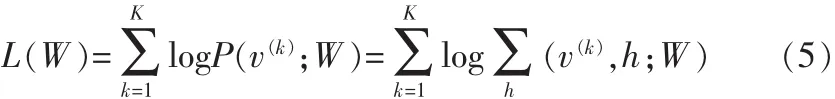
利用随机梯度下降法，目标函数式（5）对于各个参数的偏导如式（6）所示（以W为例）。

对于式（6）等号右侧多项式中的第一个项（Positive Phase），可以通过训练数据与式（4）直接计算出来；但是对于第二个项（Negative Phase），由于p（v．h）是无法直接通过数学推导出来的，故难以直接计算。

Hinton于2002年提出了对比散度（Contrastive Divergence，CD）算法［9］，通过执行吉布斯块采样（block Gibbs Sampling）—分别以各个训练数据作为初始状态，进行k次状态转移（k次Step），然后将转移后的数据作为样本对Negative Phase估算均值实现RBM的训练。Hinton通过实验证明，在实际应用中，甚至只需要一次状态转移就能保证良好的学习效果。由此，在给定训练数据 v（n）下，隐单元 j的特征 wj的迭代如式（7）所示。

2　CUDA实现

随着显卡技术的发展，最初用于计算机图形渲染的图像处理器 （Graphics Processing Unit，GPU）计算功能越来越强大，NVIDIA公司推出了面向通用计算的 CUDA（Compute Unified Device Architecture）运算架构［10-14］，已经成功地应用到了多种计算领域。

2.1算法分析

以Step=1的CD算法为例，对RBM在训练过程中的CUDA优化阶段进行分析，设定可见单元和隐单元维数分别为I和J，N为训练样本数目，以箭头表示RBM中参数参与计算的方向，则RBM的训练步骤如图2所示。

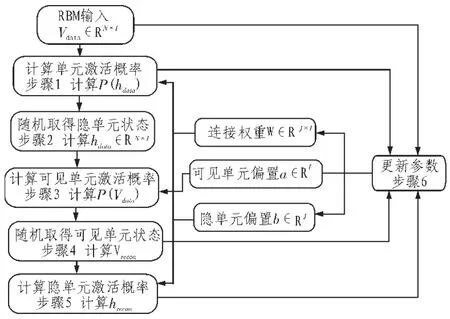
图2　RBM训练算法的步骤表示Fig．2　RBM algorithm training Steps

从图中可以看出，RBM的训练主要体现在步骤1～6中。这6个步骤分为矩阵乘加（步骤1、3、5、6）、0～1均匀分布随机数产生（步骤2、4）和Sigmoid函数计算（步骤1、3、5）3个方面。这3个方面计算要求不同，因此在设计CUDA并行化时需要单独对待。

2.2并行设计

1）矩阵乘加

鉴于矩阵运行库CUBLAS在处理矩阵运算的高效性和通用性，因此这一部分计算可以直接通过该库实现，主要使用库中处理双精度矩阵乘法运算的cublasDgemm函数。函数说明如下所示，并且所代表的运算如式（8）所示。

cublasDgemm（handle，CUBLAS_OP_N，CUBLAS_OP_N，mat1-＞_rows，mat2-＞_cols，mat2-＞_rows，&alpha，d_a，mat1-＞_rows，d_b，mat2-＞_rows，&beta，d_c，mat1-＞_rows）

其中 d_a为矩阵 a（mat1）在显存的地址，d_b为矩阵b（mat2）在显存的地址，d_c为计算结果c的地址，需要在计算完成以后复制到计算机内存中。

2）0～1均匀分布随机数的产生

0～1均匀分布随机数的产生需要CUDA随机数生成器参与。所谓随机数生成器（Random Number Generator，RNG），是指能够产生随机数序列的软件、硬件或者二者的结合。CUDA 的RNG实质上是伪随机数发生器 （Pseudo Random Number Generator，PRNG），下面对常用的PRNG进行简单介绍。

1）线性同余生成器（Linear Congruence Generator，LCG）

线性同余生成器是应用较为广泛的一种伪随机数生成器，优点在于计算速度快、容易实现、便于移植等，它是利用数论中的同余运算来产生伪随机数的，其随机数递推公式如式（9）所示。

其中a为乘子，c为增量，M为模数，Xi为序列中的第i个数，Xo称为种子（Seed）。

2）Tausworthe序列发生器

Tausworthe序列发生器又称为移位寄存器序列发生器，其工作原理是通过寄存器进行位移操作，直接在存储单元中生成随机数，递推运算公式如式（10）所示。

其中（x0，X1，…，Xp-1）为初始值，p>q＞0为整数，Xi是二进制行向量，⊕是位运算符。但是由于Tausworthe序列存在较为严重的相关性，很少被单独使用，通常用于构建组合Tausworthe生成器。

3）组合发生器

组合发生器指将多个独立的发生器按照某种方式组合在一起以产生伪随机数，从而得到统计性能更好和周期更长的PRNG。目前CUDA中的随机数生成器通常是几种PRNA的组合，从而达到扩大生成器周期和摒弃单独PRNA中存在的统计学缺陷的目的。文献 ［11］提出一种混合LCG和组合Tausworthe的随机数产生器，周期为 2121，文献［6］进一步对RNG进行了改良，实现Tausworthe113和CLCG4的组合发生器，其周期达到2234。

鉴于 Tausworthe113较为复杂，采用 CLCG4和组合Tausworthe共同作为随机数生成器，周期约为 2210=121+89。其Kernel端核心代码如下。

3）Sigmoid函数计算

文献［5］指出，CUDA能够实现Sigmoid函数的方式有两种，第一种是通过CUDA提供的-expf（x）函数，定义Sigmoid函数；第二种是利用CUDA拾取纹理内存的读取模式为cudaReadModeNormalizedFloat时数值被映射到［0，1］区间的能力，选用第二种方式。

综上，利用CUDA实现RBM训练的过程如图3所示。

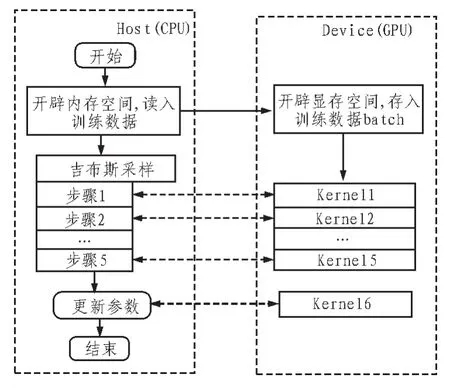
图3　基于CUDA的RBM训练并行设计Fig．3　RBM training CUDA-based parallel design

3　实验分析

为验证CUDA对RBM训练加速的效果，选取MNIST手写数字识别集为测试对象。通过对MNIST数据集进行训练，对比RBM的训练时间和对数据的拟合程度。实验平台的CPU为Intel Core i5 760@2．8GHz，主机内存4 GB，GPU采用GTX460（这与文献［5］的GPU平台一致，便于进行数据对比）。

CUDA优化性能主要参考的指标是加速比 （Speed-up）。加速比为程序串行执行时间与并行执行时间比值，数值越大，说明程序的并行化程度越高，CUDA优化效果越好，定义如式（1）所示。

实验设置RBM的结构为784-Nhid，其中Nhid代表隐单元个数分别取100至800的8个数值，RBM参数的学习速率统一设置为0．01，CD训练循环次数不超过1000。对比方法选用文献［5］提出的CUDA设计。图4为在不同隐单元个数下的两种CUDA设计的加速比值。

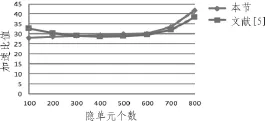
图4　不同CUDA方法加速比Fig．4　Speedup by different CUDA methods

从图中可以看出，经过CUDA加速，每个RBM的训练加速比都在25以上，表现出了较好的并行优化效率。当隐单元较少，即RBM结构小的情况下，所设计的CUDA加速与文献［118］相比存在差距，原因是Sigmoid函数计算中发生的对纹理内存的读取增加了显存读取，影响了计算效率。但随着隐单元个数的增大，所设计的CUDA程序能够得到更大的加速比，原因在于在CUDA框架下，所设计的CUDA程序对隐单元和可见单元随机状态的选取进行了硬件加速，相当于对RBM结构的参数更新进行了进一步的并行化设计。因此，随着隐单元个数的增大，其优越性将得到体现。

表1为当隐单元个数设置为800时，2种不同运算方式下的RBM训练时间。从表中可以看出，利用CUDA对RBM训练进行并行化计算，加速比达到41．32，说明所设计实现的CUDA并行化对RBM的加速较为有效。

选取不同训练样本个数下的CUDA对RBM的加速比如图5所示。

表1　RBM训练时间Tab.1　RBM training time

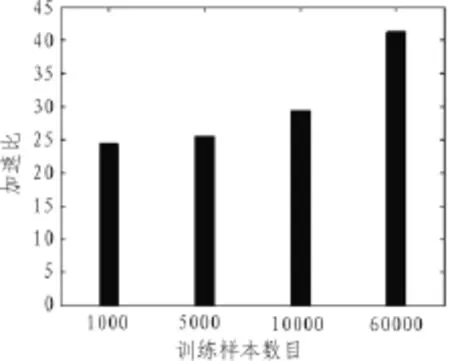
图5　不同样本数目下的CDBM加速比Fig．5　Speedup under different samples number

从图中可以看出，加速比基本与训练样本数目成正比，同时随着训练样本数目的增多呈现出更为显著的增长趋势。

4　结　论

本文设计了基于CUDA的RBM并行训练方法，实现了在GPU技术下RBM的加速训练。相对于以往RBM的并行加速训练，该方法能够更好地处理大规模数据，促进了RBM模型在未来大数据环境下的实用。从实验结果来看，本文设计实现的基于GPU的RBM并行加速实现，具有较广的应用范围和较高的工程价值。

［1］Becker S．An information-theoretic unsupervised learning algorithm for neural networks［D］．University of Toronto，1992．

［2］Srivastava N，Salakhutdinov R R，Hinton G E．Modeling documents with deep boltzmann machines［C］//29th Conference on Uncertainty in Artificial Intelligence．Bellevue:IEEE，2013:222-227．

［3］Daniel L．Ly，Paprotski V，Danny Y．Neural Networks on GPUs:Restricted Boltzmann Machines［C］//IEEE Conference on Machine Learning and Applications．Bellevue:IEEE，2010:307-312．

［4］CaiX，XuZ，LaiG，etal．GPU-acceleratedrestricted boltzmann machine for collaborative filtering［M］．Algorithms and Architectures for Parallel Processing．Springer Berlin Heidelberg，2012:303-316．

［5］Lopes N，Ribeiro B，Goncalves J．Restricted Boltzmann machines and deep belief networks on multi-core processors ［C］//Neural Networks（IJCNN），NewYork:Spring，2012:1-7．

［6］薛少飞，宋彦，戴礼荣．基于多GPU的深层神经网络快速训练方法［J］．清华大学学报：自然科学版，2013，53（6）:745-748．

［7］Welling M，Rosen-Zvi M，Hinton G E．Exponential family harmoniums with an application to information retrieval［C］．Advances in neural information processing systems，2004: 1481-1488．

［8］Le Roux N，Bengio Y．Representational power of restrictedBoltzmann machines and deep belief networks［J］．Neural Computation，2008，20（6）:1631-1649．

［9］G．E．Hinton．Training products of experts by minimizing contrastive divergence［J］．Neural Computation，2002，14 （8）:1711-1800．

［10］王坤．基于GPU的分类并行算法的研究与实现［J］．电子设计工程，2014，（18）:39-41．

［11］张聪，邢同举，罗颖，等．基于GPU的数学形态学运算并行加速研究［J］．电子设计工程，2011（19）:141-143．

［12］王应战，魏衍君．基于并行计算的木马免疫算法研究［J］．电子设计工程，2012（16）:45-47．

［13］荣少巍．基于改进A*算法的水下航行器自主搜索航迹规划［J］．电子科技，2015（4）:17-19，22．

［14］蒋磊，邹兵，吴明．基于改进免疫遗传算法的含分布式电源配电网规划［J］．陕西电力，2012（10）:26-30．

Realization of RBM parallel training based on GPU

ZHANG Li-min1，LIU Kai1，FAN Xiao-lei2
（1．Naval Aeronautical and Astronautical University，Yantai 264001，China；2．Noncommissioned Officers Vocational and Technical Education College，The Second Artillery Engineering University，Qingzhou 262500，China）

In order to overcome the low efficiency of Restricted Boltzmann Machine handle large data，on the basic of parallel computing platform GPU，the realization of RBM training based on GPU is designed．By researching the training steps of RBM，the contrast divergence algorithm is redesigned to implement on GPU．Combined with previous GPU parallel solutions，matrix multiply-add operations are implemented by CUBLAS libraries．The combination of Tausworthe113 and CLCG4 is used as random number generation to get longer cycle and more concise random number．The CUDA pickup texture memory read mode is used to achieve sigmoid function value，and finally The MNIST handwriting digit database is conduct on the test of this new realization．The MNIST experiment results illustrated that the novel algorithm has good feasibility and is advantageous for hug amount of data．Compared to the previous RBM parallel code，this new GPU parallel processing have more obvious advantages on large data sets and the speedup rate reach at least 25．

RBM；GPU；CUDA；speed-up；parallel programming

TN99

A

1674－6236（2016）02-0028-04

2015-03-21稿件编号：201503294

国家自然科学基金（61032001）

张立民（1976—），男，吉林开源人，博士，教授。研究方向：信号与信息处理、军用仿真技术。