高速公路改扩建成本预测的灰色-马尔可夫链模型

王军艳，李珏

（长沙理工大学交通运输工程学院，湖南长沙 410004）

高速公路改扩建成本预测的灰色-马尔可夫链模型

王军艳，李珏

（长沙理工大学交通运输工程学院，湖南长沙 410004）

高速公路改扩建过程中会受到众多因素的影响。文中结合其特点，在统计高速公路改扩建成本历史数据的基础上，建立灰色GM（1，1）预测模型，对高速公路改扩建成本进行预测，同时根据马尔可夫链模型对预测值与实际值之间的残差幅度进行状态分类，得出状态转移矩阵和预测区间值，最终求得各个序列的修正值，并通过实例说明了灰色-马尔可夫链预测模型的精度。

工程管理；高速公路改扩建；成本预测；灰色-马尔可夫链

高速公路改扩建项目的规划、设计、招投标、施工等阶段都存在影响建设成本的因素，为了有效控制高速公路改扩建成本、合理利用资源，需对高速公路改扩建进行成本预测和分析。目前关于改扩建工程成本预测的研究有：杨敏利用灰色GM（1，1）模型对改扩建项目成本进行预测，以得到的预测值和发展系数作为从实施过程备选方案预测指标结果中选择利益最优实施方案的衡量标准，使结果的可信度增加；张健等对改扩建项目投资决策问题进行分析，将AHP法和模糊评判法相结合，在价值工程的基础上建立了改扩建投资决策模型；左光文将一元回归方法用于工程项目成本预测，解决了在资料不够详实、时间较紧迫的情况下无法对工程项目成本进行预测的问题；雷剑从影响高速公路改扩建工程的各项经济技术指标出发，在模糊重构优化DEA的基础上建立了高速公路改扩建方案评价指标体系；陆红梅等运用模糊模式进行识别和选取，通过BP神经网络对工程项目成本进行预测，经过实例验证，得出基于这两种方法的模型可用于工程项目成本预测；刘颖等利用灰色理论方法对高速公路改扩建成本进行了预测，但只预测了未来几年高速公路扩建成本趋势，没有进行精度上的改善。该文运用灰色GM（1，1）模型，通过对某地区2001—2014年高速公路改扩建中四车道改八车道成本数据的处理，预测近4年高速公路改扩建成本，结合马尔可夫链模型得出状态转移矩阵，并对GM（1，1）模型得出的预测值进行修正，以得出更加准确的预测成本值。

1　灰色-马尔可夫链模型的基本思想

灰色GM（1，1）预测模型是灰色系统理论的核心内容之一，是灰色预测模型中应用最广泛的模型，它具有所需样本少、计算简单等特点。不像回归模型和经验模型那样需要从影响高速公路改扩建成本的众多因素中筛选出主要影响因素，更不需要收集主要影响因素的具体数据，而是从高速公路改扩建成本自身出发，在收集成本历史数据的过程中寻找有用信息和发现其内在规律，建立灰色GM（1，1）模型进行预测。它要求高速公路改扩建成本历史数据经过处理后具有指数规律，但由于高速公路改扩建项目在实施过程中受环境影响较大，且具有作业面狭小、工点分散、功效低、施工组织和交通组织复杂等特点，利用历史数据进行累加生成的数据并不一定具有指数规律，可能会产生误差，通过累加生成的数据也可能增加模型的误差。

马尔可夫链是一个随机过程，该过程是从一种状态转移到另一种状态，根据其规律性形成转移概率，进而预测状态未来的发展方向。高速公路改扩建是一个工程量大、征地拆迁困难、通行不间断、工程变更多的动态系统过程，可将改扩建成本作为这一动态系统的特征向量。成本的变化是一个随机过程，而马尔可夫链可以对该过程进行描述。

根据上述两种模型的基本思想，可以将高速公路改扩建成本每年的变化看成一个灰色动态系统，在此基础上建立灰色GM（1，1）预测模型，预测高速公路改扩建成本变化的未来趋势。但由于高速公路改扩建过程中的随机波动性较大，灰色GM（l，l）预测模型只能预测数据总体发展趋势，并不能很好地揭示该过程的波动性。为此，运用马尔可夫链对灰色GM（1，1）模型预测出的高速公路改扩建成本结果进行修正，提高预测精度。

2　灰色-马尔可夫链模型的建立

2.1GM（1，1）模型

（1）设有原始数据序列［见式（1）］，它是一个在限制区间内进行变化，序列长度为n的随机序列。在获得原始数据的过程中会受到种种因素的影响，需使用累加、累减、求均值的方法对原始数据进行降噪处理，使其具有一定的规律性，带有一定的指数规律并呈现整体上升的趋势。累加公式见式（2）。

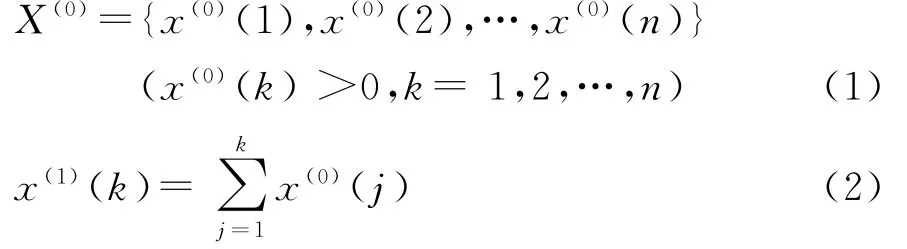
（2）根据x（1）（k）的指数增长规律，建立灰微分方程模型［见式（3）］，即灰微分方程的影子方程。

式中：x（1）为时间t的函数；a、b为待估参数。

（3）参数估计。设M=（a，b）T，待定，引入向量记号［见式（4）、式（5）］，将式（3）转换成离散形式，得Y=BM。通过MATLAB进行矩阵转换和最小二乘法计算参数M=（a，b）T，得式（6）。

式中：z（1）（k）=［x（1）（k-1）+x（1）（k）］/2，k=2，3，…，n。

（4）预测值的计算。将a、b值代入式（2），得到原微分方程的近似解［见式（7）］和离散响应量x（1）（k）的预测值［见式（8）］，进而得到X（0）的预测值［见式（9）］。

式中：x（0）（1）=x（1）（1）。

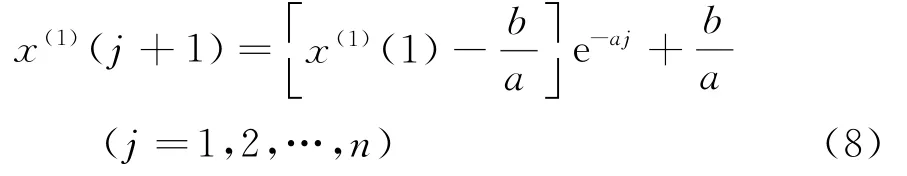
将灰色GM（1，1）预测模型的预测值与原始数据进行对比，得到两者在同一个时刻点的残差。

2.2马尔可夫链改进模型

鉴于灰色GM（1，1）预测模型的预测结果比较笼统，采用马尔可夫链对GM（1，1）模型预测结果进行修正，将预测结果限制在较小的区间，并通过状态转移矩阵使区间中的预测范围更加准确。

马尔可夫链是一个关于时间X（t）的随机过程，其基本思路是：在一个时刻T0状态S0已知的情况下，从状态S0转移到下一时刻T1的状态S1只与状态S0有关，而与T0之前的状态无关。运用马尔可夫链将同一时刻的预测结果和原始数据之间的残差程度进行状态分类，根据状态分类得出状态转移矩阵。一步状态转移矩阵形式为：

式中：Pij为由状态Si转移到状态Sj的概率，0≤。

Pij描述的是n个状态之间相互转移的概率。根据状态转移矩阵，可以对灰色GM（1，1）预测结果在一定的预测区间内进行修正，从而得出更加可信的预测值，提高预测结果的精度。

3　实例应用

某地区2001—2014年高速公路四车道扩宽为八车道的平均造价见表1。

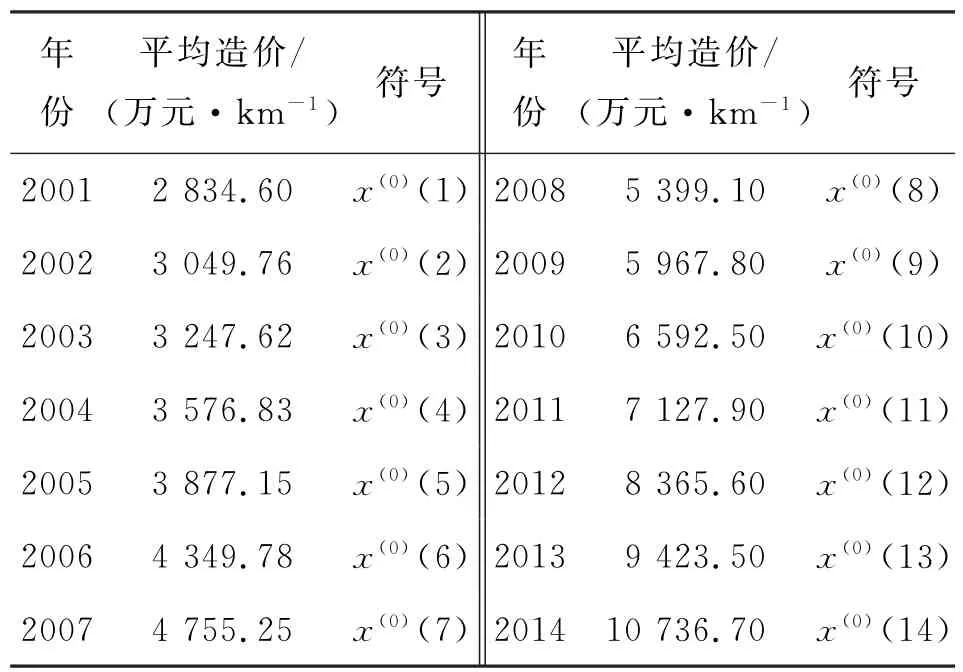
表1　高速公路四车道改八车道每公里平均造价

3.1模型建立

根据表1所示原始数据，经过数据变换处理后，建立灰色GM（1，1）模型对该地区高速公路四车道扩宽为八车道的平均造价进行预测。

（1）数据处理，建立原始数列：

将原始数据进行一次性累加，得出具有一定规律的数据序列：

（2）由式（4）～（6）求得B、Y；利用MATLAB进行矩阵运算，得a=-0.1099、b=2313.9。

（3）求出预测模型。将参数代入式（8），得到GM（1，1）模型：

利用该灰色GM（1，1）模型对2002—2014年高速公路改扩建成本进行预测，结果见表2。从表2可以看出：预测值与实际值之间的平均误差为1.28%（绝对值），最大年度误差为9%（绝对值），预测结果在可接受的范围内。

3.2状态划分

根据实际值与预测值的残差幅度进行状态分类，将高速公路四车道改八车道的平均造价划分为3种状态：状态1为高估状态，残差幅度为（-10%，-2%），从表2来看，2002、2003、2004、2014年为这种状态。状态2为正常状态，残差幅度为［-2%，2%］，2005—2010、2012、2013年为这种状态。状态3为低估状态，残差幅度为（2%，10%），2011年为这种状态。

根据以上状态分类结果，获得2002—2014年马尔可夫链的状态转移情况（见表3）。

表2　2002—2014年GM（1，1）预测结果

表3　2002—2014年灰色预测结果马尔可夫状态转移情况

根据表3得出2002—2014年马尔可夫链的状态转移矩阵：

根据状态转移矩阵得到之后4年（2015—2018年）的预测状态向量（见表4）。

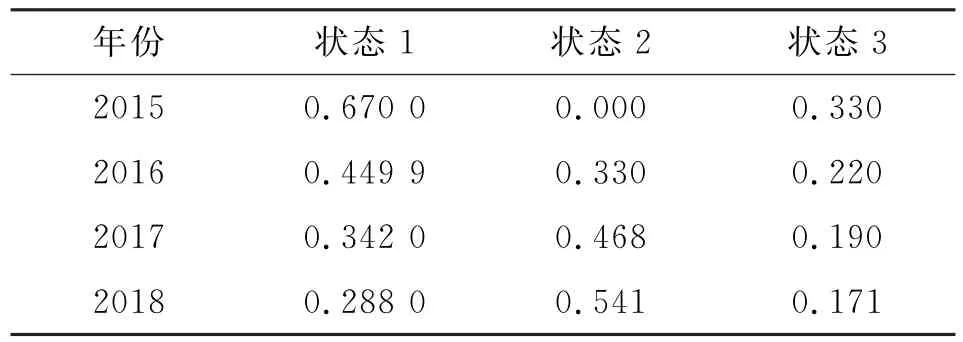
表4　2015—2018年灰色预测结果马尔可夫链状态向量

3.3近期高速公路改扩建成本预测

运用马尔可夫链模型对灰色GM（1，1）模型预测结果进行改进，结果见表5。

根据灰色GM（1，1）预测结果，该地区高速公路改扩建工程成本呈现逐年增长的趋势。采用马尔可夫链对灰色模型预测结果进行修正后，得出该地区高速公路改扩建成本处于高估状态，低于实际预测值。高速公路改扩建中要做好成本预测，使建设成本得到有效控制。

表5　基于灰色-马尔可夫链模型的高速公路改扩建成本预测结果

4　结语

高速公路改扩建过程属于一个在灰色系统前提下的随机过程，该文根据该特点，应用灰色-马尔可夫链模型对其成本进行预测。通过灰色GM（1，1）模型得出较为粗糙的预测值，然后利用马尔可夫链对预测值进行修正，得出状态转移矩阵，确定高速公路改扩建成本预测值位于不同区间的可能性，再将区间预测中值与通过状态转移矩阵得到的区间发生概率进行结合，更加准确地呈现高速公路改扩建成本发展总体趋势。灰色系统理论要求系统的影响因素相对稳定，故灰色-马尔可夫链模型适用于近期高速公路改扩建成本预测。

［1］ 杨敏.改扩建项目评估中经济效益评价的系统研究［D］.西安：西安建筑科技大学，2005.

［2］ 张健，郭剑峰，李慧民，等.基于价值工程的改扩建项目投资决策分析［J］.西安建筑科技大学学报：自然科学版，2007，39（5）.

［3］ 左光文.一元回归法在工程项目成本预测中的应用［J］.广东输电与变电技术，2009（1）.

［4］ 雷剑.高速公路改扩建工程精细化管理关键问题研究［D］.西安：长安大学，2011.

［5］ 陆红梅，王雪青.基于模糊模式识别和BP神经网络的工程项目成本预测模型研究［J］.项目管理技术，2013 （5）.

［6］ 刘颖，陈清廉，谈兴琦.基于灰色系统模型的高速公路改扩建成本预测［J］.工程建设，2015，47（5）.

［7］ 盖春英，裴玉龙.公路货运量灰色模型-马尔可夫链预测方法研究［J］.中国公路学报，2003，16（3）.

［8］ 梅振宇，王炜，李铭，等.高速公路交通生成预测的改进灰色马尔可夫模型［J］.公路交通科技，2004，21（12）.

［9］ GeetikaTLakshmanan，DavoodShamsi，YurdaerN Doganata，etal.Amarkovpredictionmodelfordatadrivensemi-structuredbusinessprocesses［J］.KnowledgeandInformationSystems，2015，42（1）.

［10］ 夏莉，黄正洪.马尔可夫链在股票价格预测中的应用［J］.商业研究，2003（10）.

［11］ 许晓燕.高速公路改扩建项目成本管理方法［J］.黑龙江科技信息，2012（16）.

［12］ 沈小庆，黄昕.基于熵权系数的医院建设项目风险评价［J］.项目管理技术，2014（1）.

［13］ 何雄伟，孙柏林，汪洋，等.高速公路施工标准化管理绩效评价研究［J］.交通标准化，2014（13）.

U415.13

A

1671-2668（2016）04-0272-04

2016-03-16