双重介质复合油藏偏心井试井分析

姜瑞忠，郜益华，孙召勃，何吉祥，李志涛（.中国石油大学石油工程学院，山东青岛66580；.中海石油（中国）有限责任公司天津分公司渤海石油研究院，天津30045）

双重介质复合油藏偏心井试井分析

姜瑞忠1，郜益华1，孙召勃2，何吉祥1，李志涛1
（1.中国石油大学石油工程学院，山东青岛266580；2.中海石油（中国）有限责任公司天津分公司渤海石油研究院，天津300452）

考虑到目前双重介质复合油藏直井试井的基本假设为井位于复合油藏内区中心，而在实际测试过程中很难保证井位于内区中心。采用偏心距描述复合油藏内区中偏心井所处的位置，建立了考虑表皮效应和井筒存储效应的复合油藏偏心井试井解释模型。利用点源理论、叠加原理、拉普拉斯变换得到了双重介质复合油藏偏心井的线源解，同时利用Stehfest数值反演获得实空间下的解，进而绘制了双重介质复合油藏偏心井的典型试井曲线，并分析偏心距对试井曲线的影响。研究结果表明，偏心距对复合油藏压力动态的影响主要体现在内区总体径向流与外区裂缝系统径向流间的过渡段，偏心距越大，内区总体径向流结束的时间越早，内区总体径向流与外区裂缝系统径向流间的过渡段出现得越早，过渡段压力导数曲线变化越缓慢。

双重介质；复合油藏；偏心距；偏心井；线源解；试井分析

国内外学者对多重介质复合油藏的试井问题进行了大量研究［1-9］。目前，双重介质复合油藏直井试井的基本假设仍是井位于内区中心［1，5，8-9］。然而由于地层复杂性和施工作业的影响，井位于双重介质复合油藏内区中心的理想情况很难出现。因此，对双重介质复合油藏偏心井的试井问题进行研究十分必要。文献［10］和文献［11］介绍了采用镜像反映法得到偏心井稳定产量公式的方法，文献［12］通过边界元方法，研究了均质油藏封闭边界条件下偏心井的不稳定产量变化规律。但对于双重介质复合油藏偏心井的研究非常少。本文应用点源理论得到了双重介质复合油藏偏心井的线源解和典型试井曲线，旨在为双重介质复合油藏偏心井的试井分析提供依据。

1　模型的建立与求解

1.1物理模型

双重介质复合油藏偏心井试井分析的物理模型如图1所示。模型的基本假设为:油藏厚度为h，具有双重介质特征，且介质间的流动为拟稳定流；油藏分为内、外两区，内区半径为r1，外区为无限大边界，内、外区具有不同的孔渗特性，内、外区裂缝系统和基岩系统的渗透率分别为Kf1，Kf2和Km1，Km2，内、外区裂缝系统和基岩系统的孔隙度分别为φf1，φf2和φm1，φm2，内、外区裂缝系统和基岩系统的压缩系数分别为Cf1，Cf2以及Cm1，Cm2；油井可视为线源，位于油藏内区任意位置，其位置用偏心距ra表示；考虑表皮系数和井筒存储系数的影响。

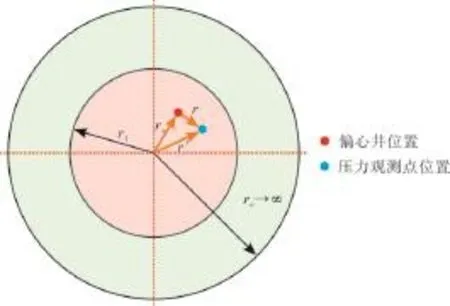
图1　双重介质复合油藏偏心井物理模型示意

1.2数学模型的建立与求解

对于双重介质复合油藏，偏心井开井生产后，其内、外区渗流微分方程分别为:

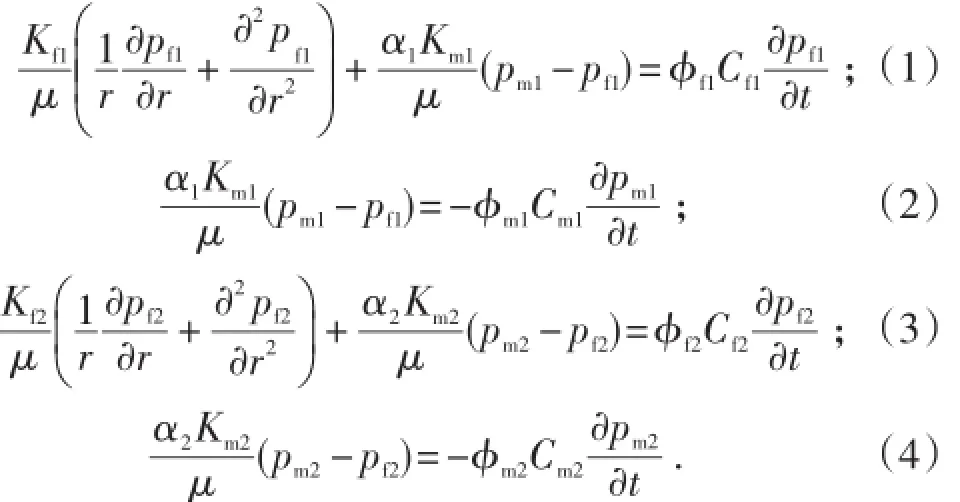
考虑偏心距后（图1），由余弦定理可得

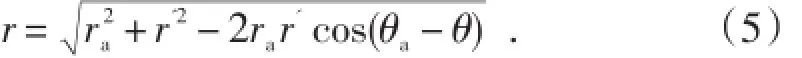
初始条件为

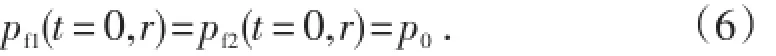
内区边界条件为

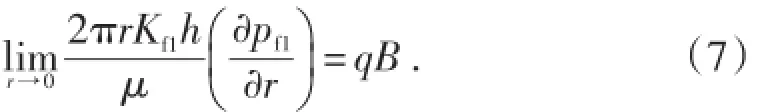
外区边界条件为

内、外区连接条件为

流量相等:

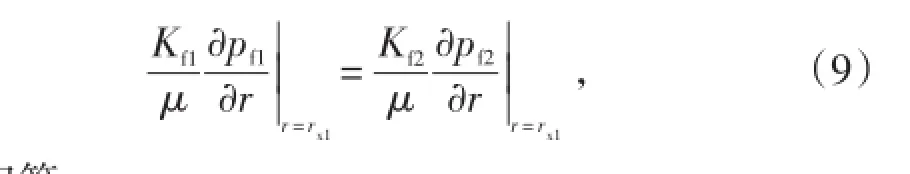
压力相等:

内、外区无因次压力: pf i D=2πKf1h（p0-pf i）/qμB，pm i D=2πKf1h（p0-pm i）/qμB.

无因次时间:tD=Kf1t/（φ1C1）m+fμrw2.

无因次半径:rD=r/rw.

无因次偏心距:raD=ra/rw.

无因次压力观测点半径:rD'=r'/rw.

无因次外区边界半径:re D=re/rw.

无因次外区边界距偏心井位置:rxe D=rxe/rw.

无因次内区边界距偏心井位置:rx1D=rx1/rw.

无因次地层厚度:hD=h/rw.

无因次z坐标:zD=z/rw.

内、外区储容比:β=（φ1C1）m+f/（φ2C2）m+f.

内、外区裂缝系统弹性储容比:

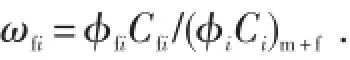
将上述无因次变量代入（1）式—（10）式并进行拉普拉斯变换，可得拉氏空间下的双重介质复合油藏偏心井模型为

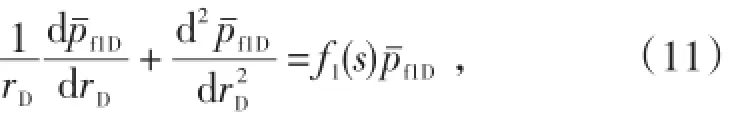
其中

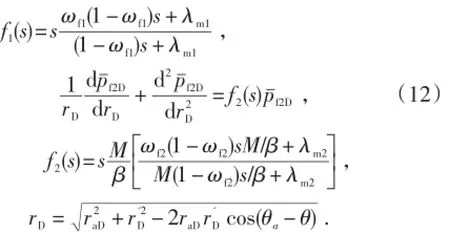
无因次内边界条件:

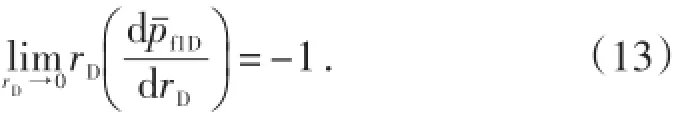
无因次外边界条件:

无因次内、外区连接条件:

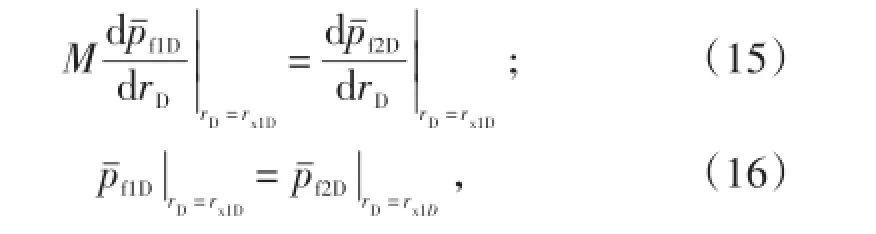
由叠加原理、点源理论［13-16］并结合虚宗量贝塞尔函数的性质［17］，可得双重介质复合油藏偏心井点源解。

偏心点源在油藏内区产生的压力分布为

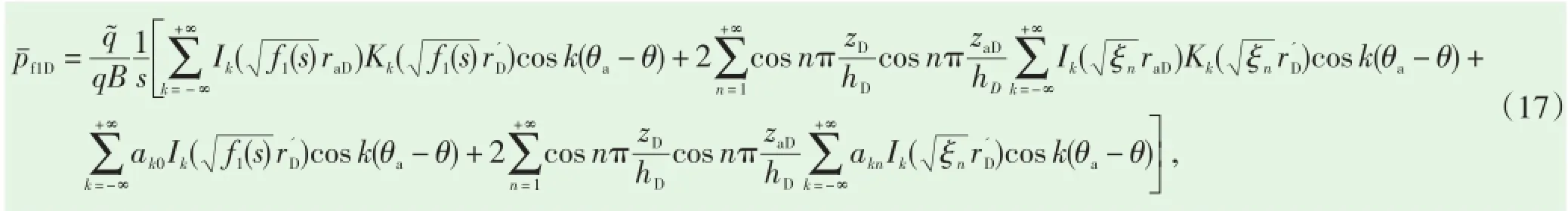
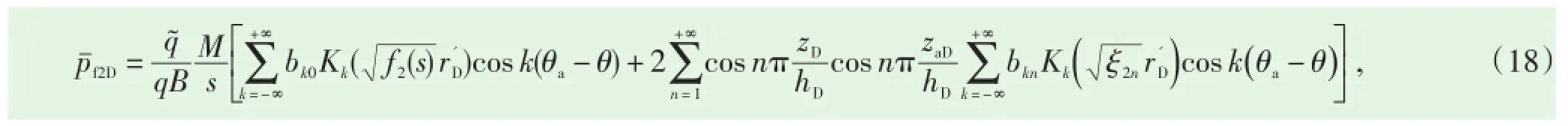
考虑内、外区连接条件（15）式、（16）式可得

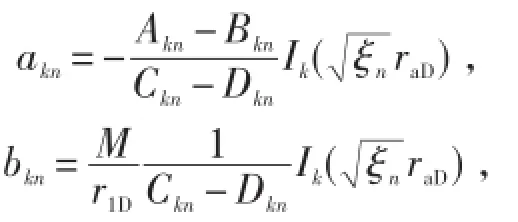
其中

对（17）式关于zaD从0到hD积分，可得双重介质复合油藏偏心井的线源解，即

为考虑井筒存储效应和表皮效应的影响，利用杜哈美原理［18］可得

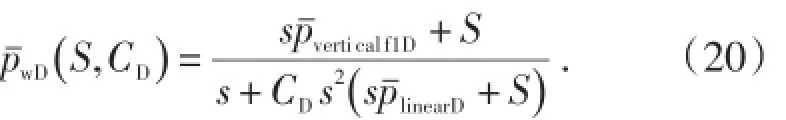
对（20）式采用Stehfest数值反演方法［18］进行反演，可得到双重介质复合油藏偏心井的井底压力解。

2　模型验证

为验证本文模型的正确性，令模型中偏心距raD= 0，从而得到井位于双重介质复合油藏内区中心时的解，并与常规的井位于内区中心的双重介质复合油藏试井模型［19］的解进行对比（图2）。

由图2可看出，当偏心距raD=0时，本文提出的双重介质复合油藏偏心井模型的解可以简化为经典的双重介质复合油藏试井模型解，二者所得结果完全相同，从而验证了模型的正确性。

3　典型图版分析

根据本文提出的模型，绘制双重介质复合油藏偏心井试井的典型曲线并与井位于内区中心（raD=0）的典型试井曲线进行对比，结果如图3、图4所示。

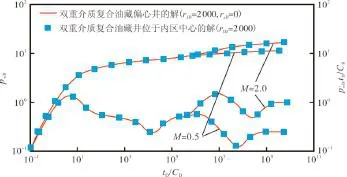
图2　双重介质复合油藏典型试井图版对比

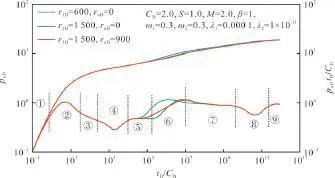
图3　 M=2.0时双重介质复合油藏偏心井典型试井曲线

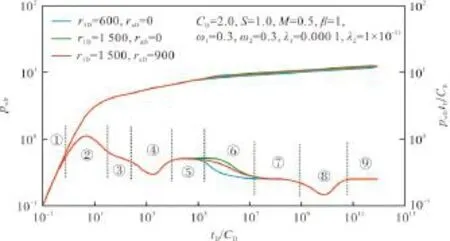
图4 M=0.5时双重介质复合油藏偏心井典型试井曲线

图3、图4分别给出了内区孔渗性好（M=2.0）、外区孔渗性好（M=0.5）时的双重介质复合油藏典型试井曲线的对比结果。图中的曲线分别为双重介质复合油藏不考虑偏心距（raD=0）时内区半径r1D=600和1 500以及考虑偏心距（raD=900）而内区半径r1D=1 500时的压力及压力导数曲线。由图3和图4可以看出，考虑偏心距后，双重介质复合油藏的流动阶段仍划分为9个阶段:①早期纯井筒存储阶段；②纯井筒存储阶段与内区裂缝系统径向流间的过渡段，此该阶段主要受表皮系数的影响出现“驼峰”；③内区裂缝系统径向流阶段；④内区基岩系统向裂缝系统窜流的过渡阶段，此阶段的特征为压力导数出现下凹；⑤内区裂缝系统和基岩系统总体的径向流阶段；⑥内区裂缝系统和基岩系统总体径向流与外区裂缝系统径向流间的过渡段；⑦外区裂缝系统径向流阶段；⑧外区基岩系统向裂缝系统窜流的过渡阶段，此阶段的特征为压力导数出现下凹；⑨外区裂缝系统和基岩系统总体径向流。分析图3、图4可知，偏心距的影响主要体现在内区总体径向流与外区裂缝系统径向流间的过渡段，偏心距的出现，会使得内区总体径向流提早结束，而内区总体径向流与外区裂缝系统径向流间的过渡段提前出现，同时过渡段的压力导数曲线变化也会变缓。

4　参数敏感性分析

图5、图6反映偏心距对双重介质复合油藏偏心井典型试井曲线的影响，偏心距越大，内区总体径向流结束越早，内区总体径向流与外区裂缝系统径向流间的过渡段出现的越早。这是由于偏心距越大，直井距内区边界的最小距离越小，压力开始传播到内区边界的时间越短，因而内区总体径向流结束的时间越早。另外，偏心距越大，过渡段压力导数曲线变化越缓慢。这是因为偏心距越大，过渡段中内区作用的时间越长，缓解了内、外区性质突变的影响，因而使得压力导数变化缓慢。

图6　 M=0.5时偏心距对双重介质复合油藏偏心井典型试井曲线的影响

5　结论

（1）本文基于点源理论得到了双重介质复合油藏偏心井试井模型的解析解，同时绘制了相应的典型压力图版。通过与经典的井位于内区中心的双重介质复合油藏试井模型的解进行对比，验证了偏心井试井模型的正确性。

（2）考虑偏心距后双重介质复合油藏的流动阶段可划分为9个阶段:早期纯井筒存储阶段；纯井筒存储阶段与内区裂缝系统径向流间的过渡段；内区裂缝系统径向流阶段；内区基岩系统向裂缝系统窜流的过渡阶段；内区裂缝系统和基岩系统总体的径向流阶段；内区裂缝系统和基岩系统总体径向流与外区裂缝系统径向流间的过渡段；外区裂缝系统径向流阶段，外区基岩系统向裂缝系统窜流的过渡阶段；外区裂缝系统和基岩系统总体径向流阶段。而偏心距的影响主要体现在内区总体径向流与外区裂缝系统径向流间的过渡段。

（3）对于双重介质复合油藏偏心井试井而言，偏心距越大，内区总体径向流结束越早，内区总体径向流与外区裂缝系统径向流间的过渡段出现得越早，过渡段压力导数曲线变化越缓。

符号注释

B——原油体积系数，m3/m3（标准状况）；

CD——无因次井筒存储系数；

Cfi——裂缝系统压缩系数，Pa-1；

Cmi——基岩系统压缩系数，Pa-1；

h——地层有效厚度，m；

Ik，Kk——k阶变形贝塞尔函数；

Kfi——裂缝系统渗透率，m2；

Kmi——基岩系统渗透率，m2；

M——内、外区流度比；

pfi——裂缝系统压力，Pa；

pmi——基岩系统压力，Pa；

p0——原始地层压力，Pa；

pw——井底压力，Pa；

q——偏心井地面标准状况下的产量，m3/s；

r——压力观测点距偏心井的位置，m；

r'——压力观测点距地层中心的位置，m；

r1——复合油藏内区半径，m；

ra——偏心距，m；

re——从油藏内区中心计起的外边界半径，m；

rw——井筒半径，m；

rxe——双重介质复合油藏外边界距偏心井的位置，m；

rx1——复合油藏内区边界距偏心井的位置，m；

S——表皮系数；

s——拉氏空间下的变量；

t——时间，s；

z——压力观测点纵向坐标，m；

za——偏心点源纵向坐标，m；

αi——与基岩形状有关的形状因子，m-2；

β——内、外区储容比；

ω——内、外区裂缝系统弹性储容比；

θ——压力观测点关于地层中心的极角，弧度；

θa——偏心井位置关于地层中心的极角，弧度；

μ——原油黏度，Pa·s；

φfi——裂缝系统孔隙度，f；

φmi——基岩系统孔隙度，f；

下标:

i——可取1和2，1为双重介质复合油藏内区，2为双重介质复合油藏外区；

m——基岩；

f——裂缝。

［1］黄霖，刘启国.多区双重介质复合气藏渗流数学模型及其压力动态［J］.油气井测试，2006，15（4）:11-14.

HUANG Lin，LIU Qiguo.Percolation mathematic model in compound gas reservoir with dual medium of excessive section［J］.Well Testing，2006，15（4）:11-14.

［2］赵海洋，贾永禄，王东权.双重-均质复合油藏产量递减模型研究［J］.新疆石油地质，2010，31（1）:63-65.

ZHAO Haiyang，JIA Yonglu，WANG Dongquan.Study of production decline model for dual porosity-homogeneous composite reservoir［J］. Xinjiang Petroleum Geology，2010，31（1）:63-65.

［3］陈方方，贾永禄.三孔双孔介质径向复合油藏模型与试井曲线［J］.油气井测试，2008，17（4）:1-4.

CHEN Fangfang，JIA Yonglu.The model of the trip le-double porosity radial composite reservoir and the type of curve［J］.Well Testing，2008，17（4）:1-4.

［4］陈方方，贾永禄，霍进，等.三孔均质径向复合油藏模型与试井样版曲线［J］.大庆石油学院学报，2008，6（6）:64-67.

CHEN Fangfang，JIA Yonglu，HUO Jin，et al.The flow model of the triple-medium composite reservoirs and the type curves［J］.Journal of Daqing Petroleum Institute，2008，6（6）:64-67.

［5］刘启国，冯宇，董凤玲.受界面附加阻力影响的双重介质径向复合油藏试井解释模型研究［J］.油气井测试，2005，14（3）:11-13.

LIU Qiguo，FENG Yu，DONG Fengling.Study on testing interpretation model of dual medium and radial compound reservoir influenced by interface addition friction［J］.Well Testing，2005，14（3）: 11-13.

［6］杨坚，姚军，王子胜.三重介质复合油藏压力动态特征研究［J］.水动力学研究与进展（A辑），2005，20（4）:418-425.

YANG Jian，YAO Jun，WANG Zisheng.Study of pressure-transient characteristic for trip le-medium composite reservoirs［J］.Chinese Journal of Hydrodynamics，2005，20（4）:418-425.

［7］向开理，李允，李铁军.不等厚分形复合油藏不稳定渗流问题的数学模型及压力特征［J］.石油勘探与开发，2001，28（5）:49-52.

XIANG Kaili，LI Yun，LI Tiejun.The mathematical model of unstable flow of fluids through porous media with non-uniform thickness lateral heterogeneity of fractal reservoir［J］.Petroleum Exploration and Development，2001，28（5）:49-52.

［8］郭建春，向开理.不等厚横向双重介质复合油藏试井分析模型及数值解［J］.油气井测试，1999，8（1）:1-5.

GUO Jianchun，XIANG Kaili.Well testing analysis model and numerical solution for a composite reservoir with non-uniform thickness and double media［J］.Well Testing，1999，8（1）:1-5.

［9］SATMAN A.Pressure-transient analysis of a composite naturally fractured reservoir［J］.SPE Formation Evaluation，1991，6（2）: 169-175.

［10］张建国，杜殿发，侯健，等.油气层渗流力学［M］.山东东营:中国石油大学出版社，2009:97-100.

ZHANG Jianguo，DU Dianfa，HOU Jian，et al.Oil and gas seepage mechanics［M］.Dongying，Shandong:China University of Petroleum Press，2009:97-100.

［11］葛家理，宁正福，刘月田，等.现代油藏渗流力学原理［M］.北京:石油工业出版社，2000:89-90.

GE Jiali，NING Zhengfu，LIU Yuetian，et al.The modern mechanics of fluid flow in oil reservoir［M］.Beijing:Petroleum Industry Press，2000:89-90.

［12］刘洪，王新海，任路，等.偏心井产量变化规律研究［J］.数值计算与计算机应用，2012，33（3）:159-166.

LIU Hong，WANG Xinhai，REN Lu，et al.Production change rules of eccentric well［J］.Journal on Numerical Methods and Computer Applications，2012，33（3）:159-166.

［13］OZKAN E，RAGHAVAN R.New solutions for well-test-analysis problems:Part 2-computational considerations and applications［J］. SPE Formation Evaluation，1991，6（3）:369-378.

［14］OZKAN E，RAGHAVAN R.New solutions for well-test-analysis problems:Part 1-analytical considerations［J］.SPE Formation Evaluation，1991，6（3）:359-368.

［15］OZKAN E.New solutions for well-test-analysis problems:Part 3-additional algorithms［R］.SPE 28424-MS，1994.

［16］GRINGARTEN A，RAMEY H J.The use of source and Green's function in solving unsteady-flow problems in reservoirs［J］.SPEJ，1973，13（5）:285-296.

［17］CARSLAW H S，JAEGER J C.Conduction of heat in solids（2nd edition）［M］.Oxford University Press，1959:376-378.

［18］KUCHUK F.Generalized transient pressure solutions with wellbore storage［R］.SPE 15671-MS，1986.

［19］同登科，陈钦雷.关于Laplace数值反演Stehfest方法的一点注记［J］.石油学报，2001，22（6）:91-92.

TONG Dengke，CHEN Qinlei.Some annotation about Stehfest method of Laplace numerical inversion［J］.Acta Petrolei Sinica，2001，22（6）:91-92.

［20］卢德唐.现代试井理论及应用［M］.北京:石油工业出版社，2009:211-216.

LU Detang.Modern well testing theory and its application［M］.Beijing:Petroleum Industry Press，2009:211-216.

（编辑叶良）

Off-Center Well Test Analysis for Composite Dual-Porosity Reservoirs

JIANG Ruizhong1，GAO Yihua1，SUN Zhaobo2，HE Jixiang1，LI Zhitao1
（1.School of Petroleum Engineering，China University of Petroleum，Qingdao，Shandong 266580，China；2.Bohai Oil Research Institute，Tianjin Branch，CNOOC，Tianjin 300452，China）

The basic assumption of formation test in composite dual-porosity reservoirs in vertical wells is that wells should be located in the center of the inner region of the reservoir.However，this assumption is hard to be realized during the actual well test.Eccentricity is used to describe well locations in the inner region of composite reservoirs，then an off-center well test model considering skin effect and wellbore storage is established for composite dual-porosity reservoirs.The line-source solution of the model is obtained on the basis of pointsource theory，superposition principles and Laplace transform，and the solution in the real space is acquired by Stehfest numerical inversion，based on which the typical pressure curves are further plotted and the influence of eccentricity on typical pressure curves is analyzed. The results show that the influence of eccentricity on the pressure performance of composite reservoirs is mainly embodied in the transition stage of radial flows between that in the inner region and the fracture system in the outer region.And a bigger eccentricity will lead to an earlier end of the inner-region radial flow of the whole system，the transition stage of radial flows will occur earlier，and the pressure derivative curve in the transition flow stage will change more slowly.

dual-porosity；composite reservoir；eccentricity；off-center well；line-source solution；well test analysis

TE353

A

1001-3873（2016）03-0327-05

10.7657/XJPG20160316

2015-12-26

2016-03-09

国家自然科学基金（51374227，51574265）；山东省自然科学基金（ZR2011EL034）；国家科技重大专项（2016ZX 05027004-004）

姜瑞忠（1964-），男，江苏溧阳人，教授，博士生导师，油气田开发，（Tel）18678967281（E-mail）jrzhong@126.com