基于粗糙集理论的灌区节水改造项目后评价模型

2016-09-13邵红艳浙江省金华市农村水利管理处浙江金华321000

水电站机电技术 2016年5期

关键词：约简粗糙集区分

邵红艳（浙江省金华市农村水利管理处，浙江金华 321000）

邵红艳
（浙江省金华市农村水利管理处，浙江金华 321000）

粗糙集理论运用到灌区节水改造项目评价中是切实可行的。

粗糙集理论；评价模型；灌区节水改造项目

1　灌区节水改造项目评价指标体系建立

在建立灌区节水改造项目后评价指标体系的时候，应该充分考虑工程实施对灌区的各种影响和节水改造的综合效益，以及影响综合效益的各种因素，建立一个科学的、完备的、可靠的指标体系。还需考虑指标之间的相互影响和依赖程度。如果指标B的完成或者完成程度是以A指标为基础的，那么只需考查A指标即可，不需要把2个指标同时纳入指标体系中。基于这样的考虑，指标体系不应该包含太多的指标。过于复杂、指标太多的评价指标体系不适合推广，同时过多的数据所产生的随机误差会对整个评价过程有不利的影响。

本文在参考水利部农村水利司《全国大型灌区续建配套与节水改造项目评估工作文件汇编》等文献的基础上，建立的指标体系包括：项目建设过程指标，项目效益指标，项目管理与改革指标、项目可持续性指标等4个一级指标。再将这4个一级指标继续划分为13个二级指标。具体指标体系见下页表1。

2　基于粗糙集理论的灌区节水改造项目评价模型

2.1评价模型指标信息表的设定

本文以10个灌区作为研究对象。为了构建评价模型，需要将灌区资料与指标体系汇总到一个信息表中［12］。汇总后的信息表格如下页表2所示。

上述信息表用S=＜U，R，V，f＞表示，其中：U是论域，U=｛x1，x2…，xn｝，表示对象的非空有限集合，灌区后评价中指的是样本灌区的集合；R是属性集合，R=｛r1，r2…，rn｝，表示所有指标的集合，一个属性对应一个指标，即一个等价关系，f：U×R→V，表示一个信息函数，它为每一个属性赋予一个信息值，即

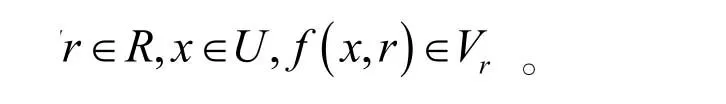
2.2评价指标连续属性离散化

粗糙集理论只能处理离散化的数据，所以还需将信息表中指标的连续属性进行离散化处理。本文通过采用模糊C均值聚类（Fuzzy C-Means Cluster，简称FCM）的方法对每一列的属性值进行聚类，聚类之后的类别编号作为离散化之后的特征值。用离散值”1“，”2“，”3“表示，”1“，”2“，”3“只表示类别，并不表示数值。

设X=｛x1，x2…，xn｝为n元数据集合，FCM算法把X划分为c个模糊子集S1，S2…，Sc。用z1，z2…，zc表示这c个模糊子集的聚类中心，uij表示元素xj对zi的隶属度，其中i=1，2，…，c，j=1，2，…，n。FCM算法的目标函数其中dij是xj与ci之间的距离，一般可用欧几里德距离；m＞1，是一个可以控制聚类结果的常数；且uij满足：…，n。可借助Matlab中的fcm工具箱和相关函数来完成FCM算法，将聚类结果中样本所属的类别序号作为它的离散化之后的特征值。

具体离散化结果见表3。

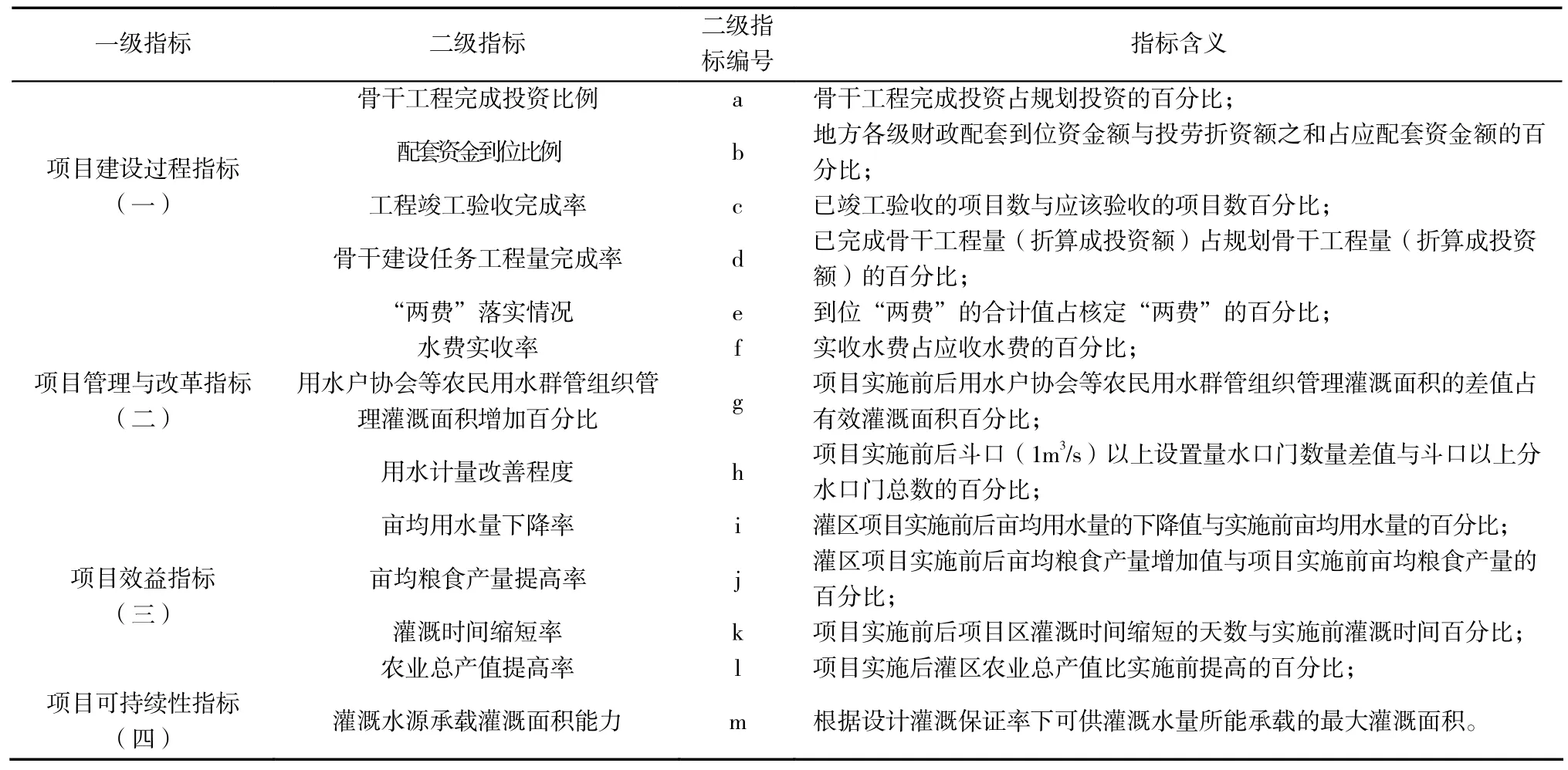
表1　评价指标信息表

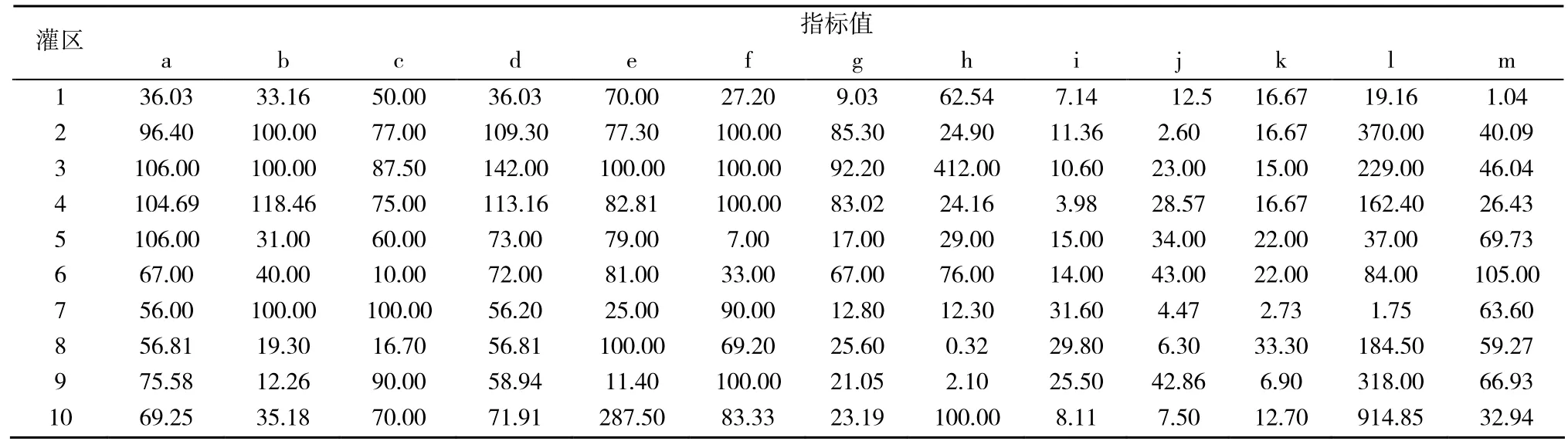
表2　评价模型指标值表

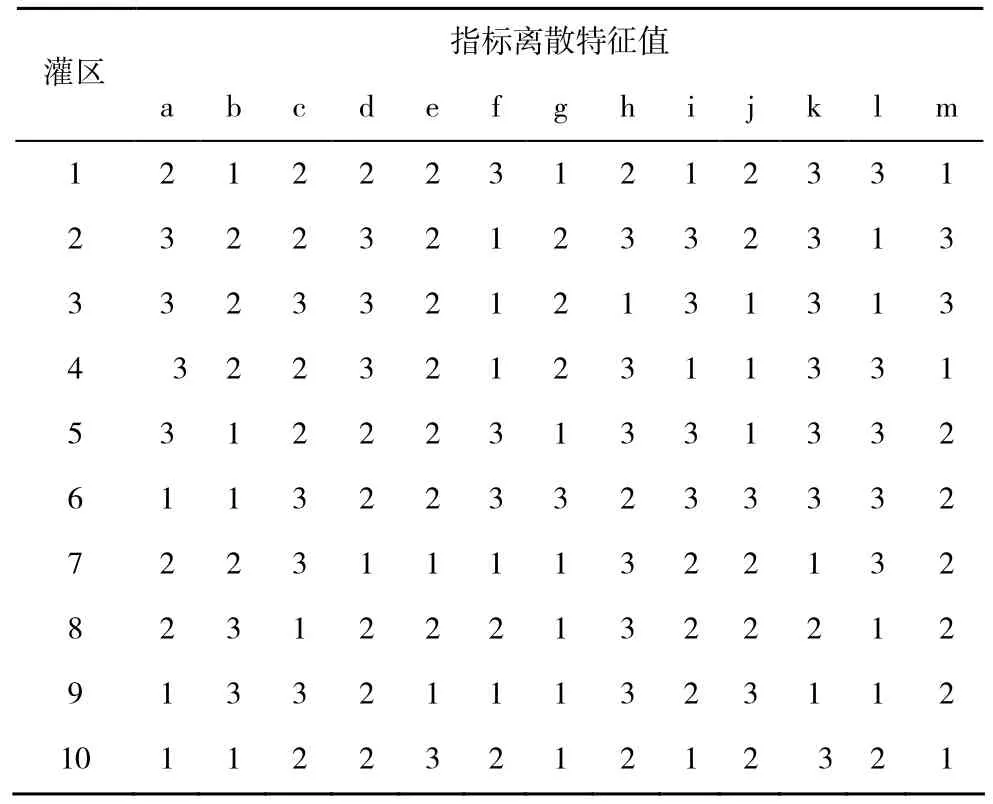
表3　评价模型指标离散特征值

2.3评价指标集约简

粗糙集可处理不精确、不确定和不完整的信息，通过约简方法可从大量数据中求取最小不变集合（核），去除指标集中的冗余指标。粗糙集可反映指标之间的依赖关系，因此可以对不同类型的指标进行区分，从中发现规律性知识，将不必要的、相对必要的、必要的指标进行区分，从而达到约简的目的。本文依据区分矩阵来约简指标集。构建区分矩阵和区分函数，应用吸收律对区分函数进行化简即可得到所有的约简集合。

在包含有n个评价对象和m个评价指标的信息系统S中，我们可构建区分矩阵。S对应的区分矩阵M是一个n×n的矩阵。Mij=｛r∈R|f（xi，r）≠f（xj，r）｝（i，j=1，2，…，n）。本文中的区分矩阵见表4。引入一个布尔函数，对每个属性r∈R，指定一个布尔变量r。若M≠Φ，则布尔函数为表示；若M=Φ，则布尔函数为1。所以区分函数f（r）=

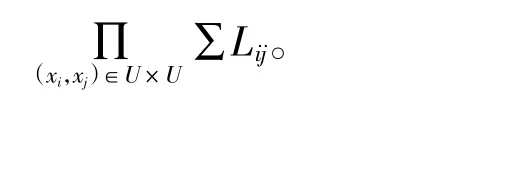
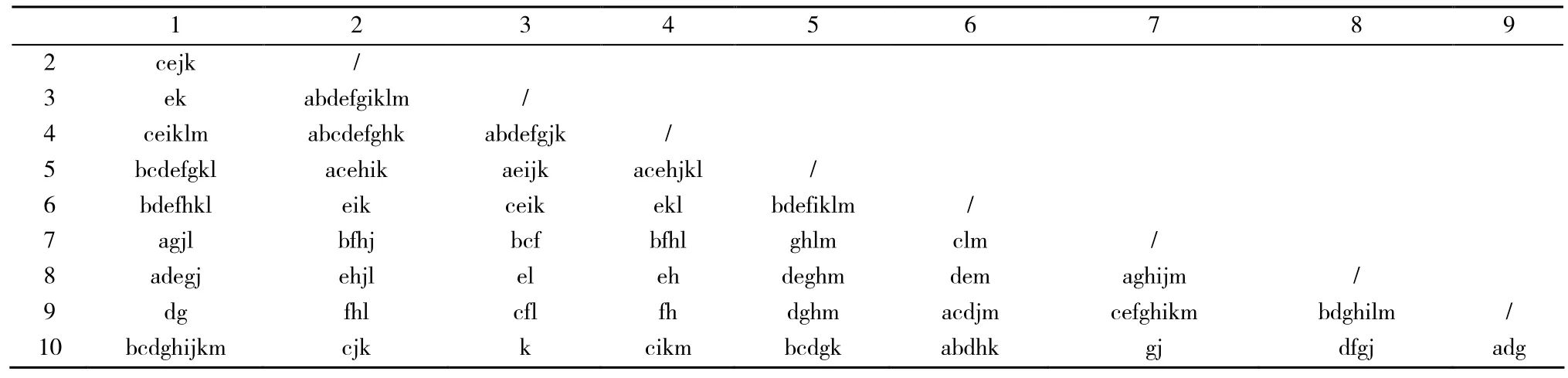
表4　区分矩阵

表5　约简结果

根据文献［13］中的方法，可大大节省对区分函数的化简时间。具体约简的指标集见表5，约简集的组合情况不止一种，在充分考虑评价指标的科学性、系统性、层次性、信息来源可靠性、实效性、可操作性等的基础上，选取第20个集合，即c，g，h，k，l，m为最后的约简指标集，这6个指标具有一定代表性，符合上述要求。

2.4评价指标权重的计算

经过属性约简后，得到约简指标集P=｛r1，r2，…，rm｝，由约简的定义可知，P中的属性都是必要的，但属性的重要度要根据粗糙集中运用知识信息量对属性的重要度进行计算，计算出各个指标的重要度SP（ri）（i=1，2，…，m）。但是基于属性重要度确定指标权重是基于等价关系的分类，但是等价关系的分类过细，可能会出现无法确定指标属性重要度的情况。因此，将等价关系扩充为模糊等价关系，从而放松分类的宽度，增大粗糙集的知识粒度［14-15］。如果要在模糊等价关系的基础上建立粗糙集，需要根据相似度λ的取值来确定模糊等价关系，根据陈懿伟等人的研究［16］，相似度λ的取值范围为［0.8，1］，λ的取值越大，则对论域U的划分则越详细。当λ分别取值为0.93，0.92， 0.90时所相对应的对论域的划分情况分别是9类，7类，6类。本文根据不同λ取值对论域U的划分情况，选取λ=0.93。

模糊等价关系P对论域U的划分为U/ind（P），模糊等价关系P的知识信息量是I（P）。去掉ri=c时，模糊等价关系P-｛c｝对论域U的划分为U/ind （P-｛c｝），相对应的模糊等价关系的知识信息量为I （P-｛c｝），则指标c的属性重要度SP（c）=I（P）-I（P-｛c｝）。

将以上各指标的属性重要度经过归一化处理之后即可得到各自的权重，具体结果见表6。根据表6的结果，h指标的权重最大，g、m次之。h、g指标反映的是项目的管理情况，m指标反映的是项目的可持续性，项目的管理情况和可持续性是项目顺利开展的基础和重要保证；合理、科学、高效的管理，具有可持续性，同样也是项目取得成果和效益重要基础。c指标反映的是项目过程，k、l指标反映的是项目效益。若是项目无法顺利开展，那么就更谈不上项目的过程和取得的效益，所以相对于前面3个指标来说c、k、l的权重较小。可见6个指标的权重大小合理，符合实际情况。