基于PID神经网络的平流层飞艇姿态控制研究

张一，刘龙斌

（北京航空航天大学 航空科学与工程学院，北京　100191）

基于PID神经网络的平流层飞艇姿态控制研究

张一，刘龙斌

（北京航空航天大学 航空科学与工程学院，北京100191）

针对平流层飞艇的姿态控制问题，阐述利用PID神经元网络结构对飞艇进行飞行控制率设计。首先，针对平流层飞艇运行特点建立了完整六自由度动力学模型，随后在模型基础上提出PID神经网络的组成结构和计算方法，并利用粒子群算法对神经元网络初始权值进行了优化。仿真计算结果表明，通过PID神经网络对控制率进行设计能够迅速接近控制目标，实现对平流层飞艇姿态的准确控制。

PID神经网络；平流层飞艇；姿态控制；粒子群算法

平流层飞艇属于一类轻于空气的飞行器，在通讯、侦查监视和科学探测方面有着广泛的应用前景。为了更好满足飞行任务对飞艇稳定姿态及精准指向等方面的要求，快速、准确、稳定的平流层飞艇姿态控制系统成为研究重点和关键。

目前应用于飞艇的控制方法包括经典控制和现代控制方法等。文献［1］基于简化的飞艇线性化模型设计了一种鲁棒PID飞艇姿态控制器，该控制器结合鲁棒极点配置技术能够保证闭环系统的响应性能。Acosta等［2］利用反馈线性化方法，为Titan飞艇设计了位置PD控制器和速度动态逆控制器。文献［3］基于线性化飞艇模型和反步法，设计了纵向运动控制器以控制飞艇的速度和俯仰角并给出了仿真结果。Trevino等［4］利用滚动时域控制 （Receding Horizon Control）方法对Tri-Turbofan遥控飞艇进行了稳定控制。

由于影响平流层飞艇姿态的干扰因素众多，传统的PID控制方法难以适应飞艇复杂的系统特性和飞行状态，而一些高精度的现代控制方法往往由于计算规模太大而又难以满足实时性要求。文中结合了传统PID控制器结构简单和响应快速以及神经网络适应性和鲁棒性强的特点，设计了一种应用于平流层飞艇姿态控制的PID神经网络控制器，该控制器的结构简单规范，易于实现，融解耦器与控制器于一体，使控制系统具有良好的动态和静态性能，适用于飞艇的姿态控制。

1　平流层飞艇动力学建模

飞艇数学模型与传统飞行器数学模型的建立方法相似，都是以动量、动量矩定理为基础进行建立的，但要比普通飞行器更加复杂［5］。本文所要建立的飞艇模型采用传统椭球体构型，飞艇有一纵对称面，尾翼采用“+”字形带升降舵和方向舵布局，吊舱位于艇囊下方，吊舱质心位于飞艇纵剖面内体心正下方，整个结构如图1所示。

1.1基本假设

为了简化模型，做出如下假设：建模时飞艇视为刚体；飞艇的形心与浮心重合；忽略地球自转和公转，设地球坐标系为惯性系；忽略地平面曲率，设地面为平面。

1.2受力分析

重力G和浮力B在地面坐标系下只存在竖直方向上的分量，利用坐标系转换矩阵可以将重力和浮力同时转换至艇体坐标系，由于艇体系原点选在体心，且假设体心与形心重合，因此浮力产生的对原点的力矩为零，即MB=0，只有重力产生力矩。

图1　平流层飞艇总体结构图Fig.1　Structure diagram of the stratospheric airship

式中：Rgb为从地面坐标系至艇体坐标系的转换矩阵；Src为重力作用点矩阵。

飞艇表面的气动压力可归结为作用于飞艇艇体坐标系的主矢和主矩。苗景刚［6］根据风洞试验数据对气动力及舵控制力进行了高精度的拟合，计算公式如下：

由于飞艇的体积重量比大，所以附加质量（惯量）的影响必须予以考虑［7］。附加惯性力是指飞艇作加速运动时所带动的周围空气产生的反作用，即附加惯性力，计算方法如下：

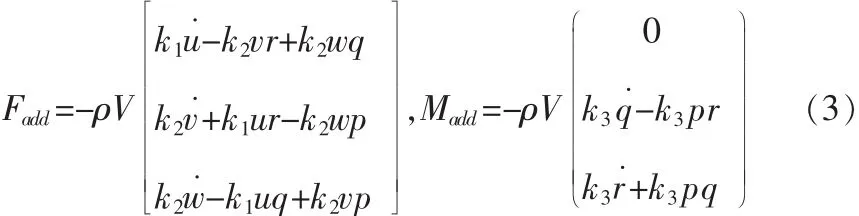
式中：k1、k2和k3是椭球惯性因子；V是飞艇的容积，ρ是空气密度。

平流层飞艇的螺旋桨布置有多种方式，文中选用安装在吊舱左右两侧加矢量推进方式，安放位置如图1所示。设螺旋桨的推力为FT，螺旋桨俯仰角为μ，Srt为作用点矩阵，则

1.3动力学模型

根据动量和动量矩定力给出的刚体六自由度动力学模型为：

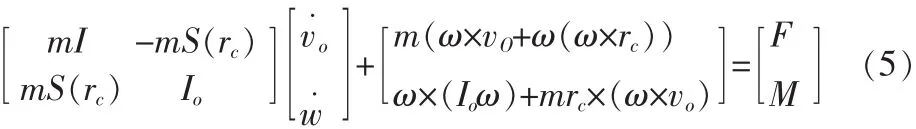
由于飞艇关于xz平面对称，故惯性积Ixy=Iyz=0，质心的坐标yc=0。

2　PID神经网络控制器设计

2.1PID神经元网络结构

PID神将元网络从结构上可以分为输入层、隐含层和输出层3层［8］。隐含层由比例元、积分元和微分元构成，分别对应着PID控制器中的比例控制、积分控制和微分控制。单控制量神经元网络的拓扑结构如图2所示。

图2　单控制量神经元网络拓扑结构Fig.2　Topological structure of single control variable neural network

2.2控制率设计

从前述的平流层飞艇动力学模型可以看出，飞艇的控制项来自舵面以及推力，控制量数量n=6。输入层中包含12个神经元，输出数据与输入数据相等。隐含层的计算公式如下：

式中：n为并联子网络的序号；j为子网络中隐含层神经元序号；ωij为各子网络输入层至隐含层的连接权重值。输出层有6个神经元，由隐含层输出结果进行加权后获得：

式中：usj（k）和ωjk分别为隐含层输出结果以及向输出层的连接权值。

2.3权值修正

PID神经元网络在控制的过程中根据控制量误差按照梯度修正法修正权值，使得控制量不断接近控制目标值，权值修正中的误差计算公式如下。

式中，n为输出节点个数；yh为预测输出；r为控制目标。

2.4网络权值的粒子群算法优化

一般的PID神经元网络由于采用的是梯度学习法实现对样本数据的学习，这种算法容易使学习过程进入局部最优解［9］。为了改善学习效果，引入粒子群优化算法实现对网络初始权值的优化。粒子群算法设置：种群规模为50，进化次数为40，采用自适应变异方法提高种群搜索能力。

3　模型仿真

根据前文建立的数学模型以及PID神经网络控制器，利用Matlab/Simulink进行模型仿真。算例飞艇采用文献［10］中的总体设计，设计参数如表1所示。

表1　平流层飞艇设计参数Tab.1　Design parameters of stratospheric airship

平流层飞艇姿态控制主要研究对于期望姿态的跟踪问题。主要参考指标为飞艇的3个姿态角［θ，ψ，φ］T，控制量由舵面和推力构成［FT，x，FT，z，δRUDT，δRUDB，δELVL，δELVR］T，控制量的取值范围如表2所示。

表2　控制量取值范围Tab.2　Value range of control variables

将姿态［θ，ψ，φ］T的期望值分别设置为［5°，10°，3°］T，得到的仿真结果如图3所示。相比较于传统的PID控制器，PID神经网络控制器不仅能够满足达到期望值的基本要求，而且速度更快，精度也更高，同时也避免了过度超调和震荡延时过大等不利影响。原因在于PID神经网络不仅具备传统PID的基本特点，还利用神经网络在线动态调整的能力，以其较强的灵活性和适应性弥补了传统PID的不足，使控制器的控制效果更为出色。

为了进一步提高PID神经网络的学习效率，加入了动量项用来对学习方法进行优化。带动量项的PID神经网络控制效果如图4所示，通过加入动量项进行修正以后的控制响应明显更快，和未加入前相比，控制响应速度提高了一倍左右。

4　结　论

本文在建立了平流层飞艇完整六自由度动力学模型的基础上，提出了PID神经网络控制器的设计方法。结果表明，和传统的PID控制器相比，PID神经网络结构的控制响应更快，精度更高。在引入动量项修正和粒子群算法优化的情况下能够进一步提升PID神经网络控制器的学习效率，且能够降低陷入局部最优解的概率。通过PID神经网络控制器能够完成平流层飞艇的姿态跟踪控制。

图3　PID神经网络控制器控制效果Fig.3　Results of PID neural network

图4　加入动量项修正的控制效果Fig.4　Results of PID neural network with momentum term

［1］Paiva Ely Carneiro de，Bueno Samuel Siqueira，Bergerman Marcel.A robust Pitch Attitude Controller for Aurora’s Semi-Autonomous Robotic Airship［C］//AIAA Lighter-Than-Air Systems Technology Conference.AIAA，1999：1-8.

［2］Acosta D M，Joshi S S.Adaptive Nonlinear Dynamic InversionControl of an Autonomous Airship for the Exploration of Titan［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.AIAA，2007：1-13.

［3］Hygounenc E，Soueres P.Automatic Airship Control Involving Backstepping Techniques［C］//IEEE International Conference on Systems，Man and Cybemetics.IEEE，2002：1-6.

［4］Trevino R，Frye M，Franz J A.Robust Receding Horizon ControlofATri-TurbofanAirship［C］//2007IEEE International Conference on Control and Automation.IEEE，2007：671-676.

［5］李智斌，吴雷，张景瑞，等.平流层飞艇动力学与控制研究进展［J］.力学进展，2012，2012（4）：482-493.

［6］苗景刚.飞艇动力学分析及运动控制［D］.北京：中国科学院研究生院，2008.

［7］刘丹，王晓亮，单雪雄.平流层飞艇的附加质量及其对飞艇运动的影响［J］.计算机仿真，2006，23（6）：52-56.

［8］孙东阳，易文俊.基于PID神经网络的滑翔增程制导炮弹解耦控制系统设计［J］.计算技术与自动化，2011，30（2）：21-25.

［9］肖军，章玮玮，郭晓鹏，等.基于模糊PID控制的飞艇压力调节系统设计［J］.辽宁工程技术大学学报（自然科学版），2010，29（5）：807-809.

［10］Lee S，Bang H.Three-dimensional ascent trajectory optimization for stratospheric airship platforms in the jet stream［J］. Journal of Guidance，Control and Dynamics，2007，30（5）：1341-1352.

Stratospheric airship attitude control based on PID neural Network

ZHANG Yi，LIU Long-bin
（School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

In view of stratospheric airship attitude control，this paper describes the flight control law design using PID neural network.First，a complete six-degree-of-freedom dynamic model of airship is addressed on the basis of flight characteristics. Based on the model，the structure and calculation method of PID neural network are proposed，and the initial weight values of network are optimized using particle swarm optimization.A simulation example is given to show applicability，rapid response speed and high calculation accuracy of the PID neural network control law which is suitable for the accurate control of the stratosphere airship attitude.

PID neural network；stratospheric airship；attitude control；particle swarm optimization

TN710

A

1674－6236（2016）03-0016-04

2015-03-24稿件编号：201503334

张 一（1988—），男，天津人，博士研究生。研究方向：飞行器总体设计。