基于直觉模糊C-均值聚类算法的图像分割

兰　蓉, 马姣婷

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)



基于直觉模糊C-均值聚类算法的图像分割

兰蓉, 马姣婷

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

基于直觉模糊集理论对模糊C-均值(Fuzzy C-Means，FCM)聚类算法进行改进。采用模糊补算子生成非隶属度，得出相对应的直觉模糊集犹豫度，用于更新模糊C-均值聚类算法中的模糊隶属度值。针对常用测试图像的仿真实验结果显示，在分割的视觉效果几乎一致的情况下，改进算法在迭代效率上相对于原FCM聚类算法有一定提高。

直觉模糊集；模糊C-均值；模糊补；犹豫度

图像分割是把人们感兴趣的图像根据灰度、纹理、形状、颜色等特定准则划分成若干个具有相同性质的类别的过程[1]，是由图像处理到图像分析的关键步骤。现今国内外广泛使用的图像分割方法有区域生长法、基于边缘检测的方法、模糊聚类法和阈值化法等[2]。

在基于聚类分析的众多图像分割算法中，基于模糊C-均值(Fuzzy C-Means，FCM)聚类的图像分割是应用最为广泛的算法之一。该算法原理简单，能自适应迭代获得最终的分割结果，是一种无监督的聚类方法，但与此同时，该方法也存在着许多缺陷。文[3]运用划分隶属度构造相对熵理论，提出相对熵FCM聚类分割算法，解决了无法获得复杂图像的细节信息问题；文[4]就FCM聚类对含噪图像分割时未充分考虑空间信息的问题，提出一种改进的FCM聚类算法；文[5]针对FCM运行速度远比硬C-均值(Hard C-Means，HCM)聚类慢的问题，采用奖励样本点的最大隶属度，同时降低其他隶属度的方式提出了抑制式FCM聚类算法；针对模糊集的单值隶属度不能充分描述不确定性信息的问题，Atanassov通过引入犹豫度概念的方式，提出了直觉模糊集合理论[6]。文[7]分析了抑制式FCM聚类算法的研究现状，并建议可以在相关算法中引入奖优罚劣的竞争学习思想。

本文将直觉模糊集合理论与竞争学习的思想相结合，提出一种改进的基于直觉模糊集的模糊C-均值(Intuitionistic Fuzzy Sets-Fuzzy C-Means，IFS-FCM)聚类算法。并且，对多幅实验图像进行分割测试，从分割效果和迭代次数两方面进行算法性能的评价。

1　相关理论

1.1直觉模糊集

模糊集[8]只考虑隶属度，直觉模糊集对模糊集进行了扩展，把犹豫度也考虑其中。

定义1[9-10]有限论域X={x1,x2,…,xn}上的直觉模糊集A定义为

A={(x,uA(x),vA(x)): x∈X}。

其中

uA: X→[0,1],vA: X→[0,1],

分别称为直觉模糊集A的隶属度函数与非隶属度函数，且满足

0≤uA(x)+vA(x)≤1 (x∈X)。

当uA(x)=1-vA(x)时，直觉模糊集退化为了模糊集。为了能更好地反映数据的不确定性和未知性，Atanassov在直觉模糊集概念的基础上引入了犹豫度πA(x)。元素x对直觉模糊集A的犹豫度可以表示为

πA(x)=1-uA(x)-vA(x)。

显然可以得到0≤πA(x)≤1。

在直觉模糊集的定义中引入犹豫度后，隶属度的取值范围以区间形式表示为

[uA(x),uA(x)+πA(x)]。

1.2FCM算法

FCM算法的目标函数可表述为带约束条件的极值问题，即

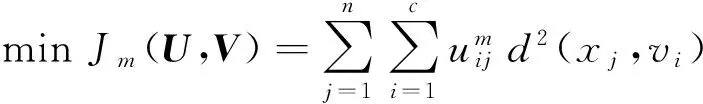
其中，m是隶属度的平滑参数，一般取2；uij表示样本xj相对于第i个聚类的隶属度值，满足

uij∈[0,1](1≤i≤c,1≤j≤n),

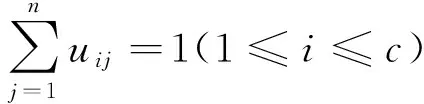
d(xj,vi)=‖xj-vi‖2。

(1)

式(1)表示样本点xj到聚类中心vi的欧氏距离。

该带约束条件的极值问题可通过拉格朗日乘子法求解，相应的迭代算法描述如下。

步骤1初始化。设定聚类类别数C和迭代停止的条件ξ。并初始化隶属度矩阵U(0)，令k=0。

步骤2计算聚类中心

V(k)=[vi(k)]，

其中

步骤3计算隶属度矩阵

U(k+1)=[uij(k+1)],

其中

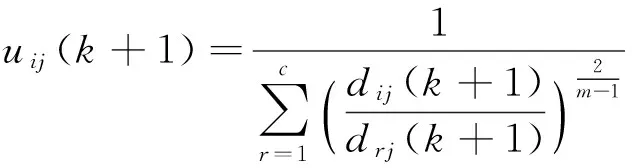
步骤4如果|U(k)-U(k+1)|<ξ,就停止循环迭代，否则令k=k+1回到步骤2继续迭代。

2　基于直觉模糊集改进的FCM算法

2.1直觉模糊集的生成

从模糊集转变到直觉模糊集的过程中，直觉模糊补运算起着至关重要的作用。对任意x∈[0,1]，若φ[0,1]→[0,1]满足φ(x)≤1-x，则称φ为直觉模糊补[11]。

为了和模糊指数m相区别,在此将带参数的广义模糊补，即m-模糊补[12]，记为m0-模糊补。对任意隶属度函数u(x)∈[0,1]，m0∈[0,1],实函数

即为m0-模糊补。

在直觉模糊集中，用m0-模糊补生成非隶属度函数，则犹豫度可以表示为

对于直觉模糊集来说,隶属度函数u(x)和非隶属度函数v(x)总是满足

0≤u(x)+v(x)≤1。

2.2新的直觉模糊C-均值算法

基于直觉模糊集改进的FCM聚类算法相比原FCM聚类算法在两方面进行了改进：一方面通过引入犹豫度来修正隶属度函数，另一方面为提高算法的效率，对隶属度值进行奖优罚劣，从而在原算法中引入了竞争机制。具体操作步骤即在步骤4之前插入一个对uij(k)的修改过程。

步骤3*对每个样本xj，记

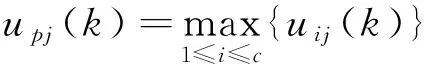
其中

这里的πij(k)是以m0-模糊补生成的犹豫度，用来修正隶属度函数，并根据参数m0来控制算法的抑制程度。

上述算法就是基于直觉模糊集改进的FCM算法。当参数m0=0.5时，犹豫度变为0，该算法就退化为FCM算法，故FCM聚类算法是所提出算法的特殊情形。基于直觉模糊集改进的FCM算法是原FCM算法在直觉模糊集概念基础上进行的推广。

3　实验结果与分析

改进算法包括如下参数：聚类的类别数C,迭代停止的条件ξ和非隶属度控制参数m0。其中，聚类类别数C根据具体的灰度图像要分割的类别数进行确定，迭代停止的条件取ξ=10-5，因此需要确定的是影响分割效率与分割效果的非隶属度控制参数m0。在本文中取分割效果普遍较好时的经验值，即m0=0.7。为验证改进的基于直觉模糊集的FCM算法的有效性，选取了五幅灰度图像ct_slice.jpg，mri.tif，shot.tif，rice.png和cameraman.tif分别进行了仿真实验，用来比较分割效果。针对图1所示的5幅图像，分别利用FCM和IFS-FCM进行图像分割，效果如图2所示。

图1　实验所用图像

(a) FCM

(a) IFS-FCM

两种算法针对5幅图像的平均迭代次数和运行时间如表1所示。

实验结果显示，通过犹豫度来改变隶属度函数，基于直觉模糊集的改进FCM算法可以得到跟FCM聚类算法几乎一致的视觉分割效果，但IFS-FCM算法的效率有所提高，迭代次数和运行时间也有显著减少。

表1　两种算法的平均迭代次数和运行时间对比

4　结语

图像分割是当今国内外学者研究的重要内容，FCM算法具有描述简洁、容易实现和分割效果好等特点，在图像分割中发挥着十分重要的作用。然而，它也存在鲁棒性差、迭代时间长等不足，在一定程度上限制了FCM的进一步应用。通过引入奖优罚劣的竞争机制，并结合直觉模糊集提出了基于直觉模糊集改进的FCM聚类算法，利用犹豫度的大小来确定隶属度的修正值。实验表明，该算法能有效地提高聚类算法的效率，并得到较理想的图像分割效果，故具有一定的应用价值。另外，鉴于m0是影响算法效果与效率的重要参数，如何自适应地选取最优的参数值成为值得进一步研究的问题。

[1]徐胜军,韩九强,刘光辉.基于马尔可夫随机场的图像分割方法综述[J/OL].计算机应用研究,2013,30(9):2576-2582[2015-10-03].http://www.arocmag.com/article/01-2013-09-004.html.

[2]王芳梅,范虹,WANGY.利用改进CV模型连续水平集算法的核磁共振乳腺图像分割[J/OL].西安交通大学报,2014,48(2):38-43[2015-10-03].http://www.jdxb.cn/oa/DArticle.aspx?type=view&id=201402007.DOI:10.7652/xjtuxb201402007.

[3]田小平,张忠宝,吴成茂.相对熵模糊C均值聚类分割算法[J/OL].西安邮电大学学报,2015,20(5):38-42[2015-10-10].http://www.cnki.net/kcms/doi/10.13682/j.issn.2095-6533.2015.05.007.html.

[4]李琳,范九伦,赵凤.模糊C-均值聚类图像分割算法的一种改进[J/OL].西安邮电大学学报,2014,19(5):56-60[2015-10-11].http://www.cnki.net/kcms/doi/10.13682/j.issn.2095-6533.2014.05.011.html.

[5]FANJL,ZHENWZ,XIEWX.Suppressedfuzzyc-meansclusteringalgorithm[J/OL].PatternRecognitionLetters,2003,24(9/10):1607-1612[2015-10-15].http://www.sciencedirect.com/science/article/pii/S0167865502004014.DOI:10.1016/S0167-8655(02)00401-4.

[6]ATANASSOVKT.Intuitionisticfuzzysets[J/OL].FuzzysetsandSystems,1986,20(1):87-96[2015-10-15].http://www.sciencedirect.com/science/article/pii/S0165011486800343.DOI: 10.1016/S0165-0114(86)80034-3.

[7]范九伦.抑制式模糊C-均值聚类研究综述[J/OL].西安邮电大学学报,2014,19(3):1-5[2015-10-17].http://www.cnki.net/kcms/doi/10.13682/j.issn.2095-6533.2014.03.001.html.

[8]CHAIRAT,RAYA.Fuzzymeasuresforcolorimageretrieval[J/OL].FuzzySetsandSystems,2005,150(3):545-560[2015-10-18].http://www.sciencedirect.com/science/article/pii/S0165011404004038.DOI: 10.1016/j.fss.2004.09.003.

[9]HUNGWL,YANGMS.SimilaritymeasuresofintuitionisticfuzzysetsbasedonHausdorffdistance[J/OL].PatternRecognitionLetters,2004,25(14):1603-1611[2015-10-20].http://www.sciencedirect.com/science/article/pii/S0167865504001424.DOI: 10.1016/j.patrec.2004.06.006.

[10]HUNGWL,YANGMS.SimilaritymeasuresofintuitionisticfuzzysetsbasedonLpmetric[J/OL].InternationalJournalofApproximateReasoning,2007,46(1):120-136[2015-10-20].http://www.sciencedirect.com/science/article/pii/S0888613X06001228.DOI: 10.1016/j.ijar.2006.10.002.

[11]BUSTINCEH,KACPRZYKJ,MOHEDANOV.Intuitionisticfuzzygeneratorsapplicationtointuitionisticfuzzycomplementation[J/OL].Fuzzysetsandsystems,2000,114(3):485-504[2015-10-21].http://www.sciencedirect.com/science/article/pii/S0165011498002796.DOI: 10.1016/S0165-0114(98)00279-6.

[12] 支晓斌,范九伦.一种广义模糊补运算和相应的广义模糊熵[J/OL].模糊系统与数学,2008,22(1):96-102[2015-10-22].http://www.cnki.com.cn/Article/CJFDTOTAL-MUTE200801019.htm.

[责任编辑:瑞金]

Image segmentation based on intuitionstic fuzzy C-means clustering algorithm

LAN Rong,MA Jiaoting

(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

The fuzzy C-means(FCM) clustering algorithm is improved based on the theory of intuitionistic fuzzy set. The non membership degree is generated by using the fuzzy complementary operator, and thus, the corresponding hesitation degree can be figured out to update the membership function of fuzzy C-means clustering algorithm. A simulation experiment on common testing images is done, and the results show that, as the visual effects of the segmentation are almost identical, the improved algorithm can get some increasement on the iterative efficiency in relation to the original FCM clustering algorithm.

intuitionstic fuzzy sets, fuzzy C-means(FCM), fuzzy complementary, hesitation degree

10.13682/j.issn.2095-6533.2016.04.010

2015-11-18

国家自然科学基金资助项目(61571361)；陕西省科技计划资助项目(2014KJXX-72)；陕西省教育厅科学研究计划资助项目(15JK1658)

兰蓉(1977-)，女，博士，副教授，从事模式识别和决策分析研究。E-mail:ronglanlogic@163.com

马姣婷(1990-)，女，硕士研究生，研究方向为信息安全。E-mail:majiaoting888@163.com

TP391

A

2095-6533(2016)04-0053-04