基于Harr小波的CS-MRI典型重构算法的性能分析
2016-09-13任筱倩汤敏南通大学电子信息学院江苏南通226019
任筱倩,汤敏(南通大学电子信息学院,江苏 南通,226019)
基于Harr小波的CS-MRI典型重构算法的性能分析
任筱倩,汤敏
(南通大学电子信息学院,江苏 南通,226019)
目的 压缩感知理论(Compressed Sensing,CS)与磁共振成像(Magnetic Resonance Imaging,MRI)相结合,缩短MRI图像数据的扫描时间,提高成像质量。方法 以Harr小波进行稀疏表达,分别利用基追踪(Basis Pursuit,BP)算法、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法和分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit,StOMP)算法实现CS-MRI的二维重构。结果 在采样率较低(10%-50%)时,以峰值信噪比(Peak Signal to Noise Ratio,PSNR)、平均结构相似度(Mean Structure Similarity,MSSIM)、相对误差(Relative L2 Norm Error,RLNE)和传输边缘信息(Transferred Edge Information,TEI)四个指标来定性、定量地评价和比较上述三种算法的重构质量,BP算法性能最佳。结论 BP算法能精确重构原始图像,与完整采样图像相比,图像质量并无明显下降,同时大大减少MRI采集时间,具有重要的理论意义和临床应用价值。
压缩感知;重构算法;小波变换;Harr小波;MRI图像
0 引言
传统的信号获取和处理过程分为信号采样、变换、压缩和重构这四个方面,其中信号获取过程必须满足香农采样定理,即信号的采样频率不得小于模拟信号频谱中最高频率的2倍,然后在信号压缩过程中,进行某一特定变换后少数绝对值较大的数据进行压缩,丢弃系数为零或接近零的数据。显然,这种以香农采样定理为标准的高速采样,然后再对采集获得的信号进行压缩的过程,浪费了大量的采样资源,同时在数据传输和存储中也导致巨大的资源浪费。针对上述传统信号获取和处理过程中存在的问题,Donoho、Candes、Romberg和Tao等人在大量理论研究的基础上正式提出压缩感知理论(Compressed Sensing,CS),可以通过对有限个采样数据的重构,实现近似精确或者精确地恢复原始信号或图像[1-3]。
磁共振成像(Magnetic Resonance Imaging,MRI),是根据磁共振现象从人体获取电磁信号,并且由该信号重建出人体信息的一种断层成像技术,已成为常用的无创医学成像技术之一,在临床医学诊断中具有重要地位。但是,由于MRI扫描仪器所采集到的信号是经过全局傅里叶变换后得到的频域图像,从而导致MRI成像时间过长,对于老人、小孩等无法长时间保持静止的人群而言检测效果不佳,对肺、胃、肠道等运动性器官而言,也可能导致图像模糊。针对上述MRI的不足之处,Lustig提出CS-MRI成像理论,即从MRI的K空间数据的子集中准确重构出原始信号或图像[4]。CS-MRI改变了医学信息的获取方式,将采样速度提高到原来的几十甚至几百倍,使得扫描时间大为减少,重构图像具有较高的空间分辨率,在临床应用中备受关注。
本文研究基于Harr小波的CS-MRI图像的压缩感知二维重构,对典型算法进行性能分析和比较。算法流程如下:首先采用Harr小波变换实现MRI图像的稀疏表达,然后分别利用基追踪(Basis Pursuit,BP)算法、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法和分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit,StOMP)算法实现CS-MRI图像的二维重构,并以峰值信噪比(Peak Signal to Noise Ratio,PSNR)、平均结构相似度(Mean Structure Similarity,MSSIM)、相对误差(Relative L2 Norm Error,RLNE)和传输边缘信息(Transferred Edge Information,TEI)这四项指标来定性、定量地评价和比较上述三种重构算法的性能。
1 压缩感知理论框架
压缩感知理论的主要内容是指:在某一变换域内具有稀疏表示的信号,可以以远低于奈奎斯特采样定理标准的方式来采集数据,通过与变换基非相干的随机投影采样,运用合适的优化算法高概率精确重构原始信号。该理论框架主要包含稀疏表示、测量矩阵和重构算法三个方面,详见图1[1-3,5]。
由图1可见,原始信号在某些变换域中具有稀疏性,是压缩感知精确重构原始信号的先验条件;测量矩阵的选取与设计,直接影响随机测量值是否保留了足够的原始信号信息,能够精确重构原始信号重构算法则是压缩感知理论的核心,直接影响信号重构质量和重构速度。目前压缩感知理论的重构算法主要分成贪婪算法、凸优化算法、组合算法和统计优化算法这四类。
(1)贪婪算法——基本思想是以当前情况为基础作出最优选择,通过迭代方法逐步更新重构信号的支撑集,进而求解出最小l0范数问题的解。贪婪算法主要包括:子空间追踪算法、匹配追踪算法、正交匹配追踪算法、分段正交匹配追踪算法、正则化正交匹配追踪算法等。根据选择的支撑集元素是否采用回验机制,还可以将这几种重构算法划分为两类:非回验算法,即对于已选入支撑集的元素不会被再次选入或者删除;回验算法,对已选中的某些元素可将其重新加入支撑集或不将其删除[6]。
(2)凸优化算法——基本思想是将非凸问题转化成凸优化问题来求最优解,即将求解l0范数问题转化为求解最小l1范数的线性问题,逐渐逼近原始信号以得到精确的重构结果。常用的凸优化算法包括:基追踪算法、内点法、迭代阈值算法、加权迭代算法、梯度投影稀疏重建算法等。
(3)组合算法——首先对原始信号进行高度采样,再对采样结果进行群测试以获得信号支撑。常用的组合算法包括:链追踪算法、稀疏傅里叶描述算法、HHSP追踪(Heavy Hitters On Steroids Pursuit,HHSP)算法等。
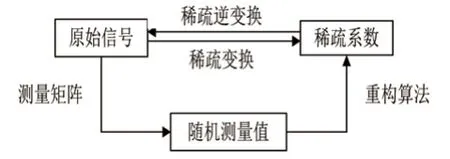
图1 压缩感知基本理论框架Fig.1 Theory Framework of Compressed Sensing
(4)统计优化算法——利用典型信号的训练集对信号的主要成分或者独立成分进行分析,找出信号的最优线性投影集合。目前的统计优化方法主要分为基于训练集合学习的统计优化算法和基于贝叶斯统计理论的稀疏重构算法。
2 典型重构算法
2.1BP算法
Donoho等学者提出:在一定条件下,求解最小l0范数问题与求解最小l1范数问题是等价的。BP算法是对由测量向量组成的不同组合,采用线性优化模型进行处理,以求得最优解,获得较佳的重构结果,但其计算复杂度较高。
BP算法的求解过程中,原始信观测矩阵,基矩阵φ已知,求解s 等同于求解x ,其中s, x∈RN,y∈RM,M<N。算法求解,满足φxˆ=y ,其中。在含噪情况下,求解,其中n 为噪声,σ≥0为噪声强度,且,其约束条件可改为,满足,对其进一步求解就可以重构出原始信号。其中参数σ表示算法允许误差的范围,其值为0时可认为是一般的无噪BP算法。
2.2OMP算法
Gilbert等人提出正交匹配追踪算法的基本思想是:在信号稀疏度为的条件下,通过贪婪迭代算法选择重构矩阵中的列,使得当前矩阵余量与每次迭代过程中选择的列最大程度相关,从而去掉矩阵中的相关部分,然后对矩阵中的余量再次进行迭代直至迭代次数满足残差条件为止[7]。这种强制停止迭代过程的方法使得OMP算法需要较多的线性测量值来保证精确重构。OMP算法的具体步骤如下[7-8]:
输入:采样向量s ,传感矩阵φ,稀疏度K;
输出:x的K稀疏逼近xˆ;
初始化:索引集Λ0=φ,残值r0=s,t=1;
循环执行Step1~Step5:
Step 1:寻找残值r 和传感矩阵的列ψj积中最大元素的索引λ;
Step 2:更新索引集Λ0,记录经由传感矩阵φ进行重构后的原子集合;

Step 3:进行最小二乘法;

Step 4:更新残值,t=t+1;

Step 5:如Step 4中t>K,则迭代停止;否则继续执行Step 1。
2.3StOMP算法
Donoho等学者在正交匹配追踪算法的基础上,采用分阶段的思想,提出了分段正交匹配追踪算法,首先从最初的原子集合中筛选出满足阈值条件且与迭代余量相匹配的原子,然后对现有的支撑集和原子进行更新,最后利用最小二乘法求解得出近似精度,并且对迭代余量的更新完毕[9-10]。StOMP算法在分段处理阶段中,首先构建一个残差矢量序列r1,r2,……,然后建立一个逼近序列X0,X1,……Xs,Is标记Xs中非零元素的坐标值,初始解X0=0,Is为空,具体迭代步骤如下:
Step 1:初始化,设定最大迭代步长、最大迭代误差e、s=1;
Step 2:将小波变换后获得的稀疏矩阵记为y ,进行随机测量;

Step 3:对Θ进行规范化处理,K为Θs信号长度;

Step 4:对Θ进行阈值处理;

Step 5:最新合并两次变换所得的坐标索引,并对Is集合进行一致化处理;

Step 6:求解线性方程组min(||x||s 1)s.t.y=φXS ,计算公式如下;

Step 7:计算残差rs;

Step 8:稀疏解的精度判定,如rS<e,则X0=Xs;否则s=s+1,返回Step 3。
3 实验结果与分析
3.1评价指标
医学图像的质量要求较高,需要算法能够有效重构图像,本文采用峰值信噪比PSNR、平均结构相似度MSSIM、相对误差RLNE、传输边缘信息TEI这四个指标共同定性、定量地评价上述算法的重构性能。
PSNR计算公式如下:

其中,f( x, y)和f′(x, y)分别为完整采样图像和重构图像,M×N为图像空间分辨率。PSNR值越大,表示重构图像与完整采样图像越接近,重构效果越好,重构精度越高。
结构相似度(Structural Similarity,SSIM),通过对完整采样图像和重构图像进行对比,来判断两者之间的相似度,更符合人眼对图像的视觉判断,计算公式如下[11-12]:
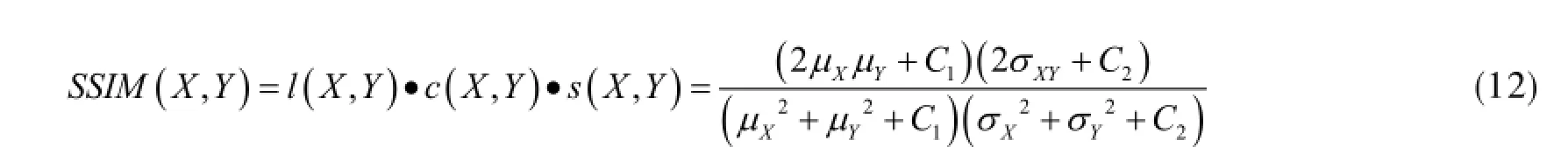
其中,µx和σx是原始图像的均值和标准差,µy和σy是重构图像的均值和标准差,σxy是两幅图像的联合方差,c1和c2是为了防止分母接近零时产生不稳定现象而添加的固定常数。
平均结构相似度MSSIM是在SSIM基础上发展而来的,首先利用大小相同的窗口对完整采样图像X 和重构图像Y 进行分块,确保各分块之间不重叠,然后计算各块的结构相似度,计算公式如下:

RLNE用来衡量两幅图像的结构不相符度,其值越小,表示重构图像与完整采样图像之间的误差越小,两者更接近,计算公式如下[13-14]:

TEI用于衡量重构图像与完整采样图像在保持图像边缘信息方面的差异,计算公式如下[15]:

其中,Qgxy和xy分别表示边缘保持和方向保持的数据;G其值越大表示重构图像边缘信息保持越好。
3.2实验结果分析
本实验在处理器为Intel Core i3-2330M CPU@ 2.20GHz的机器上,采用MATLAB R2010b编程实现。首先以世界公认的Shepp Logan模型作为测试图像,比较BP、OMP、StOMP算法在10%-50%欠采样率下的重构效果,性能指标参见表1。同时,为从人眼视觉系统直观感受重构图像质量,图2-图4给出10%采样率下的重构图像、误差图像和局部放大图像。

表1 Shepp Logan模型在不同欠采样率下的重构性能指标Table 1 Performance Comparison of BP, OMP, StOMP Algorithms for Shepp Logan Phantom
由表1和图2—图4(第20页),可以得出以下结论:(1)随着欠采样率的增大,BP算法和OMP算法重构图像的PSNR逐步增大,TEI和MSSIM越来越大并接近1,RLNE越来越小,这显然与压缩感知理论完全符合;(2)StOMP重构算法重构出的图像呈现PSNR、TEI和MSSIM越来越小,而RLNE却越来越大的趋势,这是因为StOMP算法在迭代过程中不一定能够找到信号的最佳表示方法,使得重构精度大大降低,且稀疏度选取也不是很合适;(3)在相同欠采样率条件下,OMP算法重构图像的PSNR小于BP算法,RLNE指标略高于BP算法,这说明在相同的欠采样率下,BP算法对于Shepp Logan模型的重构图像质量明显优于OMP算法;(4)在相同采样率情况下,BP重构算法运行时间最长,但图像重构质量最佳,重构误差最小,重构图像与原图更接近。

图2 采样率10%时Shepp Logan 模型的重构图像Fig.2 CS-MRI Recovery Results of Shepp Logan Phantom at 10% Sampling Ratio

图3 采样率10%时Shepp Logan模型的重构误差图像Fig.3 Recovery Error Images of Shepp Logan Phantom at 10% Sampling Ratio

图4 采样率10%时Shepp Logan模型的局部放大图像Fig.4 Local Magnification Images of Shepp Logan Phantom at 10% Sampling Ratio
由于Shepp Logan图像是严格数学解析的,因此图像重构误差均由算法产生,上述实验充分说明BP、OMP算法均能很好地实现欠采样条件下的压缩感知二维重构。下面选取图5所示的真实MRI图像,进一步验证上述算法的有效性和实用性。表2-表4分别是图5所示三幅MRI图像在不同欠采样率下图像重构的性能指标。
图5 真实MRI图像Fig.5 Truly MRI Images
从表2-表4可以看出,对于真实MRI图像,在10%-50%欠采样率下,BP算法总能获得最佳的性能指标。以MRI-Brain.jpg图像为例,图6-图8是其在25%欠采样率下的重构图像、误差图像和局部放大图像。

表2 MRI.jpg图像不同采样率下的重构性能指标Table 2 Performance Comparison of BP, OMP, StOMP Algorithms for MRI.jpg
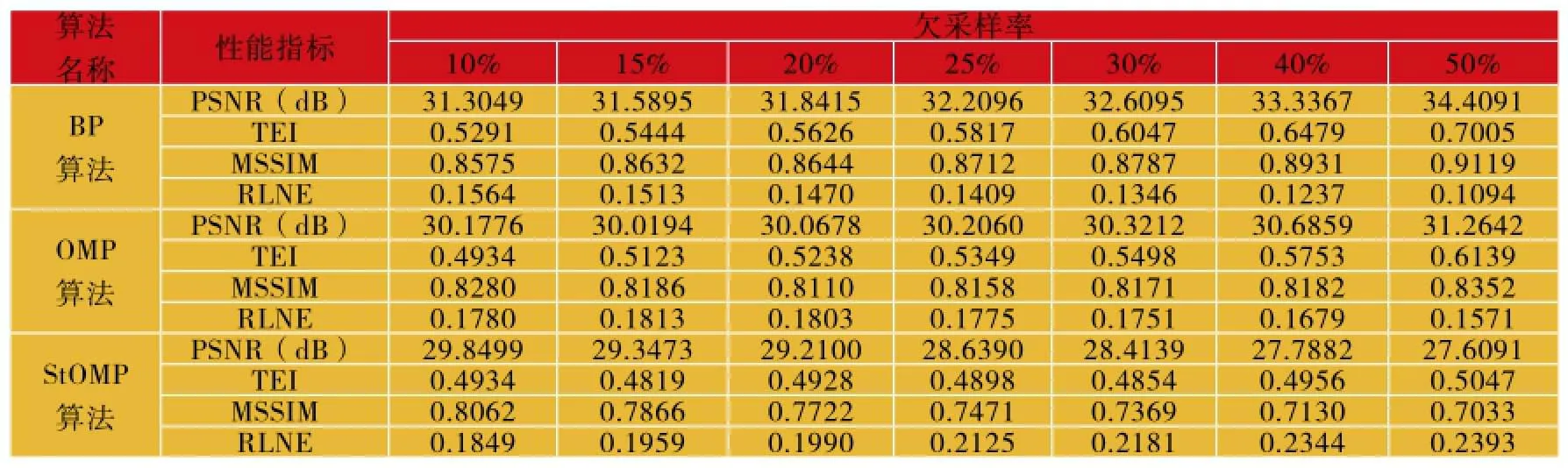
表3 Heart.png图像不同采样率下的重构性能指标Table 3 Performance Comparison of BP, OMP, StOMP Algorithms for Heart.png
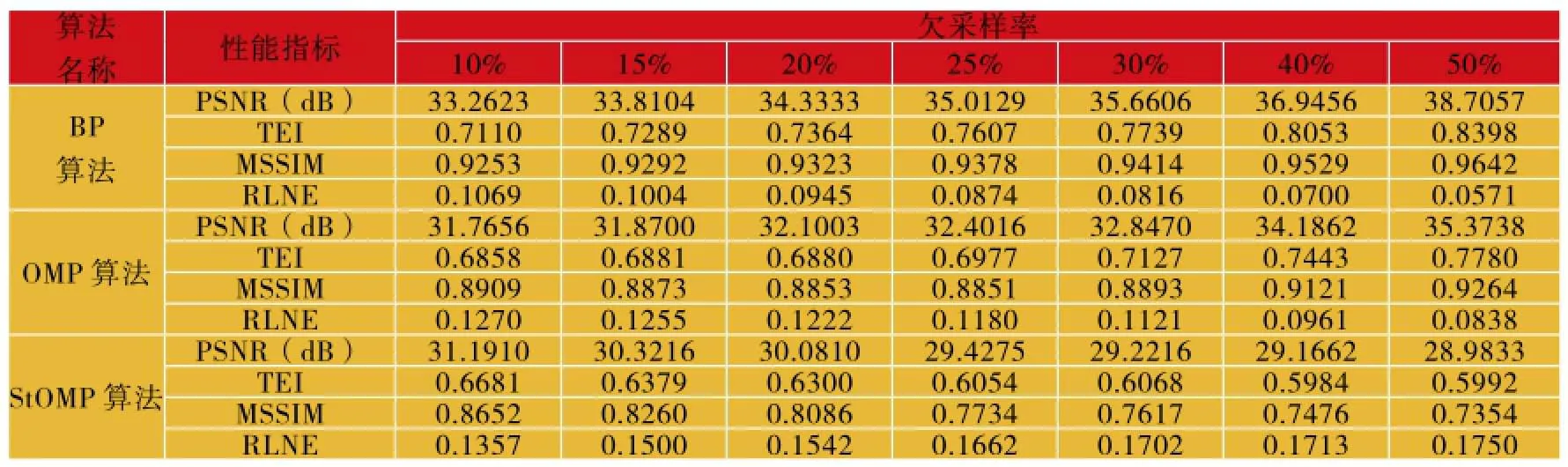
表4 MRI-Brain.jpg图像不同采样率下的重构性能指标Table 4 Performance Comparison of BP, OMP, StOMP Algorithms for MRI-Brain.jpg

图6 采样率25%时的MRI-Brain.jpg图像重构结果Fig.6 CS-MRI Recovery Results of MRI-Brain.jpg at 25% Sampling Ratio
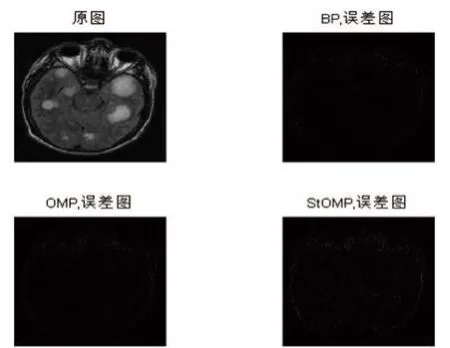
图7 采样率25%时的MRI-Brain.jpg图像重构误差图像Fig.7 Recovery Error Images of MRI-Brain.jpg at 25% Sampling Ratio

图8 采样率25%的MRI-Brain.jpg局部放大图像Fig.8 Local Magnification Images of MRI-Brain.jpg at 25% Sampling Ratio
由表2-表4和图6-图8可知,对于真实MRI图像而言,(1)随着欠采样率增大,BP算法和OMP算法重构出的图像PSNR、TEI和MSSIM越来越大,RLNE越来越小,同时,BP算法的各项性能指标均最优;(2)欠采样率≥30%以后,BP算法重构图像与完整采样图像之间的误差基本<10%,可应用于临床真实MRI图像的压缩感知重构。
4 讨论与结论
伴随信息技术的蓬勃发展,生活中所需处理的信息量越来越大,使得信息在采集、存储及传输等方面所面临的压力也越来越大,传统信号的采集与压缩过程在实际运用过程具有许多不适应的地方,压缩感知理论则较好地解决了目前面临的采样速度慢、存储及传输量巨大的问题。
本文在简要阐述压缩感知理论框架和重构算法原理的基础上,利用BP、OMP和StOMP算法对严格解析的Shepp Logan模型和真实MRI图像进行了不同欠采样率的压缩感知二维重构,结论如下:(1)在相同欠采样率的情况下,BP算法的重构结果最佳,虽运算时间最长,但仍可满足实时性的要求;StOMP算法重构结果最差,不适用于临床应用;(2)在采样率较低的情况下,利用压缩感知理论可以近似精确地重构出原始MRI图像,解决了传统采样时间长和采集后数据大量浪费的问题,缩短采样时间,提高图像质量,这对于MRI临床应用具有重要的理论价值和实用前景。
今后的研究方向包括:(1)在图形处理器GPU上实现算法的硬件加速,从而在保证BP算法重构误差最小,重构精度最高的同时,尽量缩短其运行时间;(2)将本文算法应用于更多不同部位、不同疾病的CS-MRI图像重构中,检验算法的普遍适用性。
[1] David Donoho. Compressed Sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[2] Emmanuel J. Candes, Justin K Romberg, Terence Tao. Stable Signal Recovery from Incomplete and Inaccurate Measurements [J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.
[3] Emmanuel J. Candes, Justin K Romberg, Terence Tao. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Fourier Information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[4] Michael Lustig, David Donoho, John Pauly. Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging [J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195.
[5] Yonina Eldar, Gitta Kutyniok. Compressed Sensing: Theory and Applications [M]. Cambridge University Press, 2012
[6] 王超. 基于压缩感知的贪婪迭代重构算法[J]. 数据采集与处理,2012,27(S2):298-303.
[7] Tropp J, Gilbert A. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
[8] 杨真真,杨震,孙林慧. 信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理,2013,29(4):486-496.
[9] Maleki A, Donoho D L. Optimally Tuned Iterative Reconstruction Algorithms for Compressed Sensing [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 330-341.
[10] 解成俊,张铁山. 基于压缩感知理论的图像重构算法研究[J]. 计算机应用与软件,2012,29(4): 49-52.
[11] Zhou Wang, Alan C. Bovik, Hamid R. Sheikh, Eero P. Simoncelli. Image Quality Assessment: From Error Visibility to Structural Similarity [J]. IEEE Transaction on Image Processing, 2004, 13(4): 600-612.
[12] Xiao Chen, Michael Salerno, Yang Yang, Frederick H. Epstein. Motion-Compensated Compressed Sensing for Dynamic Contrast-Enhanced MRI Using Regional Spatiotemporal Sparsity and Region Tracking: Block LOw-rank Sparsity with Motion-guidance (BLOSM)[J]. Magnetic Resonance in Medicine, 2014, 72(4): 1028-1038.
[13] Xiaobo Qu, Yingkun Hou, Fan Lam, Di Guo, Jianhui Zhong, Zhong Chen. Magnetic Resonance Image Reconstruction From Undersampled Measurements Using a Patch-Based Nonlocal Operator [J]. Medical Image Analysis, 2014, 18(6): 843-856.
[14] Yunsong Liu, Zhifang Zhan, Jian-Feng Cai, Di Guo, Zhong Chen, Xiaobo Qu. A Simple and Fast Iterative Soft-thresholding Algorithm for Tight Frames in Compressed Sensing Magnetic Resonance Imaging [J]. arXiv preprint arXiv:1504.07786, 2015.
[15] C.S. Xydeas, V. Petrovic. Objective Image Fusion Performance Measure [J]. Electronics Letters, 2000, 36(4): 308-309.
Performance Analysis of CS-MRI Recovery Algorithms Based on Harr Wavelet
REN Xiao-Qian, TANG Min
(School of Electronics and Information Engineering, Nantong University, Nantong 226007, China)
Objective The CS (Compressed Sensing) theory is introduced into MRI (magnetic resonance imaging) to solve the shortcomings of the long acquisition time of MRI, and to change the way of medical imaging techniques. Methods Three typical CS-MRI recovery algorithms, including basis pursuit (BP), orthogonal matching pursuit (OMP) and stagewise orthogonal matching pursuit (StOMP) are analyzed and compared based on the Harr wavelet. Results Four performance indices-peak signal to noise ratio (PSNR), mean structural similarity (MSSIM), relative l2 norm error (RLNE) and transferred edge information (TEI) are applied to evaluate the recovery image’s quality under different sampling ratios. It is clear that the BP algorithm achieves the best performance. Conclusion The original reference images can be accurately recovered based on BP algorithm under the low sampling ratios (10%-50%), which has important theoretical significance and clinical application foreground in MRI technique.
Compressed sensing; Reconstruction algorithm; Wavelet transform; Harr wavelet; MRI images
国家自然科学基金资助项目(61401239);江苏省自然科学基金资助项目(BK20130393);江苏高校品牌专业建设工程资助项目(PPZY2015B135)
汤敏,女,汉族,江苏南通人,副教授,硕士生导师,从事医学图像处理与分析等相关研究。
