三辊非对称滚弯成形的数值仿真及试验验证

王　艳　胡捷飞　许光辉　李曙生　熊　巍

1.上海理工大学，上海，200093　　2.镇江市锻压机床厂，镇江，2120003.泰州职业技术学院，泰州，225300



三辊非对称滚弯成形的数值仿真及试验验证

王艳1,2胡捷飞1许光辉2李曙生3熊巍1

1.上海理工大学，上海，2000932.镇江市锻压机床厂，镇江，2120003.泰州职业技术学院，泰州，225300

基于有限元法对三辊非对称滚弯成形工艺进行了研究，对比分析了三辊非对称滚弯成形和三辊对称滚弯成形过程中，变形区应力场、板材上表面的塑形应变场及卷制力的变化规律。仿真结果表明：侧辊位移进给量相同的工况下，三辊非对称滚弯成形的卷制力大于三辊对称滚弯成形的卷制力；三辊非对称滚弯变形区的纵向应力和径向应力均大于三辊对称滚弯成形的纵向应力和径向应力；三辊非对称滚弯成形板材压弯段的成形质量高于三辊对称滚弯成形的成形质量。最后，经三辊非对称滚弯试验验证，有限元模型的成形误差为6.8%，有较高的精度。

三辊非对称滚弯；应力场；卷制力；成形精度

0　引言

滚弯成形工艺是一种无切削、高效率、高质量的生产工艺,相比传统的板材加工工艺, 它具有高效、省材、低成本、精度高等优点，因此，滚弯成形工艺在造船、石油化工、锅炉、压力容器等行业已经得到广泛的应用[1]。三辊滚弯成形工艺是工业应用最为广泛的一种滚弯成形工艺，根据加工时三个轧辊间的相对位置分布，它又可分为对称滚弯成形和非对称滚弯成形两种。与三辊对称滚弯成形工艺相比，三辊非对称滚弯成形工艺一次上料即可完成筒体卷制加工，并能有效减少成形筒体的剩余直边，可进一步提高生产效率。

滚弯成形工艺涉及轧辊与板材间的摩擦、接触以及板材的回弹，是一个复杂的成形过程[2]。板材滚弯成形工艺是设计卷板装备、制定弯卷工艺、提高卷板精度和实现弯卷自动控制的理论基础，具有重要研究价值和现实意义[3]。目前研究者对于三辊非对称滚弯成形工艺的研究主要是分析工艺参数对三辊非对称滚弯成形的影响和三辊非对称滚弯工艺模型的建立等方面。Tran等[4]分析了侧辊位移进给量、板材尺寸等工艺参数对三辊非对称滚弯成形的影响，并研究了滚弯过程中板材表面塑性应变的演变规律。Feng等[5]针对板材的三辊非对称滚弯工艺建立了侧辊位移进给量与板材最终成形半径的滚弯工艺模型，并结合试验对工艺模型进行了验证。Zhang等[6]在考虑板材外形尺寸、工作辊直径、板材与工作辊摩擦等因素的基础上，对中厚板弹塑性三辊非对称压弯工艺过程进行了工艺模型的建立与试验验证。但是研究者对于三辊非对称滚弯成形过程中，板材变形区内部应力应变状态、板材的回弹、塑性变形、卷制力等方面却少有研究，也未能进一步结合三辊对称滚弯成形工艺对三辊非对称滚弯成形工艺的特点进行对比分析。

本文针对上述问题，首先应用有限元软件ABAQUS，分别建立三辊对称滚弯成形和三辊非对称滚弯成形的二维动态有限元模型。其次通过对比分析对称滚弯和非对称滚弯成形过程中，变形区应力的分布特点、卷制力的变化规律以及板材上表面塑性应变场的分布规律，对三辊非对称滚弯成形工艺的机理及特点进行研究。最后结合三辊非对称滚弯成形试验,对有限元模型的成形精度进行验证。

1　三辊非对称滚弯工艺模型

三辊非对称滚弯时，通过调整侧辊相对于上辊的位置来控制板材滚弯成形后的成形半径。在上辊和下辊对变形区板材的夹持作用下，三辊非对称滚弯变形区近似关于上辊与下辊辊心连线对称，并假设板材在变形区内成形曲率一致。基于上述假设，根据侧辊相对位置与成形后板材的几何关系，即可推导出侧辊位移进给量与板材成形半径的数值关系。如图1所示，非对称滚弯时，侧辊沿倾角方向的位移进给量为d，板材最终成形半径为Rf，此时侧辊辊心相对坐标为(x0,y0)，距上辊辊心距离为a。图1中，A表示侧辊倾斜角与上下辊辊心连线的交点；ψ为侧辊倾角。

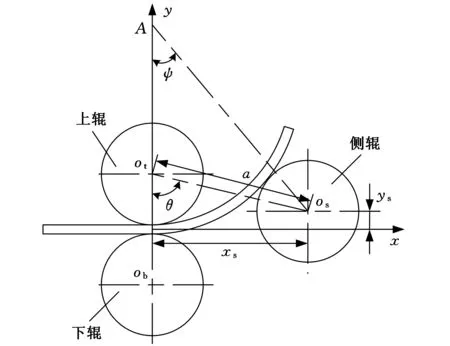
图1　侧辊与板材成形半径的几何关系示意图

假设非对称滚弯成形时，塑性变形后的板材与直边部分始终相切，则根据图1所示的几何关系，推导出侧辊辊心相对坐标(xs,ys)与板材回弹前成形半径R的关系式[7]：

(1)

式中，Rb为下辊半径；θ为侧辊辊心与上辊辊心连线与垂线的夹角；T为板厚。

三辊非对称滚弯成形时，侧辊辊心初始位置相对坐标(x0,y0)及侧辊辊心相对位置坐标(xs,ys)满足下式：

(2)

侧辊的位移进给量d为

(3)

板材回弹后的成形半径才是最终成形半径Rf。回弹与板材的弹性模量、屈服极限、板材厚度、板材自重、板与轧辊间的摩擦等因素有关，因此，难以建立高精度的回弹模型。工程上一般采用的板材回弹模型[8]，经变换后为

(4)

式中，K0、K1分别为相对强化系数和形状系数(矩形截面取值为1.5)；E为弹性模量；σs为屈服极限。

联立式(1)～式(4)即可确定侧辊位移进给量d与非对称滚弯后板材成形半径Rf间的数值关系。

2　有限元模型的建立

2.1几何模型

本文采用ABAQUS/Explicit模块的显式中心差分算法对三辊非对称滚弯成形和三辊对称滚弯成形过程进行动态仿真。分别建立三辊非对称滚弯成形和三辊对称滚弯成形的二维有限元模型，如图2所示。轧辊在滚弯过程中的弹性变形量很小，将其设定为刚体。板材厚度为30 mm，选用可变形的平面应力应变单元CPS4R，并沿厚度方向将板材网格划分为6层。有限元模型中轧辊直径参数见表1、表2。滚弯加工时上辊为主动辊，转速为0.3 rad/s，下辊及侧辊为从动辊。三辊非对称滚弯成形加工时，侧辊沿30°倾角倾斜向上进给；三辊对称滚弯成形时，下辊也沿30°倾角倾斜向上进给，如图2所示。

表1　三辊非对称有限元模型轧辊直径

表2　三辊对称有限元模型轧辊直径

2.2接触定义

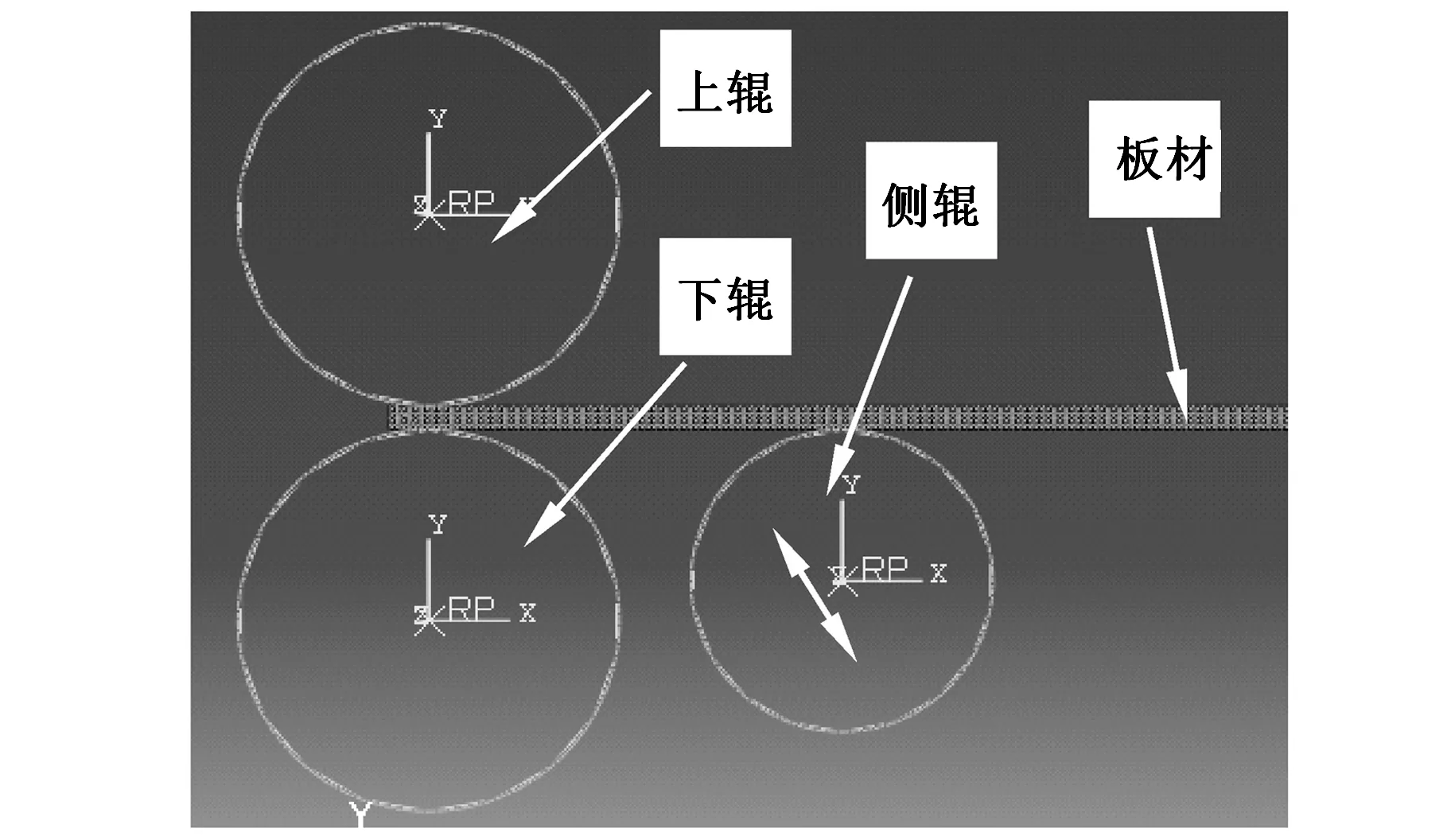
(a)非对称滚弯有限元模型

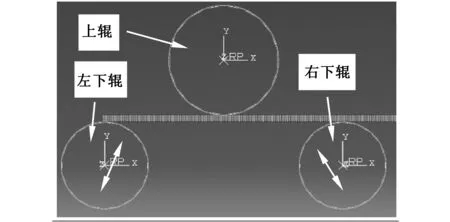
(b)对称滚弯有限元模型图2　滚弯成形有限元模型

滚弯成形涉及复杂的接触过程，对于板材与轧辊间的接触，采用surface to surface接触，并将刚体轧辊表面定义为主面，板材表面定义为从面。采用罚函数摩擦模型求解轧辊与板材间的接触，其中三辊非对称滚弯模型中，为减小侧辊对板材的摩擦阻力，保证板材的顺利送料[9]，将上下辊与板材间的摩擦因数设为0.15[10]，将侧辊与板材间的摩擦因数设为0.1；在对称滚弯模型中，将上辊与板材间的摩擦因数分别设为0.15，而下辊与板材间的摩擦因数设为0.1。

2.3材料模型

仿真试验选用的钢板材料为Q235B钢板，材料属性[6]如下：屈服应力σs为235MPa；弹性模量E为210GPa；泊松比μ为0.3；密度ρ为7800kg/m3；强化系数K为1900。假设板材材料为各向同性，且不考虑板材自重对滚弯成形的影响。

滚弯成形过程中板材发生弹塑性变形，必须在ABAQUS中设置板材材料的本构关系。因双线性强化模型能够较好地拟合材料的真实本构关系[11]，本文采用双线性强化模型定义板材的本构关系，以模拟板材在滚弯成形过程中发生的塑性变形。本构方程为

(5)

式中，σ为应力；ε为应变；εe为弹性应变极限。

3　仿真结果分析

3.1三辊非对称滚弯成形工艺过程

三辊非对称滚弯仿真模拟过程如图3所示，与三辊对称滚弯成形过程相同[11]，可将三辊非对称滚弯成形过程分为三个阶段：①压弯阶段。此时侧辊沿倾角斜向进给，对板材端部进行压弯。②过渡滚弯阶段。上辊转动对板材端部进行滚弯。③稳态滚弯阶段。上辊继续转动对板材进行连续的滚弯。过渡滚弯阶段是压弯阶段到稳态滚弯阶段的一个过渡阶段，历时较短，因此，可将滚弯成形后的板材沿长度方向主要分为压弯段和稳态滚弯段，而稳态滚弯段筒体的成形半径即为筒体的整体半径。

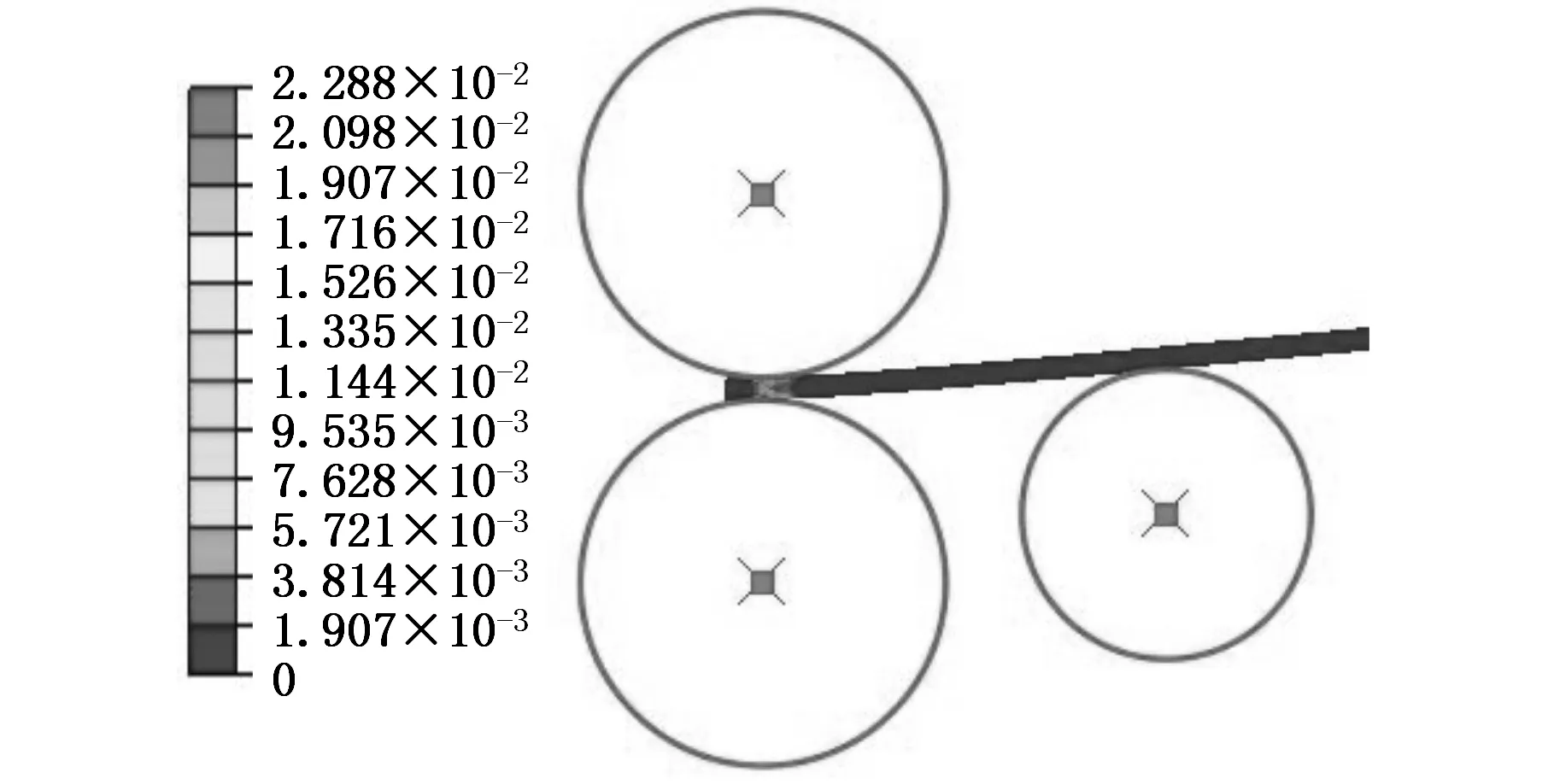
(a)压弯阶段

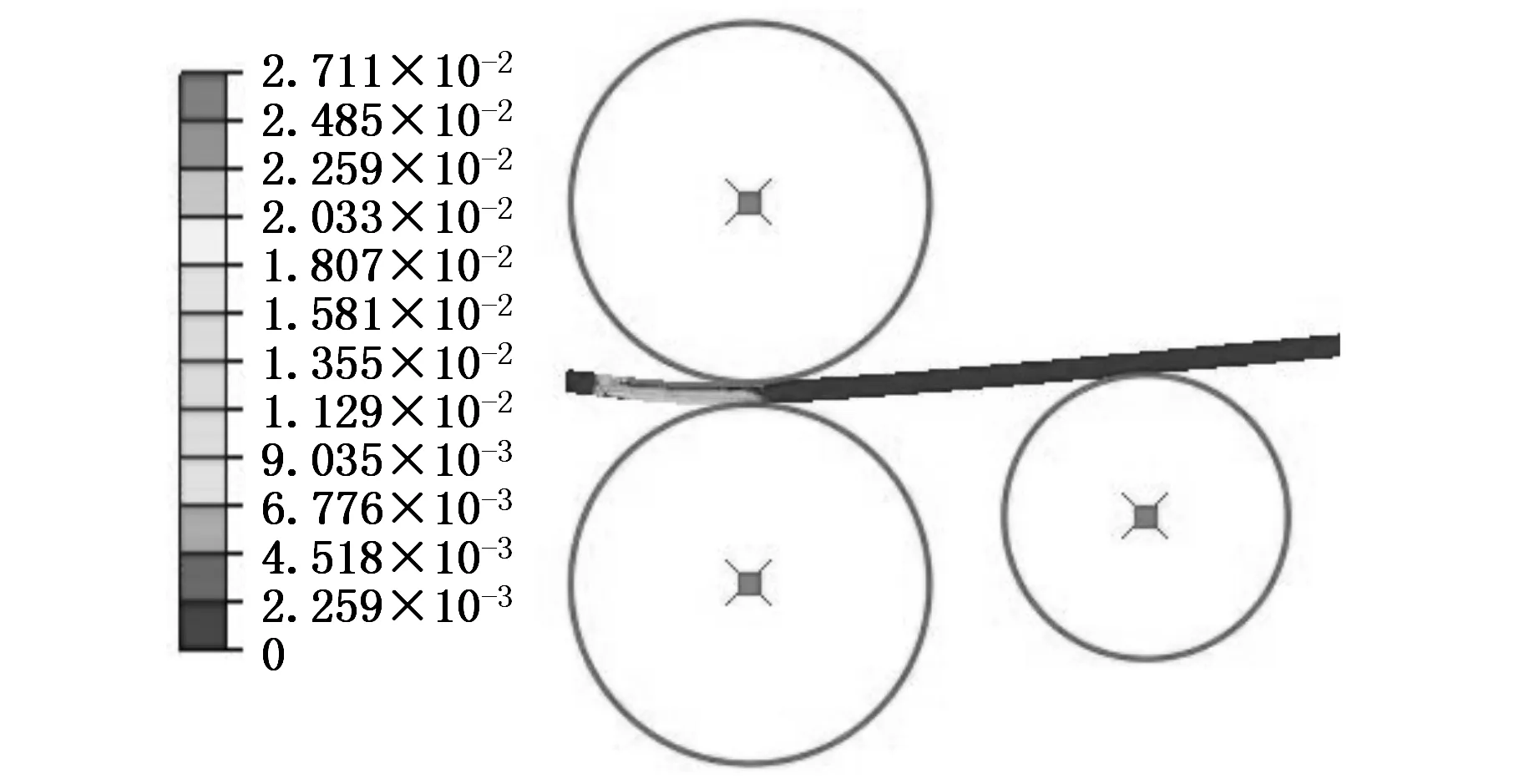
(b)过渡滚弯阶段

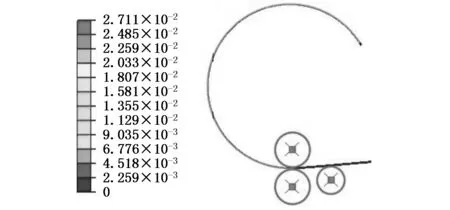
(c)稳态滚弯阶段图3　非对称滚弯模拟过程

3.2变形区应力场演变分析

图4所示为滚弯成形过程中变形区厚度方向截面应力分布曲线。由图4a，在侧辊位移进给量相同的工况下，三辊非对称滚弯成形时，变形区内纵向应力和径向应力均大于三辊对称滚弯成形的纵向应力和径向应力。对于三辊对称滚弯成形，其变形区内截面纵向应力远大于径向应力，因此，变形区内径向应力对三辊对称滚弯成形的影响可忽略。但是由于上下辊的夹持作用，三辊非对称滚弯变形区内径向应力要明显大于对称滚弯成形的径向应力，因此，必须考虑径向应力对非对称滚弯成形的影响。板材的回弹是一个弹性应变能释放的过程，滚弯成形后板材的残余应力会随着弹性应变能释放量的增加而减小。图4b所示为回弹后板材厚度方向截面应力分布曲线。由图4b，三辊非对称滚弯成形后，板材截面应力要小于对称滚弯成形的应力，即非对称滚弯成形后板材的残余应力比对称滚弯成形的残余应力小。在滚弯变形区内，板材受力状态为上压下拉，这种受力状态会增大板材回弹量[12]。非对称滚弯成形时，变形区截面纵向应力大于对称滚弯成形的纵向应力，因此，其回弹量也会相应增大，而随着板材回弹量的增大，残余应力也会随之减小。

(a)变形区截面应力分布曲线

(b)回弹后残余应力分布曲线图4　截面厚度方向上应力演变

3.3板材周向应变场分布分析

滚弯成形后，板材上表面的塑性应变场分布体现了滚弯成形质量。图5所示为滚弯成形后板材上表面的塑性应变场分布情况。由图5可知，三辊对称滚弯成形与三辊非对称滚弯成形后，在压弯段，板材均存在较大的残余塑性应变。对称滚弯成形后，压弯段与稳态滚弯段的塑性应变差为0.013，非对称滚弯成形的两段间的塑性应变差为0.003。板材纯弯曲时上表面应变与成形半径的关系如下：

εr=1-r/rm

(6)

式中，εr为板材上表面应变；r为上表面成形半径；rm为板材中心层成形半径。

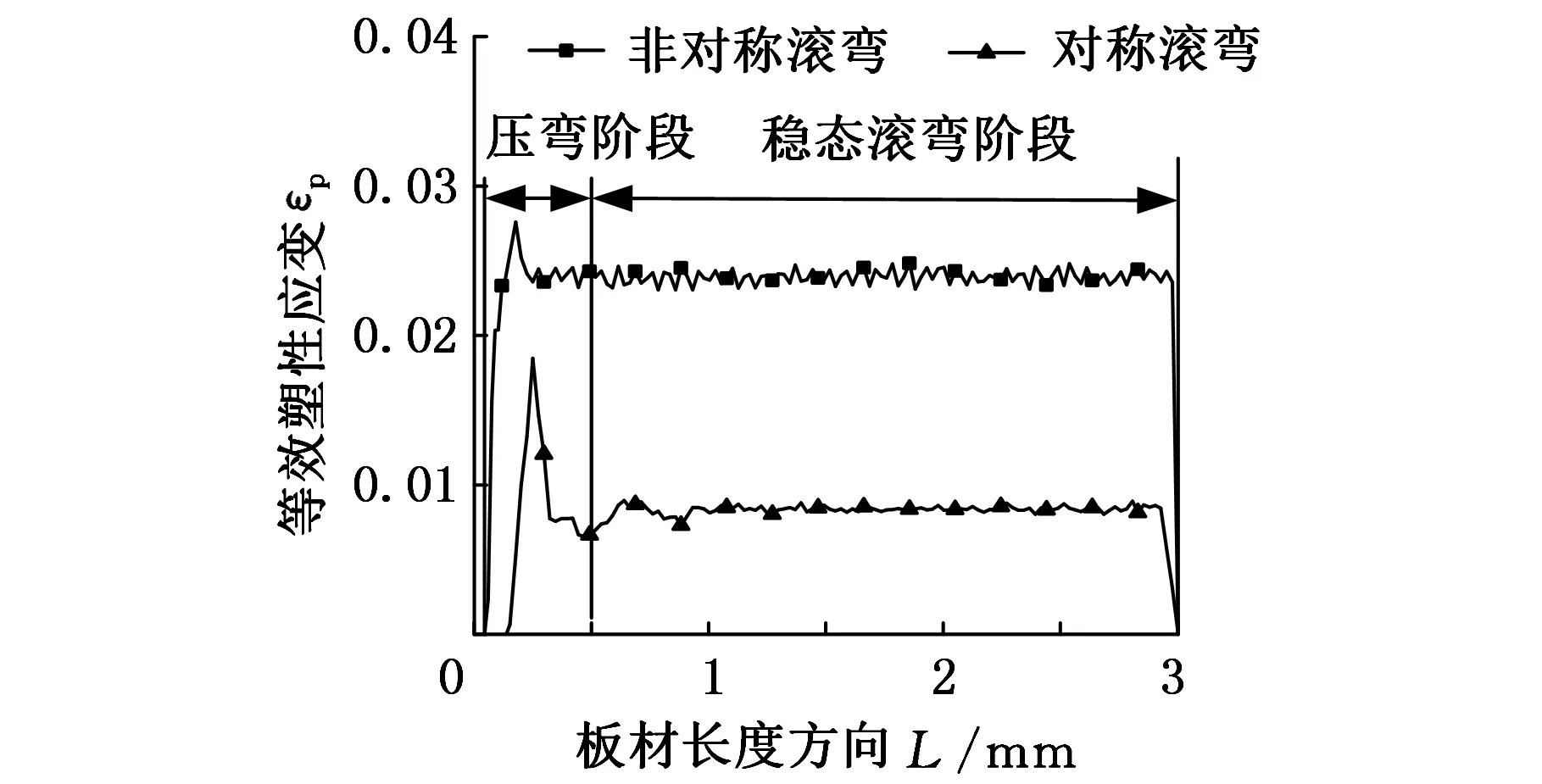
图5　板材上表面塑性应变场分布

由式(6)可知，压弯段与稳态滚弯段间的塑性应变差必然导致压弯段与稳态滚弯段的成形半径不一致，而两段成形半径的一致性是滚弯成形质量的重要体现。因此，三辊非对称滚弯成形后，压弯段与稳态滚弯段间成形半径的一致性要高于对称滚弯成形两段成形半径的一致性，即三辊非对称滚弯成形后板材压弯段成形质量较高。随着滚弯过程由压弯阶段过渡至稳态滚弯阶段，板材上表面的塑性应变波动也逐渐趋于稳定。在稳态滚弯阶段，与三辊非对称滚弯成形相比，对称滚弯成形后板材上表面的塑性应变分布波动较小，分布更加均匀，说明对称滚弯成形后板材稳态滚弯段的成形均匀度较高。经计算，在侧辊位移进给量为50 mm的工况下，稳态滚弯时，三辊非对称滚弯成形与对称滚弯成形，上辊与板材间的接触弧长分别为35 mm和20 mm。与板材轧制过程相似，滚弯成形过程中，接触弧长的增大会增大接触力，加剧轧辊的弹性变形，降低成形质量。而较小的接触弧长有益于提高成形的精度，并减小卷制力。因此，在侧辊位移进给量为50 mm的工况下，三辊非对称滚弯成形会增大滚弯变形区板材与轧辊间的接触面积，增大卷制力并加剧板材上表面的塑形应变波动，进而会降低滚弯成形质量。

3.4滚弯卷制力变化分析

滚弯成形过程中，侧辊与板材的接触力即为滚弯成形的卷制力。侧辊位移进给量为50 mm时，滚弯加工过程中卷制力随时间的变化曲线如图6所示。由图6，在压弯阶段，三辊非对称滚弯与对三辊对称滚弯的卷制力相近，并在压弯阶段结束时达到峰值142.5 kN。但随着滚弯过程由压弯阶段过渡至稳态滚弯阶段后，非对称滚弯与对称滚弯的卷制力均有所减小。在稳态滚弯阶段，三辊非对称滚弯成形所需的卷制力约为134.3 kN，而对称滚弯成形的卷制力约为118.2 kN。在三辊对称滚弯成形的压弯阶段，变形区近似关于上下辊辊心连线对称，但随着滚弯成形过程由压弯阶段向稳态滚弯阶段过渡，滚弯变形区也发生了转移[6]。而三辊非对称滚弯成形过程中，上辊和下辊对板材的夹持，使得非对称滚弯变形区的转移量小于三辊对称滚弯成形的转移量，因此，三辊非对称滚弯由压弯向稳态滚弯阶段过渡后，其卷制力的变化幅度会小于对称滚弯成形时卷制力的变化幅度。

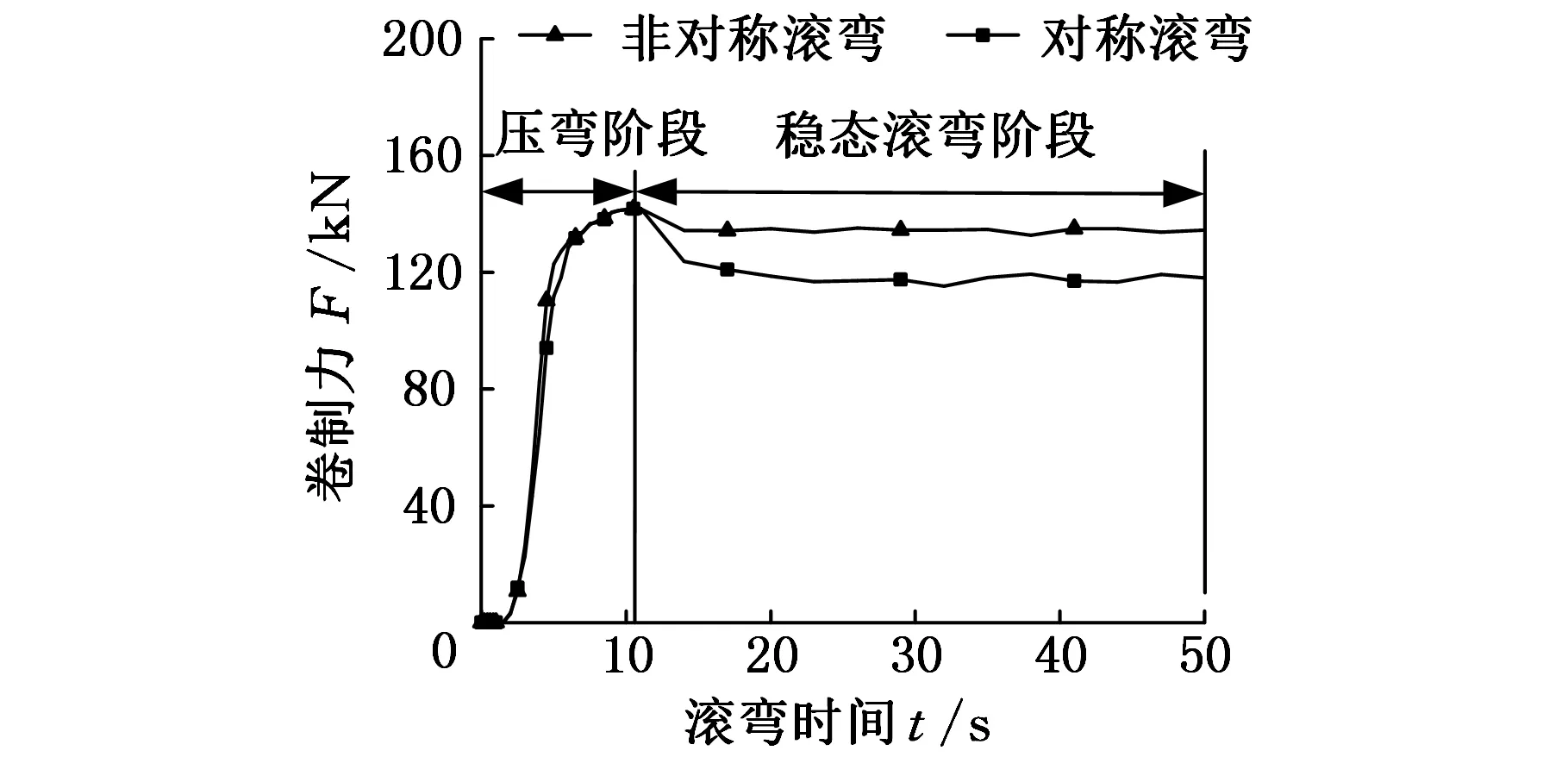
图6　滚弯成形卷制力变化曲线

图7所示为稳态滚弯阶段的卷制力随侧辊位移进给量的变化曲线。由图7,在侧辊位移进给量相同的工况下，稳态滚弯阶段，三辊非对称滚弯成形的卷制力要大于三辊对称滚弯成形的卷制力，且随侧辊位移进给量的增大，三辊非对称滚弯成形与三辊对称滚弯成形的卷制力的差值也逐渐增大。在侧辊位移进给量从30 mm逐渐增加至70 mm的过程中，三辊非对称滚弯成形与三辊对称滚弯成形的卷制力的差值也逐渐从13.1 kN增加至27.2 kN。

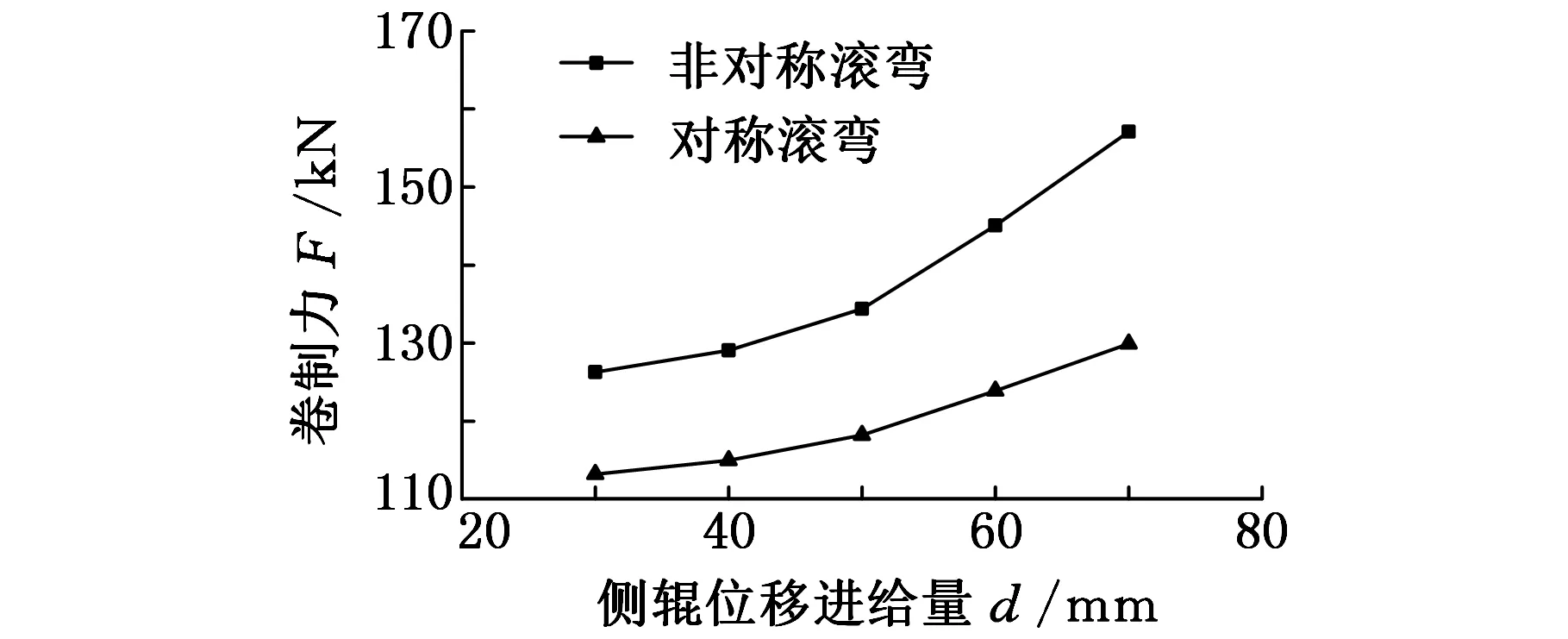
图7　不同侧辊位移进给量时卷制力变化曲线

4　试验验证

筒件的成形半径是滚弯变形区应力、应变及卷制力对滚弯成形的影响的直接体现，也是衡量滚弯成形质量的重要标准。本文通过三辊非对称试验，分析有限元数值仿真后筒件的成形半径精度，即可判断出有限元模型的准确性和可靠性。采用W1130×2500型三辊非对称卷板机，对尺寸为30 mm×1500 mm×7500 mm的Q235B钢板进行三辊非对称滚弯加工试验。驱动右辊沿侧辊倾角方向倾斜向上进给50 mm对板材进行三辊非对称滚弯加工。图8为三辊非对称卷板机滚弯加工后的筒件与有限元数值仿真后筒件的对比图。

(a)试验滚弯加工后筒件

(b)仿真试验滚弯加工后筒件图8　滚弯试验与仿真结果对比

将滚弯成形后的筒件沿周向分为五段，采用数字半径测量仪，对各段筒件的中截面内径值进行测量。同时也将仿真成形后的筒件沿周向分为五段，并应用MATLAB数值拟合对各段板材成形半径进行测量。将试验实测成形半径值与仿真计算成形半径值列于表3。由表3可知，经三辊非对称滚弯成形后的筒件平均半径为1197.5 mm，在相同的加工工况下，有限元仿真得到的筒件平均半径为1115.1 mm，有限元模型成形半径误差为6.8%。整体上分析，有限元模型成形半径误差不超过7.0%，有较高的精度，验证了有限元模型的准确性和可靠性。

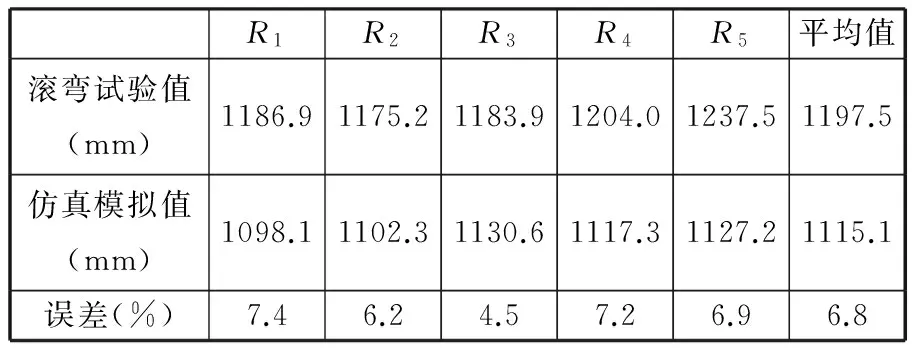
表3　滚弯试验值、仿真模拟值对比

误差产生的原因主要是有限元模型采用了二维建模，假设板材材料为各向同性，忽略板材自重及轧辊弹性变形对滚弯成形的影响。并且有限元模型采用了双线性强化模型，相对于材料的真实本构模型存在一定误差。同时有限元模型难以真实模拟出滚弯成形过程中板材的回弹，也会对有限元模型的精度产生影响，但其整体误差不超过7.0%，有着较高的精度和可靠性，可满足工程应用要求。

5　结论

(1)在侧辊位移进给量相同的工况下，稳态滚弯阶段，三辊非对称滚弯成形变形区内，板材厚度方向截面的纵向应力和径向应力均大于三辊对称滚弯成形的纵向应力和径向应力。

(2)在侧辊位移进给量相同的工况下，稳态滚弯阶段，三辊非对称滚弯成形的卷制力大于三辊对称滚弯成形的卷制力，且随侧辊位移进给量的增大，三辊非对称滚弯成形与三辊对称滚弯成形的卷制力的差值也逐渐增大。

(3)三辊非对称滚弯成形后，板材压弯段与稳态滚弯段的等效塑性应变差值小于三辊对称滚弯成形的等效塑性应变差值，因而三辊非对称滚弯成形后板材压弯段成形质量较高。

(4)三辊非对滚弯试验结果表明，有限元模型的成形半径误差为6.8%，有着较高的精度和可靠性。

[1]刑伟荣. 卷板机的现状与发展[J].锻压装备与制造技术, 2010, 45(2): 10-16.

Xing Rongwei. Status and Development of the Bending Machine for Plate[J]. China Metal Forming Equipment & Manufacturing Technology, 2010, 45(2): 10-16.

[2]杨建国, 方洪渊, 万鑫, 等. 大尺寸板材滚弯过程应力场特点分析[J].塑性工程学报, 2008, 16(5):684-687.

Yang Jianguo, Fang Hongyuan, Wan Xin, et al. Character of Stress in Large Dimensional PlateduringThree-roll Bending[J]. Journal of Plasticity Engineering, 2008, 16(5):684-687.

[3]仉志强, 宋建丽, 付建华, 等. 板材弯卷成形工艺的研究现状[J].塑性工程学报, 2014, 21(1): 1-6.

Zhang Zhiqiang, Song Jianli, Fu Jianhua, et al. Research Status of Plate Bending and Roll-bending Process[J]. Journal of Plasticity Engineering, 2014, 21(1): 1-6.

[4]Tran Q H, Champliaud H, Feng Zhengkun. Ana-lysis of the Asymmetrical Roll Bending Process through Dynamic FE Simulations and Experimental Study[J].The International Journal of Advanced Manufacturing Technology, 2014, 75(5/8):1233-1244.

[5]Feng Zhengkun, Champliaud H. Modeling and Simulation of Asymmetrical Three-roll Bending Process[J]. Simulation Modeling Practice and Theory, 2011, 19(9): 1913-1917.

[6]Zhang Zhiqiang, Song Jianli, Fu Jianhua, et al. A Refined Model of Three-roller Elastoplastic Asymmetrical Pre-bending of Plate[J]. Journal of Iron and Steel Research, International, 2014, 21(3):328-334.

[7]全建辉, 崔凤奎, 杨建玺, 等.基于ANSYS/LS-DYNA的花键冷滚轧成形数值模拟[J].中国机械工程, 2008, 19(4):419-421.

Quan Jianhui, Cui Fengkui, Yang Jianxi, et al. Numerical Simulation of Involute Spline Shaft’s Cold-rolling Forming Based on ANSYS/LS-DYNA[J]. China Mechanical Engineering, 2008, 19(4):419-421.

[8]李森, 陈富林, 李斌, 等. 四辊卷板机弯卷过程中侧辊位移计算[J].锻压技术, 2011, 36(6):76-79.

Li Sen, Chen Fulin, Li Bin, et al. Calculation of Side Roller Displacement for Four-roll Bending Plate Process[J]. Forging & Stamping Technology, 2011, 36(6):76-79.

[9]龚靖平, 黎向锋, 左敦稳, 等.小直径开缝衬套双轴柔性滚弯成形的三维有限元分析[J].中国机械工程, 2015, 26(8):1117-1123.

Gong Jingping, Li Xiangfeng, Zuo Dunwen, et al.Three-dimensional FEA of Manufacturing Process of Small-diameter Split Sleeve by Two-axle Bending[J]. China Mechanical Engineering, 2015, 26(8):1117-1123.

[10]俞汉清, 陈金德. 金属塑性成形原理[M].北京:机械工业出版社, 1999.

[11]仉志强, 宋建丽, 付建华,等.中厚板三辊弹塑性压弯建模与试验[J].塑性工程学报, 2013, 20(5):102-106.

Zhang Zhiqiang, Song Jianli, Fu Jianhua, et al. Modelling and Testing for Three-roller Elastic-plastic Bending of Moderate-thick Plate[J]. Journal of Plasticity Engineering, 2013, 20(5):102-106.

[12]刘章光, 高海涛, 刘继伟, 等.TA15钛合金板材冷折弯成形的有限元模拟及实验研究[J].热加工工艺, 2014, 43(13):129-133.

Liu Zhangguang, Gao Haitao, Liu Jiwei, et al. Finite Element Simulation and Experimental Study on Cold Bending Forming of TA15 Titanium Alloy Sheet[J].Hot Working Technology, 2014, 43(13):129-133.

(编辑陈勇)

Numerical Simulation and Experimental Verification of Asymmetrical Three-roll Bending Process

Wang Yan1,2Hu Jiefei1Xu Guanghui2Li Shusheng3Xiong Wei1

1.University of Shanghai for Science and Technology, Shanghai, 200093 2.Forging Machine Tool Plant of Zhenjiang, Zhenjiang, Jiangsu,212000 3.Taizhou Polytechnic College, Taizhou, Jiangsu,225300

The stress field of deformation zone, the stain field of upper plate surface and the changes of roll bending forces were analyzed during the asymmetrical and symmetrical roll bending process by the finite element(FE) simulation method. The simulation results show that the bending force during the asymmetrical roll bending process is larger than that during symmetrical roll bending under the same feed distance of the side roll. Compared to the asymmetrical roll bending process, the longitudinal and radial stress in deformation zone in the symmetrical roll bending process are smaller. The forming accuracy of the asymmetrical roll bending process of the pre-bending section is higher than that of symmetrical roll bending process.The experimental verification of a typical plates for the asymmetrical roll bending process was conducted, the result show that the forming error of FEA model is 6.8%.The FEA model has a higher forming accuracy.

asymmetrical three-roll bending; stress field; bending force; forming accuracy

2015-10-26

2015江苏省重点研发计划资助项目(BE2015139)

TG306

10.3969/j.issn.1004-132X.2016.15.018

王艳，女，1969年生。上海理工大学机械工程学院教授、博士。主要研究方向为磨削加工与特种加工。胡捷飞，男，1990年生。上海理工大学机械工程学院硕士研究生。许光辉，男，1975年生。镇江市锻压机床厂工程师。李曙生，男，1972年生。泰州职业技术学院机电技术学院教授、博士。熊巍，男，1982年生。上海理工大学材料科学与工程学院讲师。