基于FPGA的进位保留Barrett模乘法器设计与实现

车文洁，高献伟

（北京电子科技学院 北京 100070）

基于FPGA的进位保留Barrett模乘法器设计与实现

车文洁，高献伟

（北京电子科技学院 北京 100070）

在有限域上的模算术运算中，乘法运算最基础且最耗时，因此为提高公钥密码体质的运算速度，设计出运算速度快、消耗时间少的模乘法器非常关键。该文设计出进位保留Barrett模乘法器，乘法部分利用进位保留乘法器，求模运算部分利用Barrett约减运算，用硬件描述语言进行FPGA设计与实现，避免了除法运算。对于192位的操作数，完成Barrett模乘需要约186个时钟周期，计算速率可以达到269.17 Mb/s。

Barrett模约减；Barrett模乘法器；FPGA；硬件描述语言

作为目前最受欢迎的公钥密码算法，ECC具有传输带宽少、处理速度快、存储空间占用小、灵活性高及安全性好等优点［1］，公钥密码算法均以模算术运算为基本运算，其操作数通常是大整数，运算量较大、耗时多，模算术运算的效率决定了公钥密码系统的运行效率，设计出高效模乘法器一直是公钥研究领域的关注焦点，本文设计出的模乘法器运算速度高，耗时较少，在公钥密码系统有较高的实用性。

1 进位保留并行乘法器

利用进位保留并行乘法器原理，得出电路图如图1所示。

该结构图由1×1乘法器的n×m阵列组成，其耗时等于n·T（1，1）加上m位输出加法器的延时。关键路径如上图阴影部分所示。其计算时间等于

2 Barrett模约减运算

即使m不属于非特殊形式的模数，xmodm的计算仍属于模运算，属于模乘运算中较耗时的部分。由于域乘法的速度是ECC算法的运算速度快慢的关键，因此选择模很重要。

图1 进位保留并行乘法器Fig.1 Carry-save combinational multiplier

Barrett方法［2-4］利用模约减运算代替了高成本的除法。如果使用模约减方法直接代替一般的模运算，则需要一种高成本的与模相关的的计算，因此本文中的设计方法适用于对一个模的多次约减运算。

假设Bk-1＜m＜Bk，其中B是基（B通常是2或2的幂）。如果m是B的幂，计算很简单。z=xmodm的值是m整除x所得的余数，也就是

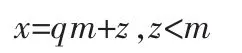
Barrett算法首先计算q=⌊x/m」的近似值q′，因此

首先计算（随后计算q的近似值q′）

因为z=x-qm，由式（2）和式（3）得

令t为使

的最小整数，则

故

又由式（3）得出

下面的算法用于计算（k+T）比特数r=xmodm，其中包括计算q=⌊x/m」的近似值q′的approximation函数。

算法2.1 n-digit to（k+t）-digit约减

q:=approximation（x，m）；//q=⌊x/m」的近似值q′

r:=（（x mod Bk+t）-（q*m mod Bk+t））mod Bk+t；//计算 （k+T）比特数r=xmodm

如果a=2且B≥3，则式（5）中Bt≥3且t=1时等式成立。因而，可用modBk+1来计算x-q′m，该情况与经典的Barrett算法相对应。

下面我们给出计算q的近似值q′的一种方法［5］。

把x和m用基B表示为

q=⌊x/m」的近似值q′是

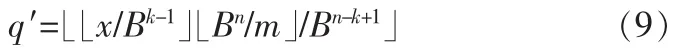
可以看到

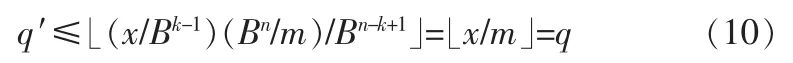
此外

又因x＜Bn且m≥Bk-1则

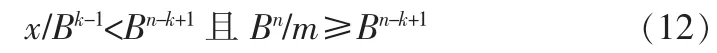
于是

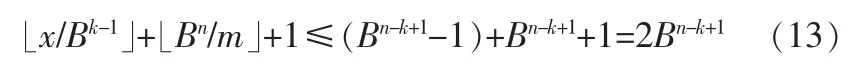
由式（11）和式（12）得出

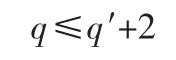
相当于

根据式（5）和式（14），t的值要符合Bt≥3，因此

若B=2，则t=2（估算时运算modBk+2），

若B＞2，则t=1（估算时运算modBk+1）。

综上总结，可得出计算z=xmodp的算法2.2，其中，常数c必需提前计算，如式（15）。

图2 Barrett约减算法的数据路径（B=2）Fig.2 Datapath of a Barrett reducer

B=2时Barrett约减的数据路径对应图2所示。图中乘法器的输入值mul1与mul2的大小取决于n与k的相对值：y 和c是（n-k+1）-bit数，q是（k+2）-bit数，m是k-bit数，因此

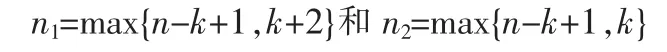
所述时钟信号的最小周期值是n1-bit×n2-bit乘法器的延迟，上述乘法器仅使用了（n+3）个输出。若使用进位保留乘法器，则相应消耗时间约为（n+3）TMULT。由式（6）和式（14），且r′＜3m，则得出最终计算结果为r′，r′-m或r′-2m。因此，总的计算时间最多是5个周期，则

3 基于Stratix II器件的硬件实现

Stratix II器件是Altera在2004年初推出的采用1.2 V、90 nm、9层金属走线、全铜SRAM工艺制造的高端FPGA［6］，它的内部主要特性有内嵌RAM模块、DSP块、锁相环（PLL）和外部的存储器接口等，同时采用了全新的逻辑结构——自适应逻辑模块（Adaptive Logic Module，ALM），在降低了成本的基础上显著地提高了性能和逻辑利用率。

文中基于StratixII系列器件EP2S180F1508C3芯片，以Quartus II 9.0为开发环境，采用硬件描述语言VHDL进行进位保留Barrett模乘法器的FPGA设计与实现，并对实现结果分析验证。

4 进位保留Barrett模乘法器的设计

进位保留Barrett模乘法器，即乘法部分使用进位保留乘法器，求模运算部分使用 Barrett约减运算。电路如图 3所示。

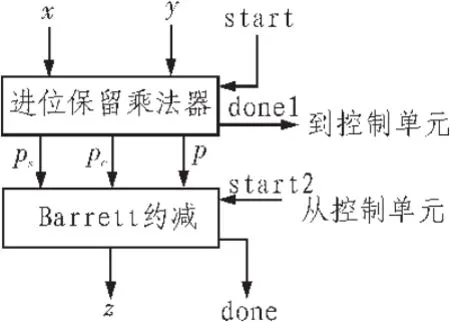
图3 Barrett模乘法器Fig.3 Carry-save Barrett modular multiplication

如图3中的第一个模块是进位保留乘法器，第二个模块是2节中的Barrett模约减电路，总的计算时间是计算两个模块所用时间的总和。

图4 进位保留Barrett模乘法器接口定义Fig.4 Carry-save Barrett modular multiplication's block symbol files

图3的接口定义如图4所示。实现结果基于模齿为p192。

本文取模数：

m=p192=2192-264-1=（FFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFEFFFFFFFFFFFFFFFF）16。仿真结果得出：共使用7 132个组合ALUTs，589个专用逻辑寄存器，仿真结果如图5所示。

图5 Barrett模乘法器仿真结果Fig.5 Carry-save Barrett modular multiplication’s simulation results

编译和仿真后得到Barrett模乘法器的运行最高频率为260.76 MHz，运行的总时钟数为186，数据宽度为192 bit。根据公式：速度=最高频率 （主频）*数据宽度/运行总时钟数（bit/s），经过计算得出运行速度：

260.76 MHz/186*192bit=269.17 Mb/s

表1为与已设计出的模乘法器的性能比较。

表1 性能比较Tab.1 Performance comparison

经过对比，可以看出本文设计出的模乘法器各方面综合性能较佳。

图 3中，x=（13579BDF）16，y=（2468ACE）16，计算出 z= （2C03A9277FA372）16，与仿真结果一致，则结果正确。改变模数m及被求模的数x，仍可验证仿真结果的正确性。

5 结束语

本文应用 VHDL语言，利用进位保留乘法器及Barrett约减运算，设计出Barrett模乘法器，并在QuartusⅡ9.0环境下进行了综合仿真验证，结果与理论一致，验证其正确性。这种方法能够充分发挥硬件的速度和并行性，计算速率可以达到269.17 Mb/s，相比于Barrett算法［8］中的预计算部分使用的除法算法，在Barrett模乘法器只用到乘法算法及模约减运算，大大降低了设计复杂度以及硬件成本，运算效率提高，在公钥密码体制领域应用前景广阔。

［1］张远洋.素数域上公钥密码加速器库的研究与实现［D］.郑州：解放军信息工程大学，2007.

［2］Jean-Pierre Deschamps，José Luis Ima？a，Gustavo D.Sutter，et al.Hardware Implementation of Finite-Field Arithmetic ［M］.3rd ed.［S.l.］:The McGraw-Hill Companies，2009.

［3］Parhami B.Computer Arithmetic［M］.New York:Oxford University Press，2000.

［4］Ercegovac M D，Lang T.Digital Arithmetic［M］.San Francisco: Morgan Kaufmann，2004.

［5］J.-P.Deschamps，G.Bioul，G.Sutter，et al.Synthesis of Arithmetic Circuits［M］.Wiley，Hoboken，New Jersey:Wiley，Hoboken，2006.

［6］葛亚明，彭永丰，薛冰，等.零基础学FPGA［M］.北京：机械工业出版社，2010.

［7］TENCA A F，TODOROV GKOC C K.High-radix Design of a Scalable Modular Multiplier［A］.Cryptography Hardware and Embedded System-CHES 2001.Springer Verlag，Berlin，Gcrmanv，2001：189-205.

［8］Barrett P.Implementing the Rivest，Shamir and Adleman Public-key Encryption Algorithm on Standard Digital Signal Processor［C］.In:Cryptology-CRYPTO’86 Proceedings，vol.263 of Lecture Notes in Computer Science，Springer-Verlag，1987:311-323.

FPGA design and implementation of the carry-save Barrett modular multiplication

CHE Wen-jie，GAO Xian-wei
（Beijing Electronic Science and Technology Institute，Beijing 100070，China）

modulo arithmetic operation of multiplication on prime field is the most basic and most time-consuming operation，therefore，It is very important to design the faster operation speed，less resource efficient multiplier，This paper design a carry-save Barrett modular multiplier，multiplication part use carry-save multiplier，the modulo operation part use Barrett subtraction operation，It's designed and implemented on FPGA by hardware description language and the implementation results are verified.The Barrett modular multiplication operation requires approximately 186 clock cycles and the calculated rate can reach 269.17Mb/s for 192 bit operand.

Barrett modulo subtraction algorithm；Barrett modular multiplication；Field Programmable Gate Array；hardware description language

TN918.2

A

1674－6236（2016）04-0007-03

2015-03-03 稿件编号：201503048

北京市教育教学改革项目（121）；北京电子科技学院教研基金项目（jy201218）

车文洁（1991—），女，甘肃天水人，硕士研究生。研究方向：密码算法的硬件实现等。