例析立体几何问题的优化策略

☉江苏省扬中市第二高级中学 朱卫红

例析立体几何问题的优化策略

☉江苏省扬中市第二高级中学 朱卫红

立体几何是每年高考的必考科目，难度中等.在学习立体几何知识的过程中，如果能够灵活地运用所学的知识，开动脑筋，拓展四维解题空间，常常可以寻觅到巧妙的解法，既可以简化解题过程，还可以降低解题难度，收到事半功倍的效果.本文通过平时的教学实践谈谈如何优化立体几何问题.

策略一、通过向平面作射影，达到降维的目的

在求解立体几何问题时，经常通过射影、平移转化为平面几何知识解决.

例1 如图1，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC=∠BAD=，PA=AD=2，AB= BC=1.

图1

（Ⅰ）求平面PAB与平面PCD所成二面角的余弦值；

（Ⅱ）点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线段BQ的长.

此题最容易想到利用空间坐标系解决，也能最快实施的一种好方法，但要想在尽可能短的时间里高效地解答出结果，对题目条件的有效挖掘就显得尤为重要，同时从高三复习对题目使用的有效性角度看，也很有必要将所学的知识点深度挖掘.对于求二面角的相关问题，方法主要有：定义法，垂面法，三垂线定理法，射影面积法，补棱法，补形法等.下面就射影面积法简答如下：内的射影为△PAB.

设平面PAB与平面PCD所成的锐二面角为θ，

点评：转化为已经学习的平面几何知识解题，会事半功倍.省去了对函数的琐碎研究，而此法的形成无疑是对题目条件的有效利用，对转化与化归思想解题功能的最佳解读，更是对高考“多思少算”理念的完美阐释.

策略二、善于补形和分割，达到优化图形的目的

立体几何题中涉及的图可能是由几个基本图形拼凑出来，有时也可以分割成几个简单图形，因此期间的解题方法也可以迁移运用.涉及的基本方法就是通过分割和补形来构建基本图形.基于此考虑，上例1也可以通过补棱后利用三垂线关系造角：

解：如图2，延长AB，DC交于点R，连接PR，故平面PAB与平面PCD的交线为PR，取PR的中点T，连接AT，DT. PR⇒∠ATD是平面PCD与平面PAB所成的锐二面角.

图2

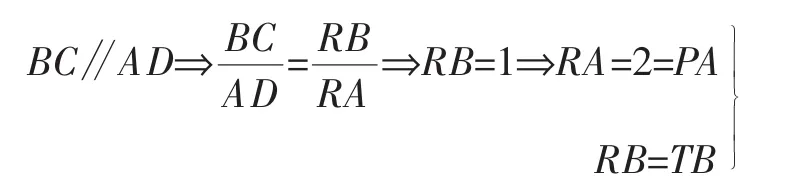
例2 如图3，三棱锥P-ABC中，已知PA⊥BC，PA=BC=l，PA、BC的公垂线ED= h，求三棱锥P-ABC的体积.

解析：连∠BE、EC.

因为PA⊥BC，PA⊥ED且BC∩ED= D，所以PA⊥平面BEC.

图3

因为S△BEC=

所以VA-BEC=lh·PE=lh·AE，

VP-BEC=

VP-ABC=VA-BEC+VP-BEC=

点评：在解决体积问题时，分割和补形是常用的手段与方法，可以将复杂不规则的图形补成熟悉的几何体，从而快速找到解决问题的办法.

策略三、通过体积的不变性设而不求

运用“算两次”的思想，将同一个问题从两个不同的角度来计算，建立相应的等量关系.

例3 如图4，在四面体ABCD中，AB= a，AB=b，AB与CD所成的角θ为何值时，该四面体体积V有最大值？这个最大值是多少？

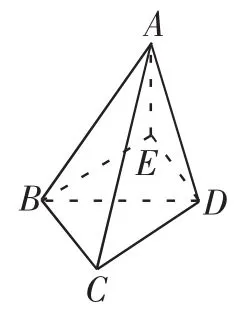
图4

解：AB与CD是异面直线，这就造成了条件的离散，给问题的解决带来了不小的困难.若注意到异面直线所成的角的定义，过B作BE∥CD，并使BE=CD，那么∠ABE=θ，这样在△ABE中就聚集了大部分的已知条件.再由CD∥面ABE，知D到平面ABE的距离，就是AB与CD的距离d.因此有V=VA-BCD=VA-BDE=

因而当θ=90°，即当对棱AB与CD垂直时，四面体体积最大，其体积的最大值为

例4 ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GB垂直于正方形ABCD所在的平面，且GC=2，求点B到平面EFG的距离.

解：如图5，取EF的中点O，连接GB、GO、CD、FB，构造三棱锥BEFG.

图5

点评：等积法不直接求解，而是作为中间过渡，即设而不求，巧妙地将复杂的运算简化，这种方法在解决与圆锥曲线的弦的中点等多种问题时非常奏效.

策略四、充分利用空间向量，达到以算代证的目的

纵观近年来高考立体几何试题标准答案基本都是一题两法即综合法和坐标向量法，利用坐标向量法解决立体几何问题是种普遍、行之有效的方法，把空间几何问题转化为纯代数运算，避免了繁琐的推理论证过程，也大大降低了对学生空间想象能力的要求，为解决立体几何问题的开辟一条新的思路.

通过中国知网等数据库检索发现，对体育舞蹈协调性与灵敏素质的相关研究仅有11篇，且大多是以体育、舞蹈专业院校学生为调查对象，以普通大学生为调查对象的实验研究较少。

例5 如图6，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2.

图6

（Ⅰ）证明：AP⊥BC.

（Ⅱ）在线段AP上是否存在点M，使得二面角A-MC-β为直二面角？若存在，求出AM的长；若不存在，请说明理由.

解法1（构图）：（Ⅰ）证明：所以∴AD⊥BC，又PO⊥平面ABC，所以∴PO⊥BC.

因为∵PO∩AD=O，所以BC⊥平面PAD，所以BC⊥PA.

（Ⅱ）如图7，在平面PAB内作BM⊥AP于M，连接CM，

由（Ⅰ）知BC⊥PA，得PA⊥平面BMC，又AP⊂平面PAC，所以平面BMC⊥平面PAC.

在Rt△ADB中，AB2=AD2+BD2=41得AB=

在Rt△POD中，PD2=PO2+OD2，

在Rt△POA中，PA2=AO2+OP2=25，得PA=5，又cos∠BPA=

图7

所以PM=PBcos∠BPA=2，所以AM=PA-PM=3，所以存在点M符合题意，AM=3.

解法2（向量法）：（Ⅰ）证明：如图，以O为原点，以射线OP为x轴的正半轴，建立空间直角坐标系o-xyz，则O （0，0，0），A（0，-3，0），B（4，2，0），C（-4，2，0），P（0，0，4），由此可得，所以，即AP⊥BC

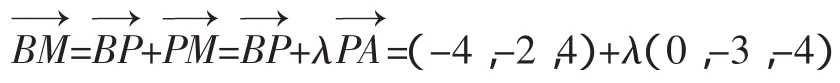
设平面BMC的法向量n1=（x1，y1，z1），平面APC的法向量n2=（x2，y2，z2）

1同理由得可取n2=（5，4，-3），由n1·n2=0，得4-3·=0，解得λ=，故AM=3.

综上所述，存在点M符合题意，AM=3.

点评：用几何法需作辅助线，构造转化为平面问题，解三角形或四边形；用坐标向量法关键在于坐标系的建立，并求对一些点的坐标.同一道题多问中可采用不同的方法，直观简洁，省时省力，不拘一格，问题易得到解决就是好方法.